Abstract
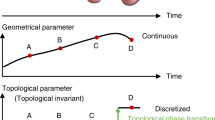
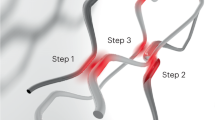
The application of topology, the mathematics of conserved properties under continuous deformations, is creating a range of new opportunities throughout photonics. This field was inspired by the discovery of topological insulators, in which interfacial electrons transport without dissipation, even in the presence of impurities. Similarly, the use of carefully designed wavevector-space topologies allows the creation of interfaces that support new states of light with useful and interesting properties. In particular, this suggests unidirectional waveguides that allow light to flow around large imperfections without back-reflection. This Review explains the underlying principles and highlights how topological effects can be realized in photonic crystals, coupled resonators, metamaterials and quasicrystals.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Haldane, F. D. M. Model for a quantum Hall effect without landau levels: Condensed-matter realization of the 'parity anomaly'. Phys. Rev. Lett. 61, 2015–2018 (1988).
Haldane, F. D. M. & Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904 (2008).
Raghu, S. & Haldane, F. D. M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 78, 033834 (2008).
Joannopoulos, J. D., Johnson, S. G., Winn, J. N. & Meade, R. D. Photonic Crystals: Molding the Flow of Light 2nd edn (Princeton Univ. Press, 2008).
Wang, Z., Chong, Y. D., Joannopoulos, J. D. & Marin Soljačić. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 100, 013905 (2008).
Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljačić., M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).
Hafezi, M., Demler, E. A., Lukin, M. D. & Taylor, J. M. Robust optical delay lines with topological protection. Nature Phys. 7, 907–912 (2011).
Fang, K., Yu, Z. & Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nature Photon. 6, 782–787 (2012).
Khanikaev, A. B. et al. Photonic topological insulators. Nature Mater. 12, 233–239 (2013).
Lu, L., Fu, L., Joannopoulos, J. D. & Soljačić, M. Weyl points and line nodes in gyroid photonic crystals. Nature Photon. 7, 294–299 (2013).
Skirlo, S. A., Lu, L. & Soljačić, M. Multimode one-way waveguides of large Chern numbers. Phys. Rev. Lett. 113, 113904 (2014).
Kraus, Y. E., Lahini, Y., Ringel, Z., Verbin, M. & Zilberberg, O. Topological states and adiabatic pumping in quasicrystals. Phys. Rev. Lett. 109, 106402 (2012).
Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).
Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nature Photon. 7, 1001–1005 (2013).
Sepkhanov, R. A., Nilsson, J. & Beenakker, C. W. J. Proposed method for detection of the pseudospin-1/2 Berry phase in a photonic crystal with a Dirac spectrum. Phys. Rev. B 78, 045122 (2008).
Sepkhanov, R. A., Ossipov, A. & Beenakker, C. W. J. Extinction of coherent backscattering by a disordered photonic crystal with a Dirac spectrum. Europhys. Lett. 85, 14005 (2009).
Peleg, O. et al. Conical diffraction and gap solitons in honeycomb photonic lattices. Phys. Rev. Lett. 98, 103901 (2007).
Bahat-Treidel, O. et al. Klein tunneling in deformed honeycomb lattices. Phys. Rev. Lett. 104, 063901 (2010).
Rechtsman, M. C. et al. Strain-induced pseudomagnetic field and photonic landau levels in dielectric structures. Nature Photon. 7, 153–158 (2013).
Schomerus, H. & Halpern, N. Y. Parity anomaly and Landau-level lasing in strained photonic honeycomb lattices. Phys. Rev. Lett. 110, 013903 (2013).
Rechtsman, M. C. et al. Topological creation and destruction of edge states in photonic graphene. Phys. Rev. Lett. 111, 103901 (2013).
Onoda, M., Murakami, S. & Nagaosa, N. Hall effect of light. Phys. Rev. Lett. 93, 083901 (2004).
Ochiai, T. & Onoda, M. Photonic analog of graphene model and its extension: Dirac cone, symmetry, and edge states. Phys. Rev. B 80, 155103 (2009).
Fang, K., Yu, Z. & Fan, S. Microscopic theory of photonic one-way edge mode. Phys. Rev. B 84, 075477 (2011).
Poo, Y., Wu, R.-X., Lin, Z., Yang, Y. & Chan, C. T. Experimental realization of self-guiding unidirectional electromagnetic edge states. Phys. Rev. Lett. 106, 93903 (2011).
Liu, K., Shen, L. & He, S. One-way edge mode in a gyromagnetic photonic crystal slab. Opt. Lett. 37, 4110–4112 (2012).
Asatryan, A. A., Botten, L. C., Fang, K., Fan, S. & McPhedran, R. C. Local density of states of chiral Hall edge states in gyrotropic photonic clusters. Phys. Rev. B 88, 035127 (2013).
He, C. et al. Tunable one-way cross-waveguide splitter based on gyromagnetic photonic crystal. Appl. Phys. Lett. 96, 111111 (2010).
Zang, X. & Jiang, C. Edge mode in nonreciprocal photonic crystal waveguide: manipulating the unidirectional electromagnetic pulse dynamically. J. Opt. Soc. Am. B 28, 554–557 (2011).
Fu, J.-X., Liu, R.-J. & Li, Z.-Y. Robust one-way modes in gyromagnetic photonic crystal waveguides with different interfaces. Appl. Phys. Lett. 97, 041112 (2010).
Fu, J.-X., Lian, J., Liu, R.-J., Gan, L. & Li, Z.-Y. Unidirectional channel-drop filter by one-way gyromagnetic photonic crystal waveguides. Appl. Phys. Lett. 98, 211104 (2011).
Qiu, W., Wang, Z. & Soljačić, M. Broadband circulators based on directional coupling of one-way waveguides. Opt. Express 19, 22248–22257 (2011).
Yang, Y., Poo, Y., Wu, R.-X., Gu, Y. & Chen, P. Experimental demonstration of one-way slow wave in waveguide involving gyromagnetic photonic crystals. Appl. Phys. Lett. 102, 231113 (2013).
Chong, Y. D., Wen, X. G. & Soljačić, M. Effective theory of quadratic degeneracies. Phys. Rev. B 77, 235125 (2008).
Yu, Z., Veronis, G., Wang, Z. & Fan, S. One-way electromagnetic waveguide formed at the interface between a plasmonic metal under a static magnetic field and a photonic crystal. Phys. Rev. Lett. 100, 23902 (2008).
Mittal, S. et al. Topologically robust transport of photons in a synthetic gauge field. Phys. Rev. Lett. 113, 087403 (2014).
Umucalılar, R. O. & Carusotto, I. Artificial gauge field for photons in coupled cavity arrays. Phys. Rev. A 84, 043804 (2011).
Petrescu, A., Houck, A. A. & Le Hur, K. Anomalous Hall effects of light and chiral edge modes on the Kagome lattice. Phys. Rev. A 86, 053804 (2012).
Hafezi, M. Measuring topological invariants in photonic systems. Phys. Rev. Lett. 112, 210405 (2014).
Liang, G. Q. & Chong, Y. D. Optical resonator analog of a two-dimensional topological insulator. Phys. Rev. Lett. 110, 203904 (2013).
Pasek, P. & Chong, Y. D. Network models of photonic Floquet topological insulators. Phys. Rev. B 89, 075113 (2013).
Fang, K., Yu, Z. & Fan, S. Photonic Aharonov–Bohm effect based on dynamic modulation. Phys. Rev. Lett. 108, 153901 (2012).
Li, E., Eggleton, B. J., Fang, K. & Fan, S. Photonic Aharonov–Bohm effect in photon–phonon interactions. Nature Commun. 5, 3225 (2014).
Tzuang, L. D., Fang, K., Nussenzveig, P., Fan, S. & Lipson, M. Non-reciprocal phase shift induced by an effective magnetic flux for light. Nature Photon. 8, 701–705 (2014).
Kitagawa, T., Berg, E., Rudner, M. & Demler, E. Topological characterization of periodically driven quantum systems. Phys. Rev. B 82, 235114 (2010).
Lindner, N. H., Refael, G. & Galitski, V. Floquet topological insulator in semiconductor quantum wells. Nature Phys. 7, 490–495 (2011).
Kopp, V. I. et al. Chiral fiber gratings. Science 305, 74–75 (2004).
Jia, S. & Fleischer, J. W. Nonlinear light propagation in rotating waveguide arrays. Phys. Rev. A 79, 041804 (2009).
Dalibard, J., Gerbier, F., Juzeliūnas, G. & Öhberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 83, 1523 (2011).
Jaksch, D. & Zoller, P. Creation of effective magnetic fields in optical lattices: the Hofstadter butterfly for cold neutral atoms. New J. Phys. 5, 56 (2003).
Schmidt, M., Peano, V. & Marquardt, F. Optomechanical metamaterials: Dirac polaritons, gauge fields, and instabilities. Preprint at http://lanl.arxiv.org/abs/1311.7095 (2013).
Jia, N., Sommer, A., Schuster, D. & Simon, J. Time reversal invariant topologically insulating circuits. Preprint at http://lanl.arxiv.org/abs/1309.0878 (2013).
Kong, J. A. Theorems of bianisotropic media. Proc. IEEE 60, 1036–1046 (1972).
Jonsson, F. & Flytzanis, C. Photospin-orbit coupling in photonic structures. Phys. Rev. Lett. 97, 193903 (2006).
Ma, T., Khanikaev, A. B., Mousavi, S. H. & Shvets, G. Topologically protected photonic transport in bi-anisotropic meta-waveguides. Preprint at http://lanl.arxiv.org/abs/1401.1276 (2014).
Chen, W.-J., Jiang, S.-J., Chen, X.-D., Dong, J.-W. & Chan, C. T. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Preprint at http://lanl.arxiv.org/abs/1401.0367 (2014).
Gao, W. et al. Chiral hyperbolic metamaterial as a robust photonic topological insulator. Preprint at http://lanl.arxiv.org/abs/1401.5448 (2014).
Kraus, Y. E., Ringel, Z. & Zilberberg, O. Four-dimensional quantum Hall effect in a two-dimensional quasicrystal. Phys. Rev. Lett. 111, 226401 (2013).
Chen, W.-J. et al. Observation of backscattering-immune chiral electromagnetic modes without time reversal breaking. Phys. Rev. Lett. 107, 023901 (2011).
Lu, L., Joannopoulos, J. D. & Soljačić, M. Waveguiding at the edge of a three-dimensional photonic crystal. Phys. Rev. Lett. 108, 243901 (2012).
Burkov, A. A., Hook, M. D. & Balents, L. Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011).
Young, S. M. et al. Dirac semimetal in three dimensions. Phys. Rev. Lett. 108, 140405 (2012).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Malkova, N., Hromada, I., Wang, X., Bryant, G. & Chen, Z. Observation of optical Shockley-like surface states in photonic superlattices. Opt. Lett. 34, 1633–1635 (2009).
Tan, W., Sun, Y., Chen, H. & Shen, S.-Q. Photonic simulation of topological excitations in metamaterials. Sci. Rep. 4, 3842 (2014).
Poshakinskiy, A. V., Poddubny, A. N., Pilozzi, L. & Ivchenko, E. L. Radiative topological states in resonant photonic crystals. Phys. Rev. Lett. 112, 107403 (2014).
Xiao, M., Zhang, Z. Q. & Chan, C. T. Surface impedance and bulk band geometric phases in one-dimensional systems. Phys. Rev. X 4, 021017 (2014).
Poddubny, A., Miroshnichenko, A., Slobozhanyuk, A. & Kivshar, Y. Topological Majorana states in zigzag chains of plasmonic nanoparticles. ACS Photon. 1, 101–105 (2014).
Ling, C. W., Xiao, M., Yu, S. F. & Fung, K. H. Topological edge plasmon modes between diatomic chains of nanoparticles. Preprint at http://lanl.arxiv.org/abs/1401.7520 (2014).
Poli, C., Bellec, M., Kuhl, U., Mortessagne, F. & Schomerus, H. Selective enhancement of topologically induced interface states. Preprint at http://lanl.arxiv.org/abs/1407.3703 (2014).
Kitaev, A. Periodic table for topological insulators and superconductors. AIP Conf. Proc. 1134, 22 (2009).
Schnyder, A. P., Ryu, S., Furusaki, A. & Ludwig, A. W. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Yannopapas, V. Gapless surface states in a lattice of coupled cavities: A photonic analog of topological crystalline insulators. Phys. Rev. B 84, 195126 (2011).
De Nittis, G. & Lein, M. On the role of symmetries in the theory of photonic crystals. Ann. Phys. 350, 568–587 (2014).
Chen, X., Gu, Z.-C., Liu, Z.-X. & Wen, X.-G. Symmetry-protected topological orders in interacting bosonic systems. Science 338, 1604–1606 (2012).
Umucalilar, R. O. & Carusotto, I. Fractional quantum Hall states of photons in an array of dissipative coupled cavities. Phys. Rev. Lett. 108, 206809 (2012).
Hafezi, M., Lukin, M. D. & Taylor, J. M. Non-equilibrium fractional quantum Hall state of light. New J. Phys. 15, 063001 (2013).
Lumer, Y., Plotnik, Y., Rechtsman, M. C. & Segev, M. Self-localized states in photonic topological insulators. Phys. Rev. Lett. 111, 243905 (2013).
Yuen-Zhou, J., Saikin, S. K., Yao, N. Y. & Aspuru-Guzik, A. Topologically protected excitons in porphyrin thin films. Nature Mater. http://dx.doi.org/10.1038/nmat4073 (2014).
Jacqmin, T. et al. Direct observation of Dirac cones and a flatband in a honeycomb lattice for polaritons. Phys. Rev. Lett. 112, 116402 (2014).
Karzig, T., Bardyn, C.-E., Lindner, N. & Refael, G. Topological polaritons from quantum wells in photonic waveguides or microcavities. Preprint at http://lanl.arxiv.org/abs/1406.4156 (2014).
Prodan, E. & Prodan, C. Topological phonon modes and their role in dynamic instability of microtubules. Phys. Rev. Lett. 103, 248101 (2009).
Kane, C. L. & Lubensky, T. C. Topological boundary modes in isostatic lattices. Nature Phys. 10, 39–45 (2013).
Shindou, R., Matsumoto, R. & Murakami, S. Topological chiral magnonic edge mode in a magnonic crystal. Phys. Rev. B 87, 174427 (2013).
Zhen, B., Hsu, C. W., Lu, L., Stone, A. D. & Soljačić, M. Topological nature of bound states in the radiation continuum. Preprint at http://lanl.arxiv.org/abs/1408.0237 (2014).
Koch, J., Houck, A. A., Le Hur, K. & Girvin, S. M. Time-reversal-symmetry breaking in circuit-QED-based photon lattices. Phys. Rev. A 82, 043811 (2010).
Aspuru-Guzik, A., Demler, E. & White, A. G. Observation of topologically protected bound states in photonic quantum walks. Nature Commun. 3, 882 (2012).
Jalas, D. et al. What is and what is not an optical isolator. Nature Photon. 7, 579–582 (2013).
Nakahara, M. Geometry, topology, and physics (CRC, 2003).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959 (2010).
Fukui, T., Hatsugai, Y. & Suzuki, H. Chern numbers in discretized Brillouin zone: Efficient method of computing (spin) Hall conductances. J. Phys. Soc. Japan 74, 1674–1677 (2005).
Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indiana Acad. Sci. A44, 247–262 (1956).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond A 392, 45–57 (1984).
Tomita, A. & Chiao, R. Y. Observation of Berry's topological phase by use of an optical fiber. Phys. Rev. Lett. 57, 937 (1986).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Acknowledgements
L.L. thanks L. Fu, C. Wang and A. Khanikaev for discussions. The authors thank P. Rebusco and C.W. Hsu for critical reading and editing of the manuscript. J.J. was supported in part by the U.S.A.R.O. through the ISN, under contract W911NF-07-D-0004. L.L. was supported in part by the MRSEC Program of the NSF under award DMR-0819762. M.S. and L.L. were supported in part by the MIT S3TEC EFRC of DOE under grant DE-SC0001299.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Lu, L., Joannopoulos, J. & Soljačić, M. Topological photonics. Nature Photon 8, 821–829 (2014). https://doi.org/10.1038/nphoton.2014.248
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2014.248
This article is cited by
-
Nonlinear topological symmetry protection in a dissipative system
Nature Communications (2024)
-
Nonlinearity-induced topological phase transition characterized by the nonlinear Chern number
Nature Physics (2024)
-
Non-Hermitian topological phase transitions controlled by nonlinearity
Nature Physics (2024)
-
Linear and phase controllable terahertz frequency conversion via ultrafast breaking the bond of a meta-molecule
Nature Communications (2024)
-
Topological single-photon emission from quantum emitter chains
npj Quantum Information (2024)