Abstract
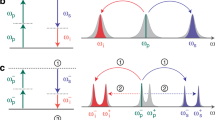
It is widely accepted that information cannot travel faster than c, the speed of light in vacuum1,2,3. Here, we investigate the behaviour of quantum correlations and information in the presence of dispersion. To do so we send one half of an entangled state of light through a gain-assisted slow- or fast-light medium and detect the transmitted quantum correlations and quantum mutual information4,5,6. We show that quantum correlations can be advanced by a small fraction of the correlation time, even in the presence of noise added by phase-insensitive gain. Additionally, although the peak of the quantum mutual information between the modes can be advanced, we find that the degradation of the mutual information due to added noise appears to prevent an advancement of the leading edge. In contrast, we demonstrate a significant delay of both the leading and trailing edges of the mutual information in a slow-light system.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Garrison, J. C., Mitchell, M. W., Chiao, R. Y. & Bolda, E. L. Superluminal signals: causal loop paradoxes revisited. Phys. Lett. A 245, 19–25 (1998).
Milonni, P. W. Fast Light, Slow Light and Left-handed Light (Taylor & Francis, 2010).
Boyd, R. W. Slow and fast light: fundamentals and applications. J. Mod. Opt. 56, 1908–1915 (2009).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Braunstein, S. L. & van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 77, 513–577 (2005).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621–669 (2012).
Glasser, R. T., Vogl, U. & Lett, P. D. Stimulated generation of superluminal light pulses via four-wave mixing. Phys. Rev. Lett. 108, 173902 (2012).
Camacho, R. M., Pack, M. V., Howell, J. C., Schweinsberg, A. & Boyd, R. W. Wide-bandwidth, tunable, multiple-pulse-width optical delays using slow light in cesium vapor. Phys. Rev. Lett. 98, 153601 (2007).
Hau, L. V., Harris, S. E., Dutton, Z. & Behroozi, C. H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 397, 594–598 (1999).
Glasser, R. T., Vogl, U. & Lett, P. D. Demonstration of images with negative group velocities. Opt. Express 20, 13702–13710 (2012).
Keaveney, J., Hughes, I. G., Sargsyan, A., Sarkisyan, D. & Adams, C. S. Maximal refraction and superluminal propagation in a gaseous nanolayer. Phys. Rev. Lett. 109, 233001 (2012).
Brillouin, L. Über die Fortpflanzung des Lichtes in dispergierenden Medien. Ann. Phys. (Leipz.) 349, 203–240 (1914).
Sommerfeld, A. Ein Einwand gegen die Relativtheorie der Elektrodynamik und seine Beseitigung. Phys. Zeit. 8, 841–842 (1907).
Chiao, R. Y. & Steinberg, A. M. in Progress in Optics Vol. 37 (ed. Wolf, E.) 345–405 (Elsevier, 1997).
Stenner, M. D., Gauthier, D. J. & Neifeld, M. A. The speed of information in a ‘fast-light’ optical medium. Nature 425, 695–698 (2003).
Kuzmich, A., Dogariu, A., Wang, L. J., Milonni, P. W. & Chiao, R. Y. Signal velocity, causality, and quantum noise in superluminal light pulse propagation. Phys. Rev. Lett. 86, 3925–3929 (2001).
Boyer, V., Marino, A. M., Pooser, R. C. & Lett, P. D. Entangled images from four-wave mixing. Science 321, 544–547 (2008).
Peres, A. & Terno, D. R. Quantum information and relativity theory. Rev. Mod. Phys. 76, 93–123 (2004).
Lvovsky, A. I., Sanders, B. C. & Tittel, W. Optical quantum memory. Nature Photon. 3, 706–714 (2009).
Marino, A. M., Pooser, R. C., Boyer, V. & Lett, P. D. Tunable delay of Einstein–Podolsky–Rosen entanglement. Nature 457, 859–862 (2009).
Hutchings, D. C., Sheik-Bahae, M., Hagan, D. & Stryland, E. Kramers–Krönig relations in nonlinear optics. Opt. Quantum Electron. 24, 1–30 (1992).
Duan, L.-M., Giedke, G., Cirac, J. I. & Zoller, P. Inseparability criterion for continuous variable systems. Phys. Rev. Lett. 84, 2722–2725 (2000).
Vogl, U. et al. Advanced quantum noise correlations. New J. Phys. 16, 013011 (2014).
Caves, C. M. Quantum limits on noise in linear amplifiers. Phys. Rev. D. 26, 1817–1839 (1982).
Boyd, R. W., Shi, Z. & Milonni, P. W. Noise properties of propagation through slow- and fast-light media. J. Opt. 12, 104007 (2010).
Ollivier, H. & Zurek, W. H. Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001).
Stenner, M. D., Gauthier, D. J. & Neifeld, M. A. Fast causal information transmission in a medium with a slow group velocity. Phys. Rev. Lett. 94, 053902 (2005).
Serafini, A., Illuminati, F. & De Siena, S. Symplectic invariants, entropic measures and correlations of Gaussian states. J. Phys. B 37, L21–L28 (2004).
Vogl, U. et al. Experimental characterization of Gaussian quantum discord generated by four-wave mixing. Phys. Rev. A 87, 010101 (2013).
Acknowledgements
This research was supported by the Physics Frontiers Center at the Joint Quantum Institute and the Air Force Office of Scientific Research. Q.G. performed this work with the support of the Marie Curie IOF FP7 Program (Multimem–300632), while U.V. was supported by the Alexander von Humboldt Foundation and R.T.G. was supported by a National Research Council Research Associateship Award at NIST. J.B.C. acknowledges support from the National Science Foundation.
Author information
Authors and Affiliations
Contributions
J.B.C., R.T.G., Q.G. and U.V. analysed the data. J.B.C., R.T.G., U.V. and P.D.L. conceived and designed the experiments. J.B.C., R.T.G., Q.G. and U.V. contributed materials and analysis tools. J.B.C., R.T.G., Q.G., U.V. and T.L. performed the experiments. J.B.C., R.T.G., Q.G., U.V., K.M.J. and P.D.L. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 829 kb)
Rights and permissions
About this article
Cite this article
Clark, J., Glasser, R., Glorieux, Q. et al. Quantum mutual information of an entangled state propagating through a fast-light medium. Nature Photon 8, 515–519 (2014). https://doi.org/10.1038/nphoton.2014.112
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2014.112
This article is cited by
-
Characterization of Pairwise Correlations from Multiple Quantum Correlated Beams Generated from Cascaded Four-Wave Mixing Processes
Scientific Reports (2017)
-
Quantum optical devices based on four-wave mixing in hot rubidium vapor
Science China Physics, Mechanics & Astronomy (2015)