Abstract
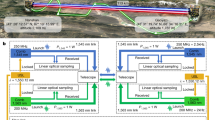
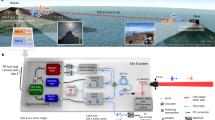
The transfer of high-quality time–frequency signals between remote locations underpins many applications, including precision navigation and timing, clock-based geodesy, long-baseline interferometry, coherent radar arrays, tests of general relativity and fundamental constants, and future redefinition of the second1,2,3,4,5,6,7. However, present microwave-based time–frequency transfer8,9,10 is inadequate for state-of-the-art optical clocks and oscillators1,11,12,13,14,15,16 that have femtosecond-level timing jitter and accuracies below 1 × 10−17. Commensurate optically based transfer methods are therefore needed. Here we demonstrate optical time–frequency transfer over free space via two-way exchange between coherent frequency combs, each phase-locked to the local optical oscillator. We achieve 1 fs timing deviation, residual instability below 1 × 10−18 at 1,000 s and systematic offsets below 4 × 10−19, despite frequent signal fading due to atmospheric turbulence or obstructions across the 2 km link. This free-space transfer can enable terrestrial links to support clock-based geodesy. Combined with satellite-based optical communications, it provides a path towards global-scale geodesy, high-accuracy time–frequency distribution and satellite-based relativity experiments.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Chou, C. W., Hume, D. B., Rosenband, T. & Wineland, D. J. Optical clocks and relativity. Science 329, 1630–1633 (2010).
Bondarescu, R. et al. Geophysical applicability of atomic clocks: direct continental geoid mapping. Geophys. J. Int. 191, 78–82 (2012).
Müller, J., Soffel, M. & Klioner, S. Geodesy and relativity. J. Geod. 82, 133–145 (2008).
Schiller, S. et al. Einstein gravity explorer—a medium-class fundamental physics mission. Exp. Astron. 23, 573–610 (2009).
Wolf, P. et al. Quantum physics exploring gravity in the outer solar system: the SAGAS project. Exp. Astron. 23, 651–687 (2009).
Uzan, J. The fundamental constants and their variation: observational and theoretical status. Rev. Mod. Phys. 75, 403–455 (2003).
Gill, P. When should we change the definition of the second? Phil. Trans. R. Soc. A 369, 4109–4130 (2011).
Bauch, A. et al. Comparison between frequency standards in Europe and the USA at the 10−15 uncertainty level. Metrologia 43, 109–120 (2006).
Samain, E. et al. The T2L2 ground experiment time transfer in the picosecond range over a few kilometres. Proceedings of the 20th European Frequency and Time Forum 538–544 (2006).
Cacciapuoti, L. & Salomon, C. Space clocks and fundamental tests: the ACES experiment. Eur. Phys. J. Special Topics 172, 57–68 (2009).
Chou, C. W., Hume, D. B., Koelemeij, J. C. J., Wineland, D. J. & Rosenband, T. Frequency comparison of two high-accuracy Al+ optical clocks. Phys. Rev. Lett. 104, 070802 (2010).
Katori, H. Optical lattice clocks and quantum metrology. Nature Photon. 5, 203–210 (2011).
Ludlow, A. D. et al. Sr lattice clock at 1 × 10−16 fractional uncertainty by remote optical evaluation with a Ca clock. Science 319, 1805–1808 (2008).
Fortier, T. M. et al. Generation of ultrastable microwaves via optical frequency division. Nature Photon. 5, 425–429 (2011).
Jiang, Y. Y. et al. Making optical atomic clocks more stable with 10−16-level laser stabilization. Nature Photon. 5, 158–161 (2011).
Yamaguchi, A. et al. Direct comparison of distant optical lattice clocks at the 10−16 uncertainty. Appl. Phys. Express 4, 082203 (2011).
Predehl, K. et al. A 920-kilometer optical fiber link for frequency metrology at the 19th decimal place. Science 336, 441–444 (2012).
Lopez, O. et al. Simultaneous remote transfer of accurate timing and optical frequency over a public fiber network. Appl. Phys. B 110, 3–6 (2013).
Sprenger, B., Zhang, J., Lu, Z. H. & Wang, L. J. Atmospheric transfer of optical and radio frequency clock signals. Opt. Lett. 34, 965–967 (2009).
Djerroud, K. et al. Coherent optical link through the turbulent atmosphere. Opt. Lett. 35, 1479–1481 (2010).
Andrews, L. C. & Phillips, R. L. Laser Beam Propagation through Random Media (SPIE Press, 1998).
Coddington, I., Swann, W. C., Nenadovic, L. & Newbury, N. R. Rapid and precise absolute distance measurements at long range. Nature Photon. 3, 351–356 (2009).
Kim, J., Cox, J. A., Chen, J. & Kärtner, F. X. Drift-free femtosecond timing synchronization of remote optical and microwave sources. Nature Photon. 2, 733–736 (2008).
Lee, J., Kim, Y. J., Lee, K., Lee, S. & Kim, S. W. Time-of-flight measurement with femtosecond light pulses. Nature Photon. 4, 716–720 (2010).
Shapiro, J. H. Reciprocity of the turbulent atmosphere. J. Opt. Soc. Am. 61, 492–495 (1971).
Parenti, R. R., Michael, S., Roth, J. M. & Yarnall, T. M. Comparisons of Cn2 measurements and power-in-fiber data from two long-path free-space optical communication experiments. Proc. SPIE 7814, 78140Z (2010).
Marra, G. et al. High-resolution microwave frequency transfer over an 86-km-long optical fiber network using a mode-locked laser. Opt. Lett. 36, 511–513 (2011).
Roy, J., Deschênes, J-D., Potvin, S. & Genest, J. Continuous real-time correction and averaging for frequency comb interferometry. Opt. Express 20, 21932–21939 (2012).
Giorgetta, F. R. et al. in CLEO: Applications and Technology CTh5D.10 (Optical Society of America, 2012).
Conan, J., Rousset, G. & Madec, P-Y. Wave-front temporal spectra in high-resolution imaging through turbulence. J. Opt. Soc. Am. A 12, 1559–1570 (1995).
Koishi, Y. et al. in International Conference on Space Optical Systems and Applications (ICSOS) 88–92 (IEEE, 2011).
Acknowledgements
This work was funded by the Defense Advanced Research Projects Agency (DARPA) QuASAR program and by the National Institute of Standards and Technology (NIST). The authors acknowledge helpful discussions with S. Diddams, J.-D. Deschênes, S. Kaushik, S. Michael, R. Parenti, T. Parker, F. Quinlan and T. Rosenband, and assistance from E. Williams and A. Zolot.
Author information
Authors and Affiliations
Contributions
W.C.S., L.C.S., I.C., E.B., F.R.G. and N.R.N. set up and operated the measurement system. F.R.G. and N.R.N. analysed the TWTF data. L.C.S. and N.R.N. analysed the turbulence data. N.R.N., F.R.G., L.C.S., W.C.S., E.B. and I.C. prepared the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1253 kb)
Rights and permissions
About this article
Cite this article
Giorgetta, F., Swann, W., Sinclair, L. et al. Optical two-way time and frequency transfer over free space. Nature Photon 7, 434–438 (2013). https://doi.org/10.1038/nphoton.2013.69
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2013.69
This article is cited by
-
Quantum-limited optical time transfer for future geosynchronous links
Nature (2023)
-
Frequency comb-to-comb stabilization over a 1.3-km free-space atmospheric optical link
Light: Science & Applications (2022)
-
Dual chirped microcomb based parallel ranging at megapixel-line rates
Nature Communications (2022)
-
The time-programmable frequency comb and its use in quantum-limited ranging
Nature (2022)
-
Optical crosslinks and satellite synchronization for GNSS, communications, and beyond
GPS Solutions (2022)