Abstract
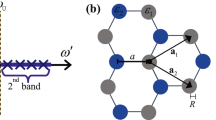
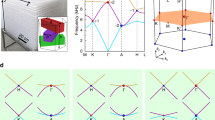
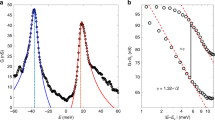
Weyl points and line nodes are three-dimensional linear point and line degeneracies between two bands. In contrast to two-dimensional Dirac points, which are their lower-dimensional analogues, Weyl points are stable in momentum space, and the associated surface states are predicted to be topologically non-trivial. However, Weyl points are yet to be discovered in nature. Here, we report photonic crystals based on double-gyroid structures, exhibiting frequency-isolated Weyl points with complete phase diagrams by breaking the parity and time-reversal symmetries. Gapless surface dispersions associated with non-zero Chern numbers are demonstrated. Line nodes are also found in similar geometries, the associated surface states forming flat dispersion bands. Our results are based on realistic ab initio calculations with true predictive power and should be readily realizable experimentally from microwave to optical frequencies.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009).
Bonaccorso, F., Sun, Z., Hasan, T. & Ferrari, A. C. Graphene photonics and optoelectronics. Nature Photon. 4, 611–622 (2010).
Sepkhanov, R. A., Bazaliy, Y. B. & Beenakker, C. W. J. Extremal transmission at the Dirac point of a photonic band structure. Phys. Rev. A 75, 063813 (2007).
Zhang, X. Observing Zitterbewegung for photons near the Dirac point of a two-dimensional photonic crystal. Phys. Rev. Lett. 100, 113903 (2008).
Peleg, O. et al. Conical diffraction and gap solitons in honeycomb photonic lattices. Phys. Rev. Lett. 98, 103901 (2007).
Bravo-Abad, J., Joannopoulos, J. D. & Soljačić, M. Enabling single-mode behavior over large areas with photonic Dirac cones. Proc. Natl Acad. Sci. USA 109, 9761–9765 (2012).
Rechtsman, M. C. et al. Strain-induced pseudomagnetic field and photonic Landau levels in dielectric structures. Nature Photon. 7, 153–158 (2013).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Haldane, F. D. M. & Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904 (2008).
Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).
Khanikaev, A. B. et al. Photonic topological insulators. Nature Mater. 12, 233–239 (2013).
Rechtsman, M. C. et al. Photonic floquet topological insulators. Preprint at http://lanl.arXiv.org/abs/1212.3146 (2012).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Halász, G. B. & Balents, L. Time-reversal invariant realization of the Weyl semimetal phase. Phys. Rev. B 85, 035103 (2012).
Xu, G., Weng, H., Wang, Z., Dai, X. & Fang, Z. Chern semimetal and the quantized anomalous Hall effect in HgCr2Se4 . Phys. Rev. Lett. 107, 186806 (2011).
Volovik, G. in The Universe in a Helium Droplet Ch. 8 (Clarendon, 2003).
Yang, K-Y., Lu, Y-M. & Ran, Y. Quantum Hall effects in a Weyl semimetal: possible application in pyrochlore iridates. Phys. Rev. B 84, 075129 (2011).
Hosur, P., Parameswaran, S. A. & Vishwanath, A. Charge transport in Weyl semimetals. Phys. Rev. Lett. 108, 046602 (2012).
Aji, V. Adler–Bell–Jackiw anomaly in Weyl semimetals: application to pyrochlore iridates. Phys. Rev. B 85, 241101 (2012).
Schoen, A. Infinite Periodic Minimal Surfaces without Self-intersections, NASA Technical Note No. D-5541 (NASA, 1970).
Wohlgemuth, M., Yufa, N., Hoffman, J. & Thomas, E. L. Triply periodic bicontinuous cubic microdomain morphologies by symmetries. Macromolecules 34, 6083–6089 (2001).
Hahn, T. International Tables for Crystallography (Volume A): Space-group Symmetry Part 7 (Kluwer Academic, 2002).
Mañes, J. L. Existence of bulk chiral fermions and crystal symmetry. Phys. Rev. B 85, 155118 (2012).
Aroyo, M. I., Kirov, A., Capillas, C., Perez-Mato, J. M. & Wondratschek, H. Bilbao crystallographic server. II. Representations of crystallographic point groups and space groups. Acta Crystallogr. A 62, 115–128 (2006).
Maldovan, M., Urbas, A. M., Yufa, N., Carter, W. C. & Thomas, E. L. Photonic properties of bicontinuous cubic microphases. Phys. Rev. B 65, 165123 (2002).
Burkov, A. A., Hook, M. D. & Balents, L. Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011).
Meade, R. D., Brommer, K. D., Rappe, A. M. & Joannopoulos, J. D. Electromagnetic Bloch waves at the surface of a photonic crystal. Phys. Rev. B 44, 10961–10964 (1991).
Bouchaud, J. P. & Zérah, P. G. Spontaneous resonances and universal behavior in ferrimagnets: effective-medium theory. Phys. Rev. Lett. 63, 1000–1003 (1989).
Bernevig, B., Hughes, T., Raghu, S. & Arovas, D. Theory of the three-dimensional quantum Hall effect in graphite. Phys. Rev. Lett. 99, 146804 (2007).
Raghu, S. & Haldane, F. D. M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 78, 033834 (2008).
Wang, Z., Chong, Y. D., Joannopoulos, J. D. & Soljačić, M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 100, 013905 (2008).
Pouya, C. & Vukusic, P. Electromagnetic characterization of millimetre-scale replicas of the gyroid photonic crystal found in the butterfly parides sesostris. Interface Focus 2, 645–650 (2012).
Özbay, E. et al. Measurement of a three-dimensional photonic band gap in a crystal structure made of dielectric rods. Phys. Rev. B 50, 1945–1948 (1994).
Saba, M. et al. Circular dichroism in biological photonic crystals and cubic chiral nets. Phys. Rev. Lett. 106, 103902 (2011).
Hyde, S., Andersson, S., Ericsson, B. & Larsson, K. A cubic structure consisting of a lipid bilayer forming an infinite periodic minimum surface of the gyroid type in the glycerolmonooleat-water system. Z. Kristallogr. 168, 213–219 (1984).
Kresge, C., Leonowicz, M., Roth, W., Vartuli, J. & Beck, J. Ordered mesoporous molecular sieves synthesized by a liquid-crystal template mechanism. Nature 359, 710–712 (1992).
Saranathan, V. et al. Structure, function, and self-assembly of single network gyroid (I4132) photonic crystals in butterfly wing scales. Proc. Natl Acad. Sci. USA 107, 11676–11681 (2010).
Hur, K. et al. Three-dimensionally isotropic negative refractive index materials from block copolymer self-assembled chiral gyroid networks. Angew. Chem. 123, 12191–12195 (2011).
Armatas, G. S. & Kanatzidis, M. G. Mesostructured germanium with cubic pore symmetry. Nature 441, 1122–1125 (2006).
García-Santamara, F. et al. A germanium inverse woodpile structure with a large photonic band gap. Adv. Mater. 19, 1567–1570 (2007).
Ullal, C. K. et al. Triply periodic bicontinuous structures through interference lithography: a level-set approach. J. Opt. Soc. Am. A 20, 948–954 (2003).
Turner, M., Schröder-Turk, G. & Gu, M. Fabrication and characterization of three-dimensional biomimetic chiral composites. Opt. Express 19, 10001–10008 (2011).
Yablonovitch, E., Gmitter, T. J. & Leung, K. M. Photonic band structure: the face-centered-cubic case employing nonspherical atoms. Phys. Rev. Lett. 67, 2295–2298 (1991).
Takahashi, S. et al. Direct creation of three-dimensional photonic crystals by a top-down approach. Nature Mater. 8, 721–725 (2009).
Lu, L. et al. Three-dimensional photonic crystals by large-area membrane stacking. Opt. Lett. 37, 4726–4728 (2012).
Acknowledgements
The authors thank F. Wang, M. Maldovan, Y. Ran, Z. Wang, S. G. Johnson, A. Vishwanath and D-H. Lee for helpful discussions. This work was supported in part by the US Army Research Office through the Institute for Soldier Nanotechnologies (contract no.W911NF-07-D-0004). L.L. was supported in part by the Materials Research Science and Engineering Center of the National Science Foundation (award no. DMR-0819762). M.S. and L.L. were supported in part by the Massachusetts Institute of Technology S3TEC Energy Frontier Research Center of the US Department of Energy (grant no. DE-SC0001299). L.F. was supported by start-up funds from MIT.
Author information
Authors and Affiliations
Contributions
L.L. proposed the gyroid photonic crystal system for realizing Weyl points and performed the simulations. L.F. developed a low-energy k.p model for the proposed system. All authors contributed to the design of the study, discussion of the results and writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 638 kb)
Rights and permissions
About this article
Cite this article
Lu, L., Fu, L., Joannopoulos, J. et al. Weyl points and line nodes in gyroid photonic crystals. Nature Photon 7, 294–299 (2013). https://doi.org/10.1038/nphoton.2013.42
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2013.42
This article is cited by
-
Reconfigurable quantum fluid molecules of bound states in the continuum
Nature Physics (2024)
-
Analysis of Hermitian and non-Hermitian diabolic points and exceptional rings in parity-time symmetric ZRC and RLC dimers
Optical and Quantum Electronics (2024)
-
Topological classification for intersection singularities of exceptional surfaces in pseudo-Hermitian systems
Communications Physics (2023)
-
Real higher-order Weyl photonic crystal
Nature Communications (2023)
-
A second wave of topological phenomena in photonics and acoustics
Nature (2023)