Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Full characterization of polarization states of light via direct measurement

Nature Photonics volume 7, pages 316–321 (2013)Cite this article

Subjects

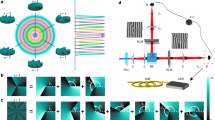
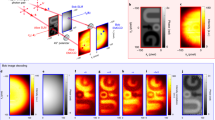
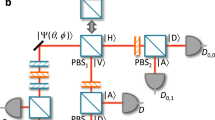
Abstract

Ascertaining the physical state of a system is vital in order to understand and predict its behaviour. However, due to their fragile nature, the direct observation of quantum states has, until recently, been elusive. Historically, determination of the quantum state has been performed indirectly through the use of tomography. We report on two experiments showing that an alternative approach can be used to determine the polarization quantum state in a simple, fast and general manner. The first experiment entails the direct measurement of the probability amplitudes describing pure polarization states of light, the first such measurement on a two-level system. The second experiment entails the direct measurement of the Dirac distribution (a phase-space quasi-probability distribution informationally equivalent to the density matrix), demonstrating that the direct measurement procedure is applicable to general (that is, potentially mixed) quantum states. Our work has applications to measurements in foundational quantum mechanics, quantum information and quantum metrology.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Prices vary by article type

from$1.95

to$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Schematic representation of the experiment.
Figure 2: Results of experiment 1 with linearly polarized probe states.
Figure 3: Measured states on the Poincaré sphere.
Figure 4: Results of experiment 2.

References

  1. D'Ariano, G. M., Paris, M. G. A. & Sacchi, M. F. Quantum tomography. Adv. Imag. Electron. Phys. 128, 205–308 (2003).

    Article  Google Scholar 

  2. Banaszek, K., D'Ariano, G. M., Paris, M. G. A. & Sacchi, M. F. Maximum-likelihood estimation of the density matrix. Phys. Rev. A 61, 010304 (1999).

    Article  Google Scholar 

  3. White, A. G., James, D. F. V., Munro, W. J. & Kwiat, P. G. Exploring Hilbert space: accurate characterization of quantum information. Phys. Rev. A 65, 012301 (2001).

    Article  ADS  MathSciNet  Google Scholar 

  4. Itatani, J. et al. Tomographic imaging of molecular orbitals. Nature 432, 867–871 (2004).

    Article  ADS  Google Scholar 

  5. Resch, K. J., Walther, P. & Zeilinger, A. Full characterization of a three-photon Greenberger–Horne–Zeilinger state using quantum state tomography. Phys. Rev. Lett. 94, 070402 (2005).

    Article  ADS  Google Scholar 

  6. Agnew, M., Leach, J., McLaren, M., Roux, F. S. & Boyd, R. W. Tomography of the quantum state of photons entangled in high dimensions. Phys. Rev. A 84, 062101 (2011).

    Article  ADS  Google Scholar 

  7. Lundeen, J. S., Sutherland, B., Patel, A., Stewart, C. & Bamber, C. Direct measurement of the quantum wavefunction. Nature 474, 188–191 (2011).

    Article  Google Scholar 

  8. Lundeen, J. S. & Bamber, C. Procedure for direct measurement of general quantum states using weak measurement. Phys. Rev. Lett. 108, 070402 (2012).

    Article  ADS  Google Scholar 

  9. Dirac, P. A. M. On the analogy between classical and quantum mechanics. Rev. Mod. Phys. 17, 195–199 (1945).

    Article  ADS  MathSciNet  Google Scholar 

  10. Chaturvedi, S. et al. Wigner–Weyl correspondence in quantum mechanics for continuous and discrete systems—a Dirac-inspired view. J. Phys. A 39, 1405–1423 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  11. Hofmann, H. F. Complex joint probabilities as expressions of reversible transformations in quantum mechanics. New J. Phys. 14, 043031 (2012).

    Article  ADS  Google Scholar 

  12. Feynman, R. P. Negative probability. In Quantum Implications: Essays in Honour of David Bohm Ch. 13 (eds Healy, B. J. & Peat, F. D.) 235–248 (Routledge, 1987).

    Google Scholar 

  13. Leonhardt, U. Quantum-state tomography and discrete Wigner function. Phys. Rev. Lett. 74, 4101–4105 (1995).

    Article  ADS  MathSciNet  Google Scholar 

  14. Mukamel, E., Banaszek, K., Walmsley, I. & Dorrer, C. Direct measurement of the spatial Wigner function with area-integrated detection. Opt. Lett. 28, 1317–1319 (2003).

    Article  ADS  Google Scholar 

  15. Smith, B. J., Killett, B., Raymer, M., Walmsley, I. & Banaszek, K. Measurement of the transverse spatial quantum state of light at the single-photon level. Opt. Lett. 30, 3365–3367 (2005).

    Article  ADS  Google Scholar 

  16. Aharonov, Y., Albert, D. Z. & Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351–1354 (1988).

    Article  ADS  Google Scholar 

  17. Duck, I. M., Stevenson, I. M. & Sudarshan, E. C. G. The sense in which a weak measurement of a spin-1/2 particle's spin component yields a value 100. Phys. Rev. D 40, 2112–2117 (1989).

    Article  ADS  Google Scholar 

  18. Knight, J. M. & Vaidman L. Weak easurement of photon polarization. Phys. Lett. A 143, 357–361 (1990).

    Article  ADS  Google Scholar 

  19. Ritchie, N. W. M., Story, J. G. & Hulet, R. G. Realization of a measurement of a weak value. Phys. Rev. Lett. 66, 1107–1110 (1991).

    Article  ADS  Google Scholar 

  20. Wiseman, H. Weak values, quantum trajectories, and the cavity-QED experiment on wave–particle correlation. Phys. Rev. A 65, 032111 (2002).

    Article  ADS  MathSciNet  Google Scholar 

  21. Solli, D. R., McCormick, C. F., Chiao, R. Y., Popescu, S. & Hickmann, J. M. Fast light, slow light, and phase singularities: A connection to generalized weak values. Phys. Rev. Lett. 92, 043601 (2004).

    Article  ADS  Google Scholar 

  22. Resch, K. J., Lundeen, J. S. & Steinberg, A. M. Experimental realization of the quantum box problem. Phys. Lett. A 324, 125–131 (2004).

    Article  ADS  Google Scholar 

  23. Johansen, L. Weak measurements with arbitrary probe states. Phys. Rev. Lett. 93, 120402 (2004).

    Article  ADS  Google Scholar 

  24. Pryde, G. J., O'Brien, J. L., White, A. G., Ralph, T. C. & Wiseman, H. M. Measurement of quantum weak values of photon polarization. Phys. Rev. Lett. 94, 220405 (2005).

    Article  ADS  Google Scholar 

  25. Hosten, O. & Kwiat, P. Observation of the spin hall effect of light via weak measurements. Science 319, 787–790 (2008).

    Article  ADS  Google Scholar 

  26. Dixon, P. B., Starling, D. J., Jordan, A. N. & Howell, J. C. Ultrasensitive beam deflection measurement via interferometric weak value amplification. Phys. Rev. Lett. 102, 173601 (2009).

    Article  ADS  Google Scholar 

  27. Popescu, S. Viewpoint: weak measurements just got stronger. Physics 2, 32 (2009).

    Article  Google Scholar 

  28. Kocsis, S. et al. Observing the average trajectories of single photons in a two-slit interferometer. Science 332, 1170–1173 (2011).

    Article  ADS  Google Scholar 

  29. Feizpour, A., Xing, X. & Steinberg, A. M. Amplifying single-photon nonlinearity using weak measurements. Phys. Rev. Lett. 107, 133603 (2011).

    Article  ADS  Google Scholar 

  30. De Gosson, M. A. & de Gosson, S. M. Weak values of a quantum observable and the cross-Wigner distribution. Phys. Lett. A 376, 293–296 (2012).

    Article  ADS  MathSciNet  Google Scholar 

  31. Edgar, M. P. et al. Imaging high-dimensional spatial entanglement with a camera. Nature Commun. 3, 984 (2012).

    Article  ADS  Google Scholar 

  32. Lundeen J. S. & Resch, K. J. Practical measurement of joint weak values and their connection to the annihilation operator. Phys. Lett. A 334, 337–344 (2005).

    Article  ADS  Google Scholar 

  33. Wootters, W. K. & Fields, B. D. Optimal state-determination by mutually unbiased measurements. Ann. Phys. 191, 363–381 (1989).

    Article  ADS  MathSciNet  Google Scholar 

  34. Geszti, T. Postselected weak measurement beyond the weak value. Phys. Rev. A 81, 044102 (2010).

    Article  ADS  Google Scholar 

  35. Agnew, M., Leach, J. & Boyd, R. W. Observation of entanglement witnesses for orbital angular momentum states. Eur. Phys. J. D 66, 156 (2012).

    Article  ADS  Google Scholar 

  36. Simmons, S. et al. Entanglement in a solid-state spin ensemble. Nature 470, 69–72 (2011).

    Article  ADS  Google Scholar 

  37. Steger, M. Quantum information storage for over 180 s using donor spins in a 28Si ‘semiconductor vacuum’. Science 336, 1280–1283 (2012).

    Article  ADS  Google Scholar 

  38. Di Lorenzo, A. Full counting statistics of weak-value measurement. Phys. Rev. A 85, 032106 (2012).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors thank K. Piché and F. Miatto for helpful discussions, and P.B. Corkum and C. Zhang for lending us the quartz crystal. This work was supported by the Canada Excellence Research Chairs (CERC) Program. In addition, R.W.B. acknowledges support from the DARPA InPho program.

Author information

Authors and Affiliations

  1. Department of Physics, University of Ottawa, Ottawa, K1N 6N5, Canada

    Jeff Z. Salvail, Megan Agnew, Allan S. Johnson, Eliot Bolduc, Jonathan Leach & Robert W. Boyd

  2. Institute of Optics, University of Rochester, Rochester, 14627, New York, USA

    Robert W. Boyd

Authors
  1. Jeff Z. Salvail
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Megan Agnew
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Allan S. Johnson
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Eliot Bolduc
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jonathan Leach
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Robert W. Boyd
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.Z.S. initiated the study. The experiment was designed by J.Z.S., A.S.J., E.B. and J.L. The experiment was performed by J.Z.S., M.A. and A.S.J., and data analysis was performed by J.Z.S. R.W.B. supervised all aspects of the project. All authors contributed to the text of the manuscript.

Corresponding author

Correspondence to Jeff Z. Salvail.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 736 kb)

Rights and permissions

Reprints and Permissions

About this article

Cite this article

Salvail, J., Agnew, M., Johnson, A. et al. Full characterization of polarization states of light via direct measurement. Nature Photon 7, 316–321 (2013). https://doi.org/10.1038/nphoton.2013.24

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphoton.2013.24

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing