Abstract
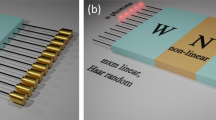
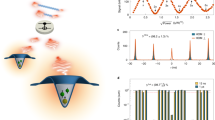
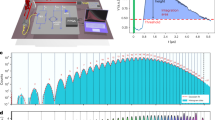
Universal quantum computers1 promise a dramatic increase in speed over classical computers, but their full-size realization remains challenging2. However, intermediate quantum computational models3,4,5 have been proposed that are not universal but can solve problems that are believed to be classically hard. Aaronson and Arkhipov6 have shown that interference of single photons in random optical networks can solve the hard problem of sampling the bosonic output distribution. Remarkably, this computation does not require measurement-based interactions7,8 or adaptive feed-forward techniques9. Here, we demonstrate this model of computation using laser-written integrated quantum networks that were designed to implement unitary matrix transformations. We characterize the integrated devices using an in situ reconstruction method and observe three-photon interference10,11,12 that leads to the boson-sampling output distribution. Our results set a benchmark for a type of quantum computer with the potential to outperform a conventional computer through the use of only a few photons and linear-optical elements13.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Knill, E. & Laflamme, R. Power of one bit of quantum information. Phys. Rev. Lett. 81, 5672–5675 (1998).
Aaronson, S. & Gottesman, D. Improved simulation of stabilizer circuits. Phys. Rev. A 70, 052328 (2004).
Jordan, S. P. Permutational quantum computing. Quant. Infor. Comput. 10, 470–497 (2010).
Aaronson, S. & Arkhipov, A. in Proceedings of the 43rd Annual ACM Symposium on Theory of Computing 333–342 (ACM, 2011).
Gasparoni, S., Pan, J-W., Walther, P., Rudolph, T. & Zeilinger, A. Realization of a photonic controlled-NOT gate sufficient for quantum computation. Phys. Rev. Lett. 93, 020504 (2004).
Okamoto, R., O'Brien, J., Hofmann, H. & Takeuchi, S. Realization of a Knill–Laflamme–Milburn controlled-NOT photonic quantum circuit combining effective optical nonlinearities. Proc. Natl Acad. Sci. USA 108, 10067–10071 (2011).
Prevedel, R. et al. High-speed linear optics quantum computing using active feed-forward. Nature 445, 65–69 (2007).
Metcalf, B. J. et al. Multiphoton quantum interference in a multiport integrated photonic device. Nat. Commun. 4, 1356 (2013).
Spagnolo, N. et al. Three-photon bosonic coalescence in an integrated tritter. Preprint at http://lanl.arxiv.org/abs/1210.6935 (2012).
Spagnolo, N. et al. Quantum interferometry with three-dimensional geometry. Sci. Rep. 2, 862 (2012).
Rohde, P. P. & Ralph, T. C. Error tolerance of the boson-sampling model for linear optics quantum computing. Phys. Rev. A 85, 022332 (2012).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Gao, W. et al. Teleportation-based realization of an optical quantum two-qubit entangling gate. Proc. Natl Acad. Sci. USA 107, 20869–20874 (2010).
Yoran, N. & Reznik, B. Deterministic linear optics quantum computation with single photon qubits. Phys. Rev. Lett. 91, 037903 (2003).
Nielsen, M. A. Optical quantum computation using cluster states. Phys. Rev. Lett. 93, 040503 (2004).
Browne, D. E. & Rudolph, T. Resource-efficient linear optical quantum computation. Phys. Rev. Lett. 95, 010501 (2005).
Ralph, T. C., Hayes, A. J. F. & Gilchrist, A. Loss-tolerant optical qubits. Phys. Rev. Lett. 95, 100501 (2005).
O'Brien, J. L., Furusawa, A. & Vuckovic, J. Photonic quantum technologies. Nature Photon. 3, 687–695 (2009).
Aaronson, S. A linear-optical proof that the permanent is #P-hard. Proc. R. Soc. A 467, 3393–3405 (2011).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Zeilinger, A. General properties of lossless beam splitters in interferometry. Am. J. Phys. 49, 882–883 (1981).
Arkhipov, A. & Kuperberg, G. The bosonic birthday paradox. Geom. Topol. Monog. 18, 1–7 (2012).
Itoh, K., Watanabe, W., Nolte, S. & Schaffer, C. Ultrafast processes for bulk modification of transparent materials. MRS Bull. 31, 620–625 (2006).
Marshall, G. et al. Laser written waveguide photonic quantum circuits. Opt. Express 17, 12546–12554 (2009).
Reck, M. et al. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58–61 (1994).
Kwiat, P. G. et al. New high-intensity source of polarization-entangled photon pairs. Phys. Rev. Lett. 75, 4337–4341 (1995).
Laing, A. & O'Brien, J. L. Super-stable tomography of any linear optical device. Preprint at http://lanl.arxiv.org/abs/1208.2868 (2012).
Spring, J. B. et al. Boson sampling on a photonic chip. Science 339, 798–801 (2013).
Broome, M. A. et al. Photonic boson sampling in a tunable circuit. Science 339, 794–798 (2013).
Crespi, A. et al. Experimental boson sampling in arbitrary integrated photonic circuits. Nature Photon. http://dx.doi.org/10.1038/nphoton.2013.112 (in the press); preprint at http://lanl.arxiv.org/abs/1212.2783 (2012).
Acknowledgements
The authors thank S. Aaronson, Č. Brukner and M. Ringbauer for discussions. The authors acknowledge support from the European Commission under projects ‘Q-ESSENCE—Quantum Interfaces, Sensors, and Communication based on Entanglement’ (no. 248095), ‘QuILMI—Quantum Integrated Light Matter Interface’ (no. 295293) and the ERA-Net CHIST-ERA project ‘QUASAR—Quantum States: Analysis and Realizations’, the German Ministry of Education and Research (Center for Innovation Competence program, grant no. 03Z1HN31), the John Templeton Foundation, the Vienna Center for Quantum Science and Technology (VCQ), the Austrian Nano-initiative ‘Nanostructures of Atomic Physics (NAP-PLATON)’ and the Austrian Science Fund (FWF) under projects ‘SFB-FoQuS—Foundations and Applications of Quantum Science’, ‘PhoQuSi—Photonic Quantum Simulators (Y585-N20)’ and the doctoral programme ‘CoQuS—Complex Quantum Systems’, the Vienna Science and Technology Fund (WWTF; under grant no. ICT12-041), and the Air Force Office of Scientific Research, Air Force Material Command, United States Air Force (grant no. FA8655-11-1-3004).
Author information
Authors and Affiliations
Contributions
M.T. designed and carried out the experiment, analysed data and waveguide structures, and wrote the manuscript. B.D. provided the theoretical analysis, analysed data and waveguide structures, and wrote the manuscript. R.H. designed and prepared the waveguide structures. S.N. and A.S. supervised the design and preparation of the waveguide structures. P.W. supervised the project, designed the experiment and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 2505 kb)
Rights and permissions
About this article
Cite this article
Tillmann, M., Dakić, B., Heilmann, R. et al. Experimental boson sampling. Nature Photon 7, 540–544 (2013). https://doi.org/10.1038/nphoton.2013.102
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2013.102
This article is cited by
-
Efficiently simulating the work distribution of multiple identical bosons with boson sampling
Frontiers of Physics (2024)
-
Non-linear Boson Sampling
npj Quantum Information (2023)
-
Practical advantage of quantum machine learning in ghost imaging
Communications Physics (2023)
-
Quantum simulation of thermodynamics in an integrated quantum photonic processor
Nature Communications (2023)
-
Single-photon detection using high-temperature superconductors
Nature Nanotechnology (2023)