Abstract
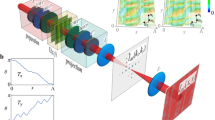
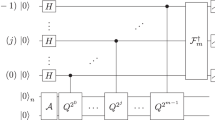
A quantum algorithm solves computational tasks using fewer physical resources than the best-known classical algorithm. Of most interest are those for which an exponential reduction is achieved. The key example is the phase estimation algorithm, which provides the quantum speedup in Shor's factoring algorithm and quantum simulation algorithms. To date, fully quantum experiments of this type have demonstrated only the read-out stage of quantum algorithms, but not the steps in which input data is read in and processed to calculate the final quantum state. Indeed, knowing the answer beforehand was essential. We present a photonic demonstration of a full quantum algorithm—the iterative phase estimation algorithm (IPEA)—without knowing the answer in advance. This result suggests practical applications of the phase estimation algorithm, including quantum simulations and quantum metrology in the near term, and factoring in the long term.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Vandersypen, L. M. K. et al. Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887 (2001).
Lu, C.-Y., Browne, D. E., Yang, T., & Pan, J.-W. Demonstration of a compiled version of Shor's quantum factoring algorithm using photonic qubits. Phys. Rev. Lett. 99, 250504 (2007).
Lanyon, B. P. et al. Experimental demonstration of a compiled version of Shor's algorithm with quantum entanglement. Phys. Rev. Lett. 99, 250505 (2007).
Politi, A., Matthews, J. C. F. & O'Brien, J. L. Shor's quantum factoring algorithm on a photonic chip. Science 325, 1221 (2009).
Lanyon, B. P. et al. Towards quantum chemistry on a quantum computer. Nature Chem. 2, 106–111 (2010).
Du, J. et al. NMR implementation of a molecular hydrogen quantum simulation with adiabatic state preparation. Phys. Rev. Lett. 104, 030502 (2010).
Li, Z. et al. Solving quantum ground-state problems with nuclear magnetic resonance. Sci. Rep. 1, 88 (2011).
Griffiths, R. B. & Niu, C.-S. Semiclassical Fourier transform for quantum computation. Phys. Rev. Lett. 76, 3228–3231 (1996).
Dobŝíĉek, M., Johansson, G., Shumeiko, V., & Wendin, G. Arbitrary accuracy iterative quantum phase estimation algorithm using a single ancillary qubit: a two-qubit benchmark. Phys. Rev. A 76, 030306 (2007).
Ralph, T. C., Resch, K. J. & Gilchrist, A. Efficient Toffoli gates using qudits. Phys. Rev. A 75, 022313 (2007).
Lanyon, B. P. et al. Simplifying quantum logic using higher-dimensional Hilbert spaces. Nature Phys. 5, 134–140 (2009).
Zhou, X.-Q. et al. Adding control to arbitrary unknown quantum operations. Nature Commun. 2, 413 (2011).
Higgins, B. L., Berry, D. W., Bartlett, S. D., Wiseman, H. M. & Pryde, G. J. Entanglement-free Heisenberg-limited phase estimation. Nature 450, 393–396 (2007).
Gao, W. et al. Experimental demonstration of a hyper-entangled ten-qubit Schrödinger cat state. Nature Phys. 6, 331–335 (2010).
Abrams, D. S. & Lloyd, S. Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors. Phys. Rev. Lett. 83, 5162–5165 (1999).
Politi, A., Cryan, M. J., Rarity, J. G., Yu, S., & O'Brien, J. L. Silica-on-silicon waveguide quantum circuits. Science 320, 646–649 (2008).
Matthews, J. C. F., Politi, A., Stefanov, A., & O'Brien, J. L. Manipulation of multiphoton entanglement in waveguide quantum circuits. Nature Photon. 3, 346–350 (2009).
Shadbolt, P. et al. Generating, manipulating and measuring entanglement and mixture with a reconfigurable photonic circuit. Nature Photon. 6, 45–49 (2011).
Lobino, M. et al. Correlated photon-pair generation in a periodically poled MgO doped stoichiometric lithium tantalate reverse proton exchanged waveguide. Appl. Phys. Lett. 99, 081110 (2011).
Engin, E. et al. Photon pair generation in silicon microring resonator and enhancement via reverse bias. Preprint at http://arXiv.org/abs/1204.4922 (2012).
Parker, S., & Plenio, M. B. Efficient factorization with a single pure qubit and logN mixed qubits. Phys. Rev. Lett. 85, 3049–3052 (2000).
Shields, A. J. Semiconductor quantum light sources. Nature Photon. 1, 215–223 (2007).
Hadfield, R. Single-photon detectors for optical quantum information applications. Nature Photon. 3, 696–705 (2009).
Knill, E., Laflamme, R., & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Acknowledgements
The authors thank P.J. Shadbolt for writing the quantum process tomography code and J.C.F. Matthews, A. Peruzzo, G.J. Pryde and P. Zhang for helpful discussions. This work was supported by the Engineering and Physical Sciences Research Council (EPSRC), the European Research Council (ERC), PHORBITECH, Quantum Interfaces, Sensors, and Communication based on Entanglement (QESSENCE) and the Centre for Nanoscience and Quantum Information (NSQI). J.O'B. acknowledges a Royal Society Wolfson Merit Award.
Author information
Authors and Affiliations
Contributions
The theory was developed by X.-Q.Z. and T.C.R. The theory was mapped to the experimental circuit by X.-Q.Z., P.K., T.C.R. and J.O.B. Experiments were performed by X.-Q.Z. and P.K. Data were analysed by X.-Q.Z., P.K., T.C.R. and J.O.B. The manuscript was written by X.-Q.Z., P.K., T.C.R. and J.O.B. The project was supervised by X.-Q.Z. and J.O.B.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 424 kb)
Rights and permissions
About this article
Cite this article
Zhou, XQ., Kalasuwan, P., Ralph, T. et al. Calculating unknown eigenvalues with a quantum algorithm. Nature Photon 7, 223–228 (2013). https://doi.org/10.1038/nphoton.2012.360
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2012.360
This article is cited by
-
A programmable qudit-based quantum processor
Nature Communications (2022)
-
Multi-qubit entanglement and algorithms on a neutral-atom quantum computer
Nature (2022)
-
Recent advances for quantum classifiers
Science China Physics, Mechanics & Astronomy (2022)
-
A hybrid algorithm to solve linear systems of equations with limited qubit resources
Quantum Information Processing (2022)
-
Alternative scheme of universal optical programmable multi-qubit gates for polarization qubits
Quantum Information Processing (2020)