Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Limits on classical communication from quantum entropy power inequalities

Nature Photonics volume 7, pages 142–146 (2013)Cite this article

Subjects

An Erratum to this article was published on 27 February 2013

This article has been updated

Abstract

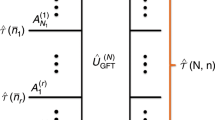
Almost all modern communication systems rely on electromagnetic fields. The additive white Gaussian noise (AWGN) channel is often a good approximate description of such a system, and its information-carrying capacity is given by a simple formula. The quantum analogue of AWGN channels, the bosonic Gaussian noise channel, accurately describes many quantum optical communication systems of interest. Estimating its capacity is significantly more difficult; although some simple coding strategies are known, whether or not more sophisticated techniques could dramatically improve communication rates has been unknown. Here, we present strong new upper bounds for the classical capacity of bosonic Gaussian noise channels. These results imply that known coding techniques are typically close to optimal. Our main technical tool is an entropy power inequality bounding the entropy produced as two quantum signals combine at a beamsplitter. Its proof relies on a quantum diffusion process which smooths arbitrary states towards Gaussians.

This is a preview of subscription content, access via your institution

Access options

Rent or buy this article

Prices vary by article type

from$1.95

to$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Two independent quantum signals combined at a beamsplitter.
Figure 2: An additive noise channel arises when an input signal A interacts via a beamsplitter with initial environment Ein followed by a partial trace over Eout resulting in an output signal B.
Figure 3: Known bounds on the classical capacity of thermal noise channels.
Figure 4: Using the evolution of the inputs and output of a beamsplitter under diffusion to prove the quantum entropy power inequality.

Similar content being viewed by others

Change history

  • 24 January 2013

    In the version of this Article originally published, the author affiliations were incorrect and should have read: 1IBM TJ Watson Research Center, 1101 Kitchawan Road, Yorktown Heights, New York 10598, USA, 2Institute for Quantum Computing and Department of Applied Mathematics, University of Waterloo, ON, Canada, N2L3G1. This has now been corrected in the HTML and PDF versions of the Article.

References

  1. Shannon, C. E. A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423, 623–656 (1948).

    Article  MathSciNet  Google Scholar 

  2. Pierce, J. The early days of information theory. IEEE Trans. Inf. Theory 19, 3–8 (1973).

    Article  MathSciNet  Google Scholar 

  3. Schumacher, B. & Westmoreland, M. D. Sending classical information via noisy quantum channels. Phys. Rev. A 56, 131–138 (1997).

    Article  ADS  Google Scholar 

  4. Holevo, A. The capacity of the quantum channel with general signal states. IEEE Trans. Inf. Theory 44, 269–273 (1998).

    Article  MathSciNet  Google Scholar 

  5. Hastings, M. B. Superadditivity of communication capacity using entangled inputs. Nature Phys. 5, 255–257 (2009).

    Article  ADS  Google Scholar 

  6. Holevo, A. S. & Werner, R. F. Evaluating capacities of bosonic Gaussian channels. Phys. Rev. A 63, 032312 (2001).

    Article  ADS  Google Scholar 

  7. Eisert, J. & Wolf, M. M. Gaussian quantum channels. Preprint at http://arxiv.org/abs/quant-ph/0505151 (2005).

  8. Giovannetti, V. et al. Classical capacity of the lossy bosonic channel: the exact solution. Phys. Rev. Lett. 92, 027902 (2004).

    Article  ADS  Google Scholar 

  9. Stam, A. Some inequalities satisfied by the quantities of information of Fisher and Shannon. Inform. Control 2, 101–112 (1959).

    Article  MathSciNet  Google Scholar 

  10. Blachman, N. The convolution inequality for entropy powers. IEEE Trans. Inf. Theory 11, 267–271 (1965).

    Article  MathSciNet  Google Scholar 

  11. Verdu, S. & Guo, D. A simple proof of the entropy-power inequality. IEEE Trans. Inf. Theory 52, 2165–2166 (2006).

    Article  MathSciNet  Google Scholar 

  12. Rioul, O. Information theoretic proofs of entropy power inequalities. IEEE Trans. Inf. Theory 57, 33–55 (2011).

    Article  MathSciNet  Google Scholar 

  13. Bergmans, P. A simple converse for broadcast channels with additive white Gaussian noise (corresp.). IEEE Trans. Inf. Theory 20, 279–280 (1974).

    Article  MathSciNet  Google Scholar 

  14. Leung-Yan-Cheong, S. & Hellman, M. The Gaussian wire-tap channel. IEEE Trans. Inf. Theory 24, 451–456 (1978).

    Article  MathSciNet  Google Scholar 

  15. Dembo, A., Cover, T. & Thomas, J. Information theoretic inequalities. IEEE Trans. Inf. Theory 37, 1501–1518 (1991).

    Article  MathSciNet  Google Scholar 

  16. Wolf, M. M., Giedke, G. & Cirac, J. I. Extremality of Gaussian quantum states. Phys. Rev. Lett. 96, 080502 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  17. Giovannetti, V., Holevo, A., Lloyd, S. & Maccone, L. Generalized minimal output entropy conjecture for one-mode Gaussian channels: definitions and some exact results. J. Phys. A 43, 032315 (2010).

    Article  MathSciNet  Google Scholar 

  18. Barron, A. R. Monotonic Central Limit Theorem for Densities, Department of Statistics Technical Report 50 (Stanford University, 1984).

    Google Scholar 

  19. Wehrl, A. General properties of entropy. Rev. Mod. Phys. 50, 221–260 (1978).

    Article  ADS  MathSciNet  Google Scholar 

  20. Smith, G. & Smolin, J. in Information Theory Workshop 368–372 (Porto, 2008).

    Google Scholar 

  21. King, C. & Ruskai, M. Minimal entropy of states emerging from noisy quantum channels. IEEE Trans. Inf. Theory 47, 192–209 (2001).

    Article  MathSciNet  Google Scholar 

  22. Shor, P. Equivalence of additivity questions in quantum information theory. Commun. Math. Phys. 246, 453–472 (2004).

    Article  ADS  MathSciNet  Google Scholar 

  23. Giovannetti, V., Guha, S., Lloyd, S., Maccone, L. & Shapiro, J. H. Minimum output entropy of bosonic channels: a conjecture. Phys. Rev. A 70, 415305 (2004).

    Google Scholar 

  24. Petz, D. Covariance and Fisher information in quantum mechanics. J. Phys. A 35, 929–939 (2002).

    Article  ADS  MathSciNet  Google Scholar 

  25. König, R. & Smith, G. The entropy power inequality for quantum systems. Preprint at http://www.arxiv.org/abs/1205.3409 (2012).

  26. Hall, M. J. W. Quantum properties of classical Fisher information. Phys. Rev. A 62, 012107 (2000).

    Article  ADS  MathSciNet  Google Scholar 

  27. Zamir, R. A proof of the fisher information inequality via a data processing argument. IEEE Trans. Inf. Theory 44, 1246–1250 (1998).

    Article  MathSciNet  Google Scholar 

  28. Guha, S., Shapiro, J. & Erkmen, B. in Proceedings of Information Theory 2008, IEEE International Symposium on Information Theory, 91–95 (2008).

  29. Serafini, A., Eisert, J. & Wolf, M. M. Multiplicativity of maximal output purities of Gaussian channels under Gaussian inputs. Phys. Rev. A 71, 012320 (2005).

    Article  ADS  Google Scholar 

  30. Smith, G., Smolin, J. A. & Yard, J. Quantum communication with Gaussian channels of zero quantum capacity. Nature Photon. 5, 624–627 (2011).

    Article  ADS  Google Scholar 

  31. Costa, M. A new entropy power inequality. IEEE Trans. Inf. Theory 31, 751–760 (1985).

    Article  MathSciNet  Google Scholar 

  32. Yard, J., Hayden, P. & Devetak, I. Quantum broadcast channels. IEEE Trans. Inf. Theory 57, 7147–7162 (2011).

    Article  MathSciNet  Google Scholar 

  33. Hudson, R. L. A quantum-mechanical central limit theorem for anti-commuting observables. J. Appl. Probab. 10, 502–509 (1973).

    Article  MathSciNet  Google Scholar 

  34. Barron, A. Entropy and the Central Limit Theorem. Ann. Probab. 14, 336–342 (1986).

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors thank C. Bennett, J. Gambetta and J. Smolin for helpful comments and S. Guha for discussions. Both authors were supported by the Defense Advance Research Projects Agency Quantum Entanglement Science and Technology programme (contract no. HR0011-09-C-0047).

Author information

Authors and Affiliations

  1. IBM TJ Watson Research Center, 1101 Kitchawan Road, Yorktown Heights, 10598, New York, USA

    Robert König & Graeme Smith

  2. Institute for Quantum Computing and Department of Applied Mathematics, University of Waterloo, N2L3G1, ON, Canada

    Robert König

Authors
  1. Robert König
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Graeme Smith
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

R.K. and G.S. designed and carried out the research and wrote the paper.

Corresponding authors

Correspondence to Robert König or Graeme Smith.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 539 kb)

Rights and permissions

Reprints and Permissions

About this article

Cite this article

König, R., Smith, G. Limits on classical communication from quantum entropy power inequalities. Nature Photon 7, 142–146 (2013). https://doi.org/10.1038/nphoton.2012.342

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphoton.2012.342

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing