Abstract
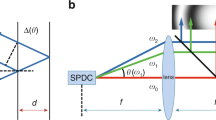
The Law of Reflection of a light ray incident upon a mirror (θin = θout) was first formulated by Euclid around 300 bc in his book Catoptrics1; it has been a tenet of geometrical optics ever since. However, more recently, a small angular deviation of the Law of Reflection has been predicted for a physical light beam when this is regarded as the implementation of a ray2,3,4,5. The deviation is a diffractive consequence of the angular dependence of the reflectivity and should occur for any mirror with less than 100% reflectivity. We report here experimental proof of this angular deviation by determining the direction of an optical beam after reflection from an air–glass interface, using a position detector with nanometre resolution. Our results are relevant for angular metrology in general and cantilever-based surface microscopies in particular. Analogous angular deviations are expected for reflection of acoustic waves and quantum matter waves.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Hecht, E. Optics 4th edn, 1 (Addison-Wesley, 2002).
Ra, J. W., Bertoni, H. L. & Felsen, L. B. Reflection and transmission of beams at a dielectric interface. SIAM J. Appl. Math. 24, 396–413 (1973).
Antar, Y. M. & Boerner, W. M. Gaussian beam interaction with a planar dielectric interface. Can. J. Phys. 52, 962–972 (1974).
Chan, C. C. & Tamir, C. Angular shift of a Gaussian beam reflected near the Brewster angle. Opt. Lett. 10, 378–380 (1985).
Aiello, A. & Woerdman, J. P. Role of beam propagation in Goos–Hänchen and Imbert–Fedorov shifts. Opt. Lett. 33, 1437–1439 (2008).
Goos, F. & Hänchen, H. Ein neuer und fundamentaler Versuch zur Totalreflexion. Ann. Phys. (Leipzig) 1, 333–346 (1947).
Artmann, K. Berechnung der Seitenversetzung des totalreflektierten Strahles. Ann. Phys. 2, 87–102 (1948).
Bonnet, C., Chauvat, D., Emile, O., Bretenaker, F. & Le Floch, A. Measurement of positive and negative Goos–Hänchen effects for metallic gratings near Wood anomalies. Opt. Lett. 26, 666–668 (2001).
Berman, P. R. Goos–Hänchen shifts in negatively refracting media. Phys. Rev. E 66, 067603 (2002).
Bliokh, K. Y., Shadrivov, I. V. & Kivshar, Y. S. Goos–Hänchen and Imbert–Fedorov shifts of polarized vortex beams. Opt. Lett. 34, 389–391 (2009).
Jost, B. M., Al-Rashed, A. A. R. & Saleh, B. E. A. Observation of the Goos–Hänchen effect in a phase-conjugate mirror. Phys. Rev. Lett. 81, 2233–2235 (1998).
Huang, J., Duan, Z., Ling, H. & Zhang, W. Goos–Hänchen-like shifts in atom optics. Phys. Rev. A 77, 063608 (2008).
Felbacq, D., Moreau, A. & Smaâli, R. Goos–Hänchen effect in the gaps of photonic crystals. Opt. Lett. 28, 1633–1635 (2003).
Emile, O., Galstyan, T., Le Floch, A. & Bretenaker, F. Measurement of the nonlinear Goos–Hänchen effect for Gaussian optical beams. Phys. Rev. Lett. 75, 1511–1514 (1995).
Yin, X. & Hesselink, L. Large positive and negative lateral optical beam displacements due to surface plasmon resonance. Appl. Phys. Lett. 85, 372–374 (2004).
Gragg, R. F. The total reflection of a compact wave group: Long-range transmission in a waveguide. Am. J. Phys. 56, 1092–1094 (1988).
Merano, M. et al. Observation of Goos–Hänchen shifts in metallic reflection. Opt. Express 15, 15928–15934 (2007).
Aiello, A. & Woerdman, J. P. Theory of angular Goos–Hänchen shift near Brewster incidence. Preprint at <http://arxiv.org/pdf/0903.3730>.
Müller, D., Tharanga D., Stahlhofen, A. A. & Nimtz, G. Nonspecular shifts of microwaves in partial reflection. Europhys. Lett. 73, 526–532 (2006).
Mandel, L. & Wolf, E. Optical Coherence and Quantum Optics Vol. 143, 271 (Cambridge Univ. Press, 1995).
Fainman, Y. & Shamir, J. Polarization of nonplanar wavefronts. Appl. Opt. 23, 3188–3195 (1984).
Li, Q. & Vernon, R. J. Theoretical and experimental investigation of Gaussian beam transmission and reflection by a dielectric slab at 110 GHz. IEEE Trans. Antennas Propag. 54, 3449–3457 (2006).
Mueller, F., Heugel, S. & Wang, L. J. Femto-newton light force measurement at the thermal noise limit. Opt. Lett. 33, 539–541 (2008).
Putman, C. A. J., De Grooth, B. G., Van Hulst, N. F. & Greve, J. A theoretical comparison between interferometric and optical beam deflection technique for the measurement of cantilever displacement in AFM. Ultramicroscopy 42, 1509–1513 (1992).
Centrella, J. M. Resource letter: GrW-1: Gravitational waves. Am. J. Phys. 71, 520–524 (2003).
Acknowledgements
This work was supported by the Netherlands Foundation for Fundamental Research of Matter (FOM) and by the Seventh Framework Programme for Research of the European Commission, under the FET-Open grant agreement HIDEAS, no. FP7-ICT-221906. We acknowledge E.R. Eliel and G.'t Hooft for useful discussions.
Author information
Authors and Affiliations
Corresponding authors
Supplementary information
Rights and permissions
About this article
Cite this article
Merano, M., Aiello, A., van Exter, M. et al. Observing angular deviations in the specular reflection of a light beam. Nature Photon 3, 337–340 (2009). https://doi.org/10.1038/nphoton.2009.75
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2009.75
This article is cited by
-
Enhanced Goos-Hänchen Shift of SPR Sensor with TMDCs and Doped PANI/Chitosan Composites for Heavy Metal Ions Detection in Aquatic Environment
Plasmonics (2023)
-
Theoretical Study of Spatial and Angular Goos-Hänchen Shifts in Quantum System
International Journal of Theoretical Physics (2021)
-
Large tunable lateral shift in prism coupling system containing a superconducting slab
Applied Physics B (2020)
-
Electrically Control Lateral Shift Owning to Guided-Wave Surface Plasmon Resonance with a Lithium Niobate Prism
Plasmonics (2020)
-
Geometric phase from Aharonov–Bohm to Pancharatnam–Berry and beyond
Nature Reviews Physics (2019)