Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Automated determination of fibrillar structures by simultaneous model building and fiber diffraction refinement

Nature Methods volume 12, pages 679–684 (2015)Cite this article

Subjects

Abstract

For highly oriented fibrillar molecules, three-dimensional structures can often be determined from X-ray fiber diffraction data. However, because of limited information content, structure determination and validation can be challenging. We demonstrate that automated structure determination of protein fibers can be achieved by guiding the building of macromolecular models with fiber diffraction data. We illustrate the power of our approach by determining the structures of six bacteriophage viruses de novo using fiber diffraction data alone and together with solid-state NMR data. Furthermore, we demonstrate the feasibility of molecular replacement from monomeric and fibrillar templates by solving the structure of a plant virus using homology modeling and protein-protein docking. The generated models explain the experimental data to the same degree as deposited reference structures but with improved structural quality. We also developed a cross-validation method for model selection. The results highlight the power of fiber diffraction data as structural constraints.

This is a preview of subscription content, access via your institution

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Macromolecular modeling plays a large role in structure determination from fiber diffraction data.
Figure 2: Fiber diffraction intensity calculations in real and reciprocal space at a given layer line.
Figure 3: Cross-validation with χ2free.
Figure 4: De novo structure determination of bacteriophages.
Figure 5: Molecular replacement of hibiscus latent Singapore virus.

Accession codes

Accessions

Protein Data Bank

References

  1. Chandrasekaran, R. & Stubbs., G. in International Tables for Crystallography Vol. F, 2nd edn. (eds. Arnold, E., Himmel, D.M. & Rossmann, M.G.) Ch. 19.5, 583–592 (International Union of Crystallography, 2012).

  2. Brünger, A.T. Free R value: cross-validation in crystallography. Methods Enzymol. 277, 366–396 (1997).

    Article  Google Scholar 

  3. Wang, H. & Stubbs, G. Structure determination of cucumber green mottle mosaic virus by X-ray fiber diffraction. Significance for the evolution of tobamoviruses. J. Mol. Biol. 239, 371–384 (1994).

    Article  CAS  Google Scholar 

  4. Kaufmann, K.W., Lemmon, G.H., Deluca, S.L., Sheehan, J.H. & Meiler, J. Practically useful: what the Rosetta protein modeling suite can do for you. Biochemistry 49, 2987–2998 (2010).

    Article  CAS  Google Scholar 

  5. Bradley, P., Misura, K.M.S. & Baker, D. Toward high-resolution de novo structure prediction for small proteins. Science 309, 1868–1871 (2005).

    Article  CAS  Google Scholar 

  6. Kuhlman, B. et al. Design of a novel globular protein fold with atomic-level accuracy. Science 302, 1364–1368 (2003).

    Article  CAS  Google Scholar 

  7. Welsh, L.C., Symmons, M.F. & Marvin, D.A. The molecular structure and structural transition of the á-helical capsid in filamentous bacteriophage Pf1. Acta Crystallogr. D Biol. Crystallogr. 56, 137–150 (2000).

    Article  CAS  Google Scholar 

  8. Welsh, L.C., Symmons, M.F., Sturtevant, J.M., Marvin, D.A. & Perham, R.N. Structure of the capsid of Pf3 filamentous phage determined from X-ray fibre diffraction data at 3.1 Å resolution. J. Mol. Biol. 283, 155–177 (1998).

    Article  CAS  Google Scholar 

  9. Wu, Y. & Ma, J. Refinement of F-actin model against fiber diffraction data by long-range normal modes. Biophys. J. 86, 116–124 (2004).

    Article  CAS  Google Scholar 

  10. Makowski, L. The use of continuous diffraction data as a phase constraint. II. Application to fiber diffraction data. J. Appl. Crystallogr. 15, 546–557 (1982).

    Article  CAS  Google Scholar 

  11. Tyka, M.D. et al. Alternate states of proteins revealed by detailed energy landscape mapping. J. Mol. Biol. 405, 607–618 (2011).

    Article  CAS  Google Scholar 

  12. Chen, V.B. et al. MolProbity: all-atom structure validation for macromolecular crystallography. Acta Crystallogr. D Biol. Crystallogr. 66, 12–21 (2010).

    Article  CAS  Google Scholar 

  13. Falkner, B. & Schröder, G.F. Cross-validation in cryo-EM-based structural modeling. Proc. Natl. Acad. Sci. USA 110, 8930–8935 (2013).

    Article  CAS  Google Scholar 

  14. Fabiola, F., Korostelev, A. & Chapman, M.S. Bias in cross-validated free R factors: mitigation of the effects of non-crystallographic symmetry. Acta Crystallogr. D Biol. Crystallogr. 62, 227–238 (2006).

    Article  Google Scholar 

  15. Marvin, D.A., Welsh, L.C., Symmons, M.F., Scott, W.R.P. & Straus, S.K. Molecular structure of fd (f1, M13) filamentous bacteriophage refined with respect to X-ray fibre diffraction and solid-state NMR data supports specific models of phage assembly at the bacterial membrane. J. Mol. Biol. 355, 294–309 (2006).

    Article  CAS  Google Scholar 

  16. Straus, S.K., Scott, W.R.P., Schwieters, C.D. & Marvin, D.A. Consensus structure of Pf1 filamentous bacteriophage from X-ray fibre diffraction and solid-state NMR. Eur. Biophys. J. 40, 221–234 (2011).

    Article  CAS  Google Scholar 

  17. Straus, S.K., Scott, W.R.P., Symmons, M.F. & Marvin, D.A. On the structures of filamentous bacteriophage Ff (fd, f1, M13). Eur. Biophys. J. 37, 521–527 (2008).

    Article  CAS  Google Scholar 

  18. Gonzalez, A., Nave, C. & Marvin, D.A. Pf1 filamentous bacteriophage: refinement of a molecular model by simulated annealing using 3.3 Å resolution X-ray fibre diffraction data. Acta Crystallogr. D Biol. Crystallogr. 51, 792–804 (1995).

    Article  CAS  Google Scholar 

  19. Das, R. et al. Simultaneous prediction of protein folding and docking at high resolution. Proc. Natl. Acad. Sci. USA 106, 18978–18983 (2009).

    Article  CAS  Google Scholar 

  20. Zeri, A.C., Mesleh, M.F., Nevzorov, A.A. & Opella, S.J. Structure of the coat protein in fd filamentous bacteriophage particles determined by solid-state NMR spectroscopy. Proc. Natl. Acad. Sci. USA 100, 6458–6463 (2003).

    Article  CAS  Google Scholar 

  21. Tewary, S.K. et al. Structure of hibiscus latent Singapore virus by fiber diffraction: a nonconserved His122 contributes to coat protein stability. J. Mol. Biol. 406, 516–526 (2011).

    Article  CAS  Google Scholar 

  22. André, I., Bradley, P., Wang, C. & Baker, D. Prediction of the structure of symmetrical protein assemblies. Proc. Natl. Acad. Sci. USA 104, 17656–17661 (2007).

    Article  Google Scholar 

  23. Conway, P., Tyka, M.D., DiMaio, F., Konerding, D.E. & Baker, D. Relaxation of backbone bond geometry improves protein energy landscape modeling. Protein Sci. 23, 47–55 (2014).

    Article  CAS  Google Scholar 

  24. Song, Y. et al. High-resolution comparative modeling with RosettaCM. Structure 21, 1735–1742 (2013).

    Article  CAS  Google Scholar 

  25. Habeck, M., Rieping, W. & Nilges, M. Weighting of experimental evidence in macromolecular structure determination. Proc. Natl. Acad. Sci. USA 103, 1756–1761 (2006).

    Article  CAS  Google Scholar 

  26. Beese, L., Stubbs, G. & Cohen, C. Microtubule structure at 18 Å resolution. J. Mol. Biol. 194, 257–264 (1987).

    Article  CAS  Google Scholar 

  27. Nambudripad, R., Stark, W. & Makowski, L. Neutron diffraction studies of the structure of filamentous bacteriophage Pf1. J. Mol. Biol. 220, 359–379 (1991).

    Article  CAS  Google Scholar 

  28. Brown, P.J., Fox, A.G., Maslen, E.N., O'Keefe, M.A. & Willis, B.T.M. in International Tables for Crystallography Vol. C (ed. Prince, E.) Ch. 6.1, 554–595 (International Union of Crystallography, 2006).

  29. Keiner, J., Kunis, S. & Potts, D. Using NFFT 3—a software library for various nonequispaced fast Fourier transforms. ACM Trans. Math. Softw. 36, 19 (2009).

    Article  Google Scholar 

  30. Siegman, A.E. Quasi fast Hankel transform. Opt. Lett. 1, 13 (1977).

    Article  CAS  Google Scholar 

  31. DiMaio, F., Tyka, M.D., Baker, M.L., Chiu, W. & Baker, D. Refinement of protein structures into low-resolution density maps using Rosetta. J. Mol. Biol. 392, 181–190 (2009).

    Article  CAS  Google Scholar 

  32. Abe, H., Braun, W., Noguti, T. & Gō´, N. Rapid calculation of first and second derivatives of conformational energy with respect to dihedral angles for proteins general recurrent equations. Comput. Chem. 8, 239–247 (1984).

    Article  CAS  Google Scholar 

  33. Wedemeyer, W.J. & Baker, D. Efficient minimization of angle-dependent potentials for polypeptides in internal coordinates. Proteins 53, 262–272 (2003).

    Article  CAS  Google Scholar 

  34. Rambo, R.P. & Tainer, J.A. Accurate assessment of mass, models and resolution by small-angle scattering. Nature 496, 477–481 (2013).

    Article  CAS  Google Scholar 

  35. DiMaio, F., Leaver-Fay, A., Bradley, P., Baker, D. & André, I. Modeling symmetric macromolecular structures in Rosetta3. PLoS ONE 6, e20450 (2011).

    Article  CAS  Google Scholar 

  36. Gront, D., Kulp, D.W., Vernon, R.M., Strauss, C.E.M. & Baker, D. Generalized fragment picking in Rosetta: design, protocols and applications. PLoS ONE 6, e23294 (2011).

    Article  CAS  Google Scholar 

Download references

Acknowledgements

This work was supported by the Crafoord Foundation and the Sven and Lilly Lawski Foundation. The simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc. We thank S.K. Tewary (University of Kansas) for sharing fiber diffraction data of HLSV and input files for X-PLOR simulations. We thank S. Bjelic, S. Rämisch and R. Lizatovic for critically reading the manuscript.

Author information

Authors and Affiliations

  1. Department of Biochemistry and Structural Biology, Lund University, Lund, Sweden

    Wojciech Potrzebowski & Ingemar André

Authors
  1. Wojciech Potrzebowski
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ingemar André
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

W.P. and I.A. designed the research, developed the methods and analyzed the data. W.P. carried out the simulations. W.P. and I.A. wrote the manuscript.

Corresponding authors

Correspondence to Wojciech Potrzebowski or Ingemar André.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Integrated supplementary information

Supplementary Figure 1 Comparison between observed and calculated intensities.

For non-crystalline systems experimental fiber diffraction data (black) is confined to layer lines. Each layer is spaced along meridional direction at Z=l/c, where l is the layer line number and c is helical repeat; and sampled along the equator at an interval of R=0.0025 1/Å. Intensities were calculated from atomic coordinates in reciprocal space (blue, equation 5).

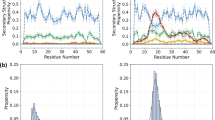
Supplementary Figure 2 Determining structures of bacteriophage viruses de novo with and without experimental data.

We ran Fold-And-Dock simulations guided by fiber diffraction data (blue) and in the absence of experimental data (green). The comparison is shown for: (a) Pf3 filamentous bacteriophage (PDB code: 1ifp), (b) filamentous bacteriophage PH75 (PDB code: 1hgv), (c) filamentous bacteriophage Pf1 (PDB code: 1ql1), (d) filamentous bacteriophage Pf1 (PDB code: 4ifm) and (e) fd filamentous bacteriophage (PDB code: 2c0w). (f) Additionally, fd filamentous bacteriophage (PDB code: 2c0x) simulations were guided by multiple experimental data sets (fiber diffraction and solid state NMR). Models generated without fiber diffraction were validated against work set with the Rosetta score application.

Supplementary Figure 3 Coarse-grained symmetrical docking of HLSV.

Coarse-grained symmetrical docking of (a) the monomeric structure of hibiscus latent Singapore virus (PDB code: 3pdm) and (b) the homology model based on the monomer of tobacco mosaic virus (PDB code: 2tmv). Blue dots corresponds to models obtained from docking guided by fiber diffraction data, while green for models generated without experimental restraints.

Supplementary Figure 4 CPU and GPU performance on calculations of all-atom intensity and derivatives.

All-atom intensity (equation 5) and derivatives (equations S5-S8) can be calculated sequentially using standard CPU or in parallel mode on a Graphical Processor Unit (GPU). We use a structure of hibiscus latent Singapore virus (HLSV) to compare the performance on both architectures. Monomer of HLSV has 162 amino-acid residues and was truncated by factor of 20 to perform calculations on models that consisted of 82, 102, 122 and 142 amino acid residues.

Supplementary information

Supplementary Text and Figures

Supplementary Figures 1–4, Supplementary Table 1, Supplementary Notes 1 and 2 and Supplementary Protocol (PDF 1655 kb)

Supplementary Data 1

Protein models (ZIP 11329 kb)

Supplementary Data 2

Command files for running fiber diffraction modeling with Rosetta (ZIP 28624 kb)

Source data

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Potrzebowski, W., André, I. Automated determination of fibrillar structures by simultaneous model building and fiber diffraction refinement. Nat Methods 12, 679–684 (2015). https://doi.org/10.1038/nmeth.3399

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nmeth.3399

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing