Extracting intracellular diffusive states and transition rates from single-molecule tracking data

Nature Methods volume 10, pages265–269(2013)Cite this article

Subjects

Abstract

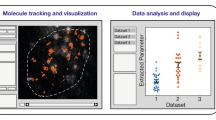
We provide an analytical tool based on a variational Bayesian treatment of hidden Markov models to combine the information from thousands of short single-molecule trajectories of intracellularly diffusing proteins. The method identifies the number of diffusive states and the state transition rates. Using this method we have created an objective interaction map for Hfq, a protein that mediates interactions between small regulatory RNAs and their mRNA targets.

Access options

Rent or Buy article

Get time limited or full article access on ReadCube.

from$8.99

Rent or Buy

All prices are NET prices.

Figure 1: A test of the vbSPT approach using simulated data.
Figure 2: Convergence properties for the model presented in Figure 1 with localization error (σ) of 20 nm.
Figure 3: Test of vbSPT on synthetic data with a spatially varying diffusion constant in a cell geometry.
Figure 4: vbSPT analysis of experimental tracking data on Hfq.

Accession codes

Accessions

Swiss-Prot

References

  1. 1

    Manley, S. et al. High-density mapping of single-molecule trajectories with photoactivated localization microscopy. Nat. Methods 5, 155–157 (2008).

    CAS  Article  Google Scholar 

  2. 2

    Niu, L. & Yu, J. Investigating intracellular dynamics of FtsZ cytoskeleton with photoactivation single-molecule tracking. Biophys. J. 95, 2009–2016 (2008).

    CAS  Article  Google Scholar 

  3. 3

    English, B.P. et al. Single-molecule investigations of the stringent response machinery in living bacterial cells. Proc. Natl. Acad. Sci. USA 108, E365–E373 (2011).

    CAS  Article  Google Scholar 

  4. 4

    Bakshi, S., Siryaporn, A., Goulian, M. & Weisshaar, J.C. Superresolution imaging of ribosomes and RNA polymerase in live Escherichia coli cells. Mol. Microbiol. 85, 21–38 (2012).

    CAS  Article  Google Scholar 

  5. 5

    Bronson, J.E., Fei, J., Hofman, J.M., Gonzalez, R.L. Jr. & Wiggins, C.H. Learning rates and states from biophysical time series: a Bayesian approach to model selection and single-molecule FRET data. Biophys. J. 97, 3196–3205 (2009).

    CAS  Article  Google Scholar 

  6. 6

    Bishop, C.M. Pattern Recognition and Machine Learning (Springer, 2006).

  7. 7

    Das, R., Cairo, C.W. & Coombs, D. A hidden Markov model for single particle tracks quantifies dynamic interactions between LFA-1 and the actin cytoskeleton. PLoS Comput. Biol. 5, e1000556 (2009).

    Article  Google Scholar 

  8. 8

    Chung, I. et al. Spatial control of EGF receptor activation by reversible dimerization on living cells. Nature 464, 783–787 (2010).

    CAS  Article  Google Scholar 

  9. 9

    Beausang, J.F. et al. DNA looping kinetics analyzed using diffusive hidden Markov model. Biophys. J. 92, L64–L66 (2007).

    CAS  Article  Google Scholar 

  10. 10

    Mahmutovic, A., Fange, D., Berg, O.G. & Elf, J. Lost in presumption: stochastic reactions in spatial models. Nat. Methods 9, 1163–1166 (2012).

    CAS  Article  Google Scholar 

  11. 11

    Vogel, J. & Luisi, B.F. Hfq and its constellation of RNA. Nat. Rev. Microbiol. 9, 578–589 (2011).

    CAS  Article  Google Scholar 

  12. 12

    Waters, L.S. & Storz, G. Regulatory RNAs in bacteria. Cell 136, 615–628 (2009).

    CAS  Article  Google Scholar 

  13. 13

    Efron, B. Bootstrap methods: another look at the jackknife. Ann. Stat. 7, 1–26 (1979).

    Article  Google Scholar 

  14. 14

    Link, T.M., Valentin-Hansen, P. & Brennan, R.G. Structure of Escherichia coli Hfq bound to polyriboadenylate RNA. Proc. Natl. Acad. Sci. USA 106, 19292–19297 (2009).

    CAS  Article  Google Scholar 

  15. 15

    Fender, A., Elf, J., Hampel, K., Zimmermann, B. & Wagner, E.G. RNAs actively cycle on the Sm-like protein Hfq. Genes Dev. 24, 2621–2626 (2010).

    CAS  Article  Google Scholar 

  16. 16

    MacKay, D.J.C. Information Theory, Inference, and Learning Algorithms (Cambridge University Press, 2003).

  17. 17

    Bronson, J.E., Hofman, J.M., Fei, J., Gonzalez, R.L. Jr. & Wiggins, C.H. Graphical models for inferring single molecule dynamics. BMC Bioinformatics 11 (suppl. 8), S2 (2010).

    Article  Google Scholar 

  18. 18

    MacKay, D.J.C. Ensemble learning for hidden Markov models. 〈http://www.inference.phy.cam.ac.uk/mackay/abstracts/ensemblePaper.html〉 (1997).

  19. 19

    Ghahramani, Z. An introduction to hidden Markov models and Bayesian networks. in Hidden Markov Models: Applications in Computer Vision (eds. Bunke, H. & Caelli, T.) 9–42 (World Scientific, River Edge, New Jersey, USA, 2001).

  20. 20

    Beal, M.J. Variational Algorithms for Approximate Bayesian Inference. PhD thesis, Univ. College London (2003).

  21. 21

    Okamoto, K. & Sako, Y. Variational Bayes analysis of a photon-based hidden Markov model for single-molecule FRET trajectories. Biophys. J. 103, 1315–1324 (2012).

    CAS  Article  Google Scholar 

  22. 22

    Eddy, S.R. What is Bayesian statistics? Nat. Biotechnol. 22, 1177–1178 (2004).

    CAS  Article  Google Scholar 

  23. 23

    Green, P.J. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika 82, 711–732 (1995).

    Article  Google Scholar 

  24. 24

    Robert, C.P., Rydén, T. & Titterington, D.M. Bayesian inference in hidden Markov models through the reversible jump Markov chain Monte Carlo method. J. R. Stat. Soc., B 62, 57–75 (2000).

    Article  Google Scholar 

Download references

Acknowledgements

We thank I. Barkefors for her careful and critical reading of the manuscript. M.L. is grateful to C.H. Wiggins and J.-W. van de Meent for insightful discussions. This work was supported by the European Research Council (J.E.), the Knut and Alice Wallenberg Foundation (J.E.), Vetenskapsrådet (J.E.), the Göran Gustafsson Foundation (J.E.), the Wenner-Gren Foundations (M.L.) and the Center for Biomembrane Research (M.L.).

Author information

Author notes

  1. Fredrik Persson and Martin Lindén: These authors contributed equally to this work.

Affiliations

  1. Department of Cell and Molecular Biology, Science for Life Laboratory, Uppsala University, Uppsala, Sweden

    Fredrik Persson, Cecilia Unoson & Johan Elf

  2. Department of Biochemistry and Biophysics, Center for Biomembrane Research, Stockholm University, Stockholm, Sweden

    Martin Lindén

Authors
  1. Fredrik Persson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Martin Lindén
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Cecilia Unoson
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Johan Elf
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.E. and M.L. conceived the method, M.L. designed the vbSPT algorithm, M.L. and F.P. implemented and tested the algorithm, F.P. designed and implemented the image analysis and particle-tracking algorithms, and C.U. cloned and characterized the bacterial strains. F.P. and J.E. built the optical setup. F.P., C.U. and J.E. designed the experiments, and C.U. and F.P. performed the experiments. F.P., M.L., C.U. and J.E. wrote the manuscript.

Corresponding author

Correspondence to Johan Elf.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Text and Figures

Supplementary Tables 1–7 and Supplementary Notes 1–5 (PDF 1053 kb)

Supplementary Software

vbSPT (variational Bayes single-particle tracking) software (ZIP 6389 kb)

Rights and permissions

Reprints and Permissions

About this article

Cite this article

Persson, F., Lindén, M., Unoson, C. et al. Extracting intracellular diffusive states and transition rates from single-molecule tracking data. Nat Methods 10, 265–269 (2013). https://doi.org/10.1038/nmeth.2367

Download citation

Further reading

Search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing