Abstract
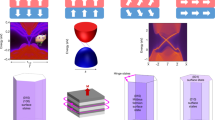
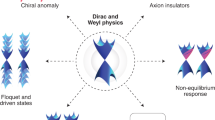
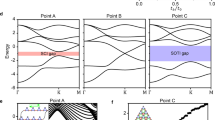
Topological states of quantum matter have been investigated intensively in recent years in materials science and condensed matter physics. The field developed explosively largely because of the precise theoretical predictions, well-controlled materials processing, and novel characterization techniques. In this Perspective, we review recent progress in topological insulators, the quantum anomalous Hall effect, chiral topological superconductors, helical topological superconductors and Weyl semimetals.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
von Klitzing, K., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Laughlin, R. B. Quantized Hall conductivity in two dimensions. Phys. Rev. B 23, 5632–5633 (1981).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Bernevig, B. A. & Zhang, S.-C. Quantum spin Hall effect. Phys. Rev. Lett. 96, 106802 (2006).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306 (2007).
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Roy, R. Topological phases and the quantum spin Hall effect in three dimensions. Phys. Rev. B 79, 195322 (2009).
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the “parity anomaly”. Phys. Rev. Lett. 61, 2015–2018 (1988).
Qi, X.-L., Wu, Y.-S. & Zhang, S.-C. Topological quantization of the spin Hall effect in two-dimensional paramagnetic semiconductors. Phys. Rev. B 74, 085308 (2006).
Liu, C.-X., Qi, X.-L., Dai, X., Fang, Z. & Zhang, S.-C. Quantum anomalous Hall effect in Hg1−yMnyTe quantum wells. Phys. Rev. Lett. 101, 146802 (2008).
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Read, N. & Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 61, 10267–10297 (2000).
Ivanov, D. A. Non-abelian statistics of half-quantum vortices in p-wave superconductors. Phys. Rev. Lett. 86, 268–271 (2001).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Qi, X.-L., Hughes, T. L., Raghu, S. & Zhang, S.-C. Time-reversal-invariant topological superconductors and superfluids in two and three dimensions. Phys. Rev. Lett. 102, 187001 (2009).
Schnyder, A. P., Ryu, S., Furusaki, A. & Ludwig, A. W. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
Kitaev, A. Periodic table for topological insulators and superconductors. AIP Conf. Proc. 1134, 22 (2009).
Roth, A. et al. Nonlocal transport in the quantum spin Hall state. Science 325, 294–297 (2009).
Hart, S. et al. Induced superconductivity in the quantum spin Hall edge. Nat. Phys. 10, 638–643 (2014).
Liu, C., Hughes, T. L., Qi, X.-L., Wang, K. & Zhang, S.-C. Quantum spin Hall effect in inverted type-II semiconductors. Phys. Rev. Lett. 100, 236601 (2008).
Knez, I. et al. Observation of edge transport in the disordered regime of topologically insulating InAs/GaSb quantum wells. Phys. Rev. Lett. 112, 026602 (2014).
Du, L., Knez, I., Sullivan, G. & Du, R.-R. Robust helical edge transport in gated InAs/GaSb bilayers. Phys. Rev. Lett. 114, 096802 (2015).
Spanton, E. M. et al. Images of edge current in InAs/GaSb quantum wells. Phys. Rev. Lett. 113, 026804 (2014).
Pribiag, V. S. et al. Edge-mode superconductivity in a two-dimensional topological insulator. Nat. Nanotech. 10, 593–597 (2015).
Li, T. et al. Low temperature conductivity of weakly interacting quantum spin Hall edges in strained-Layer InAs/GaInSb. Preprint at http://arXiv.org/abs/1707.09024 (2017).
Xu, Y. et al. Large-gap quantum spin Hall insulators in tin films. Phys. Rev. Lett. 111, 136804 (2013).
Zhu, F. et al. Epitaxial growth of two-dimensional stanene. Nat. Mat. 14, 1020–1025 (2015).
Qian, X., Liu, J., Fu, L. & Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science 346, 1344–1347 (2014).
Fei, Z. et al. Edge conduction in monolayer WTe2 . Nat. Phys. 13, 677–682 (2017).
Liu, Q., Liu, C.-X., Xu, C., Qi, X.-L. & Zhang, S.-C. Magnetic impurities on the surface of a topological insulator. Phys. Rev. Lett. 102, 156603 (2009).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Chang, C.-Z. et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 14, 473–477 (2015).
Mogi, M. et al. Magnetic modulation doping in topological insulators toward higher-temperature quantum anomalous Hall effect. Appl. Phys. Lett. 107, 182401 (2015).
Wang, J., Lian, B. & Zhang, S.-C. Universal scaling of the quantum anomalous Hall plateau transition. Phys. Rev. B 89, 085106 (2014).
Kou, X. et al. Metal-to-insulator switching in quantum anomalous Hall states. Nat. Commun. 6, 8474 (2015).
Feng, Y. et al. Observation of the zero Hall plateau in a quantum anomalous Hall insulator. Phys. Rev. Lett. 115, 126801 (2015).
Mogi, M. et al. A magnetic heterostructure of topological insulators as a candidate for an axion insulator. Nat. Mater. 16, 516–521 (2017).
Wang, J., Lian, B., Qi, X.-L. & Zhang, S.-C. Quantized topological magnetoelectric effect of the zero-plateau quantum anomalous Hall state. Phys. Rev. B 92, 081107 (2015).
Essin, A. M., Moore, J. E. & Vanderbilt, D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys. Rev. Lett. 102, 146805 (2009).
Okada, K. N. et al. Terahertz spectroscopy on Faraday and Kerr rotations in a quantum anomalous Hall state. Nat. Commun. 7, 12245 (2016).
Wu, L. et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 354, 1124–1127 (2016).
Dziom, V. et al. Observation of the universal magnetoelectric effect in a 3D topological insulator. Nat. Commun. 8, 15197 (2017).
Mackenzie, A. P. & Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 75, 657–712 (2003).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Chiral topological superconductor from the quantum Hall state. Phys. Rev. B 82, 184516 (2010).
Wang, J., Zhou, Q., Lian, B. & Zhang, S.-C. Chiral topological superconductor and half-integer conductance plateau from quantum anomalous Hall plateau transition. Phys. Rev. B 92, 064520 (2015).
Chung, S. B., Qi, X.-L., Maciejko, J. & Zhang, S.-C. Conductance and noise signatures of Majorana backscattering. Phys. Rev. B 83, 100512 (2011).
He, Q. L. et al. Chiral Majorana fermion modes in a quantum anomalous Hall insulator–superconductor structure. Science 357, 294–299 (2017).
Fu, L. & Kane, C. L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Wang, Z. et al. Topological nature of the FeSe0.5Te0.5 superconductor. Phys. Rev. B 92, 115119 (2015).
Xu, G., Lian, B., Tang, P., Qi, X.-L. & Zhang, S.-C. Topological superconductivity on the surface of Fe-based superconductors. Phys. Rev. Lett. 117, 047001 (2016).
Zhang, P. et al. Observation of topological superconductivity on the surface of iron-based superconductor. Preprint at http://arXiv.org/abs/1706.05163 (2017).
Wang, D. et al. Observation of pristine Majorana bound state in iron-based superconductor. Preprint at http://arXiv.org/abs/1706.06074 (2017).
Hasan, M. Z., Xu, S.-Y., Belopolski, I. & Huang, S.-M. Discovery of Weyl fermion semimetals and topological Fermi arc states. Annu. Rev. Con. Mat. Phys. 8, 289–309 (2017).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three dimensional solids. Rev. Mod. Phys. Preprint at http://arXiv.org/abs/1705.01111 (in the press, 2017).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Ruan, J. et al. Symmetry-protected ideal Weyl semimetal in HgTe-class materials. Nat. Commun. 7, 11136 (2016).
Bulmash, D., Liu, C.-X. & Qi, X.-L. Prediction of a Weyl semimetal in Hg1−x−yCdxMnyTe. Phys. Rev. B 89, 081106 (2014).
König, M. et al. The quantum spin Hall effect: theory and experiment. J. Phys. Soc. Jpn 77, 031007 (2008).
Acknowledgements
J.W. acknowledges support from the Natural Science Foundation of China through Grant No. 11774065, the Natural Science Foundation of Shanghai under Grant No. 17ZR1442500 and the National Thousand-Young-Talents Program. S.-C.Z. is supported by the Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering, under contract DE-AC02-76SF00515.
Author information
Authors and Affiliations
Contributions
The Perspective reported here emerged from lively discussions between the authors. All authors contributed to writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Wang, J., Zhang, SC. Topological states of condensed matter. Nature Mater 16, 1062–1067 (2017). https://doi.org/10.1038/nmat5012
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat5012
This article is cited by
-
Spin effects on transport and zero-bias anomaly in a hybrid Majorana wire-quantum dot system
Scientific Reports (2023)
-
Experimental observation of Berry phases in optical Möbius-strip microcavities
Nature Photonics (2023)
-
Thermoelectric properties of topological chains coupled to a quantum dot
Scientific Reports (2023)
-
Topologically enhanced nonlinear optical response of graphene nanoribbon heterojunctions
Quantum Frontiers (2023)
-
Low-temperature magnetic crossover in the topological kagome magnet TbMn6Sn6
Communications Physics (2022)