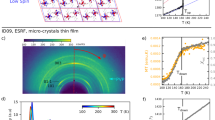
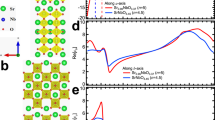
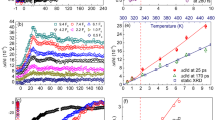
Abstract
Photoinduced phase transitions are of special interest in condensed matter physics1,2 because they can be used to change complex macroscopic material properties on the ultrafast timescale. Cooperative interactions between microscopic degrees of freedom greatly enhance the number and nature of accessible states, making it possible to switch electronic, magnetic or structural properties in new ways2,3,4,5,6,7,8,9. Photons with high energies, of the order of electron volts, in particular are able to access electronic states that may differ greatly from states produced with stimuli close to equilibrium10. In this study we report the photoinduced change in the lattice structure of a charge and orbitally ordered Nd0.5Sr0.5MnO3 thin film using picosecond time-resolved X-ray diffraction. The photoinduced state is structurally ordered, homogeneous, metastable and has crystallographic parameters different from any thermodynamically accessible state. A femtosecond time-resolved spectroscopic study shows the formation of an electronic gap in this state. In addition, the threshold-like behaviour and high efficiency in photo-generation yield of this gapped state highlight the important role of cooperative interactions in the formation process. These combined observations point towards a ‘hidden insulating phase’ distinct from that found in the hitherto known phase diagram.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Tokura, Y. Photoinduced phase transition: A tool for generating a hidden state of matter. J. Phys. Soc. Jpn 75, 011001 (2006).
Nasu, K. Photoinduced Phase Transitions (World Scientific, 2004).
Vahaplar, K. et al. Ultrafast path for optical magnetization reversal via a strongly nonequilibrium state. Phys. Rev. Lett. 103, 117201 (2009).
Lorenc, M. et al. Successive dynamical steps of photoinduced switching of a molecular Fe(III) spin-crossover material by time-resolved X-ray diffraction. Phys. Rev. Lett. 103, 028301 (2009).
Rini, M. et al. Control of the electronic phase of a manganite by mode-selective vibrational excitation. Nature 449, 72–74 (2007).
Collet, E. et al. Laser-induced ferroelectric structural order in an organic charge-transfer crystal. Science 300, 612–615 (2003).
Cavalleri, A., Rini, M & Schoenlein, R. W. Ultra-broadband femtosecond measurements of the photo-induced phase transition in VO2: From the mid-IR to the hard X-rays. J. Phys. Soc. Jpn 75, 011004 (2006).
Kolobov, A. V. et al. Understanding the phase-change mechanism of rewritable optical media. Nature Mater. 3, 703–708 (2004).
Koshihara, S. & Adachi, S. Photo-induced phase transition in an electron–lattice correlated system—future role of a time-resolved X-ray measurement for materials science. J. Phys. Soc. Jpn 75, 011005 (2006).
Huai, P. & Nasu, K. Difference between photoinduced phase and thermally excited phase. J. Phys. Soc. Jpn 71, 1182–1188 (2002).
Kajimoto, R. et al. Hole-concentration-induced transformation of the magnetic and orbital structures in Nd1−xSrxMnO3 . Phys. Rev. B 60, 9506–9517 (1999).
Okuyama, D. et al. Lattice-form-dependent orbital shape and charge disproportionation in charge- and orbital-ordered manganites. Phys. Rev. B 80, 064402 (2009).
Tobe, K., Kimura, T. & Tokura, Y. Anisotropic optical spectra of doped manganites with pseudocubic perovskite structure. Phys. Rev. B 69, 014407 (2004).
Ogimoto, Y. et al. Strain-induced crossover of the metal–insulator transition in perovskite manganites. Phys. Rev. B 71, 060403(R) (2005).
Nakamura, M., Ogimoto, Y., Tamaru, H., Izumi, M. & Miyano, K. Phase control through anisotropic strain in Nd0.5Sr0.5MnO3 thin films. Appl. Phys. Lett. 86, 182504 (2005).
Miyasaka, K., Nakamura, M., Ogimoto, Y., Tamaru, H. & Miyano, K. Ultrafast photoinduced magnetic moment in a charge–orbital-ordered antiferromagnetic Nd0.5Sr0.5MnO3 thin film. Phys. Rev. B 74, 012401 (2006).
Wakabayashi, Y. et al. Size of orbital-ordering domain controlled by the itinerancy of the 3d electrons in a manganite thin film. Phys. Rev. B 79, 220403(R) (2009).
Wakabayashi, Y. et al. Orbital ordering structures in (Nd,Pr)0.5Sr0.5MnO3 manganite thin films on perovskite (011) substrates. J. Phys. Soc. Jpn 77, 014712 (2008).
Anisimov, V. I., Elfimov, I. S., Korotin, M. A. & Terakura, K. Orbital and charge ordering in Pr1−xCaxMnO3 (x=0 and 0.5) from the ab initio calculations. Phys. Rev. B 55, 15494–15499 (1997).
Maezono, R., Ishihara, S. & Nagaosa, N. Phase diagram of manganese oxides. Phys. Rev. B 58, 11583–11596 (1998).
Yunoki, S., Hotta, T. & Dagotto, E. Ferromagnetic, A-type, and charge-ordered CE-type states in doped manganites using Jahn–Teller phonons. Phys. Rev. Lett. 84, 3714–3717 (2000).
Ebata, K., Mizokawa, T. & Fujimori, A. Orbital ordering in La0.5Sr1.5MnO4 studied by model Hartree–Fock calculation. Phys. Rev. B 72, 233104 (2005).
Miyano, K., Tanaka, T., Tomioka, Y. & Tokura, Y. Photoinduced insulator-to-metal transition in a perovskite manganite. Phys. Rev. Lett. 78, 4257–4260 (1997).
Dagotto, E. Springer Series in Solid-State Sciences 136 (Springer, 2003).
Matsubara, M. et al. Key for photoinduced insulator–metal transitions in manganites; lattice constant matching between charge/orbital ordered insulator and ferromagnetic metal. J. Phys. Soc. Jpn 78, 023707 (2009).
Tamaru, H., Ishida, K, Ogawa, N., Kubo, Y. & Miyano, K. Pump-and-probe study in LaMnO3 thin films. Phys. Rev. B 78, 075119 (2008).
Polli, D. et al. Coherent orbital waves in the photo-induced insulator–metal dynamics of a magnetoresistive manganite. Nature Mater. 6, 643–647 (2007).
Satoh, K. & Ishihara, S. Photo-induced phase transition in charge ordered perovskite manganites. J. Magn. Magn. Mater. 310, 798–800 (2007).
Kanamori, Y., Matsueda, H. & Ishihara, S. Dynamical coupling and separation of multiple degrees of freedom in a photoexcited double-exchange system. Phys. Rev. Lett. 103, 267401 (2009).
Beaud, P. et al. Ultrafast structural phase transition driven by photoinduced melting of charge and orbital order. Phys. Rev. Lett. 103, 155702 (2009).
Acknowledgements
This work was partially supported by Grant-in-Aids for Scientific Research from the MEXT, Japan, and the G-COE programme for chemistry in Tokyo Institute of Technology. This work was carried out with the approval of the Photon Factory Program Advisory Committee (Proposal No. 2004S1-001). The authors thank Y. Okimoto (Tokyo Institute of Technology) for fruitful discussions.
Author information
Authors and Affiliations
Contributions
Sample preparation and optical measurements were carried out by Y.O., M.N., R.T. and K.M. H.I. planned the X-ray measurements and carried out the experiment and analysis. S.N., S-i.A., T-h.A. and H.S. planned, conducted and analysed the X-ray measurements; in addition, T.S., A.T., K.I., M.C. and L.G. assisted with the X-ray measurements. N.D. also assisted with the X-ray experiment under the supervision of A.C., as part of the G-COE student exchange program. All authors discussed the results and contributed to the manuscript. S-y.K. and K.M. initiated and oversaw the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1314 kb)
Supplementary Video
Supplementary Video (MPG 5689 kb)
Rights and permissions
About this article
Cite this article
Ichikawa, H., Nozawa, S., Sato, T. et al. Transient photoinduced ‘hidden’ phase in a manganite. Nature Mater 10, 101–105 (2011). https://doi.org/10.1038/nmat2929
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat2929
This article is cited by
-
Ultrafast and persistent photoinduced phase transition at room temperature monitored by streaming powder diffraction
Nature Communications (2024)
-
A coherent phonon-induced hidden quadrupolar ordered state in Ca2RuO4
Nature Communications (2023)
-
Terahertz control of many-body dynamics in quantum materials
Nature Reviews Materials (2023)
-
Atomic-scale view of the photoinduced structural transition to form sp3-like bonded order phase in graphite
Scientific Reports (2023)
-
Toward fully automated UED operation using two-stage machine learning model
Scientific Reports (2022)