Abstract
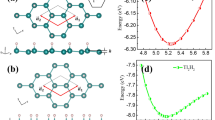
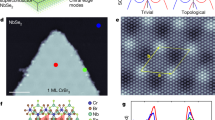
Recently the quantum spin Hall effect was theoretically predicted and experimentally realized in quantum wells based on the binary semiconductor HgTe (refs 1–3). The quantum spin Hall state and topological insulators are new states of quantum matter interesting for both fundamental condensed-matter physics and material science1,2,3,4,5,6,7,8,9,10,11. Many Heusler compounds with C1b structure are ternary semiconductors that are structurally and electronically related to the binary semiconductors. The diversity of Heusler materials opens wide possibilities for tuning the bandgap and setting the desired band inversion by choosing compounds with appropriate hybridization strength (by the lattice parameter) and magnitude of spin–orbit coupling (by the atomic charge). Based on first-principle calculations we demonstrate that around 50 Heusler compounds show band inversion similar to that of HgTe. The topological state in these zero-gap semiconductors can be created by applying strain or by designing an appropriate quantum-well structure, similar to the case of HgTe. Many of these ternary zero-gap semiconductors (LnAuPb, LnPdBi, LnPtSb and LnPtBi) contain the rare-earth element Ln, which can realize additional properties ranging from superconductivity (for example LaPtBi; ref. 12) to magnetism (for example GdPtBi; ref. 13) and heavy fermion behaviour (for example YbPtBi; ref. 14). These properties can open new research directions in realizing the quantized anomalous Hall effect and topological superconductors.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Bernevig, B. A., Hughes, T. L. & Zhang, S. C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Dai, X. et al. Helical edge and surface states in HgTe quantum wells and bulk insulators. Phys. Rev. B 77, 125319 (2008).
Qi, X-L. & Zhang, S-C. The quantum spin Hall effect and topological insulators. Phys. Today 63, 33–38 (2010).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Bernevig, B. A. & Zhang, S. C. Quantum spin Hall effect. Phys. Rev. Lett. 96, 106802 (2006).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Hsieh, D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–974 (2008).
Zhang, H. et al. Topological insulators in Bi2Se3,Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nature Phys. 5, 438–442 (2009).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nature Phys. 5, 398–402 (2009).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3 . Science 325, 178–181 (2009).
Goll, G. et al. Thermodynamic and transport properties of the noncentrosymmetric superconductor LaBiPt. Physica B 403, 1065–1067 (2008).
Canfield, P. C. et al. Magnetism and heavy fermion-like behavior in the RBiPt series. J. Appl. Phys. 70, 5800–5802 (1991).
Fisk, Z. et al. Massive electron state in YbBiPt. Phys. Rev. Lett. 67, 3310–3313 (1991).
Villars, P. & Calvert, L. D. Pearson’s Handbook of Crystallographic Data for Intermetallic Phases (Amer Soc Metals, 1991).
Qi, X-L., Li, R., Zang, J. & Zhang, S-C. Inducing a magnetic monopole with topological surface states. Science 323, 1184–1187 (2009).
Li, R., Wang, J., Qi, X-L. & Zhang, S-C. Dynamical axion field in topological magnetic insulators. Nature Phys. 6, 284–288 (2010).
Fu, L. & Kane, C. L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Felser, C., Fecher, G. H. & Balke, B. Spintronics: A challenge for materials science and solid-state chemistry. Angew. Chem. Int. Ed. 46, 668–699 (2007).
Galanakis, I., Dederichs, P. H. & Papanikolaou, N. Slater–Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 66, 174429 (2002).
Jung, D., Koo, H. J. & Whangbo, M. H. Study of the 18-electron band gap and ferromagnetism in semi-Heusler compounds by non-spin-polarized electronic band structure calculations. J. Mol. Struct. Theochem. 527, 113–119 (2000).
Galanakis, I., Dederichs, P. H. & Papanikolaou, N. Origin and properties of the gap in the half-ferromagnetic Heusler alloys. Phys. Rev. B 66, 134428 (2002).
Kandpal, H. C., Felser, C. & Seshadri, R. Covalent bonding and the nature of band gaps in some half-Heusler compounds. J. Phys. D 39, 776–785 (2006).
Sakurada, S. & Shutoh, N. Effect of Ti substitution on the thermoelectric properties of (Zr, Hf)NiSn half-Heusler compounds. Appl. Phys. Lett. 86, 082105 (2005).
von Middendorff, A., Kohler, H. & Landwehr, G. Thermoelectric power of n-type Bi2Se3 in strong transverse magnetic-fields. Phys. Status Solidi B 57, 203–210 (1973).
Hor, Y. S. et al. p-type Bi2Se8 for topological insulator and low-temperature thermoelectric application. Phys. Rev. B 79, 195208 (2009).
Vosko, S. H., Wilk, L. & Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 58, 1200–1211 (1980).
Dzero, M., Sun, K., Galitski, V. & Coleman, P. Topological Kondo insulators. Phys. Rev. Lett. 104, 106408 (2010).
Qi, X. L., Hughes, T. & Zhang, S. C. Topological invariants for the Fermi surface of a time-reversal-invariant superconductor. Phys. Rev. B 81, 134508 (2010).
Acknowledgements
We acknowledge C. X. Liu for discussion. This work is supported by ARO, grant number W911NF-09-1-0508. Financial support by the Deutsche Forschungsgemeinschaft (DFG, research unit FOR 559, project P 07) is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the work presented in this Letter.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Chadov, S., Qi, X., Kübler, J. et al. Tunable multifunctional topological insulators in ternary Heusler compounds. Nature Mater 9, 541–545 (2010). https://doi.org/10.1038/nmat2770
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat2770
This article is cited by
-
Exploring the physical properties of Co2MnSi full Heusler alloy: a first principles study
Optical and Quantum Electronics (2024)
-
Top-down patterning of topological surface and edge states using a focused ion beam
Nature Communications (2023)
-
Half-Heusler phase TmNiSb under pressure: intrinsic phase separation, thermoelectric performance and structural transition
Scientific Reports (2023)
-
Colossal negative magnetoresistance in field-induced Weyl semimetal of magnetic half-Heusler compound
Nature Communications (2023)
-
Prediction of the electronic structure, optical and vibrational properties of ScXCo2Sb2 (X = V, Nb and Ta) double half-Heusler alloys: a theoretical study
Indian Journal of Physics (2023)