Abstract
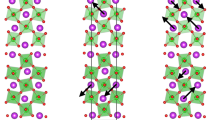
Understanding the ferroelectrocity in magnetic ferroelectric oxides is of both fundamental and technological importance. Here, we identify the nature of the ferroelectric phase transition in the hexagonal manganite, YMnO3, using a combination of single-crystal X-ray diffraction, thorough structure analysis and first-principles density-functional calculations. The ferroelectric phase is characterized by a buckling of the layered MnO5 polyhedra, accompanied by displacements of the Y ions, which lead to a net electric polarization. Our calculations show that the mechanism is driven entirely by electrostatic and size effects, rather than the usual changes in chemical bonding associated with ferroelectric phase transitions in perovskite oxides. As a result, the usual indicators of structural instability, such as anomalies in Born effective charges on the active ions, do not hold. In contrast to the chemically stabilized ferroelectrics, this mechanism for ferroelectricity permits the coexistence of magnetism and ferroelectricity, and so suggests an avenue for designing novel magnetic ferroelectrics.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Auciello, O., Scott, J.F. & Ramesh, R. The physics of ferroelectric memories. Phys. Today 51, 22–27 (1998).
Busch-Vishniac, I.J. Trends in electromechanical transduction. Phys. Today 51, 28–34 (1998).
Fujimura, N., Ishida, T., Yoshimura, T. & Ito, T. Epitaxially grown YMnO3 film: New candidate for nonvolatile memory devices. Appl. Phys. Lett. 69, 1011–1013 (1996).
Ito, D., Fujimura, N., Yoshimura, T. & Ito, T. Ferroelectric properties of YMnO3 epitaxial films for ferroelectric-gate field-effect transistors. J. Appl. Phys. 93, 5563–5567 (2003).
Fiebig, M., Lottermoser, T., Fröhlich, D., Goltsev, A.V. & Pisarev, R.V. Observation of coupled magnetic and electric domains. Nature 419, 818–820 (2002).
Ok, K.M., Bhuvanesh, N.S.P. & Halasyamani, P.S. Bi2TeO5: Synthesis structure and powder second harmonic generation properties. Inorg. Chem. 40, 1978–1980 (2001).
Cohen, R.E. & Krakauer, H. Electronic-structure studies of the differences in ferroelectric behavior of BaTiO3 and PbTiO3 . Ferroelectrics 136, 65–83 (1992).
Cohen, R.E. Origin of ferroelectricity in perovskite oxides. Nature 358, 136–138 (1992).
Hill, N.A. Why are there so few magnetic ferroelectrics? J. Phys. Chem. B 104, 6694–6709 (2000).
Atanasov, M. & Reinen, D. Density functional studies on the lone pair effect of the trivalent group V elements: I. electronic structure, vibronic coupling, and chemical criteria for the occurrence of lone pair distortions in AX3 molecules (A=N to Bi; X=H, and F to I). J. Phys. Chem. A 105, 5450–5467 (2001).
Waghmare, U.V., Spaldin, N.A., Kandpal, H.C. & Seshadri, R. First principles indicators of metallicity and cation off-centricity in the IV-VI rock-salt chalcogenides of divalent Ge, Sn and Pb. Phys. Rev. B 67, 125111 (2003).
Seshadri, R. & Hill, N.A. Visualizing the role of Bi 6s “lone pairs” in the off-center distortion in ferromagnetic BiMnO3 . Chem. Mater. 13, 2892–2899 (2001).
Wang, J. et al. Epitaxial BiFeO3 multiferroic thin film heterostructures. Science 299, 1719–1722 (2003).
Kuroiwa, Y. et al. Evidence for Pb-O covalency in tetragonal PbTiO3 . Phys. Rev. Lett. 87, 217601 (2001).
Jones, G.O. & Thomas, P.A. Investigation of the structure and phase transitions in the novel a-site substituted distorted perovskite compound Na0.5Bi0.5TiO3 . Acta Crystallogr. B 58, 168–178 (2002).
Kimura, T. et al. Magnetic control of ferroelectric polarization. Nature 426, 55–58 (2003).
Glazer, A.M. The classification of tilted octahedra in perovskites. Acta Crystallogr. B 28, 3384–3392 (1972).
Van Aken, B.B., Meetsma, A., Tomioka, Y., Tokura, Y. & Palstra, T.T.M. Structural response to O*-O' and magnetic transitions in orthorhombic perovskites. Phys. Rev. B 66, 224414 (2002).
Van Aken, B.B. Structural Response to Electronic Transitions in Hexagonal and Ortho-manganites Thesis, Univ. Groningen (2001).
Yakel, H.L., Koehler, W.C., Bertaut, E.F. & Forrat, E.F. On the crystal structure of the manganese (III) trioxides of the heavy lanthanide and yttrium. Acta Crystallogr. 16, 957–962 (1963).
Smolenskii, G.A. & Bokov, V.A. Coexistence of magnetic and electric ordering in crystals. J. Appl. Phys. 35, 915–918 (1964).
Bertaut, E.F., Pauthenet, R. & Mercier, M. Proprietes magnetiques et structures du manganite d'yttrium. Phys. Lett. 7, 110–111 (1963).
Bertaut, E.F., Pauthenet, R. & Mercier, M. Sur des proprietes magnetiques du manganite d'yttrium. Phys. Lett. 18, 13 (1965).
Lottermoser, T., Fiebig, M., Fröhlich, D., Kallenbach, S. & Maat, M. Coupling of ferroelectric and antiferromagnetic order parameters in hexagonal RMnO3 . Appl. Phys. B 74, 759–764 (2002).
Lukaszewicz, K. & Karut-Kalicinska, J. X-ray investigations of the crystal structure and phase transitions of YMnO3 . Ferroelectrics 7, 81–82 (1974).
Iliev, M.N. et al. Raman- and infrared-active phonons in hexagonal YMnO3: Experiment and lattice-dynamical calculations. Phys. Rev. B 56, 2488–2494 (1997).
Van Aken, B.B., Meetsma, A. & Palstra, T.T.M. Hexagonal YMnO3 . Acta Crystallogr. C 57, 230–232 (2001).
Van Aken, B.B., Meetsma, A. & Palstra, T.T.M. Hexagonal LuMnO3 revisited. Acta Cryst. E 57, i38–i40 (2001); ibid. i87–i89; ibid. i101–i103.
Muñoz, A. et al. Magnetic structure of hexagonal RMnO3 (R = Y, Sc): thermal evolution from neutron powder diffraction. Phys. Rev. B 62, 9498–9510 (2000).
Katsufuji, T. et al. Crystal structure and magnetic properties of hexagonal RMnO3 (R = Y, Lu and Sc) and the effect of doping. Phys. Rev. B 66, 134434 (2002).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, 864–871 (1964).
Kohn, W. & Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, 1133–1138 (1965).
Filippetti, A. & Spaldin, N.A. Self-interaction corrected pseudopotential scheme for magnetic and strongly-correlated systems. Phys. Rev. B 67, 125109 (2003).
Filippetti, A. & Hill, N.A. Coexistence of magnetism and ferroelectricity in perovskites. Phys. Rev. B 65, 195120 (2002).
Shannon, R.D. & Prewitt, C.T. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A 32, 751–767 (1976).
Zhong, W., King-Smith, R.D. & Vanderbilt, D. Giant LO-TO splittings in perovskite ferroelectrics. Phys. Rev. Lett. 72, 3618–3621 (1994).
Ghosez, P., Michenaud, J.-P. & Gonze, X. Dynamical atomic charges: The case of ABO3 compounds. Phys. Rev. B 58, 6224–6240 (1998).
Resta, R., Posternak, M. & Baldereschi, A. Towards a quantum-theory of polarization in ferroelectrics - the case of KNbO3 . Phys. Rev. Lett. 70, 1010–1013 (1993).
Posternak, M., Resta, R. & Baldereschi, A. Role of covalent bonding in the polarization of perovskite oxides - the case of KNbO3 . Phys. Rev. B 50, 8911–8914 (1994).
Ghosez, P., Gonze, X. & Michenaud, J.-P. First principles calculations of dielectric and effective charge tensors in barium titanate. Ferroelectrics 153, 91–96 (1994).
King-Smith, R.D. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, R1651–R1654 (1993).
Resta, R. Macroscopic electric polarization as a geometric quantum phase. Eur. Phys. Lett. 22, 133–138 (1993).
Resta, R. Macroscopic polarization in crystalline dielectrics: the geometric phase approach. Rev. Mod. Phys. 66, 899–915 (1994).
Lonkai, T. Electric and Magnetic Order Parameter in the Multiferroic Hexagonal RMnO3 System Thesis, Tübingen Univ. (2003).
Tomuta, D. Investigations of Hexagonal Manganites with Magnetic and Non-Magnetic Rare Earths Thesis, Univ. Leiden (2003).
Mizokawa, T., Khomskii, D.I. & Sawatzky, G.A. Interplay between orbital ordering and lattice distortions in LaMnO3, YVO3, and YTiO3 . Phys. Rev. B 60, 7309–7313 (1999).
Abrahams, S.C. Ferroelectricity and structure in the YMnO3 family. Acta Crystallogr. B 57, 485–490 (2001).
Edwardson, P.J. et al. Ferroelectricity in perovskitelike NaCaF3 predicted ab initio. Phys. Rev. B 39, 9738–9741 (1989).
Boyer, L.L. et al. Predicted properties of NaCaF3 . AIP Conf. Proc. 535, 364–371 (2000).
Kozlov, G.V., Volkov, A.A., Scott, J.F., Feldkamp, G. & Petzelt, J. Millimeter-wavelength spectroscopy of the ferroelectric phase transition in tris-sarcosine calcium chloride (CH3NHCH2COOH)3CaCl2 . Phys. Rev. B 28, 255–261 (1983).
Iwata, Y., Shibuya, I., Wada, M., Sawada, A. & Ishibashi, Y. Neutron diffraction study of structural phase transition in ferroelectric Li2Ge7O15 . J. Phys. Soc. Jpn 56, 2420–2427 (1987).
Acknowledgements
We thank Neil Mathur, Jim Scott, Ron Smith and Auke Meetsma for invaluable discussions and experimental assistance. The work by A.F. and N.A.S. on this project was funded by the US National Science Foundation's Division of Materials Research, grant number DMR-0312407. This work is supported by the Stichting voor Fundamenteel Onderzoek der Materie (FOM). Beam time at ISIS Rutherford Appleton Laboratory, Chilton, Didcot, UK was funded by Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO). A.F. acknowledges funding from the Italian Ministry of Research (MIUR) under the Rentro Cervelli 2002 program.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Van Aken, B., Palstra, T., Filippetti, A. et al. The origin of ferroelectricity in magnetoelectric YMnO3. Nature Mater 3, 164–170 (2004). https://doi.org/10.1038/nmat1080
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat1080
This article is cited by
-
Thermal Hall effects due to topological spin fluctuations in YMnO3
Nature Communications (2024)
-
Impact of aliovalent ions doping on structural and electrical characteristics of YMnO3 ceramic
Applied Physics A (2023)
-
Enhanced room temperature ferromagnetism in YMnO3-modified lead-free ferroelectric Bi0.5Na0.5TiO3 materials
Applied Physics A (2023)
-
Influence of substrate-induced strain on exchange bias effect in YSMO/LSMO heterostructures
Bulletin of Materials Science (2023)
-
Direct observation of geometric and sliding ferroelectricity in an amphidynamic crystal
Nature Materials (2022)