Abstract
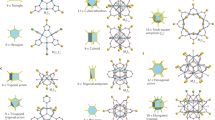
The recognition of quasicrystals, which exhibit long-range order but lack translational symmetry, represented both the introduction of a new class of materials and a transformative breakthrough in crystallography. Concomitant with the exploration of quasicrystallinity, metal–organic architectures emerged as promising and versatile systems with significant application potential. Their building principles have been studied extensively and become manifest in a multitude of intricate amorphous and crystalline phases. To date, however, indications for quasicrystalline order have been elusive in metal–organic coordination networks (MOCNs). Here we employ rare-earth-directed assembly to construct a two-dimensional tiling with quasicrystalline characteristics at a well-defined gold substrate. By careful stoichiometry control over europium centres and functional linkers, we produced a porous network, including the simultaneous expression of four-fold, five-fold and six-fold vertices. The pertaining features were directly inspected by scanning tunnelling microscopy, and the molecule–europium reticulation was recognized as square-triangle tessellation with dodecagonal symmetry. Our findings introduce quasicrystallinity in surface-confined MOCNs with a nanoporous structure and anticipate functionalities that arise from quasicrystalline ordering of the coordinative spheres.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Shechtman, D., Blech, I., Gratias, D. & Cahn, J. W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53, 1951–1953 (1984).
Levine, D. & Steinhardt, P. J. Quasicrystals: a new class of ordered structures. Phys. Rev. Lett. 53, 2477–2480 (1984).
Janssen, T., Chapuis, G. & Boissieu, M. D. Aperiodic Crystals: from Modulated Phases to Quasicrystals (Oxford Univ. Press, 2007).
Steurer, W. & Deloudi, S. Crystallography of Quasicrystals (Springer, 2009).
Baake, M. & Grimm, U. Encyclopedia of Mathematics and Its Applications: Aperiodic Order (Cambridge Univ. Press, 2013).
Poon, S. J. Electronic properties of quasicrystals: an experimental review. Adv. Phys. 41, 303–363 (1992).
Dubois, J.-M. Properties- and applications of quasicrystals and complex metallic alloys. Chem. Soc. Rev. 41, 6760–6777 (2012).
Vardeny, Z. V., Nahata, A. & Agrawal, A. Optics of photonic quasicrystals. Nature Photon. 7, 177–187 (2013).
Deguchi, K. et al. Quantum critical state in a magnetic quasicrystal. Nature Mater. 11, 1013–1016 (2012).
Ishimasa, T., Nissen, H. U. & Fukano, Y. New ordered state between crystalline and amorphous in Ni–Cr particles. Phys. Rev. Lett. 55, 511–513 (1985).
Steurer, W. Twenty years of structure research on quasicrystals. Z. Kristallogr. 219, 391–446 (2004).
Ishimasa, T. Dodecagonal quasicrystals still in progress. Isr. J. Chem. 51, 1216–1225 (2011).
Steurer, W. Why are quasicrystals quasiperiodic? Chem. Soc. Rev. 41, 6719–6729 (2012).
Bindi, L., Steinhardt, P. J., Yao, N. & Lu, P. J. Natural quasicrystals. Science 324, 1306–1309 (2009).
Ishimasa, T. et al. Phason space analysis and structure modeling of 100 Å-scale dodecagonal quasicrystal in Mn-based alloy. Phil. Mag. A 95, 3745–3767 (2015).
Zeng, X. et al. Supramolecular dendritic liquid quasicrystals. Nature 428, 157–160 (2004).
Fischer, S. et al. Colloidal quasicrystals with 12-fold and 18-fold diffraction symmetry. Proc. Natl Acad. Sci. USA 108, 1810–1814 (2011).
Hayashida, K., Dotera, T., Takano, A. & Matsushita, Y. Polymeric quasicrystal: mesoscopic quasicrystalline tiling in ABC star polymers. Phys. Rev. Lett. 98, 195502 (2007).
Xiao, C. et al. Dodecagonal tiling in mesoporous silica. Nature 487, 349–353 (2012).
Talapin, D. V. et al. Quasicrystalline order in self-assembled binary nanoparticle superlattices. Nature 461, 964–967 (2009).
Förster, S. et al. Quasicrystalline structure formation in a classical crystalline thin-film system. Nature 502, 215–218 (2013).
Wasio, N. A. et al. Self-assembly of hydrogen-bonded two-dimensional quasicrystals. Nature 507, 86–89 (2014).
Chen, H., Li, D. X. & Kuo, K. H. New type of two-dimensional quasicrystal with twelvefold rotational symmetry. Phys. Rev. Lett. 60, 1645–1648 (1988).
Conrad, M., Krumeich, F. & Harbrecht, B. A dodecagonal quasicrystalline chalcogenide. Angew. Chem. Int. Ed. 37, 1383–1386 (1998).
Lifshitz, R. & Diamant, H. Soft quasicrystals—why are they stable? Phil. Mag. 87, 3021–3030 (2007).
Dotera, T. Toward the discovery of new soft quasicrystals: from a numerical study viewpoint. J. Polym. Sci. B 50, 155–167 (2011).
Ungar, G. & Zeng, X. Frank–Kasper, quasicrystalline and related phases in liquid crystals. Soft Matter 1, 95–106 (2005).
Keys, A. S. & Glotzer, S. C. How do quasicrystals grow? Phys. Rev. Lett. 99, 235503 (2007).
Yang, Z., Wei, J., Bonville, P. & Pileni, M.-P. Beyond entropy: magnetic forces induce formation of quasicrystalline structure in binary nanocrystal superlattices. J. Am. Chem. Soc. 137, 4487–4493 (2015).
Lee, S., Bluemle, M. J. & Bates, F. S. Discovery of a Frank–Kasper σ phase in sphere-forming block copolymer melts. Science 330, 349–353 (2010).
Iacovella, C. R., Keys, A. S. & Glotzer, S. C. Self-assembly of soft-matter quasicrystals and their approximants. Proc. Natl Acad. Sci. USA 108, 20935–20940 (2011).
Goldman, A. I. & Kelton, R. F. Quasicrystals and crystalline approximants. Rev. Mod. Phys. 65, 213–230 (1993).
Gähler, F. Quasicrystal Structures from the Crystallographic Viewpoint (ETH Zürich, 1988).
Gähler, F. in Quasicrystalline Materials (eds Janot, D. & Dubois, J. M.) 272–284 (World Scientific, 1988).
Niizeki, N. & Mitani, H. Two-dimensional dodecagonal quasilattices. J. Phys. A 20, L405–L410 (1987).
Baake, M., Klitzing, R. & Schlottmann, M. Fractally shaped acceptance domains of quasiperiodic square–triangle tilings with dodecagonal symmetry. Phys. A 191, 554–558 (1992).
Kawamura, H. Statistics of two-dimensional amorphous lattice. Prog. Theor. Phys. 70, 352–365 (1983).
Leung, P. W., Henley, C. L. & Chester, G. V. Dodecagonal order in a two-dimensional Lennard–Jones system. Phys. Rev. B 39, 446–458 (1989).
Oxborrow, M. & Henley, C. L. Random square–triangle tilings. Phys. Rev. B 48, 6996–6998 (1993).
Widom, M. Bethe ansatz solution of the square–triangle random tiling model. Phys. Rev. Lett. 70, 2094–2097 (1993).
Grimm, U. & Joseph, D. in Quasicrystals (eds Suck, J.-B., Schreiber, M. & Häussler, P.) 199–218 (Springer Series in Materials Science 55, Springer, 2002).
Dzugutov, M. Formation of a dodecagonal quasicrystalline phase in a simple monatomic liquid. Phys. Rev. Lett. 70, 2924–2927 (1993).
Barkan, K., Diamant, H. & Lifshitz, R. Stability of quasicrystals composed of soft isotropic particles. Phys. Rev. B 83, 172201 (2011).
Barkan, K., Engel, M. & Lifshitz, R. Controlled self-assembly of periodic and aperiodic cluster crystals. Phys. Rev. Lett. 113, 098304 (2014).
Dotera, T., Oshiro, T. & Ziherl, P. Mosaic two-length-scale quasicrystals. Nature 506, 208–211 (2014).
Glotzer, S. C. Assembly engineering: materials design for the 21st century. Chem. Eng. Sci. 121, 3–9 (2015).
Barth, J. V. Fresh perspectives for surface coordination chemistry. Surf. Sci. 603, 1533–1541 (2009).
Lin, N., Stepanow, S., Ruben, M. & Barth, J. V. Surface-confined supramolecular coordination chemistry. Top. Curr. Chem. 287, 1–44 (2009).
Bünzli, J.-C. G. Benefiting from the unique properties of lanthanide ions. Acc. Chem. Res. 39, 53–61 (2006).
Klyatskaya, S. et al. Surface-confined self-assembly of di-carbonitrile polyphenyls. Adv. Funct. Mater. 21, 1230–1240 (2011).
Schlickum, U. et al. Metal–organic honeycomb nanomeshes with tunable cavity size. Nano Lett. 7, 3813–3817 (2007).
Écija, D. et al. Five-vertex Archimedean surface tessellation by lanthanide-directed molecular self-assembly. Proc. Natl Acad. Sci. USA 110, 6678–6681 (2013).
Urgel, J. I. et al. Five-vertex lanthanide coordination on surfaces: a route to sophisticated nanoarchitectures and tessellations. J. Phys. Chem. C 118, 12908–12915 (2014).
Urgel, J. I. et al. Surface-supported robust two-dimensional lanthanide-carboxylate coordination networks. Small 11, 6358–6364 (2015).
Barth, J. V., Brune, H., Ertl, G. & Behm, R. J. Scanning tunneling microscopy observations on the reconstructed Au(111) surface: atomic structure, long-range superstructure, rotational domains, and surface defects. Phys. Rev. B 42, 9307–9318 (1990).
Joseph, D. & Elser, V. A model of quasicrystal growth. Phys. Rev. Lett. 79, 1066–1069 (1997).
Müllegger, S. et al. Organic molecular beam deposition of oligophenyls on Au(111): a study by X-ray absorption spectroscopy. ChemPhysChem 7, 2552–2558 (2006).
Marschall, M. et al. Supramolecular organization and chiral resolution of p-terphenyl-m-dicarbonitrile on the Ag(111) surface. ChemPhysChem 11, 1446–1451 (2010).
Klappenberger, F. et al. Uniform π-system alignment in thin films of template-grown dicarbonitrile–oligophenyls. Adv. Funct. Mater. 21, 1631–1642 (2011).
Henze, S. K. M. et al. Vertical bonding distances of PTCDA on Au(111) and Ag(111): relation to the bonding type. Surf. Sci. 601, 1566–1573 (2007).
Acknowledgements
We thank M. Baake, M. Engel and M. Garnica for fruitful discussions and suggestions, as well as M. Ruben and S. Klyatskaya for providing the molecular linkers. This work was supported by a European Research Council Advanced Grant MolArt (No. 247299), the European Commission FP7-PEOPLE-2011-COFUND AMAROUT II program, the Spanish Ramón and Cajal Program (No. RYC-2012-11133), the Comunidad de Madrid (project MAD2D), the Hong Kong Research Grants Council (No. 603213) and the TUM-HKUST Sponsorship Scheme for Targeted Strategic Partnerships. W.A. acknowledges funding by the German Research Foundation (DFG) via a Heisenberg professorship.
Author information
Authors and Affiliations
Contributions
D.E., J.I.U., N.L. and J.V.B. conceived and designed the experiments. G.L., R.Z. and J.I.U. performed the experiments. D.E., J.I.U., C.-A.P. and J.V B. analysed the data. D.E., J.I.U., C.-A.P., W.A., N.L. and J.V.B. co-wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 2643 kb)
Rights and permissions
About this article
Cite this article
Urgel, J., Écija, D., Lyu, G. et al. Quasicrystallinity expressed in two-dimensional coordination networks. Nature Chem 8, 657–662 (2016). https://doi.org/10.1038/nchem.2507
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nchem.2507
This article is cited by
-
Topological dual and extended relations between networks of clathrate hydrates and Frank-Kasper phases
Nature Communications (2023)
-
A columnar liquid quasicrystal with a honeycomb structure that consists of triangular, square and trapezoidal cells
Nature Chemistry (2023)
-
Chiral self-assembly of terminal alkyne and selenium clusters organic-inorganic hybrid
Nano Research (2022)
-
On-surface preparation of coordinated lanthanide-transition-metal clusters
Nature Communications (2021)
-
Chemical engineering of quasicrystal approximants in lanthanide-based coordination solids
Nature Communications (2020)