A designable surface via the micro-molding process

Abstract

A rapid prototyping process was presented to fabricate a nylon honeycomb microstructure coated with parylene C. The surface structure was designed to obtain a hydrophobic surface using the volume of fluid (VOF) model. With the micro-molding technique, the contact angle of the polymer surface could be designed and fabricated by changing the different microstructure surface die-steel mold inserts. For the honeycomb (20 μm width and 60 μm depth) microcavity side wall, an average micro-molding filling percentage of 95% could be achieved by using a three-section constant-pressure molding process. The solid surface wettability is governed by both the geometrical microstructures and the surface energy. A 2 μm parylene C layer was deposited on the nylon honeycomb microsurface to reduce the surface energy. To design honeycomb structures with different microcavity densities, the contact angle of these artificial surfaces could change from 91° to 130°. From a comparison of the contact angle measurements with the different models, the honeycomb-structured microsurface could be described by the Cassie–Baxter model. The errors between the VOF simulation and the measured data were <10%. The drag reduction performance of the honeycomb microplates was investigated in a water tunnel with a high Reynolds number (from 0.5×10⁶ to 4.6×10⁶). As a result, the honeycomb microplates showed a maximum drag reduction rate of 36±0.6% in comparison with the bare plates in such turbulent flow. Benefiting from the replaceable mold insert, more designable microstructure polymer surfaces can be manufactured by this rapid prototyping technique.

Introduction

Wetting is a common phenomenon in daily production and life. Hydrophobicity is also an important property of solid surfaces. The artificial control of solid surface wettability and the preparation of materials exhibiting this phenomenon are becoming areas of focus for research. Wetting is the macroscopic interaction between a solid surface structure and liquid, and solid–liquid interface molecules. A common parameter used to quantify surface hydrophobicity is the contact angle^1,2. There are several contact angle models to explain the liquid–solid interface status. Wenzel³ believed that a liquid will fill any grooves on a coarse surface. Therefore, the real solid–liquid contact area is larger than the apparent geometric contact area, and the hydrophobicity is enhanced. Cassie⁴ considered that the liquid droplets on the hydrophobic surface would not fill the grooves because air remains in the bottom of the grooves. Therefore, the apparent geometric contact is a solid–liquid–gas three-phase contact. Cassie and Baxter⁵ suggested that hydrophobic, rough or even microstructured surfaces could suspend tiny liquid droplets, with air being partially trapped in the spaces between the droplets and the surface. The equations for contact angles of composite surfaces can be deduced from the perspective of thermodynamics.

Since Onda⁶ first prepared an artificial hydrophobic surface, the methodologies to synthesize and construct designable hydrophobic surfaces have attracted considerable attention. Kee Scholten and Ellis Meng⁷ presented a submicron fabrication method to create flexible hydrophobic structures. The critical dimensions of the vapor-deposited parylene-coated film include a thickness as small as 250 nm. Youngsam Yoon et al prepared hierarchical hydrophobic surfaces using four different materials: silica nanoparticles, carbon nanotubes, SU-8 and polydimethylsiloxane (PDMS). The contact angle of these surfaces could be more than 160° (Ref. 8). Chen Zhilei et al developed a facile super-hydrophobic surface fabrication process. The magnetron-sputtered aluminum film was treated by cathodic electrochemical etching and myristic acid modification. The static water contact angle on such a surface was larger than 165° (Ref. 9). Different hydrophobic microsurface architectures, such as sawtooth grooves and rectangular grooves, have been successfully developed^10–14.

Many different fabrication processes have also been developed to generate hydrophobic surfaces¹⁵. Steam-induced phase separation could introduce a surface with a contact angle of 163° on a polystyrene-dimethylsilane copolymer (PS-b-PDMS) film¹⁶. Using nano-imprinting, lotus leaf-shaped, concave micro-PDMS with a contact angle >150° could be fabricated¹⁷. Due to the maturity of the nanoparticle synthesis, ZnO¹⁸, TiO₂ (Ref. 19), Al₂O₃ (Ref. 20) and organic silicone^21,22 have been utilized in the sol-gel process to achieve surface hydrophobicity. Those nanoparticles can generate micrometer-sized holes on the surface after drying during the sol-gel process. For instance, a nanofiber structure surface with a contact angle greater than 170° could be constructed using an alumina-polyvinyl alcohol system²³.

Nevertheless, the hydrophobicity of these surfaces could not usually be designed. In addition, a large hydrophobic surface area is difficult to mass-produce. Recently, with the development of the micro-molding technique, various tailorable microsurface structures on polymer substrates could be mass-produced²⁴. State-of-art micro electron discharge machining (micro-EDM) was also developed simultaneously to fabricate microstructures on the scale of several tens of micrometers on a die-steel surface²⁵.

In this work, a process to manufacture designable hydrophobic polymer surfaces was illustrated. Using fast-exchange mold insertion, honeycomb microsurface structures with the desired contact angle could be easily fabricated and assembled.

Materials and methods

Surface contact angle theory

The contact angle is commonly used to characterize surface hydrophobicity. This angle is the intersection between the liquid–gas interface and the solid surface once a liquid comes into contact with the solid surface. If the measured contact angle is larger than 90°, the surface is called hydrophobic. If the contact angle of a surface is smaller than 90°, the surface is called hydrophilic. There are several classical wetting models: Young’s model, the Wenzel model, the Cassie model and the Cassie–Baxter model (Figure 1). Young’s model demonstrates the wettability of a smooth solid surface, and the equation for the contact angle can be written as follows:

$$\begin{array}{}\text{(1)}& \cos {\theta }_{\mathrm{e}}=\frac{\left({\gamma }_{\mathrm{sv}}-{\gamma }_{\mathrm{ls}}\right)}{{\gamma }_{\mathrm{lv}}}\end{array}$$

where γ_sv, γ_ls, γ_lv and θ_e are the surface tension of the solid–vapor interface, the surface tension of the solid–liquid interface, the surface tension of the liquid–vapor interface and the intrinsic contact angle of the ideal solid surface, respectively.

Figure 1

(a) Schematic diagram of Young’s model, (b) schematic diagram of the Wenzel model, (c) schematic diagram of the Cassie model and (d) schematic diagram of the Cassie–Baxter model.

The Wenzel model describes the spread of droplets on a roughened surface. Wenzel assumes that the microgrooves on a surface can be completely filled with liquid. This increases the liquid–solid contact area. The surface tensions between θ_w and θ_e are given by the Wenzel model:

$$\begin{array}{}\text{(2)}& \cos {\theta }_{\mathrm{w}}=r\cos {\theta }_{\mathrm{e}}\end{array}$$

where r is the ratio between the actual solid–liquid contact area and the smooth solid surface of the solid–liquid contact area.

Unlike the Wenzel model, the Cassie model assumes that the liquid droplet cannot enter the microgrooves on the roughened surface. In this model, the derivation of the composite contact angle is defined as follows:

$$\begin{array}{}\text{(3)}& \cos {\theta }_{\mathrm{C}}=f_1\cos {\theta }_1+f_2\cos {\theta }_2\end{array}$$

where ƒ₁ is the solid surface percentage, ƒ₂ is the gas surface percentage and ƒ₁+ƒ₂=1. θ₁ is the solid surface contact angle, and θ₂ is the gas surface contact angle. The default value of both contact angles is 180°. This equation indicates that the contact angle will increase as the solid fraction decreases in the Cassie state.

The abovementioned models are hypotheses under ideal conditions. Most liquid–solid interface situations can be described by these models. Therefore, Cassie and Baxter derived an empirical formula for the general conditions called the Cassie–Baxter model:

$$\begin{array}{}\text{(4)}& \cos {\mathit{\theta }}_w=\left(f_1+\frac{\mathrm{\pi }ax}{{\left(a+b\right)}^2}\right)\cos {\theta }_e+f_1-1\end{array}$$

where x is the infiltration depth of the droplets into the microgrooves, a is the diameter of the microgroove and b is the microgroove spacing.

With the rapid development of numerical simulations in the phase interface model, complex situations on a solid surface can be analyzed and predicted. By using the algorithm rRESPA reference system propagator algorithm, the spread of pure water droplets on graphitic surfaces can be studied. Using numerical integration with multiple time step sizes, the initial transition radius of the droplet ranging from 20 to 80 nm could be revealed²⁶. Based on the multicomponent and multiphase Lattice Boltzmann schemes, the accuracy of the numerical simulation could be enhanced to only 10–20% error for contact angle prediction²⁷. The impact of droplets spreading on a paper was investigated by utilizing a VOF two-phase flow finite element simulation model. Toivakka not only revealed that the droplet size, velocity, viscosity and surface tension are the main influencing factors for droplet spreading but also summarized an empirical formula for the maximum droplet spreading diameter²⁸.

Considering that the minimum size of the micro-polymer surface structures is ~20 μm in this work, the fluid conditions for such liquid–gas–solid interfaces still satisfy the Navier-Stokes equations. Hence, the VOF model²⁹ was selected to predict the dynamic behavior of a water droplet falling on an artificial honeycomb polymer microsurface structure. The numerical simulations could also guide and optimize the design of the microsurface structure using the quick-exchange mold insert according to the micro-molding process limitations.

Hydrophobic structure design and modeling

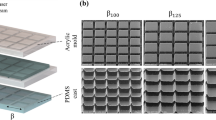
The hydrophobic micro-honeycomb architecture was sketched using SolidWorks (2014 sp5). To study the effect of the honeycomb microcavity density on the contact angle of this artificial surface, the distance to the center of the honeycomb microcavities was set as 80 μm and was held constant, whereas the widths of the side walls between adjacent groove structures were 11.2 μm, 14.4 μm, 17.6 μm, 20.8 μm and 24 μm, respectively. Thus, the surface structure duty-ratios were 0.14, 0.18, 0.22, 0.26, and 0.30, respectively. The honeycomb microstructure was designed to be fabricated on a hexagonal plastic plate, as shown in Figure 2, because the micro-molding technique can construct the macro and micro features simultaneously. The assembling joint hasps were designed on the plastic plate edges as well. These flexible hydrophobic plastic plates can be assembled onto the curved surfaces.

Figure 2

The honeycomb microstructures and the joint hasp structures were designed on a 1.5 mm thick tailorable polymer plate.

A numerical simulation tool (ANSYS (R14.5) FLUENT) was utilized to create the VOF modeling with the mesh tool GAMBIT (2.4.6).

Micro-molding process

Die-steel (S136, ASSAB, Switzerland) mold inserts were fabricated by micro-EDM (AgieCharmillesROBOFORM350γ, GFMachiningSolutions, Switzerland) with a multi-station process (discharge voltage: 20–100 V; discharge distance: 5–10 μm). The multi-station narrow-slit electrodes (copper–tungsten alloy (70% W)) were carved by a five-axis machining center (Mikron XT-one, Mikron Holding AG, Switzerland). Finally, the mold insert was completed by slow-speed wire cut electrical discharge machining (AgieCharmillesCUT200SP, GFMachiningSolutions, Switzerland).

Nylon (PA6B30S, BASF, Germany) granules were rapidly selected as prototypes of five honeycomb microstructures with different densities using a precision molding machine (SE100EV, Sumitomo, Japan). To further enhance the nylon plate hydrophobicity, 2 μm thick parylene C was deposited by Chemical Vapor Deposition (CVD) (Plasmalab System100 PECVD, Oxford Instruments, UK).

Morphology and contact-angle measurements

All the microstructural features on the mold inserts and the injected nylon plate were measured by an optical profilometer (WYKO NT1100, Veeco, USA). The contact angle of surface structures with different duty-ratios was measured by an optical contact angle measuring instrument (OCA20, Dataphysics, Germany).

Water tunnel experiment

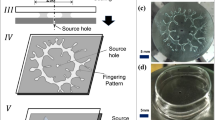
The drag reduction rate measurements were carried out in a high-speed water tunnel at the China Ship Scientific Research Center, as shown in Figure 3. During the water tunnel experiment, different nylon plates were assembled on the wing plate (50 cm long, 25 cm wide and 2 cm thick) using a polyurethane adhesive. The wing plate was vertically fastened in the middle of the water tunnel. The surface of the wing plate was parallel to the fluid flow direction. With the help of a torsion meter fastened to the bracket, the fluid friction on the wing plate could be measured. The water speed in the water tunnel was increased from 3.0 to 23.0 m s⁻¹, corresponding to an increase in Reynolds number (Re) from 0.5×10⁶ to 4.6×10⁶. Under the same assembly conditions, the drag reduction effects of the honeycomb microsurface plates and the bare plates were investigated.

Figure 3

Picture of (a) the water tunnel and (b) the assembled hydrophobic wing plate.

Results

The micro-EDM protocols were examined to achieve suitable etching morphology and roughness. Because the die-steel surface was polished prior to the micro-EDM process, the surface roughness of the die-steel mold insert was ~90±0.2 nm. The sidewall inclination angles of the micropillars (64±0.5 μm height, Figure 4a) on the mold insert surface were ~84±0.4°. Such mold insert morphology could satisfy not only the molding demand for surface roughness but also the molding draft angle requirement. Due to its toughness, low friction coefficient and low cost, nylon has been widely applied as an injection material (properties shown in Table 1). Using multilevel injection and a three-section pressure-holding process, a micro-molding filling percentage of 95% could be achieved for a microcavity side wall with a depth-to-width ratio of 3:1 (60±0.4 μm depth, Figure 4b). The optimized injection molding process parameters are listed in Table 2. The injection-molded microstructures had a good surface roughness (90±2 nm) and a sharp sidewall (84±0.4° tilt angles), as shown in Figure 5. Ultimately, a 2 μm thick parylene C layer was deposited on the surfaces. The parylene CVD process could provide a seamless coating, good inertness, dehumidification and a small friction coefficient.

Figure 4

(a) Contours of the die-steel mold insert surface and (b) contours of the nylon plate surface.

Table 1 Physical properties of nylon PA6B30S.

Table 2 Optimized parameters for the micro-molding injection processes.

Figure 5

SEM photo of a honeycomb nylon microsurface structure.

The contact angles of the different surface plates were measured, as shown in Figure 6. The parylene C–coated plates showed an average contact angle enhancement of 30±3° compared with the nylon plates. As the surface structure duty-ratio decreased, the hydrophobicity gradually increased. Compared with the bare plates, the plates with a duty-ratio of 0.14 had a maximum contact angle difference of ~32±1°.

Figure 6

Contact angle of nylon and parylene-coated surfaces with different duty-ratio structures. A duty-ratio of 1.0 indicates a smooth surface. The testing droplet volumes were 3 μl. The average contact angles of the nylon plates were 98.4±1.1°, 99.6±1.0°, 96.3±1.6°, 95.1±1.6°, 93.5±1.3° and 67.8±1.7°, whereas the average contact angles of the parylene-coated plates were 130.4±0.8°, 127.8±0.7°, 123.5±1.7°, 121.2±1.2°, 119.4±1.4° and 95.6±0.8°, corresponding to structure duty ratios of 0.14, 0.18, 0.22, 0.26, 0.30 and 1.0, respectively.

Discussion

To predict the contact angle of honeycomb microstructure designs with different duty-ratios, a transient VOF model was established (Figure 7 and the Supplementary Material). This model was applied to simulate the dynamic spreading process after impact of a water droplet on the artificial microstructure surface. The simulated physical phenomena were simplified as follows: a static water droplet (3 μl) falls freely and collides vertically with the solid surface below (0.08 mm away). All the material boundary conditions were set based on the parylene C properties. After the model was established, a quadrilateral mesh was utilized to accelerate the computational convergence. With the help of the pressure implicit splitting of operators algorithm, the different time steps were verified to increase the convergence speed. Finally, a time step of 10⁻⁶ s was selected to obtain an accurate droplet falling dynamic process. All the selected simulation parameters are listed in Table 3.

Figure 7

The droplet morphology at different times. (a) The initial state of the droplet, (b–d) the morphological changes of the droplet during impact and (e) the final steady state of the droplet. The red area represents the droplet, and the blue area represents the air.

Table 3 The volume of fluid model analog parameter set.

Neglecting liquid evaporation and gravity, the droplet was presented as a 0.68 mm radius sphere, as shown in Figure 7a. Once the droplet impacted the artificial hydrophobic surface, a springback movement would be triggered, as shown in Figure 7b–7d. Similar phenomena were observed during the contact angle measurements. When the calculation reaches convergence, it means that the droplet on the surface reaches a steady state. The contact angle can then be obtained by plotting the tangent lines along the contours of the liquid–solid–gas three-phase contact interface, as shown in Figure 7e. For a surface with a duty-ratio of 0.14, the simulated contact angle could reach 136.5°. Under the simulated steady state, ~5.5% of the volume of the honeycomb microcavities would be filled by the droplet, which indicated that this artificial surface could be more precisely described by the Cassie–Baxter model.

Basically, structures with lower duty-ratios could trap more air inside the microcavities. Because the volume of the liquid droplet was limited, the contours of the liquid–solid–gas three-phase contact interfaces would be flatter. A surface with a low duty-ratio would be much closer to the Cassie model. The accuracy of the numerical simulation was verified by comparison of the measured data with the Wenzel model, the Cassie model and the Cassie–Baxter model (Figure 8). As a result, the VOF-simulated data had only ~10% higher error than the measured data, which might be due to gravity force effects. The r values in the Wenzel model and the ƒ₁ values in the Cassie model could be obtained from the image analysis of the contact angle measurements. Through the simulation, a Cassie–Baxter model could be established to closely approximate the honeycomb microsurface contact angle data. Unlike other models, the established VOF model could predict more microscopic dynamic details of the liquid–solid–gas interfaces on the complex surface microstructures.

Figure 8

For the honeycomb-structured microsurfaces with different duty-ratios, the contact angles calculated using different models were compared with the measured data. The values of r in the Wenzel model are 2.55, 2.40, 2.25, 2.10 and 1.95; the values of ƒ₁ in the Cassie model are 0.28, 0.36, 0.44, 0.51 and 0.54; the values of x in the Cassie–Baxter model are 2.8 μm, 3.1 μm, 3.2 μm, 3.4 μm and 3.7 μm; and the calculated values correspond to duty-ratios of 0.14, 0.18, 0.22, 0.26, 0.30, respectively.

In principle, the smaller solid–liquid contact surface area could cause the liquid droplet to roll off the surface more easily. To reveal the drag reduction effect of the honeycomb microstructure on the large surface area, more than 100 honeycomb microplates were assembled on a wing plate for the water tunnel experiments. As a control, bare plates were also assembled on the wing plate. According to the measured friction on the wing plate, the fluidic friction for the assembled wing plates on the two different microplates increased monotonically with increasing Reynolds number. Under the same assembly conditions, the honeycomb microplates could reduce the drag force by ~36±0.6% compared with the bare plates when Re reached 4.5×10⁶ (Figure 9). When Re increased to 3.0×10⁶, the drag reduction rate did not increase dramatically. This might be caused by the turbulent flow breaking the interfaces between the liquid and the trapped air within the honeycomb microcavities. With smaller honeycomb cavities and a smoother assembly, a better drag reduction performance can be expected.

Figure 9

Drag reduction test of the assembled honeycomb microplate and the assembled bare plate. The average measurement errors were approximately 1–2%.

Conclusion

In this paper, a honeycomb-structured microsurface was designed and modeled. Using a quick-exchange mold insert, the different microstructure surfaces could be mass-produced. The micro-molding injection process could provide a filling rate of 95% for the 68 μm wide and 60 μm deep honeycomb microcavities. The honeycomb microstructure could achieve a contact angle of ~30±0.6° to increase the surface hydrophobicity. The 2 μm parylene C deposition layer could further result in a contact angle of ~30±2°. For the honeycomb microsurface with a duty-ratio of 0.14, the contact angle was as high as 130±0.5°. Meanwhile, the established VOF model could provide a precise prediction (only 10% error) for the artificial surface contact angle. Furthermore, the assembled honeycomb microplates showed a significant drag reduction rate (36±0.6%, Re=4.5×10⁶) compared with the bare plates. In summary, a designable and tailorable honeycomb-structured microsurface could be mass-produced and assembled into a surface with a large drag reduction for vessels.