Abstract
The continuing trend of exponential growth in data communications and processing are driving the need for large-scale heterogeneous integration. Similar to the trend we have observed in electronic integrated circuit development, we are witnessing a growing trend in 3D photonic integrated circuits (PICs) development in addition to that in 2D PICs. There are two main methods for fabricating 3D PICs. The first method, which utilizes ultrafast laser inscription (ULI), offers freeform shaping of waveguides in arbitrary contours and formations. The second method, which utilizes multilayer stacking and coupling of planar PICs, exploits relatively mature 2D PIC fabrication processes applied to each layer sequentially. Both the fabrication methods for 3D PICs have advantages and disadvantages such that certain applications may favor one method over the other. However, a joining of 2D PICs with 3D PICs can help develop integrated microsystems with new functionalities such as non-mechanical beam steering, space-division multiplexing (SDM), programmable arbitrary beam shaping, and photonic signal processing. We discuss examples of 3D PICs and 2D/3D integrated PICs in two applications: SDM via orbital-angular-momentum (OAM) multiplexing/demultiplexing and optical beam steering using optical phased arrays. Although a 2D PIC by itself can function as an OAM multiplexer or demultiplexer, it has limitations in supporting both polarizations. Alternatively, a 3D PIC fabricated by ULI can easily support both polarizations with low propagation loss. A combination of a 3D PIC and a 2D PIC designed and fabricated for OAM applications has successfully multiplexed and demultiplexed 15 OAM states to demonstrate polarization-diversified SDM coherent optical communications using multiple OAM states. Coherent excitation of multi-ring OAM states can allow highly scalable SDM utilizing Laguerre–Gaussian modes or linearly polarized (LP) modes. The preliminary fabrication of multi-ring OAM multiplexers and demultiplexers using the multilayer 3D PIC method and the ULI 3D PIC method has also been pursued. Large-scale (for example, 16×16 optical phased array) 3D PICs fabricated with the ULI technique have been demonstrated. Through these examples, we show that heterogeneous 2D/3D photonic integration retains the advantages of 2D PICs and 3D waveguides, which can potentially benefit many other applications.
Similar content being viewed by others
Introduction: Why photonics? Why heterogeneous integration? Why 3D?
The amount of information we process has been continuing its remarkable trend of exponential growth. Sustainably supporting such explosive growth requires scalable, high-yield, and cost-effective integration of microsystems. For two-dimensional electronic integrated circuits (2D EICs), Moore’s law stated more than five decades ago1 that the number of transistors that could be placed inexpensively on an electronic integrated circuit (EIC) doubled approximately every 2 years. As a corollary, Dennard’s law2 claimed that the power efficiency will also scale at the same pace with Moore’s law. Although the remarkable exponential scalability in integration still continues after five decades, Dennard’s law, which kept pace with Moore’s law for four decades, started to fail in 2004. The International Technology Roadmap for Semiconductors (ITRS)3 mentions a ‘red brick wall’ because there is no known technology solution below the 7-nm technology where complementary metal-oxide-semiconductor (CMOS) scaling is expected to stop (as already noted, CMOS power density scaling stopped in 2004). The two main causes for these limitations are the increases in leakage currents at such small scales (because the atoms do not scale with CMOS) and the limitations of electronics in interconnects (because of the skin effects and impedances of electronic interconnects). The arrival of chip multicore processors in 2006 is providing a temporary reprieve for these limitations by offering parallel processing capabilities in multicores without increasing the clock speed. An interesting new trend is the exponential increases in the number of cores in modern processors. In such parallel processing where interconnects are the bottlenecks, photonics provides parallelism and high capacity independently of distance. Hence, the hybrid integration of photonics and electronics can bring the best of both worlds where bosons (photons) and fermions (electrons) exhibit two sets of complementary traits. Photonic integrated circuits (PICs) take advantage of large bandwidth, low latency and low transmission loss, and electrical circuits exploit complicated signal processing. Table 1 lists commonly used photonic integration platforms and their attributes. Because the size of the electronics industry market is greater than four times that of the photonics counterpart, photonic integration platforms have always leveraged electronic integration counterparts such as CMOS for silicon and heterojunction bipolar transistor (HBTs) and high-electron mobility transistors for III–V platforms. Hence, it was not coincidental that the concept of co-integration of photonics and electronics emerged in the form of optoelectronic integrated circuits (OEICs)4,5 for III–V and CMOS-photonics for silicon6.
More importantly, both EICs and PICs have recently been seeking heterogeneous integration. Modern EICs often integrate heterogeneous circuits involving analog and digital or involving silicon CMOS and Ge bipolar transistor circuits. Likewise, photonic integration also benefits from integrating heterogeneous materials. Although silicon photonics is rapidly emerging as a viable and possibly ubiquitous photonic integration platform, silicon lacks optical gain, Pockels effect, and Faraday effect, which are useful for realizing lasers, phase modulators, and non-reciprocal devices. Hence, co-integration of silicon with III–V materials, electro-optical dielectrics, and magneto-optical materials can greatly enhance the functionalities of heterogeneously integrated microsystems.
As a substrate for an integration platform, the silicon substrate proves to be the most economical and scalable. The CMOS EIC industry is moving towards a 450-mm diameter silicon wafer platform with the ⩽14 nm gate CMOS technology, and 7 nm CMOS technology has recently been demonstrated. As a photonic device integration platform, silicon photonics is also gaining strong grounds. It is well known that the main reason behind the successful and practical development of multibillion-transistor circuits based on silicon CMOS is the availability of high-quality and dense passivation available from silicon’s natural oxide, SiO2. Interestingly, silicon photonics also benefits from the same high-quality silicon dioxide available for realizing high-contrast and low-loss Si/SiO2 waveguides exploiting a low-loss interface between silicon and SiO2. Owing to the availability of high-quality, large-scale, and low-cost silicon wafers together with a large number of CMOS foundries, silicon has recently emerged as a preferred integration platform.
Integration efforts in both EICs and PICs have thus far been active primarily in 2D. Because the number of transistors exceeded 10 billion per die, high-density integration has extended to 3D integration by stacking multiple layers of 2D EICs using through-silicon vias (TSVs)7. Three-dimensional EICs offered a number of performance enhancements over 2D EICs, primarily because of shorter electrical wiring requirements. They generally offer8 (a) lower power consumption due to a reduced number of repeaters and equalizers over shorter communication distances, (b) lower noise and jitter on shorter interconnects, and (c) higher packing density in 3D. In photonics, too, rapid advances in 2D photonic integrated circuits (PICs) have also motivated us to coin a term ‘photonic Moore’s Law’9,10. More recently, 3D photonic integration has emerged as very important steps towards bringing new functionality and a higher degrees of integration to microsystems11–20. For instance, space division multiplexing (SDM) based on 3D photonic integration overcomes limitations imposed on 2D photonics in handling the spatial degree of freedom and polarization dependence resulting from the fact that all waveguides must lie within the same 2D plane. Heterogeneous 2D and 3D photonic integration will bring diverse and complementary functions in a dense footprint. This paper overviews heterogeneous 2D and 3D photonic integration technologies and predicts their future directions.
Monolithic versus hybrid heterogeneous integration in 2D
Heterogeneous integration can be achieved by either monolithic integration or hybrid integration. In particular, monolithic integration by hetero-epitaxy is attractive in that it can exploit large host substrates (for example, silicon wafers) and epitaxially grow III–V or other compound materials at a wafer scale at dimensions defined by the host substrate. For instance, InP lasers can be realized across 450-mm silicon wafers even when high-quality InP wafers are limited to ~75 mm diameters. However, the main challenge has been to overcome the lattice mismatch and to hetero-epitaxially grow low-defect materials. Epitaxial lateral overgrowth (ELO) technology has localized such defects within narrow apertures and grown reasonably high-quality crystals above dielectrics laterally seeded from the host materials through the apertures. Moreover, more recent work has exploited the 3D confinement of quantum dots to prevent the carriers from migrating to dislocations and demonstrated record performance on any lasers realized on silicon. In another recent work, the rapid-melt-growth (RMG) method has demonstrated high-quality germanium crystal growth from deposition of an amorphous germanium layer followed by rapid thermal annealing (melting), which is seeded by underlying silicon atoms reachable through nano-apertures formed similarly to those used for ELO. However, the RMG method is not as effective for III–V compound semiconductors on silicon because of twin formations in III–V materials. Overall, monolithic integration by heteroepitaxy remains challenging for achieving low-defect heterogeneous integration.
In contrast to monolithic integration, hybrid integration methods do not attempt material growth but utilize various bonding mechanisms between dissimilar (or similar) materials already grown on individual substrates. The bonding techniques21 known to microelectronics include (1) bonding without an interlayer, which includes (1a) anodic, (1b) direct, and (1c) low-temperature van der Waals bonding; (2) bonding with a metallic interlayer, which includes (2a) eutectic, (2b) thermos-compressive, and (2c) solder bonding; and (3) bonding with an insulating interlayer, which includes (3a) glass frit and (3b) adhesive bonding. For optoelectronics, the most popular bonding methods have been (1b) direct bonding (hydrophobic or hydrophilic) and (3b) adhesive bonding. Both direct bonding and adhesive bonding offer versatile heterogeneous integration between dissimilar materials, and the difference in thermal expansion coefficients and wafer sizes typically limit the choices of materials for wafer-scale integration. Direct bonding22 includes hydrophilic and hydrophobic bonding depending on the surface treatments prior to the bonding. In hydrophilic bonding, the hydroxyl of the atom yields water vapor after the bonding. Assuming silicon wafer to silicon wafer bonding, this process initially involves the following:
The water vapor then binds with silicon to emit hydrogen gas: Si+2H2O=SiO2+2H2. In hydrophobic bonding, hydrogenated or fluorinated surfaces without oxides will bond to emit hydrogen gas: Si–H+Si–H=Si–Si +H2. Hence, in both cases, hydrogen gas can be trapped at the interfaces to cause defects, but this can be avoided by introducing vertical out-gas channels with silicon oxide to absorb the hydrogen molecules. Hydrophobic bonding requires higher bonding temperatures (>550 °C) but achieves stronger surface bonding energy (>2 J m−2) and intimate electrical bonding compared with hydrophilic bonding with a ~350 °C bonding temperature with an oxide layer at the bonding interface. Adhesive bonding using BenzoCycloButene (BCB)23, SU-8, or other interface layers has become very popular because of relatively relaxed requirements on the flatness of the bonding surfaces. Hydrophobic direct bonding has produced InP/InGaAsP edge-emitting lasers on GaAs substrates22, AlGaAs/GaAs edge-emitting-lasers on Si substrates24, and vertical cavity lasers with InP/InGaAsP active regions on GaAs/AlAs distributed Bragg reflectors25 with electrical currents flowing across the bonding interfaces. Hydrophilic direct bonding has produced AlInGaAs/InP-on-SOI hybrid lasers, modulators, and detectors achieving high-quality results with no obvious signs of additional defect-induced degradations, whereas the current flows are limited to the III–V regions without the ability to cross the bonding interface26.
3D Integration technologies
3D EICs include multiple layers of 2D EICs stacked and interconnected using TSVs7. Similarly, one type of 3D PICs have utilized orderly stacking of multilayer 2D photonic crystals to realize 3D photonic crystals27. Another type of 3D PIC utilized repeating of the combined processes of waveguide core layer deposition, lithography, etching, waveguide cladding layer deposition, and planarization (for example, chemical and mechanical polishing) to complete multilayer 3D PICs28,29 where interlayer coupling can be achieved by low-loss inverse taper waveguides30. Such 3D PICs can also be realized by wafer bonding of 2D PICs of similar31 or dissimilar32 materials while employing vertical couplers utilizing inverse taper waveguides for interlayer optical coupling. The interlayer optical coupling can also exploit photonic vias analogous to electrical TSVs, and a recent work33 has realized fabrication of photonic, electronic, and fluidic through-silicon vias in the same chip.
Perhaps, the most distinctive 3D PICs with no electronic counterpart are realized by 3D waveguide formation by ultrafast laser inscription (ULI). Direct laser writing of waveguides in dielectric material is an extremely powerful fabrication technique34. It utilizes the multi-photon nonlinear absorption of sub-bandgap photons to create permanent structural changes in a material with dimensions comparable to the writing laser’s wavelength (for example, ~1 μm3). The types of structural changes include refractive index and an increased susceptibility to chemical etching35. The induced modifications from a femtosecond train of optical pulses are strongly localized in three dimensions to the high-intensity region at the focus of a lens driven by a nonlinear absorption mechanism. This unique characteristic is what provides direct laser writing with its unique advantage over other waveguide fabrication techniques; the capability to freely form truly three-dimensional structures36. ULI has been widely demonstrated in many types of materials including amorphous glasses and crystals with measured propagation losses ⩽0.3 dB cm−1 (Refs. 37,38) in fused silica, similar to the 0.1 dB cm−1 propagation loss in 2D PICs (for example, Ge-doped silica on silicon)37,38. Furthermore, a recent demonstrations showed that high-quality three-dimensional waveguides are readily created with laser writing speeds on the order of 30 mm s−1 (Ref. 39). Finally, optical mode sizes can be adapted for a particular application by adjusting the geometry and composition of the inscribed waveguide by beam shaping of the inscribing laser or multiple scan techniques40,41. Figure 1 illustrates the ULI process that creates 3D waveguides within a bulk material where the waveguide core is formed by an increase in the local material index at the focus of the inscribing laser. For visible and near-infrared applications, fused silica and other glass materials are widely used for 3D waveguide inscription. Figure 2 shows an example of a 3D waveguide fan-out device that is fabricated by ULI. As detailed in the next section, the fan-out device can be butt-coupled to a 2D PIC (that is, planar lightwave circuit) for orbital angular momentum (OAM) applications11,12,42–44. In addition to silica, a variety of crystalline and non-crystalline materials can be used for 3D ULI waveguide applications. For instance, zinc selenide (ZnSe) is potentially a good 3D material because it is transparent from 0.5–20 μm and, although not as mature, low-loss waveguides in ZnSe45–47 and a solid-state Cr:ZnSe waveguide laser48 based on direct 3D laser writing have been demonstrated.
Schematic illustration of 3D photonic inscription where the waveguide is formed by increasing the local index of the material. The table shows how optical pulse energy, pulse repetition rate, and waveguide scan speed are adjusted to optimize the quality of the inscribed waveguide when the pulse width is held constant. Depending on the combination of laser repetition rate and mechanical scan rate, the material modification regions formed by each pulse will overlap by varying amounts. 3D, three dimensional.
Microscopic images of a ULI-fabricated 3D waveguide fan-out device for orbital angular momentum applications11,12,42–44. (a) Facet image of the output showing the circular pattern of 16 waveguides. (b) View of a from above the top edge. (c) View of the interior where waveguides fan-out to a linear array. (d) View of waveguides near the output through the top surface. ULI, ultrafast laser inscription.
Similar laser inscribing methods applied to SU-8 or other ultraviolet-sensitive polymers can lead to the creation of ‘photonic wires’ through two-photon induced polymerization of negative-tone resist in the focus of a pulsed laser beam with a large numerical aperture49. Such polymerization using laser inscription creates 3D structures with relatively tight bending radii thanks to the high contrast between the polymer (core) and the air (cladding). Photonic wire bonding between various chips has been demonstrated using this technique49.
Examples of 2D/3D integrated systems
2D/3D integrated OAM multiplexers
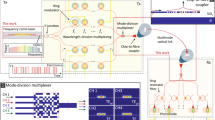
Here we visit applications of heterogeneous integrated 2D and 3D systems. For instance, SDM based on 3D photonic integration overcomes limitations imposed on 2D photonics in handling the spatial degree of freedom and polarization dependence resulting from the fact that all waveguides must lie within the same 2D plane. Heterogeneous 2D and 3D photonic integration will bring diverse and complementary functions in a dense footprint. Figure 3a shows the integratable orbital angular momentum multiplexing device’s operating principle, which relies on converting linearly varying spatial phase to azimuthal variations (that is, exp(ibℓx)→exp(iℓφ), where b is the linear (x) to azimuthal (φ) scaling factor)11,50. To illustrate, Figure 3a shows a waveguide circuit in which each single mode input (that is, ℓ=−2, −1, 0, +1, +2) will create a wavefront in the free-propagation region (FPR) with a different linear tilt. The phase-matched waveguides after the FPR sample the tilted phase front and maintain the phase tilt to the output apertures. Because the apertures are arranged in a circular pattern, they create a beam (coming out of the page) with azimuthally varying phase having topological charge ℓ. If multiple inputs are illuminated, then those inputs are multiplexed onto collinear OAM beams with ℓ-numbers determined by the input position. By reciprocity, if an outside OAM beam illuminates the apertures, then the sampled light will be focused in the FPR to a waveguide corresponding to the beam’s ℓ-number (that is, an OAM demultiplexer). Working as a demux (that is, OAM state decoder), Figure 3b shows how a circular array of waveguide grating couplers are used to sample areas (dashed circles) of an incoming beam encoded with an OAM state (that is, ℓ=1) into a corresponding array of single-mode waveguides. Careful waveguide layout ensures that they have identical optical path lengths. Thus, at the input of the free-propagation region (FPR), the azimuthally varying phase of the OAM state is converted into a linear phase front with a tilt angle determined by the incoming beam’s topological charge, as indicated in Figure 3a. The circular placement of the array waveguides at the input of the FPR focuses the light, and the tilt of the linear phase front directs it to a corresponding output. The same PIC can function as a mux instead of demux when the light propagates in the opposite direction42.
We take advantage of the 3D capability to create the geometric transformation needed to convert linear phase tilt to azimuthal phase variation. Figure 4a shows how this concept is implemented using a silica PLC (to convert input position to a linear phase tilt) whose output is coupled to a 3D PIC for geometric transformation. Figure 4b presents a close view of the 3D PIC output face showing the circular arrangement. Figure 4c shows a photo of the fabricated PLC. The waveguides on the silica PLC have an index contrast Δn of 2%. Electrical heaters on each output waveguide provide thermo-optic phase-error correction (PEC). This is used to phase match the waveguides between the FPR and the output face of the 3D PIC. Both the PLC and the input of the 3D PIC use a 127-μm waveguide pitch. The hybrid device (that is, PLC and 3D PIC) is ~30-mm long, and the waveguides on the output face form a 204-μm diameter circle with a center-to-center spacing of 40 μm (Figure 4d)11.
(a) Illustration of the silica PLC coupled to the 3D PIC. (b) 3D waveguide output facet detail. Estimated optical propagation loss is 0.2 dB cm−1. (c) Photo of fabricated silica PLC. (d) Photo of unpolished 3D PIC output face11. PIC, photonic integrated circuits.
Figure 5 summarizes the optical characteristics of the combined 2D PIC: 3D PIC device of Figure 4a, including the waveguide losses (Figure 5a), whereas the optical path lengths are matched for all individual optical paths for the 16 apertures, phase error correction (PEC)11 is important for achieving very accurate relative optical phases between the apertures for realizing high-fidelity OAM multiplexer/demultiplexers (Figures 5b–d). Figures 5g–i shows examples of the measured intensity and phase of the OAM modes (for example, ℓ=+1, –1, +6), and Figure 5e summarizes the unwrapped phase plot versus waveguide output number for all OAM states. The result shows clearly that for each OAM state, the phase is the product of 2π and the OAM charge number ℓ. Figure 5f illustrates the crosstalk between the OAM states, which indicate less than −8 dB crosstalk. A higher number of waveguide apertures and more uniform power distribution after the FPR can reduce this crosstalk further.
(a) Measured excess loss for the silica PLC and 3D waveguides. (b) Measured intensity and phase of the device’s output waveguides without PEC, (c) with PEC. (d) Measured average azimuthal phase at each output waveguide. (e) Unwrapped azimuthal phase for each OAM mode. (f) Calculated OAM mode purity. (g–i) The measured intensity and phase for three OAM modes (ℓ=+1, –1, +6)11. OAM, orbital-angular momentum; PEC, phase-error correction.
3D multi-ring waveguides for OAM applications
Multi-ring 3D waveguide design and fabrication for the OAM application are important first step towards scalable SDM. Our group has developed a 3D waveguide design tool utilizing the routing algorithm that maintains the same photonic path lengths, the minimum radius of curvature, and the minimum inter-waveguide distance. Figure 6a shows the computer-aided-design, and Figure 6b is a photograph of the fabricated multi-ring 3D waveguides at the facet. In such cases, the multi-ring OAM PICs can possibly realize the generation of arbitrary spatial waveforms such as Laguerre–Gaussian modes by adding the radial control of the optical field to the azimuthal control achieved in individual OAM PICs of each ring.
(a) Dual-ring 3D waveguide design utilizing the routing algorithm that maintains the same photonic path lengths, the minimum radius of curvature, and the minimum inter-waveguide distance, (b) a photograph of the fabricated multi-ring 3D waveguides (Corning Eagle 2000) observed at the facet. 3D, three dimensional.
3D waveguides for optical phased arrays
In addition to the spatial waveform shaping using multi-ring 3D PICs fabricated by ULI methods, the same ULI can form 3D PICs of arbitrary array shapes, including a rectangular array. Figure 7 shows the details of a 3D PIC that transforms a linear 1×256 input waveguide array into a 16×16 rectangular array of output waveguides using the ULI technique. Figure 7a shows a computer-aided design with details of the output array, Figure 7b presents a photograph of the output facet and Figure 7c presents a photograph of a portion of the input facet. As is the case with most dielectric waveguides, the index difference between the waveguide core and cladding determines the minimum bending radius due to radiation losses from the bent waveguide. Because the index difference for these ULI waveguides is ~0.5%, we chose a minimum bending radius of 20 mm, which showed negligible bending loss. Similar to the multi-ring 3D PICs, the rectangular PICs also utilized the 3D computer-aided design for precise optical path length matching of all 256 waveguides. Such 3D PICs are useful for non-mechanical beam steering51 and SDM MIMO optical communications and beamforming (for example, Hermite–Gaussian modes). Figure 8a shows an example of optical beam steering realized by heterogeneous integration of such a 3D waveguide array and a 2D PIC consisting of optical splitter waveguides and waveguide array phase shifters. Figures 8b–i illustrates optical beam steering results experimentally obtained from phase tuning the array waveguides in the 2D PIC by π, 0.75π, 0.5π, 0.25π, 0, −0.25π, −0.5π, and −0.75π between the waveguides51. Here PEC11 is conducted by phase tuning the array waveguides.
(a) 16×16 3D waveguide design utilizing a routing algorithm that maintains the same photonic path lengths, the minimum radius of curvature, and the minimum inter-waveguide distance, (b) a photograph of the fabricated 16×16 3D waveguides observed at the output facet. (c) Magnified micrograph of a portion of the 256 input waveguides. 3D, three dimensional.
(a) Optical phase array beam steering module realized by heterogeneous integration of a 3D waveguide array similar to Figure 7b and a 2D PIC consisting of optical splitter waveguides and waveguide array phase shifters. (b–i) optical beam steering results obtained from phase tuning the array waveguides in the 2D PIC by π, 0.75π, 0.5π, 0.25π, 0, −0.25π, −0.5π, and −0.75π between the waveguides51. The optical waveguide propagation loss value of the 3D waveguide was ~0.2 dB cm−1. PIC, photonic integrated circuits; 2D, two dimensional; 3D, three dimensional
Single-layer and multilayer 2D PICs for 2D/3D integration
The OAM structures can also be fabricated by using a standard single-layer 2D PIC fabrication technique (for example, silicon photonic OAM mux/demux42), and multi-ring OAM structures can be realized by stacking and integrating multilayers of the single-ring OAM devices. Figure 9a shows42 the single-layer 2D silicon photonic integrated circuit layout, which is designed for a silicon-on-insulator (SOI) material platform, optimized for TE polarization, and uses a 1-μm-wide silicon rib waveguide (effective index of 3.27). The circular grating converts the vertically incident optical beam (azimuthal polarization) into a horizontally propagating beam. Depending on the OAM state of the input beam, the 16 guided modes will have a specific linear phase variation. Because the FPR is designed based on the Rowland circle principle, it focuses the 16 beams onto five waveguide outputs according to the linearly varying phase associated with the five different OAM states (labeled as ℓ=+2, +1, 0, −1, −2). We have extended a similar fabrication technique to the silicon nitride/silicon oxide waveguide system and utilized multilayer stacking of OAM device layers to realize multi-ring OAM PICs. Figure 10 shows stacking of multiple 2D layers for arbitrary waveform shaping, Figure 10a shows a stacked device consisting of Layers 1–5, and Figure 10b presents a fabricated three-layer silicon nitride/silicon dioxide OAM device. The images of the three-layer silicon nitride/silicon dioxide OAM device are also shown here when the (Figure 10c) bottom (Layer 1), (Figure 10d) middle (Layer 2), and (Figure 10e) top (Layer 3) are illuminated. When multiple layers are coherently excited, this device can create a mode profile that can excite eigenmodes of the multimode fibers. The main disadvantage of this stacked 2D waveguide approach compared with the laser-inscribed 3D waveguide approach is the poor support of polarization diversity50. The near-surface-normal emission using the gratings makes it difficult to support radial polarization, while reasonable throughput is achieved for azimuthal polarization.
(a) Waveguide layout of silicon OAM device for multiplexing five OAM modes (ℓ=+2, +1, 0, −1, −2). (b) Fabricated silicon OAM device. The optical loss value was approximately 0.4 dB cm−1. The inset shows an SEM photo of the grating42. OAM, orbital-angular momentum; SEM, scanning electron microscope.
Stacking of multiple 2D layers for arbitrary waveform shaping. (a) Stacked device consisting of Layers 1–5. (b) Fabricated three-layer silicon nitride/silicon dioxide OAM device. Image of the three-layer silicon nitride/silicon dioxide OAM device when the (c) bottom (Layer 1), (d) middle (Layer 2), and (e) top (Layer 3) are illuminated. The optical waveguide propagation loss value was approximately 0.3 dB cm−1. OAM, orbital-angular momentum; 2D, two dimensional.
In such multilayer 3D PICs, it is important to split or combine optical waves from one waveguide layer to another. Cross-layer couplers with extremely low losses at ~0.01 dB per coupler and low crosstalk of less than −42 dB per coupler have been designed and fabricated52 in silicon nitride/silicon dioxide waveguide PICs. Figure 11a shows a schematic of a three-layer silicon nitride/silicon dioxide PIC with a 1×2 waveguide splitter53 and Figure 11b presents a fabricated two-layer silicon nitride/silicon dioxide PIC52 designed to drive the multi-ring 3D PIC shown in Figure 6b.
The two types of 3D photonic integrated circuit fabrication technologies discussed here—(a) Multilayer 3D waveguides and (b) ultrafast laser inscription 3D waveguides—have their pros and cons. Table 2 summarizes their comparisons.
Outlook and discussion
The continuing trend of exponential growth in data communications and processing will accelerate the pace of heterogeneous integration. In particular, we expect strong growth in the pace of 3D PIC development in addition to that of 2D PICs. Between the two main methods of realizing 3D PICs, the first method utilizing ULI is expected to see strong demand because of its capability to realize freely shaped waveguides of arbitrary contours and formations. Owing to the serial and sequential nature of its writing process, we expect expanded efforts to develop faster inscription recipes or to split laser beams for parallel and simultaneous writing of multiple PICs. On the other hand, the second 3D PIC fabrication method utilizing multilayer planar waveguides will also see strong demand supported, in part, by the availability of planar waveguide fabrication foundries. Heterogeneously integrated 2D and 3D PICs have shown promising results in SDM coherent optical communications and optical beam steering, and we believe that these results will bring new applications in spatial imaging, light detection and ranging (LIDAR), parallel optical links, and other emerging areas.
References
Moore GE . Cramming more components onto integrated circuits. Reprinted from Electronics, volume 38, number 8, April 19, 1965, pp.114 ff. IEEE Solid-State Circuits Newsletter 2006; 3: 33–35.
Dennard RH, Gaenssle Fh, Yu HN et al. Design of ion-implanted MOSFETs with very small physical dimensions. IEEE Journal of Solid-State Circuits 1974; SC-9: 256–268.
Savchenkov AA, Matsko AB, Ilchenko VS et al. Optical resonators with ten million finesse. Optics Express 2007; 15: 6768–6773.
Hideaki M, Tadashi F, Takao K et al. Integration of a laser diode and a Twin FET. Japanese Journal of Applied Physics 1981; 20: 193.
Matsueda H . AlGaAs OEIC transmitters. Journal of Lightwave Technology 1987; 5: 1382–1390.
Gunn C . Fully integrated VLSI CMOS and photonics ‘CMOS Photonics’. 2007 IEEE Symposium on VLSI Technology; 12–14 Jun 2007; Kyoto, Japan; 2007: 6–9.
Emma PG, Kursun E . Is 3D chip technology the next growth engine for performance improvement? IBM Journal of Research and Development 2008; 52: 541–552.
Topol AW, Tulipe DCL, Shi L et al. Three-dimensional integrated circuits. IBM Journal of Research and Development 2006; 50: 491–506.
Thylén L, He S, Wosinski L et al. The Moore’s law for photonic integrated circuits. Journal of Zhejiang University SCIENCE A 2006; 7: 1961–1967.
Smit M, van der Tol J, Hill M . Moore’s law in photonics. Laser & Photonics Reviews 2012; 6: 1–13.
Guan B, Scott RP, Qin C et al. Free-space coherent optical communication with orbital angular, momentum multiplexing/demultiplexing using a hybrid 3D photonic integrated circuit. Optics Express 2014; 22: 145–156.
Scott RP, Guan B, Qin C et al. Free-space coherent optical communication demonstration using a 3D photonic integrated circuit device for orbital angular momentum multiplexing/demultiplexing. 39th European Conference and Exhibition on Optical Communication (ECOC 2013); 22–26 Sep 2013; London, UK; 2013: 1–3.
Chen H, Fontaine N, Ryf R et al. Design constraints of photonic-lantern spatial multiplexer based on laser-inscribed 3D-waveguide technology. Journal of Lightwave Technology 2014; 33: 1147–1154.
Chen H, van Uden R, Okonkwo C et al. Compact spatial multiplexers for mode division multiplexing. Optics Express 2014; 22: 31582–31594.
Fontaine NK . Integrated photonics and components for space-division multiplexing systems. 13th International Conference on Optical Communications and Networks (ICOCN 2014); 9–10 Nov 2014; Suzhou, China; 2014: 1–3.
Lin Z, Gendry M, Letartre X . Optical mode study of III—V-nanowire-based nanophotonic crystals for an integrated infrared band microlaser. Photonics Research 2014; 2: 182–185.
Luo Y, Chamanzar M, Apuzzo A et al. On-chip hybrid photonic–plasmonic light concentrator for nanofocusing in an integrated silicon photonics platform. Nano Letters 2015; 15: 849–856.
Song J, Luo X, Tu X et al. Three-dimensional (3D) monolithically integrated photodetector and WDM receiver based on bulk silicon wafer. Optics Express 2014; 22: 19546–19554.
Temporiti E, Minoia G, Repossi M et al. A 3D-integrated 25 Gbps silicon photonics receiver in PIC25G and 65nm CMOS technologies. 40th European Solid State Circuits Conference (ESSCIRC 2014); 22–26 Sep 2014; Venice Lido, Italy; 2014: 131–134.
Zhang ZY, Kleinert M, Maese-Novo A et al. Multicore polymer waveguides and multistep 45° mirrors for 3D photonic integration. IEEE Photonics Technology Letters 2014; 26: 1986–1989.
Gösele U, Tong Q-Y . Semiconductor wafer bonding. Annual Review of Materials Science 1998; 28: 215–241.
Lo YH, Bhat R, Hwang DM et al. Bonding by atomic rearrangement of InP/InGaAsP 1.5 μm wavelength lasers on GaAs substrates. Applied Physics Letters 1991; 58: 1961–1963.
Brouckaert J, Roelkens G, Van Thourhout D et al. Thin-film III-V photodetectors integrated on silicon-on-insulator photonic ICs. Journal of Lightwave Technology 2007; 25: 1053–1060.
Lo YH, Bhat R, Hwang DM et al. Semiconductor lasers on Si substrates using the technology of bonding by atomic rearrangement. Applied Physics Letters 1993; 62: 1038–1040.
Dudley JJ, Ishikawa M, Babic DI et al. 144°C operation of 1.3 μm InGaAsP vertical cavity lasers on GaAs substrates. Applied Physics Letters 1992; 61: 3095–3097.
Liang D, Bowers JE . Photonic integration: Si or InP substrates? Electronics Letters 2009; 45: 578–580.
Noda S, Tomoda K, Yamamoto N et al. Full three-dimensional photonic bandgap crystals at near-infrared wavelengths. Science 2000; 289: 604–606.
Sherwood-Droz N, Lipson M . Scalable 3D dense integration of photonics on bulk silicon. Optics Express 2011; 19: 17758–17765.
Shang K, Pathak S, Guan B et al. Si3N4 multilayer platform for photonic integrated circuits. CLEO: Science and Innovations 2015; 10–15 May 2015; San Jose, CA, USA; 2015.
Shang K, Pathak S, Liu G et al. Ultra-low loss vertical optical couplers for 3D photonic integrated circuits. Optical Fiber Communication Conference 2015; 22–26 Mar 2015; Los Angeles, CA, USA; 2015.
Raburn M, Liu B, Rauscher K et al. 3-D photonic circuit technology. IEEE Journal of Selected Topics in Quantum Electronics 2002; 8: 935–942.
Piels M, Bauters JF, Davenport ML et al. Low-loss silicon nitride AWG demultiplexer heterogeneously integrated with hybrid III-V/silicon photodetectors. Journal of Lightwave Technology 2014; 32: 817–823.
Parekh MS, Thadesar PA, Bakir MS . Electrical, optical and fluidic through-silicon vias for silicon interposer applications. IEEE 61st Electronic Components and Technology Conference (ECTC 2011); 31 May–3 Jun 2011; Lake Buena Vista, FL, USA; 2011: 1992–1998.
Eaton S, Cerullo G, Osellame R . Fundamentals of femtosecond laser modification of bulk dielectrics. Femtosecond Laser Micromachining 123, Osellame Roberto et al. Eds. Springer: Berlin/Heidelberg. 2012: 3–18.
Choudhury D, Macdonald JR, Kar AK . Ultrafast laser inscription: Perspectives on future integrated applications. Laser & Photonics Reviews 2014; 8: 827–846.
Thomson RR, Bookey HT, Psaila ND et al. Ultrafast-laser inscription of a three dimensional fan-out device for multicore fiber coupling applications. Optics Express 2007; 15: 11691–11697.
Nasu Y, Kohtoku M, Hibino Y . Low-loss waveguides written with a femtosecond laser for flexible interconnection in a planar light-wave circuit. Optics Letters 2005; 30: 723–725.
Nasu Y, Kohtoku M, Hibino Y et al. Waveguide interconnection in silica-based planar lightwave circuit using femtosecond laser. Journal of Lightwave Technology 2009; 27: 4033–4039.
Ródenas A, Martin G, Arezki B et al. Three-dimensional mid-infrared photonic circuits in chalcogenide glass. Optics Letters 2012; 37: 392–394.
Thomson RR, Birks TA, Leon-Saval SG et al. Ultrafast laser inscription of an integrated photonic lantern. Optics Express 2011; 19: 5698–5705.
Thomson R, Psaila N, Bookey H et al. Controlling the cross-section of ultrafast laser inscribed optical waveguides. In: Osellame R, Cerullo G, Ramponi R, editors. Femtosecond Laser Micromachining, vol. 123. Springer: Berlin/Heidelberg; 2012: 93–125.
Su TH, Scott RP, Djordjevic SS et al. Demonstration of free space coherent optical communication using integrated silicon photonic orbital angular momentum devices. Optics Express 2012; 20: 9396–9402.
Guan B, Scott RP, Fontaine NK et al. Integrated optical orbital angular momentum multiplexing device using 3D waveguides and a Silica PLC. CLEO: Science and Innovations 2013; 9–14 Jun 2013; San Jose, CA, USA; 2013.
Qin C, Guan B, Scott RP et al. Experimental demonstration of 3D elastic optical networking in space, time and frequency. CLEO: Science and Innovations 2015; 10–15 May 2015; San Jose, USA; 2015: SF1K.2.
Macdonald JR, Thomson RR, Beecher SJ et al. Ultrafast laser inscription of near-infrared waveguides in polycrystalline ZnSe. Optics Letters 2010; 35: 4036–4038.
Macdonald JR, Berry PA, Schelper KL et al. Directly written mid-infrared waveguides in zinc selenide. Advances in Optical Materials 2012; 1–3 Feb 2012; San Diego, CA, USA; 2012.
Kar AK . Ultrashort pulse inscription of photonic structures in ZnSe and GaAs for mid infrared applications. Air Force Research Laboratory Report AFRL-AFOSR-UK-TR-2010-0017; 2010.
Macdonald JR, Beecher SJ, Berry PA et al. Efficient mid-infrared Cr: ZnSe channel waveguide laser operating at 2486 nm. Optics Letters 38 2013, 2194–2196.
Lindenmann N, Balthasar G, Hillerkuss D . Photonic wire bonding: A novel concept for chip-scale interconnects. Optics Express 2012; 20: 17667–17677.
Guan B, Qin C, Scott RP et al. Polarization diversified integrated circuits for orbital angular momentum multiplexing. IEEE Photonics Technology Letters 2015; 27: 1056–1059.
Guan B, Qin C, Scott RP et al. Hybrid 3D photonic integrated circuit for optical phased array beam steering. CLEO: Science and Innovations 2015; 10–15 May 2015; San Jose, CA, USA; 2015.
Shang K, Pathak S, Guan B et al. Low-loss compact multilayer silicon nitride platform for 3D photonic integrated circuits. Optics Express 2015; 23: 21334–21342.
Shang K, Pathak S, Guan B et al. Tri-layer, vertical y-junction, Si2N4/SiO2 3D photonic integrated circuits with arbitrary splitting ratio. Optical Fiber Communication Conference 2016; 20–22 Mar 2016; Anaheim, CA, USA; 2016.
Acknowledgements
The authors acknowledge support in part by DARPA DSO Inpho grant HR0011-11-1-0005, ONR EW grant N000141310158, and NSF NeTS grant 1302719.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Yoo, S., Guan, B. & Scott, R. Heterogeneous 2D/3D photonic integrated microsystems. Microsyst Nanoeng 2, 16030 (2016). https://doi.org/10.1038/micronano.2016.30
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/micronano.2016.30