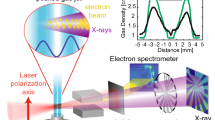
Abstract
Technology based on high-peak-power lasers has the potential to provide compact and intense radiation sources for a wide range of innovative applications. In particular, electrons that are accelerated in the wakefield of an intense laser pulse oscillate around the propagation axis and emit X-rays. This betatron source, which essentially reproduces the principle of a synchrotron at the millimeter scale, provides bright radiation with femtosecond duration and high spatial coherence. However, despite its unique features, the usability of the betatron source has been constrained by its poor control and stability. In this article, we demonstrate the reliable production of X-ray beams with tunable polarization. Using ionization-induced injection in a gas mixture, the orbits of the relativistic electrons emitting the radiation are reproducible and controlled. We observe that both the signal and beam profile fluctuations are significantly reduced and that the beam pointing varies by less than a tenth of the beam divergence. The polarization ratio reaches 80%, and the polarization axis can easily be rotated. We anticipate a broad impact of the source, as its unprecedented performance opens the way for new applications.
Similar content being viewed by others
Introduction
Over the past decade, ultrashort X-ray pulses have become an essential tool for exploring the dynamical properties of matter at the time scale of fundamental processes1. This field of research has quickly progressed since the emergence of X-ray free-electron lasers (X-FELs), which deliver intense and high-quality femtosecond X-rays2. Although FELs are invaluable tools, many of the experiments that are performed at the large-scale X-FEL facilities could be carried out with a less intense source. Hence, the development of more compact and cheaper sources should democratize the access to femtosecond X-rays. Among such alternative sources, the laser-driven betatron source is the brightest and most developed source in the X-ray regime3, 4. When produced with terawatt-class lasers, it delivers femtosecond X-rays in the few-keV energy range, with a divergence of some tens of milliradians and a peak brightness similar to that of third-generation synchrotrons5. Although it has been demonstrated that betatron radiation can be used to perform femtosecond X-ray diffraction6 and X-ray phase contrast tomography7, the source has been of limited use for other synchrotron-related techniques. For instance, X-ray absorption measurements are hindered by the significant shot-to-shot fluctuations8, and applications relying on magneto-optical phenomena would require polarized radiation9. Although first results related to polarized betatron radiation have been presented10, no laser-driven X-ray source with sufficient signal, stability and control of the polarization axis has been presented so far. In this article, a method to resolve this issue, using ionization-induced injection in a gas mixture, is presented.
Betatron radiation is most efficiently produced in the non-linear blowout regime11. Here the ponderomotive force of an intense femtosecond laser pulse propagating in an underdense plasma pushes electrons away from high-intensity regions and drives, in its wake, a relativistic plasma wave. The first period of this plasma wave consists of an ion cavity, which, due to its shape, is often referred to as a bubble12 (Figure 1). The electric fields inside this cavity reach up to teravolts per meter, and electrons trapped inside can be accelerated to hundreds of MeV at the millimeter scale13. In the transverse direction, similarly intense fields force the electrons into betatron oscillations. With a submillimeter oscillation length and a micron-scale oscillation amplitude, the resulting radiation is similar to the synchrotron emission in a wiggler. As its properties depend exclusively on electron orbits in the cavity4, the position and momentum of electrons at injection determine many radiation features14, 15.
Comparison of betatron oscillations in the transverse self-injection regime and the ionization-injection regime. (a, c) Schematic illustrations of the two injection mechanisms. In both cases, an intense femtosecond laser pulse, propagating in an underdense plasma, creates an ion cavity in its wake. For transverse self-injection a, electrons that get accelerated have to travel along the cavity sheath and enter the cavity at the back. Using Particle-in-cell simulations, it is found that these electrons originate from a ring-shaped region around the laser axis (b). In contrast, in the case of ionization-induced injection c, electrons are ionized inside the cavity, close to the maximum intensity of the laser. Injection can therefore occur longitudinally, and the initial position of trapped electrons is very different (d).
In most experiments, the injection of electrons relies on transverse self-injection. In this scheme, represented in Figure 1a, electrons travel along the sheath and enter the cavity at the back16. For perfect Gaussian laser pulses, the transversely self-injected electrons would originally be distributed homogeneously in an annular region around the pulse waist. However, when experimentally measured laser pulse profiles are used for simulations, it is found that such non-ideal pulses lead to more complex trapping patterns (Figure 1b). The position of injection cannot be controlled and strongly depends on the non-linear evolution of the laser as it propagates in the plasma. As a consequence, the electron injection and acceleration changes from shot to shot, and essential radiation properties such as the photon flux, spectrum, pointing and spatial profile fluctuate. Furthermore, radiation emitted from each electron is arbitrarily polarized, as transverse fields inside the bubble are radially symmetrical and there is no preferred direction of motion. This is different from conventional synchrotron sources, where the X-ray polarization can be controlled via the magnetic field in the insertion device. However, betatron radiation can be polarized if electrons are injected with a preferred direction of motion into the laser-wakefield accelerator. This was first demonstrated by tilting the pulse front of the laser pulse, resulting in asymmetric injection10. However, because this method still relied on self-injection, the X-ray signal varied from shot to shot. Furthermore, tilting the pulse front reduces the laser intensity and, thus, the efficiency of the accelerator.
To reliably produce polarized X-rays, it is therefore necessary to inject electrons in a controlled manner. One method to achieve this is to use a colliding laser pulse17. In this way, electron beams are produced more reliably, with tunable energy, low energy spread and small divergence. In turn, the beams contain low charge and have a small oscillation amplitude, and there is no preferred orientation for betatron oscillations. Thus, the radiation emission is stable, and its critical energy can be tuned, but the source is less bright and not polarized18.
We find that the above limitations can be overcome using another controlled injection technique, namely ionization-induced injection. This recently demonstrated injection mechanism19, 20 relies on the use of plasma formed from a gas mixture that consists mainly of a gas with a low atomic number (here, helium is used) and a small amount of gas with a high atomic number (here, 1% of nitrogen). The inner shell electrons of the high-Z species (the K-shell electrons of 7N in our case) are ionized close to the peak of the laser intensity envelope. Released almost at rest, they slip toward the back of the cavity, eventually receiving enough energy to get trapped21. As apparent from the schematic representation of ionization injection (Figure 1c), injection in this regime occurs essentially in the longitudinal direction. This is also seen in the simulations (Figure 1d), where a shallow halo corresponds to electrons trapped via transverse self-injection, whereas the broad spot around the laser axis corresponds to electrons from the K-shell of 7N. Ionization-induced injection is particularly known for its high stability20, 22, and as electrons are continuously injected, it also leads to a high beam charge (up to nC-level)20, 23. As stable, high-current electron beams are expected to produce bright, stable X-ray beams, the production of betatron radiation in this regime is studied.
Materials and methods
The experiment has been performed at the Laboratoire d’Optique Appliquée using the Salle Jaune system, a Ti:Sapphire laser operating at a 1 Hz repetition rate with a central wavelength λ0 of 813 nm. The laser delivers 1.2 J pulses at 28 fs Full width at half maximum (FWHM) duration. As depicted in the experimental setup (Supplementary Fig. S1), the laser beam is focused using an f/10 off-axis parabolic mirror. The laser distribution in the focal plane is close to Gaussian, with a waist w0 of 18 μm FWHM. This produces vacuum-focused intensities IL of the order of 3.5 × 1018 W cm−2, for which the corresponding normalized vector potential a0 is 1.3. The laser is initially polarized in the horizontal direction, but the polarization axis can be rotated using a λ/2 waveplate.
The plasma target is formed using a 3-mm diameter supersonic gas jet, which is placed in the focal plane of the laser beam. The electron plasma density for each shot is obtained by measuring the phase shift of a probe beam in a Nomarski-type interferometer. The results in this study are obtained using a mixture of helium (99%) and nitrogen (1%) and are compared to the results of acceleration in pure helium as a reference for self-injection. These reference data for pure helium are obtained at a density of ne=1.5 × 1019 cm−3. In contrast, no self-injection is observed at ne=1.0 × 1019 cm−3; thus, the results obtained with the mixed gas at this density are attributed to ionization-induced injection.
Electron beams are characterized using a magnet spectrometer, consisting of a 10-cm-long dipole magnet (1.1 T field strength), which deflects electrons onto a phosphor screen. The spectrometer covers energies from 80 to 400 MeV and also measures the beam divergence in the vertical direction. Scintillation light is imaged onto a 16-bit CCD camera, and the beam charge is deduced using the absolute calibration from Glinec et al24.
During the experiment, two different types of X-ray detectors are used. A gallium(III) oxide phosphor screen, fiber-coupled to a low-noise, 16-bit, 4-megapixel CCD camera (Princeton Quad-RO, Princeton instruments Inc., Trenton, NJ, USA), is used for beam profile and pointing measurements. The scintillator is protected by a 300-μm-thick beryllium filter. Placed 70 cm away from the source, the field of view is ~71 × 71 mrad2. The spectrum is obtained via single photon counting. For this, a direct-detection X-ray camera (Princeton Pixis, Princeton instruments Inc.) is placed on the laser axis at a distance of 9 m from the source. Taking the quantum efficiency and filters into account, the detector is sensitive from 4 to 14 keV. A 50-μm-thick Mylar filter is kept in front of both cameras. For polarization measurements, the X-ray beam is collimated using a polycapillary lens (f=300 mm) and sent onto an ADP (101) crystal. The reflected X-rays are sent toward the X-ray camera. The crystal reflectivity is maximal at 1.65 keV, corresponding to the Bragg energy.
Numerical modeling of the laser–plasma interaction is done using the fully electromagnetic three-dimensional Particle-In-Cell (PIC) code CALDER-CIRC25. It uses cylindrical coordinates (r, x) with Fourier decomposition along the poloidal direction for the discretization of the Vlasov–Maxwell equations. Supplementary to this, test particle simulations are used to interactively model the electron beam evolution in a spherical plasma cavity. Starting from the established analytical expressions for the fields inside a cavity, the code solves the equations of motion using a Runge–Kutta algorithm. For both PIC and test particle simulations, the calculated electron trajectories r(t) and momenta p(t) are used to calculate the radiation emission via the Liénard–Wiechert potentials. The total emitted intensity is obtained by taking the scalar product of the vector integral in the general expression of the radiation emitted by a moving charge in the polarization direction26.
Results and discussion
Experimental results
The accelerator is operated using the gas mixture, with an electron density of ne=1.0 × 1019 cm−3, and electron beams with an average charge of 40 pC are observed. As usual for ionization-induced trapping, electrons are continuously injected, and the resulting electron energy spectrum is broadband, with a cut-off energy of ~250 MeV (Supplementary Fig. S2).
The betatron signal from these electron beams is significantly different from the X-rays produced by the self-injected electron beams. Figure 2a shows the angular X-ray beam profile of four consecutive shots in pure helium (at ne=1.5 × 1019 cm−3) and in the gas mixture (at ne=1.0 × 1019cm−3). In pure helium, the X-ray beam spot presents complex structures, which vary from one shot to another in an uncontrolled way. These fluctuations of the spot shape are accompanied by significant variations of both the flux and spectrum of the radiation. Over a sample of 20 shots, the integrated signal within a radius of 5 mrad varies by 24%. In contrast, using the gas mixture, the beam stability is significantly improved, and fluctuations are reduced to 12%. Furthermore, the betatron emission is highly stable with respect to shape and position. As an illustration, Figure 2b represents the centroid position of 50 consecutive shots and the sum of the 50 angular beam profiles, which is almost indistinguishable from the individual shots shown in Figure 2a. The beam consistently has the same elliptical profile, with a larger mean divergence along the laser polarization axis (Θ||=33±1 mrad) than in the perpendicular direction (Θ⊥=12±1 mrad). The beam pointing (characterized by the standard deviation of the centroid position) varies within 1 mrad, which is ~10% of the beam divergence along the minor axis. The stability of the radiation spectrum is studied via single photon counting. Because the radiation spectrum is synchrotron-like27, a synchrotron spectrum is fitted to the experimental data for each shot (cf. Figure 3a). As shown in Figure 3b, the spectrum is very reproducible, with a critical energy Ec=6.7±0.5 keV (determined over 60 consecutive shots). In the reference case with pure helium, the critical energy is generally lower (Ec=6.5 keV), and the standard deviation is twice as large.
X-ray profiles for different gas compositions. (a) Angular profile of the X-ray beam for four consecutive shots in pure helium and in the gas mixture (He+1% N2). The color scale is the same for all images. (b) Integrated signal with the same area as in a for 50 consecutive shots in the mixed gas. Each green dot represents the centroid position for a single shot of the series. The standard deviation is 1 mrad, which corresponds to ~10% of the beam FWHM divergence. The FWHM divergences are 33 and 12 mrad along the two axes of the ellipse.
Spectral measurements: (a) typical spectrum, measured via single photon counting in the mixed gas. The data are fitted using a synchrotron function. (b) Critical energy for consecutive shots. Each circle represents the critical energy for one shot in pure helium, while crosses denote the mixed gas. Dashed lines show the average energy for helium (red) and the mixed gas (blue). The shaded area around these lines represents the standard deviation.
To verify that the orientation of the beam ellipse is correlated with the laser, the laser polarization axis is rotated. For both self-injection and ionization-induced injection, the average beam charge and energy are only weakly affected by this change. In the case of self-injection, the beam divergence is independent as well. However, for the electron beams resulting from ionization-induced injection, a larger divergence is measured along the laser polarization axis (Θ||=16 mrad FWHM), whereas the divergence is minimal in the perpendicular direction (Θ⊥=4 mrad FWHM). Like the electron beam, the X-ray beam profiles turn as well. As shown in Figure 4a–4d, the X-ray beam profiles maintain their elliptical shape, but the major ellipse axis rotates and is always aligned along the laser polarization axis.
Laser polarization dependence: (a–d) show the experimental betatron X-ray beam profiles obtained for four orientations of the laser polarization. The yellow line indicates the laser polarization axis. The red line in the figure represents the FWHM contour of the beam profile obtained from the test particle simulation. (e) X-ray signal reflected from an ADP (101) crystal for s- and p-polarization of the laser driver. Circles represent single shots, while the dashed lines represent the average signal for s-polarization (blue) and p-polarization (red).
The measurements indicate that electrons oscillate preferentially along the polarization axis of the laser; thus, the X-ray beam should also be partially polarized along this direction. To confirm this, the X-ray beam is sent to a polarization analyzer consisting of an ADP crystal at the Brewster angle, which reflects the beam onto an X-ray camera. Ideally, this reflection only consists of the perpendicular s-polarized component. As expected, the signal reaches its peak once the laser is s-polarized. When the laser polarization axis is rotated such that the laser is p-polarized, the reflected signal is minimal (cf. Figure 4e). The ratio of both values (2.9±0.8 for s-polarization; 1.0±0.3 for p-polarization) is used to calculate a polarization ratio Xp, which is defined as the percentage of intensity radiated along the laser polarization axis with respect to the total emitted intensity in both polarizations. With Xp=75±15%, the measurement shows that the radiation is indeed preferentially polarized along the laser polarization axis.
Numerical results and discussion
Electron beams produced by ionization-induced injection appear to be much less sensitive to laser intensity variations than those resulting from transverse injection, leading, in the former case, to the stable emission of X-rays. For deeper insight into the underlying physics, this phenomenon is investigated using PIC simulations. As initial conditions of the simulation, the experimentally measured focal spot is modeled using the modes m=0–5. The laser pulse duration is 30 fs, the laser peak intensity a0=2.0, and the numerical resolutions in the longitudinal and transverse directions are chosen to be Δx=0.2 k0−1 and Δr=1.5 k0−1, respectively. According to the conditions in the experiment, the simulations with pure helium are performed at a plasma density ne=1.5 × 1019 cm−3. The initial transverse position of trapped electrons is depicted in Figure 1b, with electrons originating from a ring-shaped region around the laser pulse. After acceleration, electrons are distributed without any apparent symmetry (Figure 5a), which is a result of the complexity of electron motion during transverse self-injection.
Simulation of the effect of a small laser energy change on the electron beam profile. (a, b) show the electron distribution after acceleration in pure helium; (c, d) show that in a mixture of 99% helium and 1% nitrogen. Left figures are for a0=2.0; right figures are for a0=1.95. A slight variation of laser intensity drastically changes the electron beam profile for transverse injection, while it remains unchanged for ionization injection. The laser is linearly polarized along the y axis (yellow line).
To reflect the measured shot-to-shot fluctuations of the laser system, another simulation is done for the same parameters, except for a slightly reduced laser intensity a0=1.95. The resulting injection distribution has a shape similar to that of the initial case (shown in Supplementary Fig. S3a). However, the electrons then follow trajectories close to the bubble sheath upon injection. The shape of this surface is strongly dependent on the laser and, in particular, on the distribution of the laser energy outside the central spot16. Moreover, transversely self-injected electrons cross the very end of the bubble, where the fields are the largest. This amplifies the effect of any cavity distortion on the trajectories of trapped electrons. As a result, the beam profile after acceleration is markedly different from the original distribution (Figure 5b), and the beam charge decreases by 60%. This high sensitivity to the laser parameters is the main reason for the unstable X-ray emission observed in the experiments.
Next, the target gas in the simulations is changed from pure helium to a mixture including 1% nitrogen. In this case, the laser propagation is still dominated by the helium contribution, but now electrons are mainly injected longitudinally due to the ionization-induced injection. Note that the plasma density is still ne=1.5 × 1019 cm−3, which is slightly higher than in the experiment but allows for better comparison of the two trapping mechanisms. As shown in Figure 5c, the electron bunch presents a smooth profile. The lack of inner structures within the spot, which are visible for self-injection, occurs because electrons travel inside the cavity and not along the bubble sheath. The fields inside the bubble are similar to those of an ion cavity and are not affected by small changes in the charge distribution at the bubble surface, that is, by the distortion of the laser spot. Electrons injected via this mechanism are therefore less sensitive to variations of the laser intensity: When a0 is reduced from 2.0 to 1.95, there is almost no noticeable effect on the electron distribution upon injection (cf. Supplementary Fig. S3b) nor on the final beam shape (cf. Figure 5d). In fact, the laser energy primarily affects the beam charge. In the above case, the laser energy is reduced by 6.25%, resulting in a charge decrease of 6.0%. This approximately linear relation between laser energy and beam charge is in accordance with the previous results related to ionization-induced injection23. The simulations thus explain the experimental observation of fluctuating electron beams in the transverse injection regime and stable acceleration in the regime of ionization-induced injection.
Furthermore, the electron beams in these simulations exhibit an elliptical profile, with their major axes oriented along the laser polarization. This is also in accordance with the experimental data. An examination of electron trajectories from the PIC simulations (Supplementary Fig. S4) helps explain this shape. In contrast to self-injected beams, electrons trapped via ionization-induced injection interact with the laser field while they travel through the cavity. This interaction presents itself as oscillations along the polarization axis. Depending on the initial position and the laser phase at ionization, different particle trajectories are observed. Electrons that experience a ponderomotive drift aligned with the oscillation direction will end up with the largest oscillation amplitude and contribute the most to the emitted radiation. Their oscillation plane is close to the polarization axis (Supplementary Fig. S4a and S4b) and can be tilted (Supplementary Fig. S4d). If the ponderomotive drift and the laser oscillations are not aligned, the electrons perform oscillations of small amplitude with random polarization. Taking into account the emission of the entire electron beam, it is found that the radiation is preferentially polarized along the laser polarization axis. The calculated polarization ratio Xp=90% is even higher than observed in the experiment. The effect is most pronounced for electrons ionized close to the center of the cavity, as the transverse wakefields act symmetrically on the electrons and reduce the polarization degree.
Betatron oscillations of electrons along a preferred direction result in the emission of an elliptical beam of (partially) polarized radiation14, a feature that is observed in both experiments and PIC simulations. As X-ray beam profiles are a direct signature of the electron orbits28, it should be possible to deduce the X-ray polarization ratio based on them. Test particle simulations are used to determine the electromagnetic field that reproduces the X-ray beam profile observed in the experiment. It is assumed that electrons are born at rest at the maximum intensity of the laser pulse. The conservation of canonical momentum implies that the transverse momentum gain from the laser field along the polarization direction ranges from zero to a029. The plasma wake is modeled as a spherical bubble with a background density ne=1 × 1019 cm−3. Electrons are initially distributed in a 1.2-μm diameter disk, with a uniform distribution of transverse momentum ranging from 0 to 3. Despite its simplicity, the model’s predictions are in accordance with the experimental data. As shown in Figure 4b, the FWHM of the calculated angular radiation profile aligns well with the observed beam profile. Furthermore, a polarization ratio Xp = 80±5% is estimated, which is in agreement with the data obtained using the polarization analyzer.
Conclusions
We have reported on synchrotron radiation from betatron oscillations of electrons in a laser-wakefield accelerator using ionization-induced injection. In our regime of operation, electrons are longitudinally injected into the wakefield, interact with the laser field and start to oscillate within the plane of laser polarization. The stability of the injection and subsequent acceleration result in the emission of X-rays in the few-keV range with unprecedented stability (10% pointing instability, 12% flux fluctuations, <10% beam-size variations and <7% critical energy variations). Furthermore, the interaction between the laser and electrons during injection provides a preferred oscillation plane. This leads to the emission of X-rays with a polarization ratio of up to 80%. The X-ray polarization axis can be turned by rotating the laser polarization axis while maintaining other beam parameters. In conclusion, the presented source combines, for the first time, high stability with easy tunability and should become a valuable tool for applications requiring polarized, broadband femtosecond X-rays.
Author contributions
AD, BM, SC, AD, JG, GG, EG, MH, MK, OL, CT and KTP conceived and realized the experiment. JPG, PR and AT operated the laser system. AD, BM, SC, CT and KTP analyzed the data. AL and KTP performed simulations. AD, SC, AL, VM, AR, CT and KTP discussed the results. AD, BM, CT and KTP wrote the paper.
References
Rousse A, Rischel C, Gauthier JC . Femtosecond X-ray crystallography. Rev Mod Phys 2001; 73: 17–31.
McNeil BWJ, Thompson NR . X-ray free-electron lasers. Nat Photonics 2010; 4: 814–821.
Rousse A, Ta Phuoc K, Shah R, Pukhov A, Lefebvre E et al. Production of a keV X-ray beam from synchrotron radiation in relativistic laser-plasma interaction. Phys Rev Lett 2004; 93: 135005.
Corde S, Ta Phuoc K, Lambert G, Fitour R, Malka V et al. Femtosecond x rays from laser-plasma accelerators. Rev Mod Phys 2013; 85: 1–48.
Kneip S, McGuffey C, Martins JL, Martins SF, Bellei C et al. Bright spatially coherent synchrotron X-rays from a table-top source. Nat Phys 2010; 6: 980–983.
Ta Phuoc K, Fitour R, Tafzi A, Garl T, Artemiev N et al. Demonstration of the ultrafast nature of laser produced betatron radiation. Phys Plasmas 2007; 14: 080701.
Wenz J, Schleede S, Khrennikov K, Bech M, Thibault P et al. Quantitative X-ray phase-contrast microtomography from a compact laser-driven betatron source. Nat Commun 2015; 6: 7568.
Schnell M, Sävert A, Uschmann I, Jansen O, Kaluza MC et al. Characterization and application of hard x-ray betatron radiation generated by relativistic electrons from a laser-wakefield accelerator. J Plasma Phys 2015; 84: 475810401.
Beaurepaire E, Bulou H, Scheurer F, Jean-Paul K . Magnetism and Synchrotron Radiation - New Trends. Berlin Heidelberg: Springer; 2010.
Schnell M, Sävert A, Uschmann I, Reuter M, Nicolai M et al. Optical control of hard X-ray polarization by electron injection in a laser wakefield accelerator. Nat Commun 2013; 4: 2421.
Lu W, Huang C, Zhou M, Mori WB, Katsouleas T . Nonlinear theory for relativistic plasma wakefields in the blowout regime. Phys Rev Lett 2006; 96: 165002.
Pukhov A, Meyer-ter-Vehn J . Laser wake field acceleration: the highly non-linear broken-wave regime. Appl Phys B 2002; 74: 355–361.
Malka V, Fritzler S, Lefebvre E, Aleonard MM, Burgy F et al. Electron acceleration by a wake field forced by an intense ultrashort laser pulse. Science 2002; 298: 1596–1600.
Ta Phuoc K, Corde S, Shah R, Albert F, Fitour R et al. Imaging electron trajectories in a laser-wakefield cavity using betatron X-ray radiation. Phys Rev Lett 2006; 97: 225002.
Thaury C, Guillaume E, Corde S, Lehe R, Le Bouteiller M et al. Angular-momentum evolution in laser-plasma accelerators. Phys Rev Lett 2013; 111: 135002.
Corde S, Thaury C, Lifschitz A, Lambert G, Ta Phuoc K et al. Observation of longitudinal and transverse self-injections in laser-plasma accelerators. Nat Commun 2013; 4: 1501.
Faure J, Rechatin C, Norlin A, Lifschitz A, Glinec Y et al. Controlled injection and acceleration of electrons in plasma wakefields by colliding laser pulses. Nature 2006; 444: 737–739.
Corde S, Thaury C, Ta Phuoc K, Lifschitz A, Lambert G et al. Mapping the X-ray emission region in a laser-plasma accelerator. Phys Rev Lett 2011; 107: 215004.
Pak A, Marsh KA, Martins SF, Lu W, Mori WB et al. Injection and trapping of tunnel-ionized electrons into laser-produced wakes. Phys Rev Lett 2010; 104: 025003.
McGuffey C, Thomas AGR, Schumaker W, Matsuoka T, Chvykov V et al. Ionization induced trapping in a laser wakefield accelerator. Phys Rev Lett 2010; 104: 025004.
Chen M, Sheng ZM, Ma YY, Zhang J . Electron injection and trapping in a laser wakefield by field ionization to high-charge states of gases. J Appl Phys 2006; 99: 056109.
Huang K, Li DZ, Yan WC, Li MH, Tao MZ et al. Simultaneous generation of quasi-monoenergetic electron and betatron X-rays from nitrogen gas via ionization injection. Appl Phys Lett 2014; 105: 204101.
Guillaume E, Döpp A, Thaury C, Lifschitz A, Goddet JP et al. Physics of fully-loaded laser-plasma accelerators. Phys Rev ST Accel Beams 2015; 18: 061301.
Glinec Y, Faure J, Guemnie-Tafo A, Malka V, Monard H et al. Absolute calibration for a broad range single shot electron spectrometer. Rev Sci Instrum 2006; 77: 103301.
Lifschitz AF, Davoine X, Lefebvre E, Faure J, Rechatin C et al. Particle-in-Cell modelling of laser-plasma interaction using Fourier decomposition. J Comput Phys 2009; 228: 1803–1814.
Jackson JD. Classical Electrodynamics, 3rd edn. New York: Wiley; 1998.
Fourmaux S, Corde S, Ta Phuoc K, Leguay PM, Payeur S et al. Demonstration of the synchrotron-type spectrum of laser-produced betatron radiation. New J Phys 2011; 13: 033017.
Ta Phuoc K, Corde S, Fitour R, Shah R, Albert F et al. Analysis of wakefield electron orbits in plasma wiggler. Phys Plasmas 2008; 15: 073106.
Moore CI, Ting A, McNaught SJ, Qiu J, Burris HR et al. A laser-accelerator injector based on laser ionization and ponderomotive acceleration of electrons. Phys Rev Lett 1999; 82: 1688–1691.
Acknowledgements
We acknowledge the Agence Nationale pour la Recherche through the FENICS Project No. ANR-12-JS04-0004-01, the Agence Nationale pour la Recherche through the FEMTOMAT Project No. ANR-13-BS04-0002, the X-Five project (Contract No. 339128), the LUCELX project (ANR-13-BS04-0011), the EuCARD2/ANAC2 EC FP7 project (Contract No. 312453), the GARC project 15-03118S and support from the European Union’s Horizon 2020 research and innovation program under Grant Agreement No. 654148 Laserlab-Europe.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Döpp, A., Mahieu, B., Lifschitz, A. et al. Stable femtosecond X-rays with tunable polarization from a laser-driven accelerator. Light Sci Appl 6, e17086 (2017). https://doi.org/10.1038/lsa.2017.86
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2017.86
Keywords
This article is cited by
-
Electro-optic 3D snapshot of a laser wakefield accelerated kilo-ampere electron bunch
Light: Science & Applications (2024)
-
Extended X-ray absorption spectroscopy using an ultrashort pulse laboratory-scale laser-plasma accelerator
Communications Physics (2024)
-
Femtosecond electron microscopy of relativistic electron bunches
Light: Science & Applications (2023)
-
Laser wakefield electron acceleration with PW lasers and future applications
Journal of the Korean Physical Society (2022)
-
Gamma-ray emission from wakefield-accelerated electrons wiggling in a laser field
Scientific Reports (2019)