Abstract
Ultrafast supercontinuum generation in gas-filled waveguides is an enabling technology for many intriguing applications ranging from attosecond metrology towards biophotonics, with the amount of spectral broadening crucially depending on the pulse dispersion of the propagating mode. In this study, we show that structural resonances in a gas-filled antiresonant hollow core optical fiber provide an additional degree of freedom in dispersion engineering, which enables the generation of more than three octaves of broadband light that ranges from deep UV wavelengths to near infrared. Our observation relies on the introduction of a geometric-induced resonance in the spectral vicinity of the ultrafast pump laser, outperforming gas dispersion and yielding a unique dispersion profile independent of core size, which is highly relevant for scaling input powers. Using a krypton-filled fiber, we observe spectral broadening from 200 nm to 1.7 μm at an output energy of ∼ 23 μJ within a single optical mode across the entire spectral bandwidth. Simulations show that the frequency generation results from an accelerated fission process of soliton-like waveforms in a non-adiabatic dispersion regime associated with the emission of multiple phase-matched Cherenkov radiations on both sides of the resonance. This effect, along with the dispersion tuning and scaling capabilities of the fiber geometry, enables coherent ultra-broadband and high-energy sources, which range from the UV to the mid‐infrared spectral range.
Similar content being viewed by others
Introduction
Since the very first observation of supercontinuum generation in bulk crystals or glasses in the 1970s1, 2, this phenomenon has been the subject of numerous investigations and represents one of the core physical problems in ultrafast nonlinear optics. Supercontinuum generation in optical fibers was first demonstrated in 19763, but the advent of photonic crystal fibers (PCFs) in 1999–20004, 5, 6, 7, 8 has revolutionized the field. PCFs reveal highly nonlinear interactions under the condition of single-mode guidance in a broad spectral range, having paved the way to establish unique light sources of temporally and spatially coherent white light, which can be considered as arbitrary wavelength and bandwidth sources of coherent radiation. Clearly, the importance of these sources is apparent in the wide range of applications including spectroscopy, microscopy (including beyond-diffraction-limit methods such as Stimulated Emission Depletion Microscopy (STED)9), attosecond metrology10, frequency comb technology11, 12, 13, 14, telecommunications, biophotonics15, and semiconductor inspection16.
A significant advantage in terms of achievable output energy of the supercontinuum and flexibility in controlling net dispersion was achieved by the invention of the hollow-core PCF and the Kagome fiber in particular17, 18. A Kagome fiber is a hollow-core PCF that combines the advantages of conventional hollow-core fibers (i.e., capillary19) with low transmission losses over a much broader spectral bandwidth than that of solid-core PCFs. Using gas as a nonlinear medium inside the hollow core, the energy of the generated supercontinuum has been increased by orders of magnitude due to the higher optical breakdown threshold of gases compared with solids and the ability to fine tune the pulse dispersion by changing the gas pressure. In addition, new regimes of supercontinuum generation at intensities close to the breakdown threshold, which involve the highly nonlinear process of gas ionization and enhance the short wavelength spectral region of the supercontinuum, have become accessible20, 21.
The physics of supercontinuum generation in PCF is complex and a subject of ongoing intensive research. A detailed review of the experimental and theoretical results can be found, for instance, in Ref. 22 and Ref. 23. The complexity of supercontinuum generation via femtosecond laser pulses in PCF can be divided into two distinct cases, which are determined by the sign of the group velocity dispersion (GVD) at the laser wavelength. In the normal dispersion regime (with a positive GVD), spectral broadening is governed primarily by self-phase modulation (SPM) and self-steepening24. In the case of anomalous dispersion (with a negative GVD), supercontinuum generation results from soliton dynamics, in particular from soliton self-compression, soliton fission and dispersive wave (i.e., Cherenkov radiation) emission22, 25, 26.
In this contribution, we report on efficient supercontinuum generation in a new type of hollow‐core PCF, the so‐called antiresonant hollow core fiber (ARHCF) design, which provides an additional degree of freedom in dispersion management and opens up a new regime of soliton dynamics by providing orders-of-magnitude change in group velocity dispersion within narrow spectral intervals with multiple zero-dispersion wavelengths. This novel fiber design allows for accurate and targeted spectral positioning of the strand resonances and an up-scaling of the core diameter without any drastic change to the dispersion landscape. Launching femtosecond pulses in an ARHCF filled with krypton gas in the spectral vicinity of the fundamental strand resonance (a resonance imposed by the glass ring surrounding the core section) allows for ultrabroadband supercontinuum generation (of more than three octaves) between the UV and near-infrared (NIR) with more than 10-μJ pulse output energy. Propagation in the fundamental mode is observed for all wavelengths. One key feature of the observed spectral broadening is its sudden onset with a slight increase in input pulse energy above a certain threshold. Our numerical simulations suggest that the mechanism behind the supercontinuum generation process results from coherent non-adiabatic soliton dynamics and multiple Cherenkov radiation generation events that are caused by strong structural resonance, which imposes a unique dispersion landscape that changes orders of magnitude several times from anomalous to normal with multiple zero-dispersion wavelengths.
Materials and methods
Antiresonant hollow core fibers
The fabrication of ARHCF used in the experiments relied on stacking six thin-walled capillaries (outer diameter 3.7 mm, wall thickness 0.4 mm) into a jacket tube and drawing this arrangement into cane and fiber (details of the fabrication procedure can be found elsewhere27).
The overall working principle of antiresonant hollow core fibers relates back to the fact that dielectric interfaces can show reflection values that are close to unity in the case of grazing incidence28. Even higher reflectivity values are obtained for two parallel interfaces (i.e., thin films) because interference effects strongly modify the interface reflection27. In the case in which the film thickness is of the order of the exciting wavelength, a resonance can cause light to tunnel through the glass strand. The spectral positions of these resonances are mainly defined by the strand thickness t:

In this Equation, the incident medium is air, n is the refractive index of glass, and m is the mode order29. Between two adjacent resonances, very high reflectivity values are obtained, which has been employed in antiresonant reflecting optical waveguides (ARROW), e.g., microfluidics30, and more recently within hollow core fibers31, 32. The supported leaky modes are effectively guided inside a thin ring of glass, whereby the modal attenuation scales inversely with the air core radius28. This is comparable to a capillary33 but with dramatically reduced losses (a few dBm−1 for core sizes of ∼ 50 μm instead of tens of dBm−1 for a capillary of the same diameter).
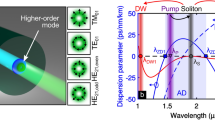
Because the group velocity dispersion depends on the second derivative of the propagation constant with respect to frequency, it is possible to vary the pulse dispersion properties massively near a strand resonance compared with simple capillaries or Kagome type fibers (Figure 1b and inset in Figure 1b). By adjusting the strand thickness, (see Equation (1)) and core size (Equations (2) and (3)), it is in fact possible to generate four zero-dispersion wavelengths within any desired spectral range in the transmission window of the fiber, which offers significant potential for dispersion engineering and power scaling beyond any of the existing schemes. Here, we show that dispersion engineering by choosing the correct position of the strand resonances offers a unique possibility for spectral tuning of supercontinuum generation, especially at IR wavelengths.
Essentials of ultrafast supercontinuum generation in structural resonance tuned gas-filled antiresonant hollow core fibers. (a) Conceptual scheme of the experiment. The inset image shows the antiresonant hollow core fiber used in the experiments (the white scale bar indicates a length of 20 μm). (b) Simulation of the frequency dependence of the group velocity dispersion of the fundamental mode in the ARHCF filled with krypton at a pressure of 6 bar (purple curve, strand resonance located at 1 μm; orange: corresponding gas-filled capillary dispersion when the strand resonance is neglected). The squares mark the zero group-velocity dispersion wavelengths. The inset is a close-up view of the GVD near the strand resonance. (c) Measured spectral distribution of the loss of the fundamental core mode of the antiresonant hollow core fiber, which is shown in a. The vertical blue dashed lines indicate the spectral positions of the resonances according to Equation (1), and the vertical red dashed line refers to the central wavelength of the femtosecond pump laser.
Experiments
The experiments were carried out using a femtosecond Ti:Sapphire laser system, delivering 80-fs pulses with energies up to 1 mJ at an 800-nm central wavelength and 1-kHz repetition rate (Spitfire, SpectraPhysics; the experimental setup is shown in Supplementary Fig. S1 in the Supplementary Information). The linearly polarized pulses that were emitted by the laser passed through a combination of a thin-film polarizer and a half-wave plate to control the input pulse energy between a few nJ and 50 μJ. The beam was collimated to a diameter of 12 mm and coupled into the core of the ARHCF (core diameter: 50 μm, sample length: 250 mm, inset of Figure 1) using a lens (focal length: 200 mm, focal beam diameter: 17 μm). A transmission efficiency of 65% was determined for the evacuated fiber. This value remained constant in the entire range of gas pressures and laser energies used in the experiments. The fiber input and output were mounted inside independent gas cells, which allowed either a constant gas pressure along the fiber or a pressure gradient. The output emission, which was attenuated by reflection from a wedge, was focused onto the entrance slits of three different spectrometers: two silicon CCD spectrometers (Ocean Optics USB4000-UV-VIS and USB2000+) for characterization in the UV and VIS spectral range and an InGaAs CCD spectrometer (Ocean Optics NIRQuest512) for the NIR spectral range. This combination of spectrometers allowed spectral characterization between 200 nm and 1.7 μm, which was confirmed by a control experiment with an entirely empty fiber, and showed only one signal at∼800 nm. The spectra were recorded at different integration times to ensure consistency and were stitched together by comparing the overlapping regions with similar spectral features to precisely record all the spectral features. Each individual spectrum was corrected for the spectral distribution of the respective spectrometer sensitivity. The output beam profiles at different wavelengths were recorded using a suitable combination of narrowband interference filters and cameras (UV/VIS: LaserCam-HR, Coherent GmBH with BeamView software; NIR: InGaAs ABS GmbH, IK-1513) placed at a distance of ≈120 mm from the fiber end.
Numerical simulations
For the simulations, we numerically solved the Unidirectional Propagation Pulse Equation (UPPE) in the frequency domain34:

Here,  is the spectral amplitude,
is the spectral amplitude,  is the Fourier transform operator, E (t, z) is the real electric field in the laser pulse, k (ω, p) is the wave vector determined by the dispersion relation where the pressure dependence of refractive index of the gas is described by
is the Fourier transform operator, E (t, z) is the real electric field in the laser pulse, k (ω, p) is the wave vector determined by the dispersion relation where the pressure dependence of refractive index of the gas is described by

In this Equation, p0 is the normal atmospheric pressure, n0 is the refractive index of gas at atmospheric pressure calculated using the Sellmeier Equation for Kr35, ν is the velocity of a reference frame chosen for convenience of simulations, and χ3 is the third order susceptibility, which is assumed to be instantaneous and, hence, frequency independent.
Results and discussion
Experimental results
The conceptual scheme of the experiment is shown in Figure 1a. The fiber used in the experiments consists of a central hollow core (diameter: 50 μm, inset of Figure 1a) surrounded by a thin silica ring that is supported by a series of connecting bridges (total fiber outer diameter, 125 μm). The small thickness of strands (average thickness, 495 nm) leads to a fundamental resonance (m=1) at ∼ 1.02 μm (Figure 1b), which is on the long wavelength-side of the central wavelength of the ultrafast laser used (0.8 μm). Cut-back measurements reveal a series of transmission bands with losses of between 5 and 10 dBm−1 across the UV, VIS and NIR spectral domains. Insufficient spectral density of the light source used (halogen lamp) prevents us from quantifying the loss below 350 nm, whereas the raw data indicate two more transmission bands with a minimum transmission wavelength of 220 nm. It is important to note that the fiber used reveals a variation of the strand thickness of ∼ 10%, which results from various fabrication issues, and which broadens the strand resonances (Figure 1c).
The dependence of spectral broadening of the 80-fs laser pulses at an 800-nm wavelength on the output pulse energy in the case of the ARHCF homogenously filled with krypton at 6 bar is shown in Figure 2b–2f. A sudden onset of spectral broadening is clearly visible at an ∼ 6.5-μJ output energy (Figure 2d), which evolves into a multi-octave-spanning supercontinuum that extends from ∼ 200 nm to 1.4 μm at an output pulse energy of 12.1 μJ. It is remarkable that a few-hundred nanometer spectral broadening is observed with only a 25% increase in the output energy (Figure 2d–2e). At 6.5 μJ of the output energy, broadening from 200 to 900 nm is observed, whereas the signal in the NIR is below the noise limit of the near-infrared spectrometer. An additional 20% increase in the input energy triggers dramatic spectral broadening towards the IR spectral range (Figure 2c–2d). A further increase in the input pulse energy mainly leads to an increase in the supercontinuum spectral density. With a constant pressure in the fiber, the maximum achieved output energy for the 3-octave-spanning supercontinuum is 12.1 μJ with a 19 μJ input energy. Higher input energies lead to significant ionization of the gas at the fiber input and damage to the fiber structure. At the maximum output energy that is used in the experiments with a constant gas pressure, measurements of the far-field beam profiles confirm fundamental mode propagation at all wavelengths of the supercontinuum (Figure 2n–2p). To confirm that the glass strands do not contribute to the spectral broadening as an additional nonlinear source, we performed experiments under the same conditions but with the fiber evacuated down to 10 s of mbar. The resulting spectral distribution of the output intensity in this case was essentially identical to that of the pulse input spectrum.
Measured spectral distribution of the output light after using a krypton-filled hollow core fiber at various output pulse energies (given in the plots). (a) Antiresonant fiber including a pressure gradient (low-pressure side facing input, pressure at output: 6 bar). (b)-(f) Homogenously filled fiber at a pressure of 6 bar. (g)-(p) Far field images (in false colors) of the output mode at various wavelengths for an output energy of 12.1 μJ (at a constant pressure) are shown on the right side of the figure (numbers indicate the central wavelengths (in nm) of the bandpass filters).
To overcome gas ionization at the fiber input and increase the energy of supercontinuum further, a differential gas pumping setup was used, keeping the input side of the fiber under vacuum (10 s of mbar) and maintaining a high gas pressure (of up to 6 bar) at the output end. This gradient gas pressure ensures that a dense gas plasma at the fiber input is avoided and enables higher energies to be coupled in. Additionally, precise focusing of the input beam avoids any direct damage of the fiber input by the focused laser beam and enables long term operation with no degradation in the output beam quality. This configuration yields similar spectral broadening at the short wavelength side of the spectrum for roughly double the coupled energy, but with an extended spectral broadening towards the NIR with the largest wavelength being 1.7 μm at an output pulse energy of 23 μJ (Figure 2a). It is worth mentioning that the high modal loss associated with the strand resonances (Figure 1b) is effectively suppressed for the highest input energies (yellow bars in Figure 2a and 2b), which indicates that the nonlinear process of frequency conversion is able to fill the high-loss spectral regions efficiently36. At maximum spectral broadening, we estimate a nearly 75% energy in the IR (>700 nm), ~24% in the VIS (400–700 nm) and ~1% in the UV (<400 nm). Both the linear dependence of input and output energy and estimation of the plasma density using the Popov-Perelomov-Terentiev Equation37 for the ionization rate suggest that ionization plays an insignificant role in our experimental conditions for input energies of at least up to 20 μJ. For the highest input energy of 35 μJ (corresponding to an output energy of 23 μJ energy (red curve in Figure 2a)), the relative plasma density increases to ≈2%, and nonlinear effects related to gas ionization (e.g., spectral blueshift) may play a role in the process of spectral broadening.
Numerical analysis
To reveal the physical origin of the observed broadening we performed nonlinear pulse propagation simulation using the UPPE34, assuming that the light of the pump at all generated wavelengths is propagated in a single mode along the entire length of the fiber. To calculate the modes and modal effective mode index, we also performed finite element simulations for the ARHCF structure used in the experiments32. Far from the strand resonance, the modal dispersion of the fundamental mode can be fitted well using the dispersion relation of a gas-filled HCF (i.e., capillary)33; this concept was used for simulating the nonlinear pulse propagation in Kagome fibers21:

where the angular frequency is ω, the gas pressure is p, the pressure-dependent refractive index of the gas is ng (at a constant temperature), the first root of the zero-order Bessel function is u11≈2.405, the core diameter is d and the vacuum speed of light is c.
To simulate the influence of strand resonance on the supercontinuum generation process, we modified the dispersion relation (2) as

where the coefficients a and b are calculated from fitting the effective mode index in the vicinity of the resonance by a Lorentzian function (a=2.05 × 109 s−1, b=9.4 × 1025 s−2). The resulting spectral distributions of the GVD for a Kagome fiber (orange curve) and for our ARHCF (purple curve) are shown in Figure 1b. The pulse propagation simulations assume the following conditions: 80 fs, 12 μJ laser pulses at a wavelength of 0.8 μm propagating in the 20-cm long ARCHF (core diameter: 50 μm) filled with Kr under 6 bar of constant pressure; these parameters are similar to the experimental conditions. For simplicity, we did not assess propagation losses. The wavelength of the fundamental strand resonance is chosen to be 1 μm, which approximately corresponds to the center of the measured NIR resonance band (Figure 1c).
Discussion
A direct comparison of the nonlinear pulse propagation simulations of the krypton-filled ARHCF with a Kagome fiber (with equivalent core diameters) clearly shows the profound influence of the strand resonance on the bandwidth of the generated light. In the Kagome case, monotonous spectral broadening that is driven by SPM, self-steepening, and optical wave breaking38 (see Supplementary Fig. S4 in the Supplementary Information) is observed, yielding a maximum bandwidth of approx. 900 nm for a 20-cm long fiber (Figure 3c).
Nonlinear pulse propagation simulations in ARCHF and Kagome-type fibers. (a) Spectral intensity distribution at various positions inside the ARHCF (core diameter of 50 μm) with the dispersion profile shown in Figure 1b. The vertical dashed line indicates the strand resonance, and the Cherenkov radiation bands are labeled by CR. The colors refer to the different intensity values defined by the top left color bar (logarithmic scale, normalized to unity). (b) Corresponding plot of the temporal evolution (top right color bar, linear color scale). Corresponding spectral and temporal distributions for a Kagome-type HCF with the same core diameter as the discussed ARHCF are shown in (c) and (d). The OWB label stands for optical wave breaking. The vertical dashed line in c indicates the ZDW. For all plots, ω0 refers to the central frequency of the initial pulse (2π c0/ω0=800 nm).
By contrast, the ARHCF shows a three-octave-spanning broadening that extends from 200 nm (ω/ω0=4) towards more than 2 μm (ω/ω0<0.4) with a sudden dramatic increase in the broadening rate (Figure 3a). Initially, the pulse propagates in a weakly anomalous dispersion regime and undergoes strong self-phase modulation and self-compression (Figure 3a), pushing the red frequency components of the pulse into the highly dispersive domain close to the strand resonance, shortening the fission length (given by Lfiss∝β2 (−1/2))22 and thus causing the pulse to break up into soliton-like temporally confined waves. After that break-up, the self-phase modulation of the main pulse towards the resonance stops. This effect has previously been predicted in simulations39 and is commonly referred to as soliton stabilization40. This process is accompanied by a dramatic emission of energy in the form of multiple phase-matched resonant Cherenkov radiation bands on the short wavelength side of the spectrum at a propagation distance of ∼ 7 cm (see Supplementary Fig. S3 in the Supplementary Information). In addition, the dispersion characteristic of the resonance allows for phase-matching to a second Cherenkov radiation band at propagation distances of beyond 10 cm, which leads to efficient energy transfer across the resonance into another anomalous dispersion regime at a longer wavelength, i.e., into the near IR (see Supplementary Fig. S3). The energy transfer processes towards shorter and longer wavelengths agree with the corresponding Cherenkov radiation phase-matching calculations (see Supplementary Fig. S5a in the Supplementary Information).
Based on the current research, Modulation Instabilities (MI) do not contribute to the light generation process for two reasons. First, the corresponding MI phase-matching curves (see Supplementary Fig. S5b in the Supplementary Information) do not match any of the observed waveforms, either in their spectral evolutions (Figure 3a) or in their spectrograms (see Supplementary Fig. S3 in the Supplementary Information). Second, MI are well-known to yield low pulse-to-pulse spectral stability, i.e., coherence. In this instance, the initial soliton number was calculated to be 16 (at a 12-μJ pulse energy), which is close to the empiric coherence limit introduced by Dudley et al. (i.e., N<15, Ref. 22) at which MI start to become dominant. For the gas-filled ARHCF discussed here, simulations that include phase-noise confirm that noise-driven MI do not influence the broadening process, because unity first-order coherence across the entire generated bandwidth after the main broadening events is observed (see Supplementary Fig. S2b in the Supplementary Information). Thus, the strong increase of the group velocity dispersion towards the resonance promotes coherent fission of solitonic waveforms before MI can occur in our case.
With further propagation, the solitary waves close to the resonance are strongly delayed by third-order dispersion41, which causes further energy transfer to resonant Cherenkov radiation and multiple parametric mixing processes that involve both solitary waves and Cherenkov radiation (e.g., clearly visible in the spectro-temporal representations in Supplementary Fig. S3 at a propagation distance of 7 cm); this extends the spectral bandwidth to a total spectral coverage of more than three octaves. It is important to mention that due to the lack of resonances, the spectral broadening in the Kagome-type fiber geometry investigated here occurs at much longer propagation distances, and energy transfer towards the UV can only be achieved with a significantly lower efficiency (see Figure 3c).
In contrast to the simulations, the implemented fiber exhibits multiple resonances, which may allow for cascaded phase-matching processes even further into the UV region. However, it is important to note that the resonances also feature large losses with an increasing effective mode area and thus a reducing nonlinearity when approaching the resonance40. The associated solitary waves are spectrally trapped near the resonance (i.e., experience a stabilization effect40) and may lose peak power comparably fast, which may be the reason for the reduced conversion efficiencies of cascaded effects and the smaller spectral bandwidth measured in the experiment.
It is important to note that even though our simulations only include one strand resonance, we obtain a good qualitative match between the simulations and our experimental results, which reveals the dramatic impact of a single strong resonance on nonlinear pulse propagation. Therefore, our calculations provide the first insights into the sophisticated nonlinear processes that are promoted by strongly varying group velocity dispersions close to the resonance, which effectively provides a large number of phase-matching opportunities for Cherenkov radiation regardless of the dispersion away from the resonance even in case of dispersion variations not considered in our model, e.g., induced by additional resonances.
Conclusions
In this contribution, we introduce the concept of modal dispersion engineering in noble gas-filled antiresonant hollow core fibers via structural strand resonances, which offers a new degree of freedom to design sophisticated dispersion landscapes and enables the generation of multiple octave supercontinua that span from deep UV wavelengths towards the near infrared with high spectral density. By launching femtosecond pulses into a krypton-filled fiber with submicron silica strands of a predefined thickness adjacent to the gas-filled core, we observe three‐octave-spanning output spectra at output pulse energies of 23 μJ. The experiments show a maximal broadening from the UV (200 nm) to ∼ 1.7 μm using differential gas pumping with a fundamental-mode-type output mode at all generated wavelengths. One striking feature of the generated spectra is the filling up of the high-attenuation domains of the antiresonant fiber, which diminishes the effect of strand-induced loss and leads to smooth spectra overall.
Qualitative agreement between the experiments and the nonlinear pulse propagation simulations has been achieved, which shows similar spectral behavior particularly at short wavelengths. The simulations show that the key to understanding the observed broadening is the strongly varying group velocity dispersion in the spectral vicinity of the fundamental strand resonance, which outperforms the dispersion of the gas and allows fundamentally new dispersion landscapes to be accessed. The non-adiabatically changing dispersion leads to an accelerated fission process of soliton-like waveforms, which is accompanied by the emission of multiple phase-matched resonant Cherenkov radiation bands on both sides of the structural resonance. Additionally, we expect a further extent of the spectrum by parametric wave mixing between solitary waves and Cherenkov radiation and a cascade of similar phase-matched processes due to the influence of higher-order structural resonances.
Future research will provide a deeper understanding of the nonlinear broadening effect using strand resonance coupling, with the final aim of reaching either deep-UV or mid-IR wavelengths, the latter of which was already indicated in our simulations. Due to its unique spectral broadness and scalability potential, we expect our concept to be highly relevant in application-driven areas such as wide-field spectroscopy, spectrally resolved imaging, metrology and biophotonics.
References
Alfano RR, Shapiro SL . Emission in the region 4000 to 7000 Å via four-photon coupling in glass. Phys Rev Lett 1970; 24: 584–587.
Alfano RR, Shapiro SL . Observation of self-phase modulation and small-scale filaments in crystals and glasses. Phys Rev Lett 1970; 24: 592–594.
Lin C, Stolen RH . New nanosecond continuum for excited-state spectroscopy. Appl Phys Lett 1976; 28: 216–218.
Ranka JK, Windeler RS, Stentz AJ . Visible continuum generation in air–silica microstructure optical fibers with anomalous dispersion at 800 nm. Opt Lett 2000; 25: 25–27.
Wadsworth WJ, Knight JC, Ortigosa-Blanch A, Arriaga J, Silvestre E et al. Soliton effects in photonic crystal fibres at 850 nm. Electron Lett 2000; 36: 53–55.
Wadsworth WJ, Ortigosa-Blanch A, Knight JC, Birks TA, Man TPM et al. Supercontinuum generation in photonic crystal fibers and optical fiber tapers: A novel light source. J Opt Soc Am B 2002; 19: 2148–2155.
Knight JC . Photonic crystal fibres. Nature 2003; 424: 847–851.
Russell P . Photonic crystal fibers. Science 2003; 299: 358–362.
Wildanger D, Rittweger E, Kastrup L, Hell SW . STED microscopy with a supercontinuum laser source. Opt Express 2008; 16: 9614–9621.
Wirth A, Hassan MT, Grguraš I, Gagnon J, Moulet A et al. Synthesized light transients. Science 2011; 334: 195–200.
Diddams SA, Jones DJ, Ye J, Cundiff ST, Hall JL et al. Direct link between microwave and optical frequencies with a 300 THz femtosecond laser comb. Phys Rev Lett 2000; 84: 5102–5105.
Jones DJ, Diddams SA, Ranka JK, Stentz A, Windeler RS et al. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science 2000; 288: 635–639.
Holzwarth R, Udem T, Hänsch TW, Knight JC, Wadsworth WJ et al. Optical frequency synthesizer for precision spectroscopy. Phys Rev Lett 2000; 85: 2264–2267.
Newbury NR . Searching for applications with a fine-tooth comb. Nat Photonic 2011; 5: 186–188.
Tu HH, Boppart SA . Coherent fiber supercontinuum for biophotonics. Laser Photonics Rev 2013; 7: 628–645.
Byeon CC, Oh MK, Kang HS, Ko DK, Lee JM et al. Coherent absorption spectroscopy with supercontinuum for semiconductor quantum well structure. J Opt Soc Korea 2007; 11: 138–141.
Couny F, Benabid F . Light PS. Large-pitch Kagome-structured hollow-core photonic crystal fiber. Opt Lett 2006; 31: 3574–3576.
Wang YY, Wheeler NV, Couny F, Roberts PJ, Benabid F . Low loss broadband transmission in hypocycloid-core Kagome hollow-core photonic crystal fiber. Opt Lett 2011; 36: 669–671.
Nisoli M, De Silvestri S, Svelto O, Szipöcs R, Ferencz K et al. Compression of high-energy laser pulses below 5 fs. Opt Lett 1997; 22: 522–524.
Mak KF, Travers JC, Hölzer P, Joly NY . Russell PSJ. Tunable vacuum-UV to visible ultrafast pulse source based on gas-filled Kagome-PCF. Opt Express 2013; 21: 10942–10953.
Russell PSJ, Hölzer P, Chang W, Abdolvand A, Travers JC . Hollow-core photonic crystal fibres for gas-based nonlinear optics. Nat Photonics 2014; 8: 278–286.
Dudley JM, Genty G, Coen S . Supercontinuum generation in photonic crystal fiber. Rev Mod Phys 2006; 78: 1135–1184.
Dudley JM, Taylor JR . Supercontinuum Generation in Optical Fiber. Cambridge: Cambridge University Press; 2010.
Heidt AM . Pulse preserving flat-top supercontinuum generation in all-normal dispersion photonic crystal fibers. J Opt Soc Am B 2010; 27: 550–559.
Chemnitz M, Wei JX, Jain C, Rodrigues BP, Wieduwilt T et al. Octave-spanning supercontinuum generation in hybrid silver metaphosphate/silica step-index fibers. Opt Lett 2016; 41: 3519–3522.
Granzow N, Schmidt MA, Chang W, Wang L, Coulombier Q et al. Mid-infrared supercontinuum generation in As2S3-silica “nano-spike” step-index waveguide. Opt Exp 2013; 21: 10969–10977.
Hartung A, Kobelke J, Schwuchow A, Wondraczek K, Bierlich J et al. Double antiresonant hollow core fiber–guidance in the deep ultraviolet by modified tunneling leaky modes. Opt Express 2014; 22: 19131–19140.
Zeisberger M, Tuniz A, Schmidt MA . Analytic model for the complex effective index dispersion of metamaterial-cladding large-area hollow core fibers. Opt Express 2016; 24: 20515–20528.
Litchinitser NM, Dunn SC, Steinvurzel PE, Eggleton BJ, White TP et al. Application of an ARROW model for designing tunable photonic devices. Opt Express 2004; 12: 1540–1550.
Bernini R, Campopiano S, Zeni L . Design and analysis of an integrated antiresonant reflecting optical waveguide refractive-index sensor. Appl Opt 2002; 41: 70–73.
Belardi W, Knight JC . Hollow antiresonant fibers with low bending loss. Opt Express 2014; 22: 10091–10096.
Hartung A, Kobelke J, Schwuchow A, Bierlich J, Popp J et al. Low-loss single-mode guidance in large-core antiresonant hollow-core fibers. Opt Lett 2015; 40: 3432–3435.
Marcatili EAJ, Schmeltzer RA . Hollow metallic and dielectric waveguides for long distance optical transmission and lasers. Bell Syst Tech J 1964; 43: 1783–1809.
Couairon A, Brambilla E, Corti T, Majus D, Ramírez-Góngora O et al. Practitioner’s guide to laser pulse propagation models and simulation. Eur Phys J Spec Top 2011; 199: 5–76.
Dalgarno A, Kingston AE . The refractive indices and Verdet constants of the inert gases. Proc Roy Soc A Math, Phys Eng Sci 1960; 259: 424–431.
Präkelt A, Wollenhaupt M, Sarpe-Tudoran C, Assion A, Baumert T . Filling a spectral hole via self-phase modulation. Appl Phys Lett 2015; 87: 121113.
Perelomov AM, Popov VS, Terentev MV . Ionization of atoms in an alternating electric field. J Exptl Theoret Phys 1966; 50: 1393–1409.
Heidt AM, Hartung A, Bartelt H . Generation of ultrashort and coherent supercontinuum light pulses in all-normal dispersion fibers. In: Alfano RR, editor. The Supercontinuum Laser Source: The Ultimate White Light. New York: Springer; 2016, pp247–280.
Vanvincq O, Kudlinski A, Bétourné A, Quiquempois Y, Bouwmans G . Extreme deceleration of the soliton self-frequency shift by the third-order dispersion in solid-core photonic bandgap fibers. J Opt Soc Am B 2010; 27: 2328–2335.
Pureur V, Dudley JM . Nonlinear spectral broadening of femtosecond pulses in solid-core photonic bandgap fibers. Opt Lett 2010; 35: 2813–2815.
Agrawal G . Nonlinear Fiber Optics. 5th edn. London: Academic Press; 2013.
Acknowledgements
Funding from the federal state of Thuringia (FKZ: 2012FGR0013 and FKZ: 2016FGR0051) and ESF is highly acknowledged. M. Z. acknowledges support from the Humboldt Foundation. R. S. acknowledges support from German Research Foundation (DFG) for funding through International Research Training Group (IRTG) 2101. M. C. acknowledges support from German Research Foundation (DFG) via the project SCHM2655/3-1.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Sollapur, R., Kartashov, D., Zürch, M. et al. Resonance-enhanced multi-octave supercontinuum generation in antiresonant hollow-core fibers. Light Sci Appl 6, e17124 (2017). https://doi.org/10.1038/lsa.2017.124
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2017.124
Keywords
This article is cited by
-
Probing molecules in gas cells of subwavelength thickness with high frequency resolution
Nature Communications (2024)
-
Energy transmittance of focused femtosecond pulses at different air pressures
Optoelectronics Letters (2023)
-
An achromatic metafiber for focusing and imaging across the entire telecommunication range
Nature Communications (2022)
-
Higher-order mode supercontinuum generation in dispersion-engineered liquid-core fibers
Scientific Reports (2021)