Abstract
In this work, we experimentally demonstrate for the first time the spontaneous generation of two-dimensional exciton-polariton X-waves. X-waves belong to the family of localized packets that can sustain their shape without spreading, even in the linear regime. This allows the wavepacket to maintain its shape and size for very low densities and very long times compared to soliton waves, which always necessitate a nonlinearity to compensate the diffusion. Here, we exploit the polariton nonlinearity and uniquely structured dispersion, comprising both positive- and negative-mass curvatures, to trigger an asymmetric four-wave mixing in momentum space. This ultimately enables the self-formation of a spatial X-wave front. Using ultrafast imaging experiments, we observe the early reshaping of the initial Gaussian packet into the X-pulse and its propagation, even for vanishingly small densities. This allows us to outline the crucial effects and parameters that drive the phenomena and to tune the degree of superluminal propagation, which we found to be in close agreement with numerical simulations.
Similar content being viewed by others
Introduction
X-waves (XWs)1, 2 are a specific type of nonspreading wave packet that maintain their transverse shape along a large field depth with respect to Gaussian beams or other packets. Another well-known class of nonspreading waves are solitons. However, the dispersion of solitons is constantly compensated by nonlinearity in the medium. Instead, XWs, as a type of nonspreading wave, are generally formed by Bessel beams and can maintain their shape in the absence of nonlinearity3. XWs are a topic of great interest in multiple fields, spanning from photonics to acoustics, and are relevant in any system that is governed by the wave equation. The first experimental demonstration of such optical waves employed a cw laser light4. These beams are not free from diffraction, but their transverse profile keeps its main peak well confined, whereas the weaker lateral peaks expand upon propagation. The same localization principle holds for pulsed XW packets that, in essence, are a polychromatic superposition of Bessel beams5.
Since the early 1990s, XWs have been extensively studied both theoretically and experimentally using nonspreading acoustic pulses by Lu and Greenleaf6, 7. Later, XWs were obtained with light by injecting sub-ps laser pulses across a dispersive material3, demonstrating the potential for signal transmission and imaging. Indeed, their application spans different systems1: medical ultrasonic scanning; optical coherence tomography; nondestructive evaluation of materials and defect identification, including free space optical and radio-based telecommunication systems; optical tweezers, such as accelerating or guiding beams; plasmonics near-field manipulation; microscopy; and signal transmission. In nanotechnology, the localized waves allow reliable production of high-quality beams, which are required for optical and electron-beam lithography with subdiffraction resolution8. Any of these experimental cases has relevance to, for example, realistic antennas truncated in time and space, and analytical solutions have been found for the finite energy content cases9, 10. Among their fascinating properties, it is worth mentioning that X-waves in vacuum also correspond to the simplest superluminal waveforms9, 10. This indicates that XWs can have an effective velocity higher than c, which emerges from the superposition of ordinary Bessel beams4, 5 and, at the same time, conform to the constraints of special relativity and the causality principle1.
Renewed interest in the XWs is also driven by their potential applicability in the field of atomic Bose-Einstein condensates (BEC)11 and dissipative polariton condensates12. Both of these systems bear deep similarity to the electromagnetic case because they can be described by nonlinear Schrödinger equations13, 14. Polariton XW solutions were predicted not only for microcavity polaritons12, but also in the case of Bragg polaritons by periodically embedding quantum wells directly into multilayer stacks15. In both cases, the XW solutions rely on the locally hyperbolic dispersion (that is, including both negative and positive curvatures). Several theoretical proposals have been developed on this topic as well as on the possibility to obtain spontaneous X-waves upon exploitation of the nonlinearities16, 17, 18, 19. Recently, a quantum description of XWs has been developed, highlighting the difference in the entanglement properties between externally imprinted and spontaneously generated states20. However, X-waves have not yet been imprinted or generated in a BEC.
Our work bridges X-wave concepts to hybrid fluids of light and matter. We report the first experimental self-generation of an XW packet in a two-dimensional (2D) exciton-polariton superfluid starting from an initial Gaussian photonic pulse. This effect has been achieved upon fine tuning of the polariton nonlinearity and proper balance of the positive/negative effective mass ratios along the transverse/longitudinal directions. Using ultrafast digital holography, the experiments show the initial pulse reshaping and propagating, which demonstrating its longitudinal localization down to vanishing densities of the packet. It is noteworthy that the 2D polariton geometry allows the axial XW density and phase profiles along the propagation direction to be determined. The optical access to the wavefunction phase allows highlighting some peculiar topological defects associated with the specific way we obtain the X-wave. Moreover, upon uniquely changing the initial amount of nonlinearity, we show a tunable superluminal peak speed with respect to the group velocity of the polariton system.
Microcavity exciton polaritons21, 22, 23, 24, 25, 26, 27 are bosonic particles that result from the mixing of two quasiparabolic modes, the quantum well (QW) excitons and the microcavity (MC) photons, with dispersions of highly unbalanced curvatures. The anticrossing feature of the bare modes, associated with the strong coupling regime, finally produces a highly nonparabolic shape for one of the new normal modes, namely, the lower polariton branch (LPB)28. In particular, the presence of an inflection point, representing both a maximum of the group velocity (vg=∂ω/∂k) and an inversion of the so called diffusive effective mass [mdiff=(∂2ω/∂k2)−1] (see Ref. 29), is the fundamental reason for the spontaneous XW formation. Polaritons also exhibit very strong nonlinearities30, 31 that are able to achieve superfluid regimes32, 33 that support quantized vortices34, 35, or lead to several patterns36, 37, 38, 39 and soliton state formations40, 41. However, we note that the XW, a solution that exists in the linear limit, is fundamentally different from the 2D bright solitons discussed in Refs 41, 42. In this case, localization was achieved in the so called bistability regime, in which the soliton wave packet was supported by an additional background pump. While the solitonic wave packets are well suited for polaritonic devices that utilize nonlinearity, such as logic gates or transistors43, they are inherently fragile against particle loss that is unavoidable in any photonic system. On the other hand, linearly localized solutions are fundamentally robust against losses and have potential applications in data transport between distant system components. This approach has been demonstrated to be efficient in overcoming performance bottlenecks in electronic signal processing44.
Materials and methods
Experimental methods
The experiments described here are performed on a GaAs/AlxGaAs MC composed of three QW enclosed by two distributed Bragg reflectors, the details of which can be found in Refs 45, 46. The positions inside the MC are set to have the QWs in the antinodes of the confined photonic field. The strong coupling of the two bare modes, the photonic (ψC) and excitonic (ψX) fields, leads to two new hybrid modes: the LPB and the upper polariton branch (UPB). This sample is also grown on a specifically doped GaAs substrate with a transparency window centered at 830 nm, which consequently allows operation in a transmission configuration. The sample is kept at a constant temperature of 10 K using a cryostat to avoid thermal ionization of excitons.
This experiment uses an ultrafast digital holography setup (described in Refs 45, 46), in which the emission signal is allowed to interfere with a homodyne, uniform, reference plane wave. The two beams are sent at slightly different incidence angles onto a charge-coupled device camera to collect the associated interference pattern. The resulting interferograms are analyzed with a digital fast Fourier transformation to obtain the amplitude (ψ) and the phase (φ) of the complex wavefunction in real space. A delay line on the reference optical path allows us to scan the signal with respect to time by changing the time delay of the reference. The temporal resolution of this technique is mainly limited by the 2.5 ps duration of the laser pulse, which allows selective excitation of the lower polariton mode upon proper tuning at ~836 nm. The time step was set to 0.5 ps.
The circular polarization is set in the excitation beam to generate only one spin population and consequently maximize the interactions. The same reshaping effects are obtained upon a double total population density when using a linearly polarized excitation beam. The pump spot is set with a FWHMx,y of 10 μm (FWHMkx,ky=0.6 μm−1 in reciprocal space), to facilitate the nonlinear scattering process in real space and have a wide enough spot size to cover the dispersion range of interest in k-space.
Numerical methods
To illustrate the dynamical X-wave formation and localization induced by the nonlinearity, we performed simulations starting from a Gaussian initial state Ψ(x,y)=1/(2πσ2) exp{−(x2+y2)/(2σ2)}, where σ=FWHM/(2sqrt(2ln2)) and FWHM is the full-width at half-maximum of the Gaussian spot. The GPE described in the text was solved numerically using the fourth-order Runge-Kutta method. The device parameters were as follows: mC=4.27 × 10−5 me, γC=0.2 ps−1, γX=0.2 ps−1, g=2 × 10−3 meV μm2, Δ=−0.55 meV and ΩR=5.4 meV. The details of the numerical method are described in Ref. 47. Numerical computations were performed with a Zeus cluster in the ACK ‘Cyfronet’ AGH computer center.
Results and discussion
Dispersion and effective masses
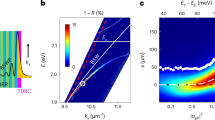
The high-quality Q factor of our microcavity indicates that the LPB and UPB modes are well separated with respect to their linewidths. The two modes can hence manifest their dispersions, observed upon collecting the off-resonance excited fluorescence as shown in Figure 1a. Here, we will focus our attention only on the LPB, which shows a strong nonparabolic behavior at higher k vectors. Further, experimental details can be found in the ‘Methods and Materials’ section. The 3D representation of the LPB dispersion surface E(kx,ky) is shown in Figure 1b in a region around the inflection point (kx~1.62 μm−1). In the figure, we highlight the nonparabolic characteristics by reporting two orthogonal crosscuts along the longitudinal direction (// blue curve, centered at ky=0) and along the transverse direction (⊥ red curve, at kx=2.15 μm−1). The noteworthy feature that can be appreciated from the 3D representation is the opposing curvature of the two slices around the inflection point.
Polariton dispersion. (a) Experimental dispersion under nonresonant pumping. The superimposed points (different colors) on the right side of the lower branch represent the polariton emission under resonant excitation at different momenta k, and the solid lines are theoretical fits. (b) 3D representation of the E(kx,ky) dispersion surface around the inflection point, highlighting the central longitudinal crosscut (blue line) and an exemplificative transverse one (red line). (c) First derivative (group velocity) of the dispersion along the propagation direction (//, blue) and the transverse direction (⊥, red). The black dots represent the experimental group velocities (retrieved by independent experiments on fluid dynamics). (d) Second derivative (inverse effective mass) of the dispersion along the propagation direction (//, blue), the transverse direction (⊥, red) and their difference (δ, green). The vertical black lines define the explored k region that maximizes the effective mass anisotropy.
Moving along the central longitudinal line, the dispersion geometry always corresponds to a null transverse velocity [∂ω/∂ky(kx,ky=0)]. The longitudinal group velocity instead grows to a maximum (1.5 μm ps−1) at the inflection point and decreases for larger, in-plane longitudinal momenta (kx), Figure 1c. At the same time, both the longitudinal and transverse curvatures of the dispersion surface change as a function of kx, as clearly illustrated in Figure 1d. In particular, the curvatures have opposite signs inside the investigated region (the explored range is denoted by dots or by vertical ticks in any of the four panels), which corresponds to opposing effective masses.
Polariton X-wave
We resonantly excite the polariton superfluid with 2.5 ps laser pulses tuned at ~836 nm and focused to a ~10 μm diameter spot. In Figure 2, we experimentally show the dynamics of the effect optimized using k=2.35 μm−1 and 75 μW of pumping power. Figure 2a displays the modulus, and Figure 2b shows the phase of the polariton X-wave packet. The time zero in the temporal evolution is set when the pump stops injecting polaritons, which are then free to evolve within their lifetime. Initially, the density distribution reveals a Gaussian shape with a rather homogeneous phase (with just a weak radial gradient associated with the beam curvature). However, after 10 ps, the X-wave shape can be clearly distinguished. At the successive t=20 and 30 ps snapshots, we can detect just a small vertical spread of the packet, but without a significant distortion in the shape. Notably, the longitudinal waist size remains essentially constant, despite the polariton lifetime being as short as ~10 ps45, 46.
Dynamical XW sequence. (a and b) Spatial distribution of the polariton wavefunction amplitude (a) and phase (b) at different time frames (t=−10, 0, 10, 20 and 30 ps). The t=0 corresponds to the end of pulse injection and consequently to the start of the free evolution. The phase map is represented with respect to the moving-packet’s frame of reference (see also Supplementary Movies 1 and 2). (c and d) Detailed maps of the amplitude (c) and phase (d) (t=27.5 ps), with a superposition of the relative in-plane momenta distribution (red arrows) and of the quantized vortices (blue and green circles). (e and f) The GPE simulated amplitude (e) and phase (f) maps at 27.5 ps for a 10-μm-wide pump spot and a wavevector of 2.55 μm−1. All the amplitude maps are normalized to their maximum at the specific time frame.
An interesting feature can be seen in the phase map of Figure 2b: the appearance of four quantized vortices, at the edges of the packet. These vortices are shown in detail in the maps of Figure 2c and 2d, overlapping the streamlines of the phase gradient (red arrows) and the dots of the phase singularities (blue and green arrow circles). The diagonally displaced vortex-antivortex pairs are an expression of the hyperbolic topology of the driving in-plane momenta. Indeed, as evident in the center of the packet, the flows are pushing the polaritons inwards along the propagation direction, which keeps the signal compact, and outwards in the transverse direction.
The dynamics of the polariton superfluid were successfully modeled within the mean field approximation by a set of coupled equations equivalent to the Gross-Pitaevskii Equation (GPE):

where mC is the effective mass of the microcavity photons, ΩR is the Rabi frequency coupling the photonic ψC and excitonic ψX fields, γC and γX are the associated decay rates and g is the nonlinear interaction term in the exciton component. Further details are given in the ‘Methods and Materials’ section. The results shown in Figure 2e and 2f, represent the amplitude and phase maps, respectively, at 27.5 ps, demonstrating strong agreement with the main experimental features. The modulation in the tail of the signal that can be seen in the theoretical predictions shown in Figure 2e and 2f, could be due to the interference with a weak nonlinear scattering to opposite kx states. This modulation may be not visible in the experimental data due to the achievable temporal resolution (2.5 ps limited by the reference pulse).
The opposite transverse and longitudinal effective masses force the GPE, which describes the polariton dynamics, to show a highly hyperbolic character. This behavior is crucial to sustain the X-wave phenomena, which demonstrates that the shape conservation does not rely on the nonlinearity, as in the case with solitons37, 41, but rather on the dispersion morphology. It was previously shown that an X-shaped initial profile can be a stationary solution of the linear GPE model12. We experimentally demonstrate that in a weakly nonlinear regime, an initial Gaussian state can be triggered to spontaneously evolve into a steady X-wave via an early four-wave mixing (FWM) process.
Nonlinear triggering
Although the nonlinearities play no role in the propagation and maintenance of the signal, they are crucial for the initial reshaping of the Gaussian pulse into the X-packet. Indeed, the choice of the initial spot size in real space (density FWHM ~10 μm) produces a proper extension in the reciprocal (momentum) space (FWHM ~0.6 μm−1), thus exploiting the negative curvature. The nonlinearity allows an asymmetric reshaping in momentum space based on the dispersion shape. Thus, an elongated spot in the reciprocal k-space is created along the direction of propagation, signifying a stronger confinement in real space.
To highlight the impact of the nonlinearities, the temporal dynamics at four different pumping powers are shown in Figure 3. At a low density, as shown in Figure 3a, the reshaping is absent and the signal spreads uniformly in both the longitudinal and transverse directions. However, an anisotropy in the intensity distribution between the longitudinal and transverse diffusions starts to appear when increasing the pump power, as shown in Figure 3b and 3c. At 75 μW, the reshaping reaches its optimum, shown in Figure 3d, and the packet shows a very well-defined X-shape, together with a small circular tail. Above this power, the dynamics enter into a strongly nonlinear regime (between 100 and 500 μW), where the redistribution due to high densities involves radial counterflows, which reshape the signal beyond a recognizable X-packet. Such a regime occurs just before the onset of the dynamical nonlinearity inversion, leading to the real space collapse described in Ref. 37.
Tuning of the packet reshaping. (a–d) Each row corresponds to a different power and the optimal injection wavevector (kx=2.35 μm). (e–h) The pumping power is constant (80 μW), while the in-plane momentum varies. The secondary spot appearing in front of the main signal at ~10 ps is a reflection from the substrate edge. Their spot separation increases with the angle of injection (that is, with k). Such reflection does not affect the main packet, especially in the case of the k used for the optimized X-wave (separation ~two times the spot width).
The role played by the in-plane momentum kx is shown in Figure 3e–3h, where only the injection angle is changed, while keeping the initial density constant. In Figure 3e, despite the large nonlinearities that are as high as in Figure 3d, no redistribution is observed. Upon gradually increasing the injection angle, shown in Figure 3f and 3g, the packet shows again a marked anisotropy in its diffusion along the longitudinal and transverse directions. This is due to the larger difference between the longitudinal and transverse effective masses in the excited region of the dispersion. This difference reaches its maximum at 2.35 μm−1, where the reshaping is optimized, Figure 3h.
Localization and superluminality
We now focus on the propagation of the polariton XWs. Figure 4a shows the time evolution of the normalized polariton population (blue points) together with the pump pulse temporal envelope (solid red curve). The t=0 ps has been chosen to be at the maximum of the polariton population, which is when the pulse has essentially finished its pumping action and the polaritons free evolution starts. The growing longitudinal/transverse anisotropy can be appreciated upon a visual comparison between the associated amplitude time space charts in Figure 4b (longitudinal) and Figure 4d (transverse), as well as from the associated phase charts in Figure 4c and 4e. In the longitudinal charts, the signal propagates for 40 μm with a constant speed of ~1.20 μm ps−1, and a final width very similar to the original shape. However, in the transverse maps, the width reveals the standard wave packet diffusion. This is clearly confirmed in Figure 4g and 4h, where both the longitudinal and transverse profiles are reported to be t=0 and t=30 ps, respectively, together with their associated Gaussian fits.
Time space profiles of the X-wave. (a) Blue shows the time evolution of the normalized total polariton population and red shows the temporal envelope of the pump pulse. (b–e) Vertical (b and c) and horizontal (d and e) time space charts of the amplitude and phase. The dashed white lines in b and d represent the temporal evolution of the FWHM of the packet density. In c, the longitudinal phase is shown with respect to the moving reference frame. Moreover, in both c and e, the phase is constant in the center of the main packet. The circled arrows in c represent two phase singularities in the time space domain. In d and e, the transverse crosscuts are taken at a longitudinal position, which follows the packet maximum. (f and g) are the longitudinal and transverse normalized density profiles at t=0 ps (f) and t=30 ps (g), and solid lines indicate Gaussian fits. The dynamics are relative to P=75 μW and kx=2.35 μm−1 (as in Figure 3d).
The power dependence of the differential spreading along the two directions is analyzed in detail in Figure 5a. Here, the temporal evolution of the longitudinal and transverse FWHM densities is shown for different excitation powers, corresponding to the previous Figure 3a–3d. For the lowest power (P=22 μW, red line), the reshaping is completely absent, and the wave packet expands continuously in both directions. The longitudinal (filled dots) and transverse (open dots) spreading have the same spreading rate. At larger injected power, and consequently stronger nonlinearity, the degree of anisotropy between the longitudinal and transverse size gradually increases (P=45 μW and P=53 μW are indicated by the orange and green dots, respectively), leading to the suppression of the longitudinal spread. Strikingly, for P=75 μW, the packet undergoes a longitudinal squeezing during the first 10 ps. This is associated with the nonlinear redistribution into the X-wave packet, whose shape can be neatly distinguished in the previous maps of Figure 3d. Based on these features, we may state that it is possible to qualitatively distinguish between the three main dynamic phases: pulse injection (−5÷0 ps), initial redistribution (0÷10 ps) and propagation (10÷30 ps). The numerical simulations of Figure 5b reproduce the experiments in a perfect agreement with our trends. We again note that this phenomenology is different from the bright solitons that are sustained under a cw background pump beam as in Refs 41, 42. In that case, the pump keeps the background just below the bistability threshold over its width and feeds the nonlinear maintenance of the moving soliton, which can propagate only within the pump spot. Instead, here, while the transverse width is not conserved (in agreement with the lateral positive mass), the longitudinal width is preserved along the propagation length of more than 40 μm, despite the packet arriving to this position with only a very small fraction of the initial population and density (one order of magnitude lower). Furthermore, the bright solitons in Refs 41, 42 exhibit a propagation speed that is set uniquely by the injection k of the cw background pump and, being dissipative solitons, is not affected by the seed pulse. In contrast, the X-wave offers the possibility to tune the group velocity of the packet using the incident in-plane momentum, and can furthermore achieve a fine degree of tunability of the peak speed using the power control of the exciting pulse.
Wave packet spreading and speeds. (a) Experimental longitudinal (solid line) and transverse (dashed line) density FWHMs with respect to time at four different excitation powers for kx=2.35 μm−1. (b) Simulation of the time evolution of the longitudinal (solid line) and transverse (dashed line) density FWHMs, for different initial total populations and a kx=2.55 μm−1 in-plane momentum. The arrows on the right side in both panels indicate the difference between the longitudinal and transverse widths. (c) Experimental velocities of the center-of-mass (blue dots) and peak (orange dots) positions at four different excitation powers (at kx=2.35 μm−1). (d) Simulated velocities of the center-of-mass (blue dots) and peak (orange dots) positions at four excitation powers (at kx=2.55 μm−1). The arrows on the right side in both panels indicate the percentage difference between the peak and center-of-mass speeds at the largest power. The horizontal dashed lines represent the average of the center-of-mass velocities. The different values between the experimental and computational results are due to the different kx used and to an imperfect calibration of the simulation parameters.
Indeed, our wave packet exhibits one of the most interesting signatures of Bessel X-pulses, superluminality. This effect is driven by the Bessel cone angle θ associated with the X-pulses48, 49, 50, 51, whose peak moves (in vacuum) at v=c/cos(θ). In any system, the role of c is played by the group velocity vg as obtained from the specific dispersion slope (illustrated for polariton waves in Figure 1). Here, we experimentally observe an increase in the speed of the density peak with respect to the center-of-mass speed, up to a value of 6% in the case of the largest power, as shown in Figure 5c. We can evaluate that a maximum angle θ~18° is reached for P=75 μW. In terms of transverse in-plane momentum, this angle corresponds to a δky~±0.6 μm−1. These lateral k-states are induced in the initial FWM along the (nearly flat) transverse direction of the dispersion. Numerical simulations performed at different initial populations confirm the trend of the increase in the peak velocity with respect to the center-of-mass, as shown in Figure 5d. We stress that different degrees of superluminal speed could be achieved without changing any other parameter (for example, spot width in real/k-space, central momentum, central energy, pulse width) but only the pulse power, consequently tuning the strength of the nonlinearity.
A complementary nonlinear effect is obtained along the longitudinal direction. As introduced in Figure 2, a specific feature of our structured polariton XW is represented by the leading and trailing islands that are developed around the main packet during the initial reshaping. These features can be neatly resolved due to the strong coherence properties of polaritons. Indeed, such coherence is maintained during the interference phenomena between the nonlinearly induced counter-propagating flows. In particular, the faster vg(kx) leading and the slower vg(kx) trailing subpackets represent the FWM states that are initially created at smaller (kx−δkx) and larger (kx+δkx) longitudinal momentum, respectively. The counter intuitive association between the group velocity and momentum differentials are due to the negative curvature of the dispersion. Instead, the circular shape of the interference between the three packets suggests that the two excited FWM states have a larger transverse extension in momentum space (ky) with respect to the primary transverse profile. In Figure 6a, we report both the amplitude and phase longitudinal profiles (corresponding to P=75 μW and t=7.5 ps) to highlight the presence of two sharp π-jumps in front and behind of the main packet, which is in a perfect spatial correspondence to dark dips in the density profile. The ignition time of such π-jumps is also visible in the time space charts of Figure 4c at t≈7.5–8.0 ps. This is also the time of the vortex–antivortex pair generation in real space (see the main sequence in Figure 2). It is interesting to note that the appearance of such dark lines themselves is like a couple of phase singularities (quantum vortex) in the time space domain of Figure 4c. In general, the nonlinear self-development of a π-jump may be a signature of a dark soliton37, 52, which can be sustained in 2D condensates by repulsive interactions53. In Figure 6b, we report the evolution of the phase profiles at equidistant time frames (every 2.5 ps). The profiles indicate how the sharp π-jump is only present in a given frame at early times, before being smoothed as expected, due to a loss in the intensity. Hence, we may conclude that the dark soliton is a transient structure, a result of the nonlinear way we ignite the XW in the polariton fluid. The dark soliton is then washed out, without representing an intrinsic feature of the XW itself, as opposed to the longitudinal localization, which is instead preserved in time.
Transient dark soliton. (a) Phase (solid orange line) and amplitude (blue dots) central crosscut profiles along the propagation direction at t=7.5 ps and for P=75 μW. (b) Phase profiles along the longitudinal axis at fixed time intervals of 2.5 ps. The top line represents t=0 ps, while the subsequent profiles are mutually shifted down the same amount for clarity. The phase profiles are shown with respect to the moving frame of reference, and the phase is forced to be constant at the edge of the packet.
Conclusions
We have experimentally demonstrated the possibility to excite a peculiar class of traveling localized wave packets, called X-waves, in 2D exciton-polariton fluids. Self-generation of an X-wave out of a Gaussian excitation spot is obtained via a weakly nonlinear asymmetric process with respect to two directions of the nonparabolic polariton dispersion. The dynamics of the packet are observed using ultrafast imaging, revealing a propagation over tens of micrometers, only limited by the polariton dissipation. We have tuned the nonlinearity and the injected in-plane momentum to achieve both the optimal effect and preserve the longitudinal localization, even when the density fades away. Different degrees of superluminality have been achieved and associated with the variable transverse angular aperture induced by the nonlinear process in its early stage. Polariton-based all-optical platforms are devised as robust candidates to study the fundamental science connected to 2D X-wave packets and possible future applications exploiting them in signal propagation.
Alternative 2D platforms are represented by, for example, multilayer stacks supporting Bloch surface waves (BSWs) at the external interface. These surface modes naturally exhibit very large in-plane speed, which converts into long-range propagation, with negative mass dispersion and have exhibited exploitable nonlinearity upon coupling with an organic layer that is stable up to room temperature54. The BSWs are enabling competitive systems compared to surface plasmon resonance for label-free high-sensitivity biosensing55. Such systems also offer the possibility to easily pattern the external open surface to realize planar guiding or focusing elements56, or even tilted, top-grating, launching, diffraction-free surface waves57, analogous to what has been previously realized with plasmonic systems58. Hence, BSW polaritons are a natural evolution for the study of X-wave pulse propagation over hundreds of μm and their exploitation for novel 2D optical tweezers and sensing combined functionalities.
Both QW-MC and BSW polariton platforms represent nanophotonic technologies that are characterized by a strong and tunable χ(3) nonlinearity resulting from polariton-polariton interactions. The third-order nonlinearity governs not only the FWM process but also other useful phenomena, such as self- and cross-Kerr modulation. Thus, we expect that they will be highly pronounced in our polariton superfluid. Tunable, efficient, nonlinear interactions are a ‘holy grail’ in photonic and optical systems59, 60 and quantum computing61 for building the optical gates necessary to construct a quantum computer.
Author contributions
LD and MM proposed the experiments. AG, LD, DB, MDG, GG and DS set up the laboratory configurations. AG and LD performed the experiments and analyzed the data. OV, MM and MS developed the theory, performed numerical simulations and provided the theoretical interpretations. All the authors discussed the results. AG, LD, OV, MM, MS and DS wrote the manuscript. DS supervised the research.
References
Recami E, Zamboni-Rached M, Hernandez-Figueroa HE . Localized waves: a scientific and historical introduction. In: Hernández-Figueroa HE, Zamboni-Rached M, Recami E, editors. Localized Waves, Wiley Series in Microwave and Optical Engineering. Hoboken, N.J.: Wiley-Interscience; 2008.
Recami E, Zamboni-Rached M . Localized waves: a review. In: Hawkes P, editor. Advances in Imaging and Electron Physics, Vol. 156. Amsterdam: Elsevier; 2009. p235–353.
Sõnajalg H, Rätsep M, Saari P . Demonstration of the Bessel-X pulse propagating with strong lateral and longitudinal localization in a dispersive medium. Opt Lett 1997; 22: 310–312.
Durnin J, Miceli Jr JJ, Eberly JH . Diffraction-free beams. Phys Rev Lett 1987; 58: 1499–1501.
Salo J, Fagerholm J, Friberg AT, Salomaa MM . Unified description of nondiffracting X and Y waves. Phys Rev E 2000; 62: 4261–4275.
Lu JY, Greenleaf JF . Ultrasonic nondiffracting transducer for medical imaging. IEEE Trans Ultrason Ferroelect Freq Control 1990; 37: 438–447.
Lu JY, Greenleaf JF . Nondiffracting X waves-exact solutions to free-space scalar wave equation and their finite aperture realizations. IEEE Trans Ultrason Ferroelect Freq Control 1992; 39: 19–31.
Yalizay B, Ersoy T, Soylu B, Akturk S . Fabrication of nanometer-size structures in metal thin films using femtosecond laser Bessel beams. Appl Phys Lett 2012; 100: 031104.
Zamboni-Rached M, Recami E, Hernández-Figueroa H . New localized superluminal solutions to the wave equations with finite total energies and arbitrary frequencies. Eur Phys J D 2002; 21: 217–228.
Zamboni-Rached M, Fontana F, Recami E . Superluminal localized solutions to Maxwell equations propagating along a waveguide: the finite-energy case. Phys Rev E 2003; 67: 036620.
Conti C, Trillo S . Nonspreading wave packets in three dimensions formed by an ultracold bose gas in an optical lattice. Phys Rev Lett 2004; 92: 120404.
Voronych O, Buraczewski A, Matuszewski M, Stobiñska M . Exciton-polariton localized wave packets in a microcavity. Phys Rev B 2016; 93: 245310.
Efremidis NK, Siviloglou GA, Christodoulides DN . Exact X-wave solutions of the hyperbolic nonlinear Schrödinger equation with a supporting potential. Phys Lett A 2009; 373: 4073–4076.
Conti C . Generation and nonlinear dynamics of X waves of the Schrödinger equation. Phys Rev E 2004; 70: 046613.
Sedov ES, Iorsh IV, Arakelian SM, Alodjants AP, Kavokin A . Hyperbolic metamaterials with bragg polaritons. Phys Rev Lett 2015; 114: 237402.
Couairon A, Gaižauskas E, Faccio D, Dubietis A, Di Trapani P . Nonlinear X-wave formation by femtosecond filamentation in Kerr-media. Phys Rev E 2006; 73: 016608.
Kolesik M, Wright EM, Moloney JV . Dynamic nonlinear X waves for femtosecond pulse propagation in water. Phys Rev Lett 2004; 92: 253901.
Conti C, Trillo S, Di Trapani P, Valiulis G, Piskarskas A et al. Nonlinear electromagnetic X waves. Phys Rev Lett 2003; 90: 170406.
Di Trapani P, Valiulis G, Piskarskas A, Jedrkiewicz O, Trull J et al. Spontaneously generated X-shaped light bullets. Phys Rev Lett 2003; 91: 093904.
Ciattoni A, Conti C . Quantum electromagnetic X waves. J Opt Soc Am B 2007; 24: 2195–2198.
Sanvitto D, Kéna-Cohen S . The road towards polaritonic devices. Nat Mater 2016; 15: 1061–1073.
Byrnes T, Kim NY, Yamamoto Y . Exciton-polariton condensates. Nat Phys 2014; 10: 803–813.
Dagvadorj G, Fellows JM, Matyjaśkiewicz S, Marchetti FM, Carusotto I et al. Nonequilibrium phase transition in a two-dimensional driven open quantum system. Phys Rev X 2015; 5: 041028.
Deng H, Haug H, Yamamoto Y . Exciton-polariton Bose-Einstein condensation. Rev Mod Phys 2010; 82: 1489–1537.
Amo A, Sanvitto D, Laussy FP, Ballarini D, del Valle E et al. Collective fluid dynamics of a polariton condensate in a semiconductor microcavity. Nature 2009; 457: 291–295.
Kasprzak J, Richard M, Kundermann S, Baas A, Jeambrun P et al. Bose-Einstein condensation of exciton polaritons. Nature 2006; 443: 409–414.
Balili R, Hartwell V, Snoke D, Pfeiffer L, West K . Bose-Einstein condensation of microcavity polaritons in a trap. Science 2007; 316: 1007–1010.
Kavokin AV, Baumberg JJ, Malpuech G, Laussy FP . Microcavities, 2 edn. Oxford, New York: Oxford University Press; 2017.
Colas D, Laussy FP . Self-interfering wave packets. Phys Rev Lett 2016; 116: 026401.
Walker PM, Tinkler L, Skryabin DV, Yulin A, Royall B et al. Ultra-low-power hybrid light-matter solitons. Nat Commun 2015; 6: 8317.
Vladimirova M, Cronenberger S, Scalbert D, Kavokin KV, Miard A et al. Polariton-polariton interaction constants in microcavities. Phys Rev B 2010; 82: 075301.
Amo A, Lefrère J, Pigeon S, Adrados C, Ciuti C et al. Superfluidity of polaritons in semiconductor microcavities. Nat Phys 2009; 5: 805–810.
Berceanu AC, Dominici L, Carusotto I, Ballarini D, Cancellieri E et al. Multicomponent polariton superfluidity in the optical parametric oscillator regime. Phys Rev B 2015; 92: 035307.
Amo A, Pigeon S, Sanvitto D, Sala VG, Hivet R et al. Polariton superfluids reveal quantum hydrodynamic solitons. Science 2011; 332: 1167–1170.
Sanvitto D, Marchetti FM, Szymańsk MH, Tosi G, Baudisch M et al. Persistent currents and quantized vortices in a polariton superfluid. Nat Phys 2010; 6: 527–533.
Whittaker CE, Dzurnak B, Egorov OA, Buonaiuto G, Walker PM et al Polariton pattern formation and its statistical properties in a semiconductor microcavity. Preprint at: arXiv:161203048, 2016.
Dominici L, Petrov M, Matuszewski M, Ballarini D, De Giorgi M et al. Real-space collapse of a polariton condensate. Nat Commun 2015; 6: 8993.
Manni F, Lagoudakis KG, Liew TCH, André R, Deveaud-Plédran B . Spontaneous pattern formation in a polariton condensate. Phys Rev Lett 2011; 107: 106401.
Wertz E, Ferrier L, Solnyshkov DD, Johne R, Sanvitto D et al. Spontaneous formation and optical manipulation of extended polariton condensates. Nat Phys 2010; 6: 860–864.
Ostrovskaya EA, Abdullaev J, Desyatnikov AS, Fraser MD, Kivshar YS . Dissipative solitons and vortices in polariton Bose-Einstein condensates. Phys Rev A 2012; 86: 013636.
Sich M, Krizhanovskii DN, Skolnick MS, Gorbach AV, Hartley R et al. Observation of bright polariton solitons in a semiconductor microcavity. Nat Photonics 2012; 6: 50–55.
Egorov OA, Gorbach AV, Lederer F, Skryabin DV . Two-dimensional localization of exciton polaritons in microcavities. Phys Rev Lett 2010; 105: 073903.
Ballarini D, De Giorgi M, Cancellieri E, Houdré R, Giacobino E et al. All-optical polariton transistor. Nat Commun 2013; 4: 1778.
Sun C, Wade MT, Lee Y, Orcutt JS, Alloatti L et al. Single-chip microprocessor that communicates directly using light. Nature 2015; 528: 534–538.
Colas D, Dominici L, Donati S, Pervishko AA, Liew TC et al. Polarization shaping of Poincaré beams by polariton oscillations. Light Sci Appl 2015; 4: e350, doi:10.1038/lsa.2015.123.
Dominici L, Colas D, Donati S, Cuartas JPR, De Giorgi M et al. Ultrafast control and Rabi oscillations of polaritons. Phys Rev Lett 2014; 113: 226401.
Voronych O, Buraczewski A, Matuszewski M, Stobińska M . Numerical modeling of exciton-polariton Bose-Einstein condensate in a microcavity. Comput Phys Commun 2017; 215: 246–258.
Bonaretti F, Faccio D, Clerici M, Biegert J, Di Trapani P . Spatiotemporal amplitude and phase retrieval of Bessel-X pulses using a Hartmann-Shack Sensor. Opt Express 2009; 17: 9804–9809.
Mugnai D, Ranfagni A, Ruggeri R . Observation of superluminal behaviors in wave propagation. Phys Rev Lett 2000; 84: 4830–4833.
Bowlan P, Valtna-Lukner H, Lôhmus M, Piksarv P, Saari P et al. Measuring the spatiotemporal field of ultrashort Bessel-X pulses. Opt Lett 2009; 34: 2276–2278.
Valtna-Lukner H, Bowlan P, Lôhmus M, Piksarv P, Trebino R et al. Direct spatiotemporal measurements of accelerating ultrashort Bessel-type light bullets. Opt Express 2009; 17: 14948–14955.
Dominici L, Dagvadorj G, Fellows JM, Ballarini D, De Giorgi M et al. Vortex and half-vortex dynamics in a nonlinear spinor quantum fluid. Sci Adv 2015; 1: e1500807.
Rodrigues AS, Kevrekidis PG, Carretero-González R, Cuevas-Maraver J, Frantzeskakis DJ et al. From nodeless clouds and vortices to gray ring solitons and symmetry-broken states in two-dimensional polariton condensates. J Phys Condens Matter 2014; 26: 155801.
Lerario G, Ballarini D, Fieramosca A, Cannavale A, Genco A et al. High-speed flow of interacting organic polaritons. Light Sci Appl 2017; 6: e16212, doi:10.1038/lsa.2016.212.
Sinibaldi A, Danz N, Descrovi E, Munzert P, Schulz U et al. Direct comparison of the performance of Bloch surface wave and surface plasmon polariton sensors. Sens Actuators B Chem 2012; 174: 292–298.
Yu LB, Barakat E, Sfez T, Hvozdara L, Di Francesco J et al. Manipulating Bloch surface waves in 2D: a platform concept-based flat lens. Light Sci Appl 2014; 3: e124, doi:10.1038/lsa.2014.5.
Wang RX, Wang Y, Zhang DG, Si GY, Zhu LF et al. Diffraction-free Bloch surface waves. ACS Nano 2017; 11: 5383–5390.
Lin J, Dellinger J, Genevet P, Cluzel B, de Fornel F et al. Cosine-gauss plasmon beam: a localized long-range nondiffracting surface wave. Phys Rev Lett 2012; 109: 093904.
Kishida H, Matsuzaki H, Okamoto H, Manabe T, Yamashita M et al. Gigantic optical nonlinearity in one-dimensional Mott-Hubbard insulators. Nature 2000; 405: 929–932.
Deng L, Hagley EW, Wen J, Trippenbach M, Band Y et al. Four-wave mixing with matter waves. Nature 1999; 398: 218–220.
Gottesman D . The Heisenberg representation of quantum computers. Preprint at: arXiv:quant-ph/9807006, 1998.
Acknowledgements
We thank R Houdré and A Bramati for the microcavity device. AG, LD, DB, MDG, GG and DS are supported by the European Research Council POLAFLOW Grant 308136 and the Italian MIUR project Beyond Nano. MS and OV are supported by the NCN Grant no. 2012/04/M/ST2/00789 and MNiSW Iuventus Plus project no. IP 2014 044873. MS acknowledges support from the FNP project FIRST TEAM/2016-2/17. MM acknowledges support from NCN Grant 2015/17/B/ST3/02273.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications’website .
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Gianfrate, A., Dominici, L., Voronych, O. et al. Superluminal X-waves in a polariton quantum fluid. Light Sci Appl 7, 17119 (2018). https://doi.org/10.1038/lsa.2017.119
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2017.119