Abstract
Metamaterials based on effective media can be used to produce a number of unusual physical properties (for example, negative refraction and invisibility cloaking) because they can be tailored with effective medium parameters that do not occur in nature. Recently, the use of coding metamaterials has been suggested for the control of electromagnetic waves through the design of coding sequences using digital elements ‘0’ and ‘1,' which possess opposite phase responses. Here we propose the concept of an anisotropic coding metamaterial in which the coding behaviors in different directions are dependent on the polarization status of the electromagnetic waves. We experimentally demonstrate an ultrathin and flexible polarization-controlled anisotropic coding metasurface that functions in the terahertz regime using specially designed coding elements. By encoding the elements with elaborately designed coding sequences (both 1-bit and 2-bit sequences), the x- and y-polarized waves can be anomalously reflected or independently diffused in three dimensions. The simulated far-field scattering patterns and near-field distributions are presented to illustrate the dual-functional performance of the encoded metasurface, and the results are consistent with the measured results. We further demonstrate the ability of the anisotropic coding metasurfaces to generate a beam splitter and realize simultaneous anomalous reflections and polarization conversions, thus providing powerful control of differently polarized electromagnetic waves. The proposed method enables versatile beam behaviors under orthogonal polarizations using a single metasurface and has the potential for use in the development of interesting terahertz devices.
Similar content being viewed by others
Introduction
Artificial metamaterials composed of subwavelength structures can be described by effective media with continuous medium parameters1, 2, 3, and because the effective permittivity and/or permeability can be tailored to reach values beyond what is possible in nature, such metamaterials have powerful abilities to manipulate electromagnetic waves. A number of new physical properties have been observed, such as negative refraction4, 5, perfect imaging6 and invisible cloaking7, 8, 9, 10. In addition to the extreme medium parameters required by these new physics, gradient refractive indexes have also been realized by drilling air holes or printing metallic elements on dielectric substrates, which have been used to produce various functional devices11, 12, 13, 14. However, these approaches rely on the accumulation of phase delays during wave propagation, which are always associated with large thicknesses and pose great challenges for fabrications at terahertz frequencies. Therefore, reducing the thickness of a bulk metamaterial to that of a surface, which is called a metasurface, will be highly useful because these thinner metamaterials require less physical space and can be bent and twisted as desired15.
To overcome the abovementioned limitations, the generalized Snell’s laws of reflection and refraction were proposed by introducing abrupt phase changes on an ultrathin metasurface16, 17. A metasurface consisting of an array of C-shaped antennas has been presented to control both the phase and amplitude profiles of the transmitted waves18, which can be utilized to design complex terahertz devices, such as dual-polarity plasmonic metalens19 and holograms20, 21, 22. Other approaches, such as a Y-shaped nano-antenna23, complementary structure of a V-shaped antenna24 and graphene-loaded plasmonic antenna25, have been suggested for metasurfaces to offer more freedom in designing the desired wavefronts. Because of the low loss, ultrathin thickness and conformal capability, metasurfaces have shown considerable potential for use in a wide range of applications, including those that require microwave26, 27, 28, terahertz29, 30, infrared31 and visible19, 32, 33 frequencies.
In addition to effective medium parameters, digital metamaterial has recently been proposed as an alternative approach to describing metamaterials that use the binary codes ‘0’ and ‘1’, which denote the discretized reflection phases of only two elemental materials34. Two reflection-type unit cells designed with a 180° phase difference35 can be used to implement digital metamaterials and programmable metamaterials by pre-designing or digitally controlling the distribution of the ‘0’ and ‘1’ coding particles on a two-dimensional (2D) surface. Based on this concept, various functionalities, such as steering, bending, focusing and random electromagnetic wave scattering, can be simply implemented by digitally encoding the metasurfaces with the corresponding coding sequences. Recently, this idea has been extended to terahertz frequencies and the manipulation of terahertz waves by designing the coding particles using Minkowski fractal elements36. Flexible and conformal coding metamaterials have also been proposed at terahertz frequencies to mimic the diffusion reflections of a rough surface37. In the aforementioned coding schemes, however, the coding behavior is independent of the polarization status of the electromagnetic waves because of the isotropic geometry of the unit cells35, 36, 37; hence, they are isotropic coding metamaterials.
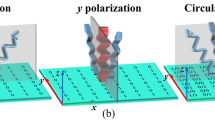
Here we propose the concept of an anisotropic coding metamaterial that has distinct coding behavior for different polarizations and demonstrate the first polarization-controlled coding metasurface, which is sketched in Figure 1a and 1b. In this specific illustration, under the normal (−z direction) incidence of terahertz waves, an anomalous reflection17 occurs to the right side when the incident field is x-polarized (Figure 1a), whereas an anomalous reflection occurs to the left side when the incident field is y-polarized (Figure 1b). The polarization control through anisotropic coding is flexible and independent, and distinct functionalities can be realized via different polarizations. We present two types of unit cells, a square-shaped and a dumbbell-shaped metallic structure, as the coding elements for the anisotropic coding metamaterials, and they can independently reflect the normally incident terahertz waves with either 0° (state ‘0’) or 180° (state ‘1’) reflection phases under two orthogonal polarizations. The same unit cells are then utilized to build up a 2-bit anisotropic coding metasurface in which the four different digital states ‘00’ (0°), ‘01’ (90°), ‘10’ (180°) and ‘11’ (270°) are independently implemented under different polarizations. We note that the absolute phase values for each of these digital states do not affect the performance of the coding metamaterials and therefore have been normalized to the reflection phase of the digital state ‘0’ (or ‘00’ for the 2-bit case) for simplicity. The far-field scattering patterns and near-electric-field distributions are presented to demonstrate the polarization-controlled dual-functional characteristics of the encoded metasurface, and any of the dual functions supported by the anisotropic coding metasurface (such as anomalous reflection and random diffusion of terahertz waves) are realized by switching the polarization state of the incident wave between the x and y directions. Two different terahertz time-domain spectroscopy (THz-TDS) systems are employed to experimentally verify the anomalous deflections and random scattering.
Illustration of the anisotropic coding metamaterial and the structure design. (a and b) An example to demonstrate the flexibility of the encoded metasurface, which can anomalously reflect the normal incident beam to the right side under x polarization and the left side under y polarization. (c) The structure of anisotropic coding element ‘1/0’ (without the metallic background). (d) Reflection phases and the corresponding phase difference for the anisotropic unit cell ‘1/0’ under x and y polarizations. (e) The structure of the 16 unit cells for the 2-bit anisotropic coding metasurface.
Materials and methods
1-bit anisotropic coding metamaterials
We start with the 1-bit case to demonstrate the control of functionalities via the polarization of the anisotropic coding metasurface. An elaborately designed dumbbell-shaped metallic structure is presented as the unit cell of the anisotropic coding metasurface as illustrated in Figure 1c, which shows two different coding states, ‘1’ and ‘0,' under the normal incidences of x- and y-polarized electromagnetic waves. Because of the anisotropy of the geometry, the reflection coefficient of an anisotropic coding particle is expressed by a tensor  as follows:
as follows:

where  and
and  represent the reflection coefficients of a certain coding particle (m,n) on the coding metasurface under the x and y polarizations, respectively. When
represent the reflection coefficients of a certain coding particle (m,n) on the coding metasurface under the x and y polarizations, respectively. When  , the anisotropic coding metasurface is reduced to isotropic.
, the anisotropic coding metasurface is reduced to isotropic.
Four parameters are used to characterize the geometry of the dumbbell-shaped structure: heights h1 and h2 and widths w1 and w2. The structure is printed on a polyimide dielectric substrate with an opaque metallic ground to provide for total reflections. We show that arbitrarily reflected phases can be independently obtained under x and y polarizations by controlling these four parameters. A dielectric constant ɛ=3.0 and loss tangent δ=0.03 are set in the simulations for the selected polyimide. Gold with a thickness of 200 nm is chosen for the metallic layer. Because the plasma frequency of gold is far beyond the terahertz frequency, it is safe to treat the gold as a perfectly electric conductor at the terahertz frequency (with conductivity of 4.56 × 107 S m−1). Other geometrical parameters designed to operate at ~1 THz for the 1-bit anisotropic coding element are as follows: h1=45 μm, h2=20 μm, w1=37.5 μm and w2=18.5 μm. The numerical simulation results of the reflected phases (Figure 1d) obtained by the commercial software program CST Microwave Studio (Computer Simulation Technology AG, Framingham, MA, USA) indicate that the anisotropic unit cell (Figure 1c) provides opposite coding states with ~180° phase differences in a wide frequency band (an exact 180° phase difference at 1 THz) under the normal incidences of terahertz waves, with state ‘1’ provided for x polarizations and state ‘0’ provided with y polarizations. Hence, we refer to the anisotropic unit cell as a ‘1/0’ coding particle, and the binary codes before and after the slash symbol (/) represent the digital states under x and y polarizations, respectively. Similarly, when the anisotropic unit cell is rotated by 90° along the z axis, it will produce ‘0’ and ‘1’ coding states for the x- and y-polarized incident terahertz waves (Supplementary Fig. S1a), resulting in the ‘0/1’ coding particle. Detailed simulation configurations for the reflection coefficients are provided in the Supplementary Information.
To flexibly control the 1-bit coding states by polarization, we still require ‘0/0’ and ‘1/1’ coding particles, which can be easily implemented by the isotropic unit cells35, 36. Here we selected the metallic square structure (Supplementary Fig. S1c)35 with length a printed on the polyimide substrate with a period p=50 μm and thickness d=20 μm. When a=45 μm, the structure provides the ‘0/0’ coding state for both polarizations, and when a=30 μm, the structure provides the ‘1/1’ coding state (Supplementary Fig. S1d). The square can be considered a degenerated form of the dumbbell-shaped structure with w1=w2 and h1=w1=a. Hence, we conclude that the reflection phases of the x- and y-polarized waves can be controlled independently by altering the four geometrical parameters (h1, h2, w1 and w2). By arranging the four coding particles (‘0/0’, ‘0/1’, ‘1/0’ and ‘1/1’) with certain coding sequences, arbitrary functionalities can be independently realized in either polarization.
For a quantitative illustration of the anisotropic coding metamaterials, we first encode a metasurface with a coding sequence of ‘010101…’ under both x and y polarizations, which is formed by repeating a 2D coding matrix:

We adopt a so-called ‘super unit cell,’ which is generated by a subarray of the same basic unit cells with size N × N, to minimize the unwanted coupling effect resulting from adjacent units with different geometries. A smaller super unit cell is preferred because of the minimum reflected angle allowed in our measurement system. Here the size of the super unit cell is 4 × 4. The deflected angle (that is, the anomalous reflection angle) can then be calculated as θ=sin−1(λ/Γ)=48.5°, where λ and Γ represent the free-space wavelength (300 μm at 1 THz) and physical length of one period of the gradient phase distribution (400 μm), respectively. The Supplementary Information includes descriptions of the derivations of the anomalous reflection angle. A final encoded metasurface board that includes 16 × 16 super unit cells (Figure 2a) is built up for the numerical simulations. Figure 3a and 3b shows the three-dimensional (3D) far-field scattering patterns of the anisotropic coding metasurface under the normal incidences with x and y polarizations at 1 THz. Here the entire encoded metasurface is simulated using the open boundary condition and plane wave excitation in CST Microwave Studio. The Supplementary Information includes detailed descriptions of the simulation setup for the far-field scattering pattern. The main lobe clearly deviates from the z axis to 48° in the y–z plane for the x-polarized terahertz waves and in the x–z plane for the y-polarized terahertz waves. The deviation angle is consistent with the analytical predictions. The bistatic scattering curves in the y–z and x–z planes for the x and y polarizations are exactly the same (presented in Supplementary Fig. S3a). To interpret the physical insights, we also produce the scattered electric field distributions Ex and Ey under the x and y polarizations, respectively, on the y–z and x–z cutting planes in the near-field region, which are illustrated in Supplementary Fig. S3b and S3c, respectively. We note that most of the electromagnetic energy is deflected to two symmetrically oriented directions in planes orthogonal to the polarization directions. We attribute the slight disturbance observed in the scattered electric field to the real reflection phases with adjacent super unit cell coupling, which are not exactly 0° and 180° at 1 THz. However, this effect can be suppressed if we increase the size of the super unit cell.
Coding patterns of the 1-bit and 2-bit coding metasurfaces and their zoomed views. (a) Pattern with coding matrix  that contains 16 × 16 super unit cells with a size of 4 × 4. (b) Pattern with coding matrix
that contains 16 × 16 super unit cells with a size of 4 × 4. (b) Pattern with coding matrix  that contains 16 × 16 super unit cells with a size of 4 × 4. (c) Pattern with coding matrix
that contains 16 × 16 super unit cells with a size of 4 × 4. (c) Pattern with coding matrix  that contains 32 × 32 super unit cells with a size of 2 × 2. (d) Pattern with coding matrix
that contains 32 × 32 super unit cells with a size of 2 × 2. (d) Pattern with coding matrix  that contains 16 × 16 super unit cells with a size of 3 × 3. (e) Pattern with coding matrix
that contains 16 × 16 super unit cells with a size of 3 × 3. (e) Pattern with coding matrix  that contains 32 × 32 super unit cells with a size of 2 × 2. (f) Pattern with coding matrix
that contains 32 × 32 super unit cells with a size of 2 × 2. (f) Pattern with coding matrix  that contains 32 × 32 super unit cells with a size of 2 × 2.
that contains 32 × 32 super unit cells with a size of 2 × 2.
Simulated 3D and 2D scattering patterns for the 1-bit anisotropic coding metasurface. (a–c) 3D far-field scattering patterns of the metasurface encoded with coding matrix  under the x polarization, y polarization and 45° (with respect to the x axis) polarization, respectively. (d) Near-electric-field distributions for the same metasurface in a. The electric fields on the y–z and x–z cutting planes are plotted with components Ex and Ey, respectively. (e and f) 3D far-field scattering patterns of the metasurface encoded with coding matrix
under the x polarization, y polarization and 45° (with respect to the x axis) polarization, respectively. (d) Near-electric-field distributions for the same metasurface in a. The electric fields on the y–z and x–z cutting planes are plotted with components Ex and Ey, respectively. (e and f) 3D far-field scattering patterns of the metasurface encoded with coding matrix  under x and y polarizations, respectively. (g) 2D far-field scattering pattern plotted in the y–z plane for the same metasurface in e under x-polarized illumination. (h) Scattering gain, which is defined by the reduction of backscattering compared with the bare metallic case, for the same metasurface as in e under y polarization.
under x and y polarizations, respectively. (g) 2D far-field scattering pattern plotted in the y–z plane for the same metasurface in e under x-polarized illumination. (h) Scattering gain, which is defined by the reduction of backscattering compared with the bare metallic case, for the same metasurface as in e under y polarization.
When the incident terahertz beam is polarized by a 45° angle with respect to the x axis, it will be equally split into four symmetrically oriented beams at the same angle with respect to the z axis as shown in Figure 3c. This phenomenon is further verified by the near-field distributions depicted in Figure 3d, in which Ex and Ey are plotted in the y–z and x–z cutting planes, respectively. Hence, we conclude that the intensities of these four deflected beams can be arbitrarily controlled by adjusting the polarization direction of the incident electric field, and this functionality could be exploited in a number of interesting applications, such as terahertz beam splitters.
The 1-bit anisotropic coding metamaterial can also be designed to deflect the x-polarized terahertz beam to two symmetrical directions using coding sequence 010101… and randomly redirect the y-polarized beam to all directions (that is, diffusions) using an optimized ‘0’ and ‘1’ coding sequence (Figure 2b). In this case, the 3D far-field scattering patterns under the x and y polarizations are shown in Figure 3e and 3f, respectively. Although the coding pattern is different from that shown in Figure 2a, the incident beam is still deflected as two equal beams pointing to the angle θ=±48° with respect to the z axis in the y–z plane under the x polarization (Figure 3g). However, for the y polarization, numerous small lobes pointing in different directions are observed in Figure 3f, indicating that the terahertz scattering of a metallic plate can be significantly reduced by covering these encoded metasurfaces. We note that the diffused scattering waves are caused by the destructive inference resulting from the random phase distributions of the super unit cells. To characterize the scattering reduction performance, we show the scattering gain (at the dB scale), which is defined as the backscattering from the encoded metasurface normalized by that of the bare metallic board with the same dimension, in Figure 3h. Despite the original single-frequency design at 1 THz, the scattering gain is able to reduce the scattering level significantly by at least −10 dB in the frequency range from 0.9 to 1.5 THz (despite the original single frequency design at 1 THz, the backscattering can be reduced by at least −10 dB in the frequency range from 0.9 to 1.5 THz). This example demonstrates the powerful ability of the anisotropic coding metasurface to independently manipulate the x- and y-polarized incident terahertz waves.
2-bit anisotropic coding metamaterials
Based on the design method of the 1-bit anisotropic coding metamaterial, we further introduce a 2-bit anisotropic coding metamaterial, which can provide more flexibility in manipulating the terahertz waves. The basic unit cells of 2-bit coding are able to reflect the incident waves with phase responses of 0°, 90°, 180° and 270°, which correspond to the coding elements ‘00’, ‘01’, ‘10' and ‘11’, respectively. Because the coding elements are designed to independently exhibit four distinct states under x and y polarizations, a total of 16 basic unit cells are required for the 2-bit anisotropic coding metamaterial. The structures of these 16 unit cells are shown in Figure 1e, and the geometrical parameters are provided in Supplementary Table S1. In the 2-bit case, the thickness of the polyimide layer is 25 μm. Here, the metallic square, rectangular and dumbbell-shaped structures are used to build up the four isotropic and 12 anisotropic coding elements. The six anisotropic elements in the upper triangular area can be obtained by rotating the elements in the lower triangular area by 90° in the x–y plane (Figure 1e).
To demonstrate the flexibility of the 2-bit anisotropic coding metamaterials in manipulating terahertz waves, we first encode a metasurface with the same coding sequence '00-01-10-11-00-01-10-11…' for both polarizations, and the size of the super unit cell is 2 × 2. In this case, the 2D coding matrix is written as follows:

This matrix generates the final 2-bit coding layout shown in Figure 2c. Because the adjacent super unit cells have a phase difference of 90°, Snell’s law17 indicates that the normally incident beam will be reflected at a 48° angle in the plane orthogonal to the polarization direction (Supplementary Fig. S3d). This phenomenon can be clearly observed from the 3D far-field scattering patterns presented in Figure 4a and 4b. For the x-polarized normal incidence, the terahertz beam is anomalously reflected in the direction of ( ) in the y–z plane, whereas for the y polarization, the terahertz beam is directed to the angle (
) in the y–z plane, whereas for the y polarization, the terahertz beam is directed to the angle ( ) in the x–z plane. The flexible control of terahertz reflections by polarization is further verified by the near-field distributions shown in Figure 4c and 4d. Similar to the 1-bit case, the inhomogeneity modifies the mutual coupling between the neighboring unit cells and the response to the incident wave, thus resulting in the observable disturbance of scattered fields.
) in the x–z plane. The flexible control of terahertz reflections by polarization is further verified by the near-field distributions shown in Figure 4c and 4d. Similar to the 1-bit case, the inhomogeneity modifies the mutual coupling between the neighboring unit cells and the response to the incident wave, thus resulting in the observable disturbance of scattered fields.
Simulated results for the 2-bit anisotropic coding metasurface. (a and b) 3D far-field scattering patterns for the metasurface encoded with coding matrix  under x and y polarizations, respectively. (c and d) Corresponding near-electric-field distributions Ex and Ey on the y–z and x–z cutting planes. (e) 3D far-field scattering pattern for the metasurface encoded with coding matrix
under x and y polarizations, respectively. (c and d) Corresponding near-electric-field distributions Ex and Ey on the y–z and x–z cutting planes. (e) 3D far-field scattering pattern for the metasurface encoded with coding matrix  when the incident terahertz wave is linearly polarized by 45° with respect to the x axis. (f) Variation of an anomalously reflected angle (red square line) and the axial ratio (blue circle line) as the frequency ranges from 0.8 to 1.2 THz for the same metasurface as in e. The axial ratio at each frequency point is obtained in the maximum scattering direction.
when the incident terahertz wave is linearly polarized by 45° with respect to the x axis. (f) Variation of an anomalously reflected angle (red square line) and the axial ratio (blue circle line) as the frequency ranges from 0.8 to 1.2 THz for the same metasurface as in e. The axial ratio at each frequency point is obtained in the maximum scattering direction.
The 2-bit anisotropic coding metamaterial can be utilized to design a terahertz free-background reflection-type quarter-wave plate that can produce a circularly polarized beam that bends away from a surface normal when a normally incident wave is linearly polarized by 45° with respect to the x axis. By designing the 90° reflection phase difference of each unit cell under the x and y polarizations, a circularly polarized wave is formed when the electric field is polarized along the 45° direction (with respect to the x axis). If we arrange these unit cells by a certain phase gradient along one direction, the circularly polarized wave will be reflected to an oblique angle, thus forming a background-free circularly polarized wave. This functionality is realized by encoding the metasurface with the following coding matrix:

In this case, the size of the super unit cell is 3 × 3. The corresponding 2-bit coding metasurface layout is illustrated in Figure 2d. The 3D far-field scattering pattern shown in Figure 4e reveals that the normally incident linearly polarized terahertz beam is anomalously reflected to 30° (see Supplementary Fig. S4a for details) in the x–z plane ( ) with the axial ratio as small as 1.03 at 1 THz (Figure 4f), indicating an almost ideal circularly polarized wave. With deviations from the designed frequency, the phase and amplitude responses of each unit cell will deviate from their original values. However, the well-designed reflection-type quarter-wave plate still operates in a broad frequency band as shown by the blue curve in Figure 4f. The reflected angle linearly decreases from 38° to 24.5° as the frequency changes from 0.8 to 1.2 THz, whereas the axial ratio remains below 1.26 for the entire bandwidth. Supplementary Fig. S4b shows the axial ratio from −45° to −15° in the x–z plane, which indicates that the axial ratio is <1.15 from −35° to −25°. The reflection-type quarter-wave plate with outstanding performance can be used as a high-efficiency circular polarizer and has the potential for use in interesting applications in terahertz systems.
) with the axial ratio as small as 1.03 at 1 THz (Figure 4f), indicating an almost ideal circularly polarized wave. With deviations from the designed frequency, the phase and amplitude responses of each unit cell will deviate from their original values. However, the well-designed reflection-type quarter-wave plate still operates in a broad frequency band as shown by the blue curve in Figure 4f. The reflected angle linearly decreases from 38° to 24.5° as the frequency changes from 0.8 to 1.2 THz, whereas the axial ratio remains below 1.26 for the entire bandwidth. Supplementary Fig. S4b shows the axial ratio from −45° to −15° in the x–z plane, which indicates that the axial ratio is <1.15 from −35° to −25°. The reflection-type quarter-wave plate with outstanding performance can be used as a high-efficiency circular polarizer and has the potential for use in interesting applications in terahertz systems.
In applications such as a radar system, the beam usually must be able to scan certain planes from −90° to 90°, which can be easily realized using the proposed 2-bit anisotropic coding metasurface by designing a gradient sequence ‘00-01-10-11-00-01-10-11…’ for the x polarization and its reverse sequence ‘01-00-11-10-01-00-11-10…’ for the y polarization; this sequence corresponds to the following coding matrix:

The size of the super unit cell in this case is 2 × 2. The final coding pattern containing 32 × 32 super unit cells is shown in Figure 2e. In this case, Figure 5a and 5b presents the 3D far-field scattering patterns of the encoded metasurface under the x and y polarizations, respectively, in which two identical anomalously reflected beams are observed at ±48° in the y–z plane. The patterns for the 2D plot in the y–z plane are demonstrated in Figure 5c.
Simulated 3D and 2D scattering patterns of the in-plane beam scanner. (a and b) 3D far-field scattering patterns of the metasurface encoded with coding matrix  under x and y polarizations. (d and e) 3D far-field scattering patterns of the metasurface encoded with coding matrix
under x and y polarizations. (d and e) 3D far-field scattering patterns of the metasurface encoded with coding matrix  under x and y polarizations. (c and f) 2D far-field scattering patterns of the metasurfaces encoded with coding matrices
under x and y polarizations. (c and f) 2D far-field scattering patterns of the metasurfaces encoded with coding matrices  and
and  under both polarizations in the y–z plane.
under both polarizations in the y–z plane.
Similarly, the y-polarized terahertz wave will be reflected in the direction of −22° in the y–z plane if the period of the reversed coding sequence is doubled to ‘10-10-01-01-00-00-11-11-10-10-01-01-00-00-11-11-…’ and the coding sequence remains unchanged for the x polarization. This functionality can be realized by encoding the metasurface with the 8 × 8 coding matrix:

The coding pattern containing 32 × 32 super unit cells (with size 2 × 2) is shown in Figure 2f, and the corresponding 3D far-field scattering patterns under the x and y polarizations are illustrated in Figure 5d and 5e, respectively. In this case, the y-polarized terahertz wave is reflected to −22° in the y–z plane, whereas the anomalously reflected beam under the x polarization is unaffected (Figure 5f). Note that the intensity of the −22° reflected beam (red curve) has been normalized to the maximum value of the beam reflected by the metallic board tilted at 11° along the y axis. Again, the difference in the beam intensities of the anomalously reflected beams under the x and y polarizations may be caused by unpredictable phase responses produced by interactions among the different unit cells. In addition, we note that the eigenmodes under the x and y polarizations are transverse-electric and transverse-magnetic modes, respectively, which could also contribute to discrepancies. Overall, the deflection angle in both cases is strongly correlated with the generalized Snell’s law.
Results and discussion
To experimentally validate the performance of the anisotropic coding metasurfaces, three samples (two 1-bit and one 2-bit) are fabricated using standard photolithography processes as demonstrated in Figure 6a and 6b and Supplementary Fig. S5a and S5b, respectively, which correspond to the coding layouts shown in Figure 2a–2c. During the fabrication of the terahertz anisotropic coding metasurfaces, a 180-nm-thick gold layer was deposited on a silicon wafer by electron beam evaporation to serve as the metallic background. A spin-coating process then enables the uniform deposition of the liquid polyimide (Yi Dun New Materials, Suzhou, China) on the gold layer, which was then solidified on a hot plate at 80, 120, 180 and 250 °C for 5, 5, 5 and 20 min, respectively. Considering the viscosity of the polyimide and the minimum spin speed, these spin-coating and curing processes must be repeated two and three times to produce final polyimide layers with thicknesses of 20 and 25 μm, respectively. Next, another Ti/Au layer (10/180 nm) was deposited by electron beam evaporation and followed by the standard photolithography, and a lift-off process was then used to form the final metallic pattern. The sample can be easily peeled from the wafer substrate because of the poor adhesion between the gold and silica layers (grown on the silicon wafer).
Photographs of the fabricated sample and schematics of the experimental setup. (a) Freestanding sample released from the silicon wafer. (b) Optical microscopy image of the sample encoded with coding matrix  . (c and d) Schematics of the experimental configurations for the rotatory THz–TDS and theta-to-theta THz-TDS systems.
. (c and d) Schematics of the experimental configurations for the rotatory THz–TDS and theta-to-theta THz-TDS systems.
Each sample covers an area of 15 × 15 mm2, which is sufficiently large to accommodate the plane-wave-like incident beam with a diameter of ~5 mm. The freestanding sample (Figure 6a) is so flexible that it can be wrapped on any object with a curved surface, thus indicating its potential use in applications such as in conformal cloaking38, curved focusing lenses and beam splitters at terahertz frequencies. Figure 6b depicts a zoomed image of the 1-bit coding sample (Figure 2b) taken by an optical microscope (VHX-5000, Keyence Company, Beijing, China). Two terahertz measurement systems (rotatory THz-TDS and theta-to-theta THz-TDS) were employed to measure the deflected angle and diffused scattering of the fabricated sample, respectively.
A sketch of the experimental setup of the rotatory THz-TDS system is presented in Figure 6c. Here, a pair of fiber-based terahertz photoconductive switches (Model TR4100-RX1, API Advanced Photonix, Ann Arbor, MI, USA) was used to generate and detect the time-domain terahertz pulses. The position of the transmitter was fixed, whereas the receiver was placed on a strip-shaped holder that can be rotated around the central metallic cylinder (see Supplementary Fig. S5c). The sample was attached to a metallic board mounted on the central cylinder. The distances between both the transmitter and receiver to the sample were 23 cm, and the angle between them could be scanned from 24° to 90° in the y–z plane. Both the THz transmitter and receiver were optically excited by a commercial ultrafast erbium fiber laser system (T-Gauge, API Advanced Photonix), thus enabling the THz transmitter and receiver to operate from 0.3 to 3.0 THz. The deflected beam scattered from the sample was recorded every 5° from 25° to 90° except at 80° and 85° because the signals measured at such large oblique angles are weak. The signal reflected from an opaque gold film was recorded and used as a reference for all of the incident angles.
The schematic diagram of the experimental setup for the theta-to-theta THz-TDS system (Zomega Z-3, East Greenbush, NY, USA) is presented in Figure 6d. The sample, which is attached to a sample holder, was located on a rotatory stage and could be automatically rotated from 20° to 90°. A parabolic mirror located on another independent rotatory stage was used to normally reflect the terahertz beam (reflected from the sample) back to sample because the parabolic mirror could automatically aim at the specular reflection direction of the incident beam. The signal was then reflected to the receiver by several mirrors. In this measurement, we recorded the terahertz wave reflected from the opaque gold film at 0°, 20°, 40° and 60° as references. A detailed description of the theta-to-theta THz-TDS system can be found in Supplementary Fig. S5d.
The measured reflection amplitudes with respect to the receiving angle of the 1-bit coding metasurface encoded with coding matrix  (Supplementary Fig. S5a) under x and y polarizations in the y–z and x–z planes, respectively, are provided in Figure 7a. Note that all of the measurement data were plotted at 1 THz after a data smoothing treatment to eliminate the background noise. Two nearly identical peaks can be clearly observed between 40° and 60°, with the maximum values appearing at ~51° for both polarizations, indicating that the normally incident terahertz beam is reflected to a 51° angle under both polarizations. We note that because the angles of the two deflected beams in this design are symmetrical with respect to the x–z or y–z plane, only the deflected angles from 0° to 90° are measured in the experiments. The measured result (51°) is consistent with the theoretical result (48.5°). We note that the maximum amplitudes of the anomalous reflections (between 0.5 and 0.53) from the above measurements are slightly larger than those in the simulations (0.456). This discrepancy could have been caused by inaccuracies in the thickness of the PI layer or the inevitable tolerance in the structural dimensions during fabrication, both of which could lead to a distorted scattering pattern and result in higher or lower radiations in certain directions.
(Supplementary Fig. S5a) under x and y polarizations in the y–z and x–z planes, respectively, are provided in Figure 7a. Note that all of the measurement data were plotted at 1 THz after a data smoothing treatment to eliminate the background noise. Two nearly identical peaks can be clearly observed between 40° and 60°, with the maximum values appearing at ~51° for both polarizations, indicating that the normally incident terahertz beam is reflected to a 51° angle under both polarizations. We note that because the angles of the two deflected beams in this design are symmetrical with respect to the x–z or y–z plane, only the deflected angles from 0° to 90° are measured in the experiments. The measured result (51°) is consistent with the theoretical result (48.5°). We note that the maximum amplitudes of the anomalous reflections (between 0.5 and 0.53) from the above measurements are slightly larger than those in the simulations (0.456). This discrepancy could have been caused by inaccuracies in the thickness of the PI layer or the inevitable tolerance in the structural dimensions during fabrication, both of which could lead to a distorted scattering pattern and result in higher or lower radiations in certain directions.
Experimental results for anisotropic coding metasurfaces encoded with three different coding matrices. (a and d) Amplitudes of the reflections versus the receiving angle at 1 THz for the metasurfaces encoded with coding matrices  and
and  under both polarizations. (b) Amplitudes of the reflections with respect to the receiving angle at 1 THz for the 1-bit anisotropic metasurface encoded with coding matrix
under both polarizations. (b) Amplitudes of the reflections with respect to the receiving angle at 1 THz for the 1-bit anisotropic metasurface encoded with coding matrix  under x polarization. (c) Scattering gains for the same metasurface as in b under y polarization measured at 0°, 20°, 40° and 60°. (e) Reflection amplitudes from 0.4 to 1.8 THz for the same metasurface as in d under x polarization when the receiver scans from 25° to 90°.
under x polarization. (c) Scattering gains for the same metasurface as in b under y polarization measured at 0°, 20°, 40° and 60°. (e) Reflection amplitudes from 0.4 to 1.8 THz for the same metasurface as in d under x polarization when the receiver scans from 25° to 90°.
For the other 1-bit anisotropic coding metasurface encoded with coding matrix  (Figure 6b), we provide the measured reflection amplitude versus the receiving angle when the surface is normally illuminated with the x-polarized terahertz beam (Figure 7b). A similar scattering pattern to that shown in Figure 7a is obtained despite the different coding sequences. When the polarization of the incident beam turns 90° toward the y axis, however, the normally incident beam is evenly scattered in many directions in the upper half-space and results in low reflection in specular reflection directions, which can be verified by the scattering gains under the different specular reflection angles at 0°, 20°, 40° and 60° in Figure 7c. The reflections under a normal incidence remain below −10 dB from 0.9 to 1.2 THz, and this low-reflection band is further expanded to 0.5 THz (from 0.88 to 1.38 THz) under the specular reflection angle of 20°. The random scattering performance deteriorates for larger specular reflection angles because the current measurement setup only supports transverse-magnetic polarization (the electric field is horizontally polarized). At oblique incidences, the wave vector is no longer parallel to the unit cell plane, which leads to the appearance of higher order modes and influences the reflection responses of unit cells39.
(Figure 6b), we provide the measured reflection amplitude versus the receiving angle when the surface is normally illuminated with the x-polarized terahertz beam (Figure 7b). A similar scattering pattern to that shown in Figure 7a is obtained despite the different coding sequences. When the polarization of the incident beam turns 90° toward the y axis, however, the normally incident beam is evenly scattered in many directions in the upper half-space and results in low reflection in specular reflection directions, which can be verified by the scattering gains under the different specular reflection angles at 0°, 20°, 40° and 60° in Figure 7c. The reflections under a normal incidence remain below −10 dB from 0.9 to 1.2 THz, and this low-reflection band is further expanded to 0.5 THz (from 0.88 to 1.38 THz) under the specular reflection angle of 20°. The random scattering performance deteriorates for larger specular reflection angles because the current measurement setup only supports transverse-magnetic polarization (the electric field is horizontally polarized). At oblique incidences, the wave vector is no longer parallel to the unit cell plane, which leads to the appearance of higher order modes and influences the reflection responses of unit cells39.
For the 2-bit anisotropic metasurface encoded by matrix  (Supplementary Fig. S5b), the measured reflection amplitudes from 25° to 90° for the x polarization (in the y–z plane) and y polarization (in the x–z plane) are illustrated in Figure 7d, which shows that the normally incident beam is reflected at a 52° angle in the y–z plane (for the x polarization) and the x–z plane (for the y polarization). Figure 7e further demonstrates the measured reflection amplitudes from 0.4 to 1.8 THz in the 2-bit case (same pattern as Figure 7d) under the x polarization when the receiver scans from 25° to 90°. We note that the blue curve in Figure 7d is actually extracted from all of the curves in Figure 7e at 1 THz as marked by the vertical light-blue line. Significant anomalous reflection peaks are detected from 35° to 75°, and these reflection peaks shift to smaller angles with increasing frequencies, which is consistent with the generalized Snell’s law. The consistency between the experimental and simulation results clearly demonstrates both the functionality and performance of the 1-bit and 2-bit anisotropic coding metamaterials.
(Supplementary Fig. S5b), the measured reflection amplitudes from 25° to 90° for the x polarization (in the y–z plane) and y polarization (in the x–z plane) are illustrated in Figure 7d, which shows that the normally incident beam is reflected at a 52° angle in the y–z plane (for the x polarization) and the x–z plane (for the y polarization). Figure 7e further demonstrates the measured reflection amplitudes from 0.4 to 1.8 THz in the 2-bit case (same pattern as Figure 7d) under the x polarization when the receiver scans from 25° to 90°. We note that the blue curve in Figure 7d is actually extracted from all of the curves in Figure 7e at 1 THz as marked by the vertical light-blue line. Significant anomalous reflection peaks are detected from 35° to 75°, and these reflection peaks shift to smaller angles with increasing frequencies, which is consistent with the generalized Snell’s law. The consistency between the experimental and simulation results clearly demonstrates both the functionality and performance of the 1-bit and 2-bit anisotropic coding metamaterials.
Conclusions
In this paper, the functionality of 1-bit and 2-bit anisotropic coding metamaterials composed of squares and dumbbell-shaped structures is theoretically and experimentally demonstrated at terahertz frequencies, and the results indicate that these metamaterials exhibit multiple functionalities under different polarizations. Our findings show that the anisotropic coding metasurface has a strong ability to independently control terahertz waves under different polarizations. For example, we demonstrated that under the normal illuminance of x-polarized terahertz waves, a 1-bit anisotropic coding metasurface can produce anomalous reflections along the direction θ=sin−1(λ/Γ) from a surface normal; however, under y polarization, the same anisotropic coding metasurface will randomly scatter the terahertz waves and generate a diffusion pattern in the upper half-space. The anisotropic coding metasurface allows us to write two completely different coding sequences on a single metasurface and therefore realize dual functions in the manipulation of beam patterns by simply changing the polarization state.
Although the concept of an anisotropic coding metasurface is implemented at the terahertz frequency, it is also valid for other frequency spectra, such as microwave and visible light. Thus, we predict that such metasurfaces will have the potential for use in a variety of applications that utilize frequencies from microwave to visible. In the microwave regime, one can alter the radiation direction, or the scattering pattern, of the antenna by rotating the polarization direction, which provides another degree of freedom in designing reconfigurable antennas. With the 2-bit anisotropic coding metasurface, the free-background reflection-type quarter-wave plate could be realized by designing a 90° phase difference under the x and y polarizations for each coding particle and arranging the coding particles with a gradient phase along a certain direction. Such a high-efficiency circular polarizer is desirable for antenna designs because it not only converts the normally incident wave from a linear polarization to circular polarization but can also steer the beam in a certain direction. In the terahertz regime, the anisotropic coding metasurface can be used to design a beam splitter (illustrated in Figure 3c) that can demultiplex (or separate) the terahertz signal modulated with two orthogonal polarizations. This technique will double the information carried on a single terahertz beam and could be utilized to enhance the transmission rate of future ultrahigh-speed wireless communications. In the visible light range, the dual-polarization feature of the anisotropic coding metasurface may be utilized to increase the storage density of current storage media, such as Blu-ray Discs, because each storage dot carrying two independent datum can be read by a laser generated with two orthogonal polarizations. In addition, digital holography could also benefit from this technique by encoding two different images with orthogonal polarizations into one, thus enabling the realization of 3D holographic displays.
We should also note that the flexible nature of the proposed design offers another degree of freedom in designing coding metasurfaces because the abrupt phase change of the coding particles can be combined with the gradient phase delay resulting from the geometry of the object to which the flexible metasurface is attached. Thus, the phase coverage of 2π is not necessarily required by the coding particle when designing a beam-steering reflector or focusing lens because the curved shape of the flexible metasurface could also contribute to the required phase distribution, which may reduce the complexity of designing the coding particles. We believe that the outstanding dual-functional performance and various features of this design (for example, ultrathin thickness, flexibility and easy fabrication) demonstrates the potential uses of anisotropic coding metasurfaces in low-cost terahertz devices as well as the broad potential applications of such surfaces in microwave and visible frequencies.
Author contributions
SL conducted the analytical modeling, numerical simulations, sample fabrication, and measurements. TJC, as the principal investigator of the project, conceived the idea, suggested the designs, and planned, coordinated and supervised the work. XW, WXT, XYZ and HY ran numerical simulations, and QX, DB, LD, CO, HFM, WXJ, JH, WLZ and QC participated in the sample fabrication and measurements. All of the authors discussed the theoretical and numerical aspects, interpreted the results and contributed to the preparation and writing of the manuscript.
References
Smith DR, Padilla WJ, Vier DC, Nemat-Nasser SC, Schultz S . Composite medium with simultaneously negative permeability and permittivity. Phys Rev Lett 2000; 84: 4184–4187.
Liu RP, Cui TJ, Huang D, Zhao B, Smith DR . Description and explanation of electromagnetic behaviors in artificial metamaterials based on effective medium theory. Phys Rev E 2007; 76: 026606.
Li ZF, Aydin K, Ozbay E . Determination of the effective constitutive parameters of bianisotropic metamaterials from reflection and transmission coefficients. Phys Rev E 2009; 79: 026610.
Shelby RA, Smith DR, Schultz S . Experimental verification of a negative index of refraction. Science 2001; 292: 77–79.
Shin H, Fan SH . All-angle negative refraction for surface plasmon waves using a metal-dielectric-metal structure. Phys Rev Lett 2006; 96: 239903.
Pendry JB . Negative refraction makes a perfect lens. Phys Rev Lett 2000; 85: 3966–3969.
Liu R, Ji C, Mock JJ, Chin JY, Cui TJ et al. Broadband ground-plane cloak. Science 2009; 323: 366–369.
Schurig D, Mock JJ, Justice BJ, Cummer SA, Pendry JB et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006; 314: 977–980.
Magnus F, Wood B, Moore J, Morrison K, Perkins G et al. A d. c. magnetic metamaterial. Nat Mater 2008; 7: 295–297.
Ma HF, Cui TJ . Three-dimensional broadband ground-plane cloak made of metamaterials. Nat Commun 2010; 1: 21.
Cui TJ, Smith DR, Liu RP . Metamaterials: Theory, Design, and Applications. New York: Springer Science & Business Media. 2009.
Ma HF, Cui TJ . Three-dimensional broadband and broad-angle transformation-optics lens. Nat Commun 2010; 1: 124.
Kabashin AV, Evans P, Pastkovsky S, Hendren W, Wurtz GA et al. Plasmonic nanorod metamaterials for biosensing. Nat Mater 2009; 8: 867–871.
Cheng Q, Cui TJ, Jiang WX, Cai BG . An omnidirectional electromagnetic absorber made of metamaterials. New J Phys 2010; 12: 063006.
Holloway CL, Kuester EF, Gordon JA, O’Hara J, Booth J et al. An overview of the theory and applications of metasurfaces: The two-dimensional equivalents of metamaterials. IEEE Antennas Propag 2012; 54: 10–35.
Aieta F, Genevet P, Yu NF, Kats MA, Gaburro Z et al. Out-of-plane reflection and refraction of light by anisotropic optical antenna metasurfaces with phase discontinuities. Nano Lett 2012; 12: 1702–1706.
Yu NF, Genevet P, Kats MA, Aieta F, Tetienne J-P et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011; 334: 333–337.
Liu LX, Zhang XQ, Kenney M, Su XQ, Xu NN et al. Broadband metasurfaces with simultaneous control of phase and amplitude. Adv Mater 2014; 26: 5031–5036.
Chen XZ, Huang LL, Mühlenbernd H, Li GX, Bai BF et al. Dual-polarity plasmonic metalens for visible light. Nat Commun 2012; 3: 1198.
Zheng GX, Mühlenbernd H, Kenney M, Li GX, Zentgraf T et al. Metasurface holograms reaching 80% efficiency. Nat Nanotechnol 2015; 10: 308–312.
Chen WT, Yang KY, Wang CM, Huang YW, Sun G et al. High-efficiency broadband meta-hologram with polarization-controlled dual images. Nano Lett 2014; 14: 225–230.
Ni XJ, Kildishev AV, Shalaev VM . Metasurface holograms for visible light. Nat Commun 2013; 4: 2807.
Kats MA, Genevet P, Aoust G, Yu NF, Blanchard R et al. Giant birefringence in optical antenna arrays with widely tailorable optical anisotropy. Proc Natl Acad Sci USA 2012; 109: 12364–12368.
Ni XJ, Ishii S, Kildishev AV, Shalaev VM . Ultra-thin, planar, Babinet-inverted plasmonic metalenses. Light Sci Appl 2013; 2: e72.
Yao Y, Kats MA, Genevet P, Yu NF, Song Y et al. Broad electrical tuning of graphene-loaded plasmonic antennas. Nano Lett 2013; 13: 1257–1264.
Li YB, Wan X, Cai BG, Cheng Q, Cui TJ . Frequency-controls of electromagnetic multi-beam scanning by metasurfaces. Sci Rep 2014; 4: 6921.
Zhang J, Mei ZL, Zhang WR, Yang F, Cui TJ . An ultrathin directional carpet cloak based on generalized Snell's law. Appl Phys Lett 2013; 103: 151115.
Sun SL, He Q, Xiao SY, Xu Q, Li X et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat Mater 2012; 11: 426–431.
Shen XP, Yang Y, Zang YZ, Gu JQ, Han JG et al. Triple-band terahertz metamaterial absorber: Design, experiment, and physical interpretation. Appl Phys Lett 2012; 101: 154102.
Chen HT, Padilla WJ, Cich MJ, Azad AK, Averitt RD et al. A metamaterial solid-state terahertz phase modulator. Nat Photon 2009; 3: 148–151.
Yu NF, Aieta F, Genevet P, Kats MA, Gaburro Z et al. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett 2012; 12: 6328–6333.
Monticone F, Estakhri NM, Alù A . Full control of nanoscale optical transmission with a composite metascreen. Phys Rev Lett 2013; 110: 203903.
Ni XJ, Emani NK, Kildishev AV, Boltasseva A, Shalaev VM . Broadband light bending with plasmonic nanoantennas. Science 2012; 335: 427.
Della Giovampaola C, Engheta N . Digital metamaterials. Nat Mater 2014; 13: 1115–1121.
Cui TJ, Q MQ, Wan X, Zhao J, Cheng Q . Coding metamaterials, digital metamaterials and programmable metamaterials. Light Sci Appl 2014; 3: e218.
Gao LH, Cheng Q, Yang J, Ma SJ, Zhao J et al. Broadband diffusion of terahertz waves by multi-bit coding metasurfaces. Light Sci Appl 2015; 4: e324.
Liang LJ, Qi MQ, Yang J, Shen XP, Zhai JQ et al. Anomalous terahertz reflection and scattering by flexible and conformal coding metamaterials. Adv Opt Mater 2015; 3: 1374–1380.
Liu S, Xu HX, Zhang HC, Cui TJ . Tunable ultrathin mantle cloak via varactor-diode-loaded metasurface. Opt Express 2014; 22: 13403–13417.
Ye YQ, Jin Y, He SL . Omnidirectional, polarization-insensitive and broadband thin absorber in the terahertz regime. J Opt Soc Am B 2010; 27: 498–504.
Acknowledgements
This work was supported by the National Science Foundation of China (61571117, 61522106, 61138001, 61302018 and 61401089), Natural Science Foundation of the Jiangsu Province (BK2012019), and the 111 Project (111-2-05).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications' website .
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Liu, S., Cui, T., Xu, Q. et al. Anisotropic coding metamaterials and their powerful manipulation of differently polarized terahertz waves. Light Sci Appl 5, e16076 (2016). https://doi.org/10.1038/lsa.2016.76
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2016.76
Keywords
This article is cited by
-
Single-Row Coding Metasurface for Bi-directional Beam Multiplexing in Mid-infrared Regime
Plasmonics (2023)
-
A numerical investigation study on tunable graphene-squared pixel array-based infrared polarizer
Applied Physics B (2023)
-
Numerical investigation of the tunable polarizer using gold array and graphene metamaterial structure for an infrared frequency range
Applied Physics B (2022)
-
Tunable frequency selective surface using crossed shaped graphene metasurface geometry for far infrared frequency spectrum
Applied Physics B (2022)
-
Single-pixel polarimetric direction of arrival estimation using programmable coding metasurface aperture
Scientific Reports (2021)