Abstract
Simultaneous Kerr comb formation and second-harmonic generation with on-chip microresonators can greatly facilitate comb self-referencing for optical clocks and frequency metrology. Moreover, the presence of both second- and third-order nonlinearities results in complex cavity dynamics that is of high scientific interest but is still far from being well-understood. Here, we demonstrate that the interaction between the fundamental and the second-harmonic waves can provide an entirely new way of phase matching for four-wave mixing in optical microresonators, enabling the generation of optical frequency combs in the normal dispersion regime under conditions where comb creation is ordinarily prohibited. We derive new coupled time-domain mean-field equations and obtain simulation results showing good qualitative agreement with our experimental observations. Our findings provide a novel way of overcoming the dispersion limit for simultaneous Kerr comb formation and second-harmonic generation, which might prove to be especially important in the near-visible to visible range where several atomic transitions commonly used for the stabilization of optical clocks are located and where the large normal material dispersion is likely to dominate.
Similar content being viewed by others
Introduction
Comb-based optical frequency metrology and atom clocks have pushed the measurement of time and frequency to unprecedented precision in recent decades1. The recently emerged miniature microresonator-based optical frequency combs (microcombs) can potentially bring this technology from the laboratory to portable applications2, 3, 4, 5, 6, 7, 8, 9, 10. Microcomb generation is a technique that converts a single-frequency laser pump to a broadband comb source using a high-quality-factor microresonator. The basic mechanism is based on the cavity-enhanced Kerr effect arising from the third-order optical nonlinearity. Rich dynamics have been observed in the comb generation process, such as chaos11, mode-locking12, 13, 14,15, 16, 17, temporal bright and dark solitons18, 19, 20, 21, 22, discrete phase steps23 and Cherenkov radiation24. In addition to ultra-wideband comb generation, the second-harmonic conversion of a fraction of the frequency lines is another key step to achieving a fully stabilized comb source based on comb self-referencing. Simultaneous comb formation and second-harmonic generation with a single microresonator will greatly facilitate this procedure because it avoids the need for additional second-order nonlinear elements. This can potentially be achieved by taking advantage of both the second- and third-order nonlinearities in some microresonator platforms25, 26. Nevertheless, compared with a purely third-order system, the participation of the second-order nonlinearity can affect the comb self-starting and mode-locking behaviors, resulting in complex dynamics that are far from well-understood.
In this work, we report a nonlinear mode-coupling mechanism that can significantly change the comb dynamics in microresonators with both second- and third-order nonlinearities. The mode coupling arises from the interaction between the fundamental and the second-harmonic waves and permits modulational instability (MI) in the normal dispersion region under conditions where comb formation is typically prohibited in the absence of mode coupling. In both experiments and numerical simulations, we demonstrate simultaneous second-harmonic generation and broadband mode-locked comb generation in a microresonator which shows normal group velocity dispersion for the fundamental wave. Our work reveals, for the first time, to our knowledge, that second-harmonic mode coupling can provide an entirely new way of fulfilling phase-matching for four-wave mixing in the normal dispersion regime and may also alter the nonlinear dynamics in the anomalous dispersion regime.
Materials and methods
Silicon nitride microring fabrication
The microresonator we use is a silicon nitride (SiN) microring embedded in silicon dioxide; this is one of the microrings used in our previous report on mode-locked dark pulses20. The microring has a radius of 100 μm, corresponding to a free spectral range (FSR) of ~231 GHz, and a loaded quality factor of 8.6 × 105. The cross-section of the microring waveguide is 2 μm × 550 nm, and its measured group velocity dispersion in the C-band is 186.9 ps2 km−1, that is, strongly normal. Both a through-port waveguide and a drop-port waveguide coupled to the microring are fabricated. The device fabrication process is as follows. An undercladding layer of 3 μm thermal oxide is grown on a silicon wafer in an oxidation tube at 1100 °C. Using low-pressure chemical vapor deposition, a 550-nm SiN film is deposited at 800 °C on the oxidized wafer. A negative hydrogen silsesquioxane resist is used to pattern the waveguide and resonator via an electron beam lithography system at 100 kV. After developing in tetramethylammonium hydroxide solution, the hydrogen silsesquioxane pattern is transferred to the SiN film using reactive ion etching. Then, a 3.5-μm-thick low-temperature oxide film, which serves as an upper cladding, is deposited at 400 °C followed by an annealing step undertaken at 1100 °C in an N2 atmosphere.
Comb generation and characterization
A detailed schematic representation of our experimental setup for comb generation is shown in Figure 1a. An infrared (IR) tunable laser source in the C-band is amplified and pumps the SiN microring. The light from the microring chip is split into three branches. From top to bottom, the first branch measures the total power in the fundamental IR spectral range, the second branch measures the IR comb power excluding the pump line (the pulse shaper acts as a band-reject filter), and the third branch measures the second-harmonic power (the IR power is blocked by a glass filter). The Pound–Drever–Hall (PDH) signal is also measured to monitor the effective pump-resonance detuning when the optical signal is analyzed at the through port18 (setup not shown).
Second-harmonic-assisted comb generation in a normal dispersion SiN microring resonator. (a) Experimental setup. The inset shows the microscope image of the microring with second-harmonic radiation. (b) Transition curves when the pump laser scans across the resonance from shorter to longer wavelengths. From top to bottom: total IR power at the through port, total IR power at the drop port, IR comb power excluding the pump line at the drop port, second-harmonic power at the drop port, PDH signal (the measurement setup is not shown in a). (c) Zoomed-in details in the gray region marked in b. The region marked in a blue dashed box shows a millisecond timescale oscillation. The drop-port comb spectra at different detuning stages (I, II and III) are shown in the following Figure 2.
To probe the phase coherence of the generated frequency comb and to investigate its time-domain characteristics, we have used spectral line-by-line shaping in combination with intensity correlation measurements12, 13. The dispersion of the fiber link between the output of the microring chip and the input of the intensity correlator is compensated; thus, we can retrieve the comb spectral phase by compressing the comb to a transform-limited pulse. The time-domain waveform can then be reconstructed through Fourier synthesis based on the amplitude and phase information of the comb. Self-referenced cross-correlation is also measured for comparison.
In diagnosing the comb-formation dynamics, we have introduced a method of fiber comb spectroscopy to measure the relative positions of the microresonator resonances in comb operation with respect to the comb lines (that is, hot-cavity detuning). The principle will be explained in detail together with the results in a later section.
Theoretical model
In microresonators with only third-order Kerr nonlinearity, the evolution of the intracavity field can generally be described by the mean-field Lugiato–Lefever (L–L) equation27, 28. When there are simultaneous second- and third-order nonlinearities, a second-harmonic wave may be generated, with the fundamental and second-harmonic waves coupled to each other through second-order nonlinearity. To understand the underlying physics of our experiments, a theoretical model incorporating coupled L–L equations is developed (see Supplementary Section 2 for the equation derivation29, 30). In particular, we find that the intracavity fields at the fundamental and second-harmonic wavelengths obey the following coupled equations:


Here, E1 and E2 are the intracavity amplitudes of the fundamental and second-harmonic waves scaled, such that  represents the power flow; z is the propagation distance in the cavity; τ is the time; α1 and α2 are the averaged loss per unit length, including the intrinsic loss and external coupling loss; δ1 is related to the pump-resonance detuning by
represents the power flow; z is the propagation distance in the cavity; τ is the time; α1 and α2 are the averaged loss per unit length, including the intrinsic loss and external coupling loss; δ1 is related to the pump-resonance detuning by  , with ω0 the resonance frequency, ωp the pump frequency, tR the round-trip time for the fundamental wave and L the round-trip length;
, with ω0 the resonance frequency, ωp the pump frequency, tR the round-trip time for the fundamental wave and L the round-trip length;  and
and  are the group velocity dispersions;
are the group velocity dispersions;  is the phase mismatch;
is the phase mismatch;  is the group velocity mismatch; γ1 and γ2 are the nonlinear coefficients of self-phase modulation; γ12 and γ21 are the nonlinear coefficients of cross-phase modulation; κ is the second-order coupling coefficient;
is the group velocity mismatch; γ1 and γ2 are the nonlinear coefficients of self-phase modulation; γ12 and γ21 are the nonlinear coefficients of cross-phase modulation; κ is the second-order coupling coefficient;  is the coupling coefficient between the pump and the intracavity field, where θ1 is the waveguide-resonator power coupling ratio for the fundamental wave; and Ein is the amplitude of the pump.
is the coupling coefficient between the pump and the intracavity field, where θ1 is the waveguide-resonator power coupling ratio for the fundamental wave; and Ein is the amplitude of the pump.
Results and discussion
Second-harmonic-assisted comb generation
Although second-order nonlinearity is absent from bulk amorphous SiN material, it can exist in SiN thin films and waveguides due to surface effects or due to silicon nanocrystals that form in the fabrication process31, 32, 33, 34, 35. Indeed, in our experiments, we find that the selected cavity resonances yield a significant generation of light at the second harmonic of the pump laser. To generate a frequency comb, the wavelength of the pump laser is tuned to ~1543 nm. Specifically, the laser sweeps from a shorter wavelength to a longer wavelength across the microring resonance at a relatively slow speed of 0.5 nm s−1. The on-chip pump power is ~0.4 W. Figure 1b shows the transmission curves measured at the output of the microring chip, with the zoom-in details shown in Figure 1c. Because of the resonance shift caused by the Kerr and thermo-optic effects, the total power transmission has a typical triangular shape36. Furthermore, a signal at the second harmonic can readily be detected as the pump laser tunes into resonance. Transition steps, which correspond to the switching of the comb dynamics, can also be clearly observed in transmission curves corresponding to both the fundamental and second-harmonic wavelengths. The PDH signal shown in the bottom panel of Figure 1b indicates that the pump laser in comb operation is always effectively blue-detuned with respect to the shifted resonance.
The optical power shows an oscillation in the region marked with a blue dashed box in Figure 1c. The oscillation occurs on a millisecond timescale and increases in speed as the pump laser is tuned to the red. Oscillation and self-pulsing caused by thermal nonlinearity have been observed in a variety of microresonator platforms37, 38, 39, 40, 41, 42. They generally require either two nonlinear mechanisms with different signs or two excited modes that interact with each other37, 38. For our microring, although two nonlinear processes with different response times were observed previously in microheater-actuated tuning experiments43, the two processes appear to have the same sign. We believe that the oscillation may involve the interplay between the pump and comb modes with a resonant mode at the second-harmonic frequency. As supporting evidence, we note that (i) the switching of the comb power and second-harmonic power are both observed within the oscillation in Figure 1c and (ii) we did not see the thermal oscillations when pumping resonances of the same microring that do not show second-harmonic generation—including those where we previously observed the linear-mode-coupling initiation of the comb. In the current paper, we focus our investigations in the region where the oscillation vanishes with the pump laser further tuned to the red and leave the development of a detailed oscillation model for future work.
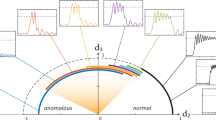
The optical spectra measured in a range spanning more than one octave at different pump detunings are shown in Figure 2a (the increase on the low frequency side is due to the optical spectrum analyzer background, not the comb lines). Zoomed-in spectra of the fundamental and second-harmonic waves are shown in Figure 2b and 2c, respectively. Frequency combs can clearly be observed both around the IR pump and its second harmonic. The comb formation can be divided into three different stages as follows. At detuning stage I (see Figure 1c), only the second harmonic of the pump can be observed, and no comb is generated. With the detuning changed to stage II, a narrow-band fundamental IR comb spaced by 1 FSR is generated, and a few second-harmonic lines appear. The spacing between the second-harmonic lines is equal to that of the fundamental comb. The IR comb then transitions to a state with a much broader spectrum at detuning stage III. A slight change of the second-harmonic spectra is also observed in the transition. The IR comb shows very low-intensity noise (below the noise background of the measuring electrical spectrum analyzer) in most parts of the pump-sweeping process, except in a small region right before transitioning to stage III, where an increased intensity noise is observed. (The intensity noise is not revealed in the transmission curves in Figure 1c due to the smoothing function of the oscilloscope; see Supplementary Section 1 for traces captured with a different data acquisition mode.) Note that the low intensity noise of the broadband comb at stage III generally corresponds to mode-locking and the formation of temporal structures in the cavity15, 16, 17, 18, 19, 20.
Drop-port comb spectra at the different detuning stages marked in Figure 1c. (a) Spectra measured in a range of more than one octave (the increase on the low-frequency side is due to the optical spectrum analyzer background). (b) Zoomed-in IR spectra. (c) Zoomed-in second-harmonic spectra.
Reciprocal bright and dark pulses
Figure 3a and 3b show, respectively, the amplitude and phase of the comb lines in the C-band at stage III (here, the comb phase follows the sign convention generally used in ultrafast optics44, that is, the field of each comb line is represented by  , where A is the amplitude, ω is the angular frequency and φ is the phase). The only difference between the optical fields at the through and drop ports is the complex amplitude of the pump line. All the comb lines at the drop port arise from coupling out of the microresonator. Therefore, the complex spectrum at the drop port should be the same as that in the cavity, as should the time-domain waveform. However, the pump line at the through port corresponds to the coherent superposition of the pump transmitted directly from the input waveguide and the pump component coupled out of the cavity. Because the complex pump field at the through port differs from that in the cavity, the time-domain waveforms at the through port and inside the cavity also differ20. For the specific example described here, the pump lines at the through and drop ports have very close power levels (difference<1 dB) but have a large phase difference (~2.4 rad). Figure 3c and 3d show the reconstructed waveforms at the through and drop ports, respectively. The drop-port (intracavity) waveform is a dark pulse, which has been previously reported in normal dispersion microresonators20. The dark pulse width is ~394 fs. Interestingly, the through-port waveform shows a nice bright pulse (width ~275 fs). Note that the bright pulse has a high background level, which is limited by the cancellation ratio between the input pump and the dark pulse background in the through-port waveguide. The background level can be adjusted by changing the coupling condition between the microresonator and the through-port waveguide. A close-to-zero background can be achieved for the critical coupling condition. This way to tailor the pulse shape may be potentially useful for applications that require ultrashort bright pulses. The self-referenced cross-correlation is also measured to further verify the time-domain waveforms20, and the results are consistent with those reconstructed through spectral line-by-line shaping (see Figure 3e and 3f).
, where A is the amplitude, ω is the angular frequency and φ is the phase). The only difference between the optical fields at the through and drop ports is the complex amplitude of the pump line. All the comb lines at the drop port arise from coupling out of the microresonator. Therefore, the complex spectrum at the drop port should be the same as that in the cavity, as should the time-domain waveform. However, the pump line at the through port corresponds to the coherent superposition of the pump transmitted directly from the input waveguide and the pump component coupled out of the cavity. Because the complex pump field at the through port differs from that in the cavity, the time-domain waveforms at the through port and inside the cavity also differ20. For the specific example described here, the pump lines at the through and drop ports have very close power levels (difference<1 dB) but have a large phase difference (~2.4 rad). Figure 3c and 3d show the reconstructed waveforms at the through and drop ports, respectively. The drop-port (intracavity) waveform is a dark pulse, which has been previously reported in normal dispersion microresonators20. The dark pulse width is ~394 fs. Interestingly, the through-port waveform shows a nice bright pulse (width ~275 fs). Note that the bright pulse has a high background level, which is limited by the cancellation ratio between the input pump and the dark pulse background in the through-port waveguide. The background level can be adjusted by changing the coupling condition between the microresonator and the through-port waveguide. A close-to-zero background can be achieved for the critical coupling condition. This way to tailor the pulse shape may be potentially useful for applications that require ultrashort bright pulses. The self-referenced cross-correlation is also measured to further verify the time-domain waveforms20, and the results are consistent with those reconstructed through spectral line-by-line shaping (see Figure 3e and 3f).
Time-domain characterization of the broadband mode-locked comb at stage III. (a, b) Amplitude and phase of the comb lines in the C-band. Although the amplitude of the pump line is very close at the through and drop ports, a clear phase difference can be observed. (c, d) Reconstructed waveforms at the through and drop ports, showing bright and dark pulses, respectively. Inst. freq.: instantaneous frequency. (e, f) Results of self-referenced cross-correlation, which are consistent with c and d.
Hot-cavity detuning measurement
The normal dispersion microring we investigate here is the same ring we used in our previous paper20. In that work, we showed that (i) the mode spectrum of the microring is perturbed by the avoided mode crossings induced by linear coupling between transverse modes and that (ii) the phase shifts associated with the linear coupling can enable comb generation, even in the normal dispersion regime, when pumping resonances around a mode-crossing region. This mechanism cannot, however, explain the comb generation described in the current paper. Indeed, a clear signature of the linear-mode coupling induced comb generation is that one of the initial comb sideband pairs always grows from the resonance which is shifted from its natural frequency due to mode coupling45, 46, 47. In contrast, here the laser pumps a resonance 4-FSR (~7 nm) away from the mode-crossing region; no frequency shifts due to mode coupling are observed for the resonances close to the pump from the cold-cavity dispersion profile, and no linear mode coupling induced comb lines are observed anywhere in the greater than one octave spectral measurement range. Of course, the mode-crossing position may slightly shift in a hot cavity when the microresonator is pumped because different transverse modes may have different thermal shifting rates20. Thus, to provide strong evidence that the comb generation we observe in Figure 2 is not due to linear mode coupling in the hot cavity, the relative positions of the resonances during comb operation with respect to the comb lines (that is, hot-cavity detuning) are measured.
The hot-cavity detuning can be measured using weakly modulated light23, 48, 49. In Ref 23, a probe laser passed through the cavity is used to measure the resonance transmission in the backward direction, and the relative position of the corresponding comb line can be resolved from its beat note with the probe laser. However, this method is not suitable for our setup due to the strong backward reflection of the comb power from the waveguide facet. Here, we use an improved method based on fiber comb spectroscopy. The setup is shown in Figure 4a. A fiber frequency comb with a 20 MHz repetition rate is injected into the microring from the drop port via a circulator. The power of the fiber comb is adjusted such that it does not introduce any observable thermal or Kerr shifting. The fiber comb lines passing through the microring are gathered via another circulator at the pump input port. Meanwhile, a fraction of the microcomb power is reflected to the backward direction from the waveguide facet and goes together with the fiber comb through the circulator (see the illustration in Figure 4a). The fiber comb and microcomb lines from the circulator are combined with a tunable reference laser, and their radiofrequency (RF) beat notes are detected with a photodetector and analyzed with an electrical spectrum analyzer. To measure a specified resonance and the corresponding microcomb line, the frequency of the reference laser is tuned ~10 GHz lower than that of the microcomb line. The fiber comb lines pick up the shape of the microring transmission spectrum and then beat with the reference laser. The relative resonant frequency is obtained by fitting the intensities of the fiber comb lines with a Lorentzian function, while the relative frequency location of the microcomb line is determined directly from its beat note with the reference laser. The hot-cavity detuning, defined as the resonance frequency minus the pump (or comb line) frequency, can then be calculated as the resonance RF beat frequency minus the microcomb line RF beat frequency. Two representative RF beat spectra indicating different detunings are shown in Figure 4b. The measurement accuracy of this method is estimated to be at the MHz level, which is much smaller than the resonance width (~200 MHz).
Hot-cavity detuning measurement. (a) Experimental setup. The frequency of the reference laser is ~10 GHz lower than the microcomb line to be measured. (b) Representative beat notes observed on the electrical spectrum analyzer. (c) Hot-cavity detuning, defined as the resonance frequency minus the microcomb frequency. A change in the linear slope can be observed when the comb transitions from stage II to stage III, indicating a jump in the comb line spacing. (d) Measured microcomb beat note with electro-optic down-mixing, showing the comb line spacing jump.
The measured hot-cavity detuning results are shown in Figure 4c. All the comb lines including the pump are always blue-detuned with respect to the resonances (that is, resonance frequency is lower than the frequency of pump or comb line). The detuning value is even larger than the resonance width. At stage III, the detuning versus wavelength is a quadratic function which indicates a normal group velocity dispersion of ~190 ps2 km−1, which is equal within experimental error to the dispersion measured for the cold cavity. The jump at ~1535 nm is due to linear transverse mode coupling. Note that no detuning jumps are observed for the two resonances adjacent to the pump at either stage II or stage III. This is consistent with our conclusion that the 1-FSR comb at stage II in Figure 2b is not due to linear mode coupling. At this point, we also note that the formation of the comb at stage II cannot be attributed to the usual MI induced by the cavity boundary conditions in normally dispersive cavities21, 22, 50, 51, 52: that instability only exists in a region that is not accessed when the pump laser is tuned from blue to red into the resonance27, 53, 54, as in our experiments. The comb formation dynamics are not completely analogous to those of self-induced MI lasers, either55, since the microresonator we use is a passive cavity without gain medium.
Another interesting feature is that the hot-cavity detuning at stage II shows a linear slope versus wavelength superimposed onto the same quadratic function from stage III, suggesting a mismatch between the comb line spacing and the cavity FSR. To further verify this behavior, the comb line spacing is measured using electro-optic down-mixing56, and the results are shown in Figure 4d. The comb line spacing is changed by 212.7 MHz from stage II to stage III, which agrees with the number retrieved from the detuning slope (214 MHz). Remarkably, all the key characteristics observed in the experiments, that is, the transition in the comb spectrum and the abrupt change in the comb line spacing, are accurately captured by the numerical simulations based on a theoretical model that includes the second-order nonlinear interactions between the fundamental and second-harmonic waves. In particular, these simulations unequivocally reveal that the comb formation is triggered by the fundamental−second-harmonic interactions. The details of these simulations will be shown in the next section.
Numerical simulation
As mentioned above, MI is absent from a microresonator with purely Kerr nonlinearity when the group velocity dispersion is normal and when the pump laser is tuned from blue to red into the resonance, as in our experiments27; thus, no comb generation should be observed. (Although linear-mode coupling may enable comb generation45, 46, 47, as we have explained above, our observations in the current experiment cannot be explained by this mechanism.) However, when there are simultaneous second- and third-order nonlinearities, a second-harmonic wave may be generated, with the fundamental and second-harmonic waves coupled to each other through the second-order nonlinearity. The evolution of the intracavity fields in this case follows coupled L–L equations (see equations (1) and (2) above) rather than the single L–L equation generally considered in Kerr comb generation. New dynamics may then arise that are responsible for the comb generation described in the current paper.
Figure 5 shows the simulation results based on equations (1) and (2), which are very similar to our experimental observations (see Supplementary Section 2.2 for simulation parameters and Supplementary Section 2.3 for a side-by-side plot of the experimental and simulation results). The thermo-optic effect is not considered in the simulation. With the pump laser continuously tuned into the resonance from the blue side, a narrow-band fundamental comb is generated and then transitions to a much broader spectrum, which corresponds to temporal dark pulse formation in the cavity. Detailed MI analyses (Supplementary Section 2.2) show that, due to the second-order nonlinear interactions, the frequency modes of the fundamental wave are coupled to those of the second-harmonic wave, resulting in an effect similar to linear transverse mode coupling. Specifically, in the simulation example shown in Figure 5, a close-to-phase-matching condition is achieved such that one comb sideband mode 1-FSR away from the pump is strongly coupled to its sum frequency with the pump through sum/difference frequency generation. The mode interaction gives rise to phase shifts that result in equivalent anomalous dispersion for the pump and the two adjacent fundamental modes. MI can thus occur, giving rise to the generation of a 1-FSR comb at stage II. The comb state becomes unstable in a small region right before transitioning to stage III, which is consistent with the experimental observation (see Supplementary Section 1). At this point, we emphasize that, as expected based on the strong normal dispersion, no modulation instability (or comb formation) is observed in our simulations when the second-order nonlinearity is neglected (κ=0). This further confirms that it is precisely the nonlinear mode coupling that permits comb generation for our parameters.
Numerical simulation based on coupled L–L equations. (a) Intracavity power versus detuning ( ). From top to bottom: total fundamental power, fundamental comb power excluding the pump and total second-harmonic power. (b) Spectra of the fundamental wave at different detuning stages marked in a. (c) Spectra of the second-harmonic wave. (d) Time-domain waveforms of the fundamental wave. Inst. freq.: instantaneous frequency. (e) Time-domain waveforms of the second-harmonic wave.
). From top to bottom: total fundamental power, fundamental comb power excluding the pump and total second-harmonic power. (b) Spectra of the fundamental wave at different detuning stages marked in a. (c) Spectra of the second-harmonic wave. (d) Time-domain waveforms of the fundamental wave. Inst. freq.: instantaneous frequency. (e) Time-domain waveforms of the second-harmonic wave.
The evolution of the fundamental intracavity waveform with the propagation distance is shown in Figure 6. Note that the waveform at stage II shows a time drift, which implies a deviation between the comb line spacing and the cavity FSR. The shifting rate is  fs per round-trip. The abrupt shift of the comb line spacing from stage II to stage III is then estimated as
fs per round-trip. The abrupt shift of the comb line spacing from stage II to stage III is then estimated as  , which is very close to the experimental result (212.7 MHz). The mismatch between the comb line spacing and the cavity FSR is caused by the second-harmonic mode coupling, which introduces additional phase shifts to the comb lines when the fundamental wave propagates in the cavity. The additional phase shifts effectively shift the resonances seen by the comb lines, resulting in an equivalent change of the local FSR. This effect is prominent at stage II (which achieves an effective anomalous dispersion for MI) and gets weaker at stage III due to the transition to the broader mode-locked comb state.
, which is very close to the experimental result (212.7 MHz). The mismatch between the comb line spacing and the cavity FSR is caused by the second-harmonic mode coupling, which introduces additional phase shifts to the comb lines when the fundamental wave propagates in the cavity. The additional phase shifts effectively shift the resonances seen by the comb lines, resulting in an equivalent change of the local FSR. This effect is prominent at stage II (which achieves an effective anomalous dispersion for MI) and gets weaker at stage III due to the transition to the broader mode-locked comb state.
Discussion
Very interestingly, MI and frequency comb generation in a cavity that contains a purely second-order nonlinear medium have been demonstrated recently29, 30, 57. It should be noted, however, that the mechanism for comb initiation in our paper is different from that in refs 29, 30 and 57. In particular, in our setup, the second-harmonic wave is relatively weak compared with the fundamental wave, such that the comb formation is still dominated by four-wave mixing due to the third-order Kerr effect. The role of the second-order nonlinearity is to induce phase shifts around the fundamental frequency (through second-harmonic mode coupling), which enables phase-matching for four-wave mixing. In this sense, the second-order nonlinearity can be regarded as a perturbation to the general single L–L equation. In the future, it would be highly interesting to pursue comb generation with much stronger second-order nonlinearity, as has been partially investigated in numerical simulations58.
Currently, the fundamental comb bandwidth we demonstrate is far less than one octave; thus, the external broadening of the comb spectrum will be required for comb self-referencing 59. Direct octave-spanning comb generation may be achieved by reducing the microresonator dispersion for the fundamental wave. Another highly interesting option is increasing the bandwidths of both the fundamental comb and the second-harmonic comb such that their spectra meet somewhere in the middle. This may allow new freedom in microresonator dispersion engineering.
Conclusions
In conclusion, we have showed that the interaction between the fundamental and the second-harmonic waves can provide a new way of phase matching for four-wave mixing in the normal dispersion region, under conditions where comb formation is prohibited in the absence of mode interaction. By employing this new mechanism, we have demonstrated second-harmonic-assisted mode-locked comb generation in an on-chip microresonator, which shows normal group velocity dispersion for the fundamental wave. A theoretical model incorporating coupled time-domain mean-field equations is developed, and numerical simulations unequivocally reveal the comb formation process triggered by the fundamental−second-harmonic interactions. Simultaneous comb formation and second-harmonic generation overcoming the dispersion limit would prove especially important in the near-visible to visible range, where several atomic transitions commonly used for the stabilization of optical clocks are located60 and where the strong normal material dispersion is likely to dominate. We expect that our findings will have a wide impact on the study of nonlinear cavity dynamics with interacting second-order and third-order nonlinearities.
Author contributions
XX led the experiments, with assistance from JAJ-V, P-HW and DEL. XX and YX designed the SiN microring layout. YX fabricated the microring. XX, FL and ME performed the theoretical analysis and did the numerical simulations. XX, FL, ME and AMW prepared the manuscript. The project was organized and coordinated by AMW and MQ.
References
Udem T, Holzwarth R, Hänsch TW . Optical frequency metrology. Nature 2002; 416: 233–237.
Del’Haye P, Schliesser A, Arcizet O, Wilken T, Holzwarth R et al. Optical frequency comb generation from a monolithic microresonator. Nature 2007; 450: 1214–1217.
Savchenkov AA, Matsko AB, Ilchenko VS, Solomatine I, Seidel D et al. Tunable optical frequency comb with a crystalline whispering gallery mode resonator. Phys Rev Lett 2008; 101: 093902.
Levy JS, Gondarenko A, Foster MA, Turner-Foster AC, Gaeta AL et al. CMOS-compatible multiple-wavelength oscillator for on-chip optical interconnects. Nat Photonics 2010; 4: 37–40.
Razzari L, Duchesne D, Ferrera M, Morandotti R, Chu S et al. CMOS-compatible integrated optical hyper-parametric oscillator. Nat Photonics 2010; 4: 41–45.
Grudinin IS, Baumgartel L, Yu N . Frequency comb from a microresonator with engineered spectrum. Opt Express 2012; 20: 6604–6609.
Jung H, Xiong C, Fong KY, Zhang XF, Tang HX . Optical frequency comb generation from aluminum nitride microring resonator. Opt Lett 2013; 38: 2810–2813.
Hausmann BJM, Bulu I, Venkataraman V, Deotare P, Lončar M . Diamond nonlinear photonics. Nat Photonics 2014; 8: 369–374.
Griffith AG, Lau RKW, Cardenas J, Okawachi Y, Mohanty A et al. Silicon-chip mid-infrared frequency comb generation. Nat Commun 2015; 6: 6299.
Kippenberg TJ, Holzwarth R, Diddams SA . Microresonator-based optical frequency combs. Science 2011; 332: 555–559.
Matsko AB, Liang W, Savchenkov AA, Maleki L . Chaotic dynamics of frequency combs generated with continuously pumped nonlinear microresonators. Opt Lett 2013; 38: 525–527.
Ferdous F, Miao HX, Leaird DE, Srinivasan K, Wang J et al. Spectral line-by-line pulse shaping of on-chip microresonator frequency combs. Nat Photonics 2011; 5: 770–776.
Papp SB, Diddams SA . Spectral and temporal characterization of a fused-quartz-microresonator optical frequency comb. Phys Rev A 2011; 84: 053833.
Herr T, Hartinger K, Riemensberger J, Wang CY, Gavartin E et al. Universal formation dynamics and noise of Kerr-frequency combs in microresonators. Nat Photonics 2012; 6: 480–487.
Saha K, Okawachi Y, Shim B, Levy JS, Salem R et al. Modelocking and femtosecond pulse generation in chip-based frequency combs. Opt Express 2013; 21: 1335–1343.
Del’Haye P, Beha K, Papp SB, Diddams SA . Self-injection locking and phase-locked states in microresonator-based optical frequency combs. Phys Rev Lett 2014; 112: 043905.
Huang SW, Zhou H, Yang J, McMillan JF, Matsko A et al. Mode-locked ultrashort pulse generation from on-chip normal dispersion microresonators. Phys Rev Lett 2015; 114: 053901.
Herr T, Brasch V, Jost JD, Wang CY, Kondratiev NM et al. Temporal solitons in optical microresonators. Nat Photonics 2014; 8: 145–152.
Yi X, Yang QF, Yang KY, Suh MG, Vahala K . Soliton frequency comb at microwave rates in a high-Q silica microresonator. Optica 2015; 2: 1078–1085.
Xue XX, Xuan Y, Liu Y, Wang PH, Chen S et al. Mode-locked dark pulse Kerr combs in normal-dispersion microresonators. Nat Photonics 2015; 9: 594–600.
Coillet A, Balakireva I, Henriet R, Saleh K, Larger L et al. Azimuthal Turing patterns, bright and dark cavity solitons in Kerr combs generated with whispering-gallery-mode resonators. IEEE Photonics J 2013; 5: 6100409.
Liang W, Savchenkov AA, Ilchenko VS, Eliyahu D, Seidel D et al. Generation of a coherent near-infrared Kerr frequency comb in a monolithic microresonator with normal GVD. Opt Lett 2014; 39: 2920–2923.
Del’Haye P, Coillet A, Loh W, Beha K, Papp SB et al. Phase steps and resonator detuning measurements in microresonator frequency combs. Nat Commun 2015; 6: 5668.
Brasch V, Geiselmann M, Herr T, Lihachev G, Pfeiffer MHP et al. Photonic chip–based optical frequency comb using soliton Cherenkov radiation. Science 2016; 351: 357–360.
Miller S, Luke K, Okawachi Y, Cardenas J, Gaeta AL et al. On-chip frequency comb generation at visible wavelengths via simultaneous second- and third-order optical nonlinearities. Opt Express 2014; 22: 26517–26525.
Jung H, Stoll R, Guo X, Fischer D, Tang HX . Green, red, and IR frequency comb line generation from single IR pump in AlN microring resonator. Optica 2014; 1: 396–399.
Haelterman M, Trillo S, Wabnitz S . Dissipative modulation instability in a nonlinear dispersive ring cavity. Opt Commun 1992; 91: 401–407.
Coen S, Randle HG, Sylvestre T, Erkintalo M . Modeling of octave-spanning Kerr frequency combs using a generalized mean-field Lugiato–Lefever model. Opt Lett 2013; 38: 37–39.
Leo F, Hansson T, Ricciardi I, De Rosa M, Coen S et al. Walk-off-induced modulation instability, temporal pattern formation, and frequency comb generation in cavity-enhanced second-harmonic generation. Phys Rev Lett 2016; 116: 033901.
Leo F, Hansson T, Ricciardi I, De Rosa M, Coen S et al. Frequency-comb formation in doubly resonant second-harmonic generation. Phys Rev A 2016; 93: 043831.
Lettieri S, Di Finizio S, Maddalena P, Ballarini V, Giorgis F . Second-harmonic generation in amorphous silicon nitride microcavities. Appl Phys Lett 2002; 81: 4706–4708.
Levy JS, Foster MA, Gaeta AL, Lipson M . Harmonic generation in silicon nitride ring resonators. Opt Express 2011; 19: 11415–11421.
Ning TY, Pietarinen H, Hyvärinen O, Simonen J, Genty G et al. Strong second-harmonic generation in silicon nitride films. Appl Phys Lett 2012; 100: 161902.
Ning TY, Pietarinen H, Hyvärinen O, Kumar R, Kaplas T et al. Efficient second-harmonic generation in silicon nitride resonant waveguide gratings. Opt Lett 2012; 37: 4269–4271.
Kitao A, Imakita K, Kawamura I, Fujii M . An investigation into second harmonic generation by Si-rich SiNx thin films deposited by RF sputtering over a wide range of Si concentrations. J Phys D Appl Phys 2014; 47: 215101.
Carmon T, Yang L, Vahala KJ . Dynamical thermal behavior and thermal self-stability of microcavities. Opt Express 2004; 12: 4742–4750.
Gorodetsky ML, Ilchenko VS . Thermal nonlinear effects in optical whispering-gallery microresonators. Laser Phys 1992; 2: 1004–1009.
Fomin AE, Gorodetsky ML, Grudinin IS, Ilchenko VS . Nonstationary nonlinear effects in optical microspheres. J Opt Soc Am B 2005; 22: 459–465.
Johnson TJ, Borselli M, Painter O . Self-induced optical modulation of the transmission through a high-Q silicon microdisk resonator. Opt Express 2006; 14: 817–831.
He LN, Xiao YF, Zhu JG, Ozdemir SK, Yang L . Oscillatory thermal dynamics in high-Q PDMS-coated silica toroidal microresonators. Opt Express 2009; 17: 9571–9581.
Baker C, Stapfner S, Parrain D, Ducci D, Leo G et al. Optical instability and self-pulsing in silicon nitride whispering gallery resonators. Opt Express 2012; 20: 29076–29089.
Zhang LB, Fei YH, Cao YM, Lei X, Chen SW . Experimental observations of thermo-optical bistability and self-pulsation in silicon microring resonators. J Opt Soc Am B 2014; 31: 201–206.
Xue XX, Xuan Y, Wang C, Wang PH, Liu Y et al. Thermal tuning of Kerr frequency combs in silicon nitride microring resonators. Opt Express 2016; 24: 687–698.
Weiner AM . Ultrafast Optics. Wiley: Hoboken, NJ, USA; 2009.
Savchenkov AA, Matsko AB, Liang W, Ilchenko VS, Seidel D et al. Kerr frequency comb generation in overmoded resonators. Opt Express 2012; 20: 27290–27298.
Liu Y, Xuan Y, Xue XX, Wang PH, Chen S et al. Investigation of mode coupling in normal-dispersion silicon nitride microresonators for Kerr frequency comb generation. Optica 2014; 1: 137–144.
Xue XX, Xuan Y, Wang PH, Liu Y, Leaird DE et al. Normal-dispersion microcombs enabled by controllable mode interactions. Laser Photonics Rev 2015; 9: L23–L28.
Matsko AB, Maleki L . Feshbach resonances in Kerr frequency combs. Phys Rev A 2015; 91: 013831.
Matsko AB, Maleki L . Noise conversion in Kerr comb RF photonic oscillators. J Opt Soc Am B 2015; 32: 232–240.
Coen S, Haelterman M . Modulational instability induced by cavity boundary conditions in a normally dispersive optical fiber. Phys Rev Lett 1997; 79: 4139–4142.
Coen S, Haelterman M, Emplit P, Delage L, Simohamed LM et al. Bistable switching induced by modulational instability in a normally dispersive all-fibre ring cavity. J Opt B: Quantum Semiclass Opt 1999; 1: 36–42.
Savchenkov AA, Rubiola1 E, Matsko AB, Ilchenko VS, Maleki L . Phase noise of whispering gallery photonic hyper-parametric microwave oscillators. Opt Express 2008; 16: 4130–4144.
Hansson T, Modotto D, Wabnitz S . Dynamics of the modulational instability in microresonator frequency combs. Phys Rev A 2013; 88: 023819.
Godey C, Balakireva IV, Coillet A, Chembo YK . Stability analysis of the spatiotemporal Lugiato-Lefever model for Kerr optical frequency combs in the anomalous and normal dispersion regimes. Phys Rev A 2014; 89: 063814.
Sylvestre T, Coen S, Emplit P, Haelterman M . Self-induced modulational instability laser revisited: normal dispersion and dark-pulse train generation. Opt Lett 2002; 27: 482–484.
Del’Haye P, Papp SB, Diddams SA . Hybrid electro-optically modulated microcombs. Phys Rev Lett 2012; 109: 263901.
Ricciardi I, Mosca S, Parisi M, Maddaloni P, Santamaria L et al. Frequency comb generation in quadratic nonlinear media. Phys Rev A 2015; 91: 063839.
Hansson T, Leo F, Erkintalo M, Anthony J, Coen S et al. Single envelope equation modeling of multi-octave comb arrays in microresonators with quadratic and cubic nonlinearities. J Opt Soc Am B 2016; 33: 1207–1215.
Del'Haye P, Coillet A, Fortier T, Beha K, Cole DC et al. Phase-coherent microwave-to-optical link with a self-referenced microcomb. Nat Photonics 2016; 10: 516–520.
Ludlow AD, Boyd MM, Ye J, Peik E, Schmidt PO . Optical atomic clocks. Rev Mod Phys 2015; 87: 637–701.
Acknowledgements
This work was supported in part by the National Science Foundation under grant ECCS-1509578, by the Air Force Office of Scientific Research under grant FA9550-15-1-0211, and by the DARPA PULSE program through grant W31P40-13-1-0018 from AMRDEC. XX acknowledges funding from the National Natural Science Foundation of China under grant 6169190011/12, 61420106003, and the Beijing Natural Science Foundation under grant 4172029. ME acknowledges funding from the Marsden Fund and the Rutherford Discovery Fellowships of the Royal Society of New Zealand.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Xue, X., Leo, F., Xuan, Y. et al. Second-harmonic-assisted four-wave mixing in chip-based microresonator frequency comb generation. Light Sci Appl 6, e16253 (2017). https://doi.org/10.1038/lsa.2016.253
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2016.253
Keywords
This article is cited by
-
Optical properties and applications of metal nanomaterials in ultrafast photonics: a review
Journal of Materials Science (2024)
-
Modeling of dual frequency combs and bistable solitons in third-harmonic generation
Communications Physics (2023)
-
Optically reconfigurable quasi-phase-matching in silicon nitride microresonators
Nature Photonics (2022)
-
Efficient photoinduced second-harmonic generation in silicon nitride photonics
Nature Photonics (2021)
-
Dual-resonance enhanced quantum light-matter interactions in deterministically coupled quantum-dot-micropillars
Light: Science & Applications (2021)