Abstract
Efficient nonlinear conversion requires that interacting optical waves maintain a consistent phase relationship when traveling in a medium despite its dispersion. Birefringent phase-matching, which is often used to compensate for the dispersion, is not applicable to optically isotropic nonlinear materials. Here, we present a one-dimensional photonic crystal structure that allows the propagation of optical surface waves, both at the fundamental and third-harmonic frequencies, as an efficient medium for phase-matched third-harmonic generation. A unique advantage of this structure is that the effective refractive indices for the surface waves are similar to the refractive index of air at both frequencies. This allows phase-matching between the first and third harmonics, and a visible collinear beam of the third harmonic is produced at the prism-coupled output. Moreover, these optical surface waves propagate over long distances even if a lossy nonlinear nanofilm is deposited onto the photonic crystal surface. We provide experimental results for third-harmonic generation at a wavelength of 410 nm for a bare dielectric Ta2O5/SiO2 multilayer structure and for the same structure coated with a 15-nm GaAs film.
Similar content being viewed by others
Introduction
Nonlinear photonic devices, particularly those that can be fabricated by planar processing technology, show great promise for future all-optical signal processing. In configurations that perform efficient nonlinear conversion, large nonlinear susceptibilities are crucial for application to such photonic technologies. The nonlinear optical susceptibility of a material can be defined by expanding its polarization as a power series in terms of the applied optical electric field E:

where, χ(1) is the linear susceptibility; the second-order susceptibility χ(2) describes processes, such as second-harmonic generation; and the third-order susceptibility χ(3) describes, for example, third-harmonic generation (THG) and the intensity-dependent addition to the refractive index n2·I (with the nonlinear refractive index n2=12π2χ(3)/n02)1. The coefficient χ(2) is non-zero only in non-centrosymmetric materials, whereas χ(3) is non-zero in all optical materials, regardless of their symmetry.
However, even though χ(3) is non-vanishing in all media, its small value makes the implementation of third-order non-linearity in integrated planar photonic devices a formidable challenge. One approach to increase χ(3) in planar systems is based on the hybrid (organic-semiconductor) structures2. It was shown that a substantial enhancement of χ(3) could be achieved both in strongly coupled hybrid structures3 and in hybrid structures with weak coupling4.
In addition to enhanced nonlinear susceptibilities, an intelligent design of planar configurations that provide phase-matching of interacting optical waves is crucial for experimental development of these hybrid structures.
THG is a straightforward manifestation of third-order non-linearity. However, in this case, phase-matching is difficult or impossible to realize because of the large interval between the wavelengths.
Here, we demonstrate THG in a planar multilayer structure where the effective refractive index (RI) for each surface wave (the first and third harmonics) is very close to that of air (nair≃1) and the phases of the interacting waves match. This one-dimensional (1D) photonic crystal (PC) structure can accommodate further semiconductor and organic nanolayers deposited on its external surface, which makes such a system ideal for investigating different planar hybrid schemes with enhanced χ(3).
It is important that the proposed 1D design is easy to produce and is compatible with the planar processing technology. In recent years, several high-efficiency THG schemes have been proposed, based on, for example, 3D PC5, 2D photonic waveguides6 or nano-sized silicon-based plasmonic waveguides7. However, these approaches require nanofabrication facilities, whereas the planar design presented here can be achieved using standard multilayer-coating equipment.
Materials and methods
PC structures
PCs are materials that possess a periodic modulation of their refraction indices on the scale of the light wavelength8. Such materials can exhibit photonic band gaps that are very much like the electronic band gaps for the electron waves traveling in the periodic potential of the crystal. In both cases, frequency intervals exist in which wave propagation is forbidden. This analogy may be extended9 to include surface levels that can exist in the band gaps of electronic crystals. In PCs, these correspond to optical surface waves with dispersion curves located inside the photonic band gap. These PC surface waves (PC SWs), which are sometimes also called ‘photonic band-gap surface modes’, ‘modes of (asymmetric) planar Bragg waveguide’, ‘surface waves in periodic layered medium’, ‘optical Bloch surface waves’ or ‘surface waves in multilayer coating’, were studied in the 1970s, both theoretically10, 11 and experimentally12. Twenty years later, the excitation of optical SWs in a Kretschmann-like configuration was demonstrated13. Recently, PC SWs have found applications in growing fields, such as optical biosensors14, 15, 16 and surface-enhanced Raman scattering17.
Our 1D PC had the following structure: substrate/H(LH)14 L′/air, where L represents a SiO2 layer (thickness d1=321.7 nm), H is a Ta2O5 layer (d2=146.7 nm) and L′ is a SiO2 layer (d3=211.7 nm). This structure was also used with an additional GaAs coating (thickness 15 nm) applied to the 1D PC surface.
Film deposition
The Ta2O5/SiO2 multilayer was deposited by magnetron sputtering. An additional GaAs nanofilm was applied by metal organic chemical vapor deposition. The prism and substrate were made from fused silica. The RI values of the prism, SiO2, Ta2O5 layers and air at λ=1230 nm are n0=n1=n3=nSiO2=1.45, n2=nTa2O5=2.02 and nair=1.0003, respectively (see Figure 1). The RI values at other wavelengths were derived using the dispersion data given by Palik18.
Laser sources
Two different laser sources were used in the experiments for pico and femtosecond pulses. Picosecond infrared radiation at the wavelength of 1230 nm with a pulse duration of 3 ps was generated by an optical parametric oscillator (MIRA-OPO, APE GmbH, Berlin, Germany) that was pumped synchronously by a picosecond mode-locked Ti:Sapphire laser (MIRA 900D, Coherent, Santa Clara, CA, USA) at a repetition rate of 76.4 MHz. To ensure the stability of infrared radiation power during the experiment, the OPO cavity length was actively stabilized. Femtosecond pulses at 1230 nm were generated by a parametric amplifier (Topas, Light Conversion Ltd., Vilnius, Lithuania) pumped by a Ti:sapphire regenerative amplifier (Spitfire Pro, Spectra Physics, Newport Corp., Irvine, CA, USA) at a repetition rate of 1 kHz. Signal (1230 nm) and idler (2330 nm) beams were separated by a specialized wavelength separator (Light Conversion Ltd.). Then, the signal beam was guided through an achromatic half-wave plate and a variable continuous neutral-density filter (both from Thorlabs, Newton, NJ, USA) to prepare p-polarized 1 μJ, 100 fs, 1230-nm pulses incident on the prism.
Detectors
The picosecond signals generated near 410 nm were detected using a back-illuminated EMCCD camera (Andor iXon3 897, Belfast, UK) that was thermoelectrically cooled to −100 °C. A standard camera lens of 50 mm focal length formed the image on a 512 × 512 format matrix with the pixel size of 16 μm. Femtosecond excitation produced a directional emission of blue light that was visible by the naked eye. The spectrum of this emission was registered using a grating CCD spectrometer with a fiber-optic input (ASP-100MF, Avesta Ltd., Moscow, Russia).
Results and discussion
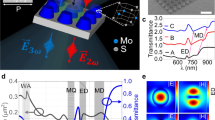
The experimental setup is outlined in Figure 1. A laser beam with a wavelength λ1=1230 nm excites PC SWs on the external surface of a Ta2O5/SiO2 multilayer structure. The confinement of the PC surface wave (SW) field near the interface arises from the photonic band gap in the multilayer structure on one side of the external surface and from total internal reflection (TIR) on the other side of the external surface. TIR requires that the effective RI for a PC SW exceeds the RI of the external medium. The effective RI (or, equivalently, the wave vector) of the incoming light can be increased in several ways, for example, via grating coupling or end-fire coupling. In this work, we used a Kretschmann-like scheme to excite PC SWs through a prism in the range of angles displaying TIR.
The 1D PC structure is designed so that both the fundamental and third-harmonic wavelengths are within the photonic band gaps, where the PC SWs are located. Figure 2 shows the calculated dispersion of the structure together with measurements of the PC SW excitation. Clearly, both dispersion curves approach the light line (ρ=nair). In contrast to most optical materials, the RI of air is almost wavelength-independent, so that an angular range exists near the TIR threshold where ρSW1=ρSW3, indicating phase matching between the first and third harmonics. In this structure, such phase matching occurs at ρ≃1.04, as shown in Figure 2 by the black-and-white pentagrams.
Calculated and measured dispersions of the 1D PC structure. The dispersion is presented as the logarithm of the optical-field enhancement factor (that is, log10 (Ie/I0)) in the external medium near the structure. A general view of the dispersion (b) is shown in the coordinates 1/λ(ρ), whereas a more detailed view of the first- (c) and third-harmonic (a) band gaps is shown in the coordinates λ(ρ). The photonic band gaps are clearly apparent as the dark blue regions with an enhancement much less than 1. The optical surface mode is shown as the red curves with an enhancement of ~100 inside the band gaps. The measured points for the PC SW excitation at different wavelengths and angles are shown for the first (c, cyan squares) and third harmonics (a, magenta diamonds). An angular parameter ρ=n0sin(θ0), at which the excitation of the surface mode occurs, is equal to the effective RI of the mode.
This phase-matching strategy should be distinguished from the one developed by Helmy et al 19, 20. for second-harmonic generation, where phase matching occurs between the fundamental mode of a conventional waveguide (with TIR on both interfaces) and the second-harmonic mode of a PC waveguide. Indeed, in our case, both interacting modes are PC SW modes located in band gaps of different orders, and both have effective indices close to the RI of air.
The third-harmonic intensity was markedly enhanced when the angle (Figure 3a) and wavelength (Figure 3b) of the picosecond-laser excitation beam approached this phase-matching point. To illustrate this situation, the dispersion of the third harmonics and the frequency-shifted (λ1/3) dispersion of the first harmonics are superimposed in Figure 3c. The measurements (λ, ρ) for the PC SW excitation for both infrared and visible dispersion curves (the same as in Figure 2a and 2c) are also displayed together (cyan squares and magenta diamonds for the first and third harmonics, respectively).
THG intensity near the phase-matching point. (a) Angular and (b) wavelength dependences of P3rd—average power of the third harmonic. Solid lines represent a fit of the measured data. (c) Measurements and contour plot of the PC SW’s dispersion, superimposed by frequency-shifting. Left-hand y-axis is for the third-harmonic dispersion curves, whereas right-hand y-axis is for the first-harmonic data. The angular and wavelength ranges from a and b plots are shown in c as red and cyan solid lines, respectively.
On the basis of the results in Figure 3, we conclude that the observed third-harmonic enhancement in our 1D PC results from phase matching. To verify that the observed signal is generated by a nonlinear process involving χ(3), we also measured the dependence of THG on the picosecond pump pulse energy, with the results shown in the log–log plot in Figure 4. The slope of the linear fit equals 3.1±0.3, confirming third-order non-linearity.
The above measurements were performed using picosecond-laser excitation, whereas the third-harmonic radiation was detected with a CCD camera. Femtosecond laser excitation makes blue-light emission visible with the naked eye. The produced blue light beam is highly directional with a natural divergence of 4 × 10−3 rad. This directional blue beam appears on the exit side of the coupled prism at an angle that is slightly different from that of the first harmonic, as shown schematically in Figure 1. This difference in angles is due to the fact that n0(λ3)>n0(λ1), and therefore, θ(λ3)<θ(λ1) at the phase-matching point where ρ(λ3)=ρ(λ1). Both spots (the fundamental and third-harmonic beams) are clearly visible on an IR visualizer, and their angular separation in air can be measured. The measured angle (Δθ=1.370) is very close to the expected value deduced from the quartz prism dispersion.
In addition to field enhancement and phase matching, the presented 1D PC structure has another unique property: it supports long-range propagation of the PC SWs even if the surface is coated with a nanofilm made of strongly absorbing material. This ultra-long-range propagation was predicted and experimentally confirmed for a metal-coated 1D PC when the effective RI of the optical surface mode is very close to the RI of the external media (for example, air)21. The effect was confirmed not only for the nanofilms made from ‘plasmonic metals’ (for example, gold) but also for the nanofilms made from very lossy materials (for example, palladium)22.
The usefulness of this feature for the development of nonlinear devices is obvious. Indeed, many nonlinear materials with a large χ(3) are also very lossy, limiting nonlinear interactions. For example, some semiconductors, such as Si and GaAs, have a very large χ(3) (an order of magnitude greater than LiNbO3), but their RI also has a large imaginary part, especially for the third-harmonic that is usually produced in the spectral region of the intrinsic absorption of a semiconductor. To demonstrate this feature, we deposited a 15-nm-thick GaAs nanofilm on the external side of our multilayer structure.
Table 1 lists the nonlinear coefficients of the materials constituting our 1D PC23, 24, 25. Clearly, in the absence of the GaAs nanofilm, Ta2O5 is a major contributor to THG, with χ(3) that is an order of magnitude greater than that for SiO2. GaAs has a cubic structure and therefore is an optically isotropic material. In contrast to birefringent nonlinear crystals, frequency conversion in isotropic materials is limited by the difficulty of achieving phase matching, so that more complicated schemes of quasi-phase-matching are used in GaAs26.
In addition, the GaAs band gap is 1.42 eV; thus, strong intrinsic absorption occurs for wavelengths shorter than 870 nm. In our structure, the deposition of a 15-nm-thick GaAs nanofilm further increases the THG intensity and shifts the wavelength of the third-harmonic slightly by +1.6 nm (see Figure 5). A small additional spectral feature near 430 nm is THG at the photonic band-gap edge that is excited by femtosecond pulses of wide bandwidth (1230±25 nm). An image of the third-harmonic beam is shown in the inset of Figure 5. These spectra were recorded using femtosecond excitation at 1230 nm with an average beam power of 1 mW and a repetition rate of 1 kHz. The fundamental wave was weakly focused by a lens with a focal distance of 300 mm.
The THG conversion efficiency in our system is estimated to be 4 × 10−27 (cm2 W−1)2. As an example, for the average pump power of 1 mW and the focal spot area of 2.8 × 10−4 cm2 (corresponding to pulse peak intensity of 3.6 × 1010 W cm−2), the conversion efficiency is 5 × 10−6, and we obtain 5 nW of third-harmonic radiation produced at 411.6 nm. The maximum pulse peak intensity in our experiments is 1.9 × 1011 W cm−2 (at the average pump power of 70 mW and spot size of 3.6 × 10−3 cm2), giving the conversion efficiency of 1.5 × 10−4 and 11 μW of third-harmonic radiation. THG efficiency can be further increased by optimizing the 1D PC structure to accommodate the full bandwidth of the femtosecond pulses, improving the composition of the GaAs nanofilms, and creating resonant hybrid (semiconductor-organic) structures on the surface.
Conclusion
We demonstrated THG in a single step via optical surface modes on a 1D PC when both the fundamental and third-harmonic frequencies resonate with the corresponding surface modes. Three key properties of the 1D PC structure increase the otherwise poor efficiency of THG:
-
i
Localization and enhancement of the optical field near the surface via PC SW excitation;
-
ii
Phase-matching between the first- and the third-harmonic SWs, both of which have an effective RI close to that of the almost dispersionless air;
-
iii
Long-range propagation of surface waves in a nonlinear nanofilm deposited onto the 1D PC, even if considerable optical losses are present at the third-harmonic frequency for this material.
References
Boyd RW . Nonlinear Optics. San Diego: Academic Press; 1992.
Agranovich VM, Gartstein YN, Litinskaya M . Hybrid resonant organic-inorganic nanostructures for optoelectronic applications. Chem Rev 2011; 111: 5179–5214.
Agranovich VM, Basko DM, La Rocca GC, Bassani F . Excitons and optical nonlinearities in hybrid organic-inorganic nanostructures. J Phys Condens Matter 1998; 10: 9369–9400.
Agranovich VM, La Rocca GC . Organic-inorganic heterostructures for nonlinear optics. J Lumin 2016; 169: 422–425.
Markowicz PP, Tiryaki H, Pudavar H, Prasad PN, Lepeshkin NN et al. Dramatic enhancement of third-harmonic generation in three-dimensional photonic crystals. Phys Rev Lett 2004; 92: 083903.
Corcoran B, Monat C, Grillet C, Moss DJ, Eggleton BJ et al. Green light emission in silicon through slow-light enhanced third-harmonic generation in photonic-crystal waveguides. Nat Photonics 2009; 3: 206–210.
Sederberg S, Elezzabi AY . Coherent visible-light-generation enhancement in silicon-based nanoplasmonic waveguides via third-harmonic conversion. Phys Rev Lett 2015; 114: 227401.
Yablonovitch E . Photonic band-gap structures. J Opt Soc Am B 1993; 10: 283–295.
Kossel D . Analogies between thin-film optics and electron band theory of solids. J Opt Soc Am 1966; 56: 1434.
Arnaud JA, Saleh AAM . Guidance of surface waves by multilayer coatings. Appl Opt 1974; 13: 2343–2345.
Yeh P, Yariv A, Hong CS . Electromagnetic propagation in periodic stratified media. I. General theory. J Opt Soc Am 1977; 67: 423–438.
Yeh P, Yariv A, Cho AY . Optical surface waves in periodic layered media. Appl Phys Lett 1978; 32: 104–105.
Robertson WM, May MS . Surface electromagnetic waves on one-dimensional photonic band gap arrays. Appl Phys Lett 1999; 74: 1800–1802.
Shinn A, Robertson W . Surface plasmon-like sensor based on surface electromagnetic waves in a photonic band-gap material. Sens Actuator B Chem 2005; 105: 360–364.
Konopsky VN, Alieva EV . Photonic crystal surface waves for optical biosensors. Anal Chem 2007; 79: 4729–4735.
Konopsky VN, Karakouz T, Alieva EV, Vicario C, Sekatskii SK et al. Photonic crystal biosensor based on optical surface waves. Sensors 2013; 13: 2566–2578.
Pirotta S, Xu XG, Delfan A, Mysore S, Maiti S et al. Surface-enhanced Raman scattering in purely dielectric structures via Bloch surface waves. J Phys Chem C 2013; 117: 6821–6825.
Palik ED . Handbook of Optical Constants of Solids. London: Academic Press; 1985.
Helmy AS . Phase matching using Bragg reflection waveguides for monolithic nonlinear optics applications. Opt Express 2006; 14: 1243–1252.
Arjmand A, Abolghasem P, Han JB, Helmy AS . Interface modes for monolithic nonlinear photonics. J Opt Soc Am B 2015; 32: 577–587.
Konopsky VN, Alieva EV . Long-range propagation of plasmon polaritons in a thin metal film on a one-dimensional photonic crystal surface. Phys Rev Lett 2006; 97: 253904.
Konopsky VN, Alieva EV . Long-range plasmons in lossy metal films on photonic crystal surfaces. Opt Lett 2009; 34: 479–481.
Boyd R, Fischer G Nonlinear optical materials. In: Buschow KHJ, Cahn RW, Flemings MC, Ilschner B, Kramer EJ et al eds. Encyclopedia of Materials: Science and Technology, 2nd edn. Oxford: Elsevier; 2001, p6237–6244.
Hashimoto T, Yoko T . Third-order nonlinear optical properties of sol-gel-derived V2O5, Nb2O5, and Ta2O5 thin films. Appl Opt 1995; 34: 2941–2948.
Tai CY, Wilkinson JS, Perney NMB, Netti MC, Cattaneo F et al. Determination of nonlinear refractive index in a Ta2O5 rib waveguide using self-phase modulation. Opt Express 2004; 12: 5110–5116.
Kuo PS, Bravo-Abad J, Solomon GS . Second-harmonic generation using 4-quasi-phasematching in a GaAs whispering-gallery-mode microcavity. Nat Commun 2014; 5: 3109.
Acknowledgements
This study was supported by the Russian Foundation for Basic Research, research project No. 14-29-07132 and partially by research project No. 14-29-07197. We thank AA Padalitsa for the preparation of the 15-nm GaAs nanofilms. Sergey Alyatkin acknowledges EUV Labs for financial support of his work and for providing the picosecond laser system and the CCD camera for doing experiment.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
N Konopsky, V., V Alieva, E., Yu Alyatkin, S. et al. Phase-matched third-harmonic generation via doubly resonant optical surface modes in 1D photonic crystals. Light Sci Appl 5, e16168 (2016). https://doi.org/10.1038/lsa.2016.168
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2016.168
Keywords
This article is cited by
-
An excellent deep-ultraviolet birefringent material based on [BO2]∞ infinite chains
Light: Science & Applications (2022)
-
Electrical Excitation of Long-Range Surface Plasmons in PC/OLED Structure with Two Metal Nanolayers
Nano-Micro Letters (2020)
-
Coherent power amplification of third-order harmonic femtosecond pulses at thin-film up-conversion nanoparticles
Scientific Reports (2019)