Abstract
Quantum secure direct communication is an important mode of quantum communication in which secret messages are securely communicated directly over a quantum channel. Quantum secure direct communication is also a basic cryptographic primitive for constructing other quantum communication tasks, such as quantum authentication and quantum dialog. Here, we report the first experimental demonstration of quantum secure direct communication based on the DL04 protocol and equipped with single-photon frequency coding that explicitly demonstrated block transmission. In our experiment, we provided 16 different frequency channels, equivalent to a nibble of four-bit binary numbers for direct information transmission. The experiment firmly demonstrated the feasibility of quantum secure direct communication in the presence of noise and loss.
Similar content being viewed by others
Introduction
Secure communication is not only vital in military use and national security, but also important in modern everyday life. Quantum communication provides a novel way of communication with unconditional security. The fundamental difference between quantum communication and classical communication is on the capability to detect eavesdropping on-site. There are different modes of quantum communication: quantum key distribution (QKD)1, quantum secret sharing2, quantum secure direct communication (QSDC)3, quantum teleportation4 and quantum dense coding5.
Since the earliest BB84 protocol was proposed1, QKD has been researched extensively, and the application over a distance of a few hundreds of kilometers has been achieved6. QKD can be completed non-deterministically, for instance, in the BB84 and BBM92 protocols1, 7, where the key is distributed indeterminately. Alternatively, deterministic QKD communication8, 9, 10, 11, 12, 13 is essentially a deterministic QKD process plus a classical communication. Alice first chooses a random key and uses it to encrypt the secret message into ciphertext, and then transmits the ciphertext to Bob through a quantum channel. If both of them are certain that no eavesdroppers exist, Alice sends the key to Bob through a classical channel.
In contrast to QKD communication, QSDC sends secret information securely through a quantum channel directly without setting up a prior key3, 14, 15. Since the first QSDC protocol was proposed3, it has become one of the hot research topics in quantum communication over the past decade. The secure direct nature of QSDC also makes it an important cryptographic primitive. Protocols of quantum signature16, quantum dialog17, 18 and quantum direct secret sharing19, 20 were all constructed on the basis of QSDC. The security of QSDC relies on quantum principles, such as the no-cloning theorem, the uncertainty principle, correlation of entangled particles and nonlocality. In addition, QSDC has been enhanced by a block transmission technique that was proposed in the first QSDC protocol by Long and Liu3. For entanglement carriers, in 2003, Deng et al.21 proposed a two-step QSDC protocol where the criteria for QSDC were explicitly stated. QSDC protocols based on high-dimensional entanglement22, 23, 24, multipartite entanglement25, 26, 27 and hyperentanglement28 were developed one by one. For single photons carriers, the first QSDC protocol was proposed in Ref. 29, the so-called DL04 protocol, wherein, the information was directly encoded in the single photons. Here, 0 is encoded with I=|0〉〈0|+|1〉〈1| and 1 with U=iσy=|0〉〈1|−|1〉〈0|. High-capacity QSDC protocols were proposed with single photons carriers30, which can carry 2 bits of information with a single photon, as the sender encodes the message in both the polarization state and the spatial-mode state, independently.
However, the channel loss of the photons would lead to the loss of the secret information when it is encoded in the individual photons. When there is noise in the quantum channel, an adversary Eve can gain a certain amount of information by hiding her presence in the channel noise. In this case, the information leakage may be eliminated by using either quantum error correction31 or quantum privacy amplification32. Unfortunately, quantum privacy amplification ruins the direct communication picture because it involves merger and order reshuffling of single photons. An efficient way to implement QSDC in a noisy channel is to use quantum error correction31, 33. Post-processing can be performed using quantum error correction without using privacy amplification and reconciliation34. In this work, instead of using the complicated quantum error correction, we present a new QSDC protocol on the basis of a single-photon frequency coding scheme, called the FRECO-DL04 protocol. The information is encoded in the frequency spectrum of a block of single photons rather than on the individual photons. It is experimentally shown that FRECO-DL04 can work efficiently in the presence of channel loss and noise.
Materials and methods
FRECO-DL04 protocol
Suppose that Bob wants to send secret information to Alice. The protocol contains the following four steps:
-
1)
Alice prepares a block of N2 single photons. Each photon in the block is randomly in one of four states: |0〉, |1〉, |+〉 and |−〉, where |0〉 and |1〉 are the eigenstates of the Pauli Z operator, and |±〉=(|0〉±|1〉)/√2 are the eigenstates of the Pauli X operator. Then, Alice sends the single-photon block to Bob, and Bob acknowledges this fact.
-
2)
Because of channel noise and loss, Bob receives only N1 single photons (N1<N2). He selects CN1 number (C is a positive number less than or equal to 1/2) of photons randomly from the N1 received photons for eavesdropping check by measuring them randomly in the X-basis or the Z-basis (control mode29). Then, Bob tells Alice the positions, the measuring-basis and the measuring results of these measured photons. Alice compares her results with those of Bob and obtains an error rate. If the error rate is higher than the threshold, they abort the communication. If the error rate is less than the threshold, the Alice-to-Bob communication is considered safe and continues to step 3.
-
3)
The remaining (1−C)N1 received photons are used for encoding the secret information (Encode mode). Bob also selects C(1−C)N1 single photons from the remaining photons randomly as check bits for the Bob-to-Alice transmission and randomly applies one of the two operations, U=iσy=|0〉〈1|−|1〉〈0| and I=|0〉〈0|+|1〉〈1|, which flips or does not flip the state of the photon. The rest of the single photons are processed by the single-photon frequency coding scheme, which are described below.
-
4)
Bob sends the encoded photon block back to Alice who can deterministically decode Bob’s operations by measuring the photons in the same basis as she prepared them. Alice obtains the operation of each single photon in the block and their arrival time. Because of channel loss, Bob receives only N (here N≤(1−C)2N1) photons in each block after subtracting the check photons. Alice and Bob also publicly compare the results of the checking bits to check for eavesdropping in the Bob-to-Alice transmission. Next, Alice analyzes the frequency spectrum and determines Bob’s encoded bits and retrieves the secret information.
Single-photon frequency coding
In the DL04 protocol, the information is directly encoded in the individual photons, where 0 is encoded with operation I and 1 with U. The operation U flips the state without changing the measurement basis, namely

Instead of using an individual operation to encode a bit value, single-photon frequency coding applies a series of operations periodically on a single-photon block to encode information. Bob applies the operations U and I on single photons in the block according to a periodic function with period T=1/f, where f is the modulation frequency that encodes the information. Typically, different modulation frequencies correspond to the different binary bit sequences. Once Alice obtains the modulation frequencies spectrum after she measures a block of single photons, she gets Bob's information fully. The encoding operation Bob applies to the single-photon block, after excluding the checking bits, is

where δ is the initial phase of each modulation signal, which could be an arbitrary value between 0 and 2π, and f is the modulation frequency. An example is given in Table 1, where the initial states, the final states, the measured operations x(i) and arrival times τi are shown. The measured values x(i) that Alice obtained denote Bob’s flip U (denoted as 1) or no flip I (denoted as 0) operations. Alice records the arrival time τi, for i=1, 2, 3,…, N, where N is the number of single photons that she has measured in each block after subtracting the check photons.
Not all the photons can arrive at Alice’s side because of the loss of optical fiber and imperfect detection efficiency of the single-photon detector. However, this single-photon frequency coding scheme is robust against loss and error. The information is encoded in the frequency spectrum of the single-photon block, instead of individual photons, where the loss and error of some photons would change only the signal-to-noise ratio (SNR) of the frequency spectrum. The modulation frequency can be accurately determined from the block (x(i), τi) using the discrete time Fourier transform,

From the frequency spectrum line at the modulation frequency, Alice can determine the encoded frequency and reads out the secret information.
For a given quantum communication system, there exists a finite maximum number Nc of frequency channels,

where fmax and fmin are the maximum and minimum modulation frequencies, respectively, and fb is the channel spacing. The information transmission capacity relies on the number of frequency components. Assuming Bob loads r frequency components on one single-photon block, the effective degrees of freedom are the total number of different combinations of r frequencies over the Nc frequency channels,

which means one single-photon block can carry b=log2Nmax bits of information. The transmission rate can be expressed as

where Tspan is the time span, that is, the time length of a single-photon block. The principle of the coding scheme is similar to the ultra-wide-band communication in the field of wireless communication35.
Experimental setup
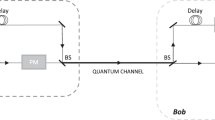
The experimental setup is shown in Figure 1. A strong attenuated laser (1550 nm, NP Photonics RELS) was used as a single-photon source with systematic pulse repetition frequency of 10 MHz. Alice sends the single-photon block to Bob. The QSDC operation system is controlled by a field programmable gate array (FPGA) device. The control mode, as shown in Figure 1, is used to check for eavesdropping. Bob randomly selects a subset of the received photons after the beam splitter. For those photons that Bob measured, he records the photons’ arrival times. Therefore, both Alice and Bob knew the arrival time of the pulses. They compare the measured results and calculate the error rate to check with the threshold. The encoding operation, that is, the polarization flip operation of the four states of single photons is realized using the two serially aligned electro-optical modulators (EO-AM-NR-C3)36. The optical axis of the two modulators is adjusted to a 45° angle. The single photons are detected using a single-photon detector (QCD300). During the eavesdropping detection procedure of the block, an optical fiber (with length L2) is used as a delay line to synchronize the encoded photons.
Schematic diagram of the experimental setup of the FRECO-DL04 protocol. PBS, Polarization beam splitter; Att, Variable attenuator; PC, Polarization controller; BS, Beam splitter; CM, Control mode; FPGA, Field programmable gate array; SPD, Single-photon detector. The distance between Alice and Bob is L1, and the delay line length is L2.
In our experiment, the highest modulation frequency f is limited by the time jitter of the single-photon detector, the computing rate of the microprocessor and the frequency response of the modulator. The channel spacing is determined by the full width at half maximum of the characteristic spectrum, which depends on the length of the photon block and the mean photon count per pulse. Here, the channel spacing is 25 kHz, which is determined by the 80 end-detected photon counts and 1 ms block time, and could be smaller under the increscent photon counts and block time.
Results and discussion
The results of the spectral analysis of the block (x(i), τi) using Equation (3) are shown in Figure 2. There is a white noise background in the frequency spectrum because the photon number of coherent light pulses obeys a Poisson distribution. There is a characteristic spectrum at the modulation frequency above the white noise background, which enables Alice to retrieve the information encoded by Bob. The noise and loss of the quantum channel decrease the SNR of the characteristic spectrum. Figure 3 shows the relationship between the signal and background noise with different mean photon numbers. With a relative larger photon number per pulse, the amplitude of the characteristic spectrum is higher than the background noise. Furthermore, our previous work37 showed that the SNR does not change with the modulation frequency. In our frequency-coding experiment, we take Nc=16 frequency channels from 25 to 400 kHz with channel spacing 25 kHz. Using a onefold frequency component r=1, which means only one of the 16 frequency channels will be used for information transmission in one time span, Alice can get log216=4 bits of information by processing one block of data in one time span. When the length of the block is 1 ms, the transmission rate reaches 4 kbps. A detailed example of the nibble of four-bit binary numbers is given in the Supplementary Information.
The experimental results of the modulation frequency spectrum. The y-axis is the Fourier-transformed amplitude in Equation (3). The different color lines represent different modulation frequencies. These 16 modulation frequency spectrum lines correspond to binary numbers from 0000 to 1111. The systematic pulse repetition frequency is 10 MHz.
The characteristic spectrum and background noise distribution of the modulation frequency spectrum. The x-axis is the mean photon count per pulse that Alice detects. The green colored areas are the background white noise in the experiment, where the color depth represents the relative probability distribution of the noise. The red line represents the amplitude of the characteristic spectrum. The modulation frequency is 200 kHz.
The security analysis of the FRECO-DL04 protocol
Here, we consider two common eavesdropping strategies: intercept-resend attack and photon-number-splitting attack. When the single-photon source is an attenuated laser with mean photon number μ per pulse, the probability pn to have n photons in a single pulse follows a Poisson distribution. The probability that an optical pulse could be detected at the receiving end is38

where is the optical attenuation due to the loss of the fiber (the total fiber length is 2L1+L2); L1 and L2 are the communication distance and the fiber length of the optical delay line at Bob’s side, respectively. α is the optical fiber loss coefficient (typical value is 0.2 dB km−1), and ηdet is the quantum efficiency of the single-photon detector39, 40. Equation (7) is valid if ηdetηpnn«1 for all n.
With multi-photon pulses, Eve performs a photon-number-splitting attack. First, she performs a quantum non-demolition measurement on the pulses as soon as they exit Alice's station. When n=2, Eve stores one photon P1 and sends the other one P2 to Bob using a lossless channel. After Bob's encoding operation, Eve captures the photon again. To gain Bob’s secret information, Eve must judge whether the polarizations of the two photons is parallel or antiparallel41. However, there is no measurement strategy for Eve to determine whether the photon P2 is flipped by Bob. Therefore, no information can be obtained by Eve from the two-photon pulses. When n=3, there is a measurement M that provides a conclusive result about whether the polarization is flipped with a probability 1/2 (Ref. 42). When n>3, we assume that Bob can always judge whether the polarization is flipped conclusively. For pulses with three or more photons, she executes M; if the outcome is not conclusive, she blocks these pulses, but if the outcome is conclusive, she prepares a new photon in the same state and forwards it to Bob. After Bob's encoding operation, Eve measures the photon again on the backward trip to see whether the polarization state has been flipped. From these operations, the mean amount of effective qubits per pulse that Eve can get is

Both eavesdropping strategies do not cause any bit error, which means that Eve cannot be detected during such an eavesdropping process.
In a noisy channel, when n=1, Eve performs the intercept-resend attack. She may gain a certain amount of data without being detected by hiding her presence in the noise if she replaces the noisy channel by an ideal one and sends another photon prepared by herself to Alice. She could acquire a fraction 4e of the qubits on the forward Alice–Bob channel, where e is the bit error rate caused by channel noise. Factor 4 arises because there is a 50% chance for Eve to pick the correct basis, but when she picks the wrong basis, there is a 50% chance of not causing a bit error. The mean effective qubits per pulse that Eve can get is

Considering all the strategies, the mean amount of effective qubits per pulse that Eve eventually gets is

The number of qubits that Alice gets and the transmission rate of Alice, respectively, can be derived from Equation (7)


where b is the bit-string length of the secret information encoded in a single-photon block, and N is the number of single photons that Alice detects within the time span Tspan. The SNR of the characteristic spectrum is determined by the number of correct detections of the encoded single photons. Although Eve may acquire some photons of the encoded single-photon block conclusively, it is impossible for her to get all secret information bits when the SNR is <1. The secure information bits per pulse and secure communication distance are shown in Figure 4. Here, we set ηdet=0.32, e=5‰, α=0.2 dB km−1, L2=L1 and C=1/2. The secure communication distance relies on the mean photon number per pulses. Typically, for weak laser pulses with mean photon number 0.1 per pulse, the secure distance is ~10 km.
The calculated transmitted information bit per pulse versus the communication distance. The dotted line is the cut-off line of the secure communication area. The solid lines with different colors represent different mean photon numbers per pulse (μ=0.19, 0.17, 0.15, 0.13, 0.11, 0.09, 0.07, 0.05, 0.03, 0.01, from top to bottom). Here, ηdet=0.32, e=5‰, α=0.2 dB km−1, L2=L1, and C=1/2.
Conclusions
In summary, we presented a new practical QSDC protocol, the FRECO-DL04 protocol, on the basis of the DL04 protocol equipped with single-photon frequency coding. Instead of quantum error correction procedure, in our protocol, the information is encoded in the modulation frequency spectrum of the single-photon block. We demonstrated the FRECO-DL04 protocol experimentally, which is the first time the block transmission has been demonstrated. With a onefold frequency component, we provided a nibble of four-bit binary numbers for direct information transmission using 16 different frequency channels. A transmission rate of 4 kbps has been achieved. The experiment firmly demonstrated the principle of QSDC with the presence of practical channel noise and loss. The FRECO-DL04 protocol could adopt multifold frequency components simultaneously, considerably increasing the amount of information that a block of single photons can carry.
References
Bennett CH, Brassard G . Quantum cryptography: public key distribution and coin tossing. In: Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India. IEEE: New York, USA; 1984, pp 175–179.
Hillery M, Bužek V, Berthiaume A . Quantum secret sharing. Phys Rev A 1999; 59: 1829–1834.
Long GL, Liu XS . Theoretically efficient high-capacity quantum-key-distribution scheme. Phys Rev A 2002; 65: 032302.
Bennett CH, Brassard G, Crépeau C, Jozsa R, Peres A et al. Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys Rev Lett 1993; 70: 1895–1899.
Bennett CH, Wiesner SJ . Communication via one- and two-particle operators on Einstein–Podolsky–Rosen states. Phys Rev Lett 1992; 69: 2881–2884.
Korzh B, Lim CCW, Houlmann R, Gisin N, Li MJ et al. Provably secure and practical quantum key distribution over 307 km of optical fibre. Nat Photonics 2015; 9: 163–168.
Bennett CH . Quantum cryptography using any two nonorthogonal states. Phys Rev Lett 1992; 68: 3121–3124.
Goldenberg L, Vaidman L . Quantum cryptography based on orthogonal states. Phys Rev Lett 1995; 75: 1239–1243.
Shimizu K, Imoto N . Communication channels secured from eavesdropping via transmission of photonic Bell states. Phys Rev A 1999; 60: 157–166.
Beige A, Englert BG, Kurtsiefer C, Weinfurter H . Secure communication with a publicly known key. Acta Phys Pol A 2002; 101: 357–368.
Boström K, Felbinger T . Deterministic secure direct communication using entanglement. Phys Rev Lett 2002; 89: 187902.
Cai QY, Li BW . Improving the capacity of the Boström–Felbinger protocol. Phys Rev A 2004; 69: 054301.
Lucamarini M, Mancini S . Secure deterministic communication without entanglement. Phys Rev Lett 2005; 94: 140501.
Long GL, Deng FG, Wang C, Li XH, Wen K et al. Quantum secure direct communication and deterministic secure quantum communication. Front Phys China 2007; 2: 251–272.
Zhu ZC, Hu AQ, Fu AM . Cryptanalysis and improvement of the controlled quantum secure direct communication by using four particle cluster states. Int J Theor Phys 2014; 53: 1495–1501.
Yoon CS, Kang MS, Lim JI, Yang HJ . Quantum signature scheme based on a quantum search algorithm. Phys Scr 2015; 90: 15103–15108.
Gao G . Two quantum dialogue protocols without information leakage. Opt Commun 2010; 283: 2288–2293.
Zheng C, Long GF . Quantum secure direct dialogue using Einstein–Podolsky–Rosen pairs. Sci China-Phys Mech Astron 2014; 57: 1238–1243.
Zhang ZJ . Multiparty quantum secret sharing of secure direct communication. Phys Lett A 2005; 342: 60–66.
Lai H, Xiao JH, Orgun MA, Xue LY, Pieprzyk J . Quantum direct secret sharing with efficient eavesdropping-check and authentication based on distributed fountain codes. Quantum Inf Process 2014; 13: 895–907.
Deng FG, Long GL, Liu XS . Two-step quantum direct communication protocol using the Einstein-Podolsky–Rosen pair block. Phys Rev A 2003; 68: 042317.
Wang C, Deng FG, Li YS, Liu XS, Long GL . Quantum secure direct communication with high-dimension quantum superdense coding. Phys Rev A 2005; 71: 044305.
Shi J, Gong YX, Xu P, Zhu SN, Zhan YB . Quantum secure direct communication by using three-dimensional hyperentanglement. Commun Theor Phys 2011; 56: 831–836.
Meslouhi A, Hassouni Y . A quantum secure direct communication protocol using entangled modified spin coherent states. Quantum Inf Process 2013; 12: 2603–2621.
Wang C, Deng FG, Long GL . Multi-step quantum secure direct communication using multi-particle Green–Horne–Zeilinger state. Opt Commun 2005; 253: 15–20.
Sun ZW, Du RG, Long DY . Quantum secure direct communication with two-photon four-qubit cluster states. Int J Theor Phys 2012; 51: 1946–1952.
Zhang QN, Li CC, Li YH, Nie YY . Quantum secure direct communication based on four-qubit cluster states. Int J Theor Phys 2013; 52: 22–27.
Wang TJ, Li T, Du FF, Deng FG . High-capacity quantum secure direct communication based on quantum hyperdense coding with hyperentanglement. Chin Phys Lett 2011; 28: 040305.
Deng FG, Long GL . Secure direct communication with a quantum one-time pad. Phys Rev A 2004; 69: 052319.
Liu D, Chen JL, Jiang W . High-capacity quantum secure direct communication with single photons in both polarization and spatial-mode degrees of freedom. Int J Theor Phys 2012; 51: 2923–2929.
Wen K, Long GL . One-party quantum-error-correcting codes for unbalanced errors: principles and application to quantum dense coding and quantum secure direct communication. Int J Quant Inform 2010; 8: 697–719.
Deng FG, Long GL . Quantum privacy amplification for a sequence of single qubits. Commun Theor Phys 2006; 46: 443–446.
Sasaki T, Yamamoto Y, Koashi M . Practical quantum key distribution protocol without monitoring signal disturbance. Nature 2014; 509: 475–478.
Shor PW, Preskill J . Simple proof of security of the BB84 quantum key distribution protocol. Phys Rev Lett 2000; 85: 441–444.
Win MZ, Scholtz RA . Ultra-wide bandwidth time-hopping spread-spectrum impulse radio for wireless multiple-access communications. IEEE Trans Commun 2000; 48: 679–689.
Abdul Khir MF, Mohd Zain MN, Suryadi, Saharudin S, Shaari S . Characterization of four states polarization flipper for single photon application. In: Proceedings of IEEE International Conference on Photonics. IEEE: Langkawi, Kedah; 2010.
Hu JY, Liu Y, Liu LL, Yu B, Zhang GF et al. Quantum description and measurement for single photon modulation. Photon Res 2015; 3: 24–27.
Scarani V, Acín A, Ribordy G, Gisin N . Quantum cryptography protocols robust against photon number splitting attacks for weak laser pulse implementations. Phys Rev Lett 2004; 92: 057901.
Zhang J, Itzler MA, Zbinden H, Pan JW . Advances in InGaAs/InP single-photon detector systems for quantum communication. Light Sci Appl 2015; 4: e286, doi:10.1038/lsa.2015.59.
Liang Y, Zeng HP . Single-photon detection and its applications. Sci China-Phys Mech Astron 2014; 57: 1218–1232.
Pryde GJ, O'Brien JL, White AG, Bartlett SD . Demonstrating superior discrimination of locally prepared states using nonlocal measurements. Phys Rev Lett 2005; 94: 220406.
Bartlett SD, Rudolph T, Spekkens RW . Optimal measurements for relative quantum information. Phys Rev A 2004; 70: 032321.
Acknowledgements
JY Hu, B Yu, MY Jing, LT Xiao and ST Jia are sponsored by the 973 Program (No. 2012CB921603), 863 Program (No. 2011AA010801), the Natural Science Foundation of China (Nos. 61527824, 11374196, 10934004 and 11204166) and PCSIRT (No. IRT 13076). GQ Qin and GL Long are supported by the Natural Science Foundation of China (Nos. 11175094 and 91221205) and the National Basic Research Program of China (No. 2015CB921001).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications' website.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hu, JY., Yu, B., Jing, MY. et al. Experimental quantum secure direct communication with single photons. Light Sci Appl 5, e16144 (2016). https://doi.org/10.1038/lsa.2016.144
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2016.144
Keywords
This article is cited by
-
Device-independent quantum secure direct communication under non-Markovian quantum channels
Quantum Information Processing (2024)
-
Quantum secure direct communication with hybrid entanglement
Frontiers of Physics (2024)
-
Recent progress in quantum photonic chips for quantum communication and internet
Light: Science & Applications (2023)
-
Statistical fluctuation analysis for decoy-state quantum secure direct communication
Quantum Information Processing (2023)
-
Realization of quantum secure direct communication over 100 km fiber with time-bin and phase quantum states
Light: Science & Applications (2022)