Abstract
The terahertz region is a special region of the electromagnetic spectrum that incorporates the advantages of both microwaves and infrared light waves. In the past decade, metamaterials with effective medium parameters or gradient phases have been studied to control terahertz waves and realize functional devices. Here, we present a new approach to manipulate terahertz waves by using coding metasurfaces that are composed of digital coding elements. We propose a general coding unit based on a Minkowski closed-loop particle that is capable of generating 1-bit coding (with two phase states of 0 and 180°), 2-bit coding (with four phase states of 0, 90°, 180°, and 270°), and multi-bit coding elements in the terahertz frequencies by using different geometric scales. We show that multi-bit coding metasurfaces have strong abilities to control terahertz waves by designing-specific coding sequences. As an application, we demonstrate a new scattering strategy of terahertz waves—broadband and wide-angle diffusion—using a 2-bit coding metasurface with a special coding design and verify it by both numerical simulations and experiments. The presented method opens a new route to reducing the scattering of terahertz waves.
Similar content being viewed by others
Introduction
According to the International Telecommunications Union (ITU), terahertz radiation comprises the electromagnetic waves in the frequency band from 300 GHz to 3000 GHz (or 3 THz), with corresponding wavelengths ranging from 1 mm to 0.1 mm. Because the terahertz frequency region lies between microwaves and infrared light in the electromagnetic spectrum, terahertz waves combine the advantages of the two bands, including their nonionizing radiation, high resolution, and good penetration into nonconducting materials; however, terahertz waves cannot penetrate into liquid water or metal1. Compared with optics, infrared, and microwaves, the terahertz wave is a new subject, and the related technology is still in its infancy. Among the many theories and technologies considered in the study of terahertz waves, the control of terahertz wave scattering is especially important.
In the past decade, metamaterials that are composed of artificially resonant particles2,3 have been presented to manipulate electromagnetic waves4,5,6,7,8,9,10,11,12 in applications such as computation and imaging13,14. Computational metamaterials, which can perform mathematical operations13, are much smaller than conventional lens-based optical signal-processing systems. A combination of metamaterials and a compressed imaging approach has achieved a low-profile microwave imaging method14. Transformation optics (TO) is a powerful tool to avoid electromagnetic scattering around objects by using gradient-index (GRIN) media15,16,17,18,19,20, which can deflect the terahertz waves and guide them around the objects without perturbing the exterior fields4,5. However, the drawbacks of the TO method are the rigorous material parameter requirements (permittivity and/or permeability) and the large cloak volumes, which restrict the practical applications. To avoid the material requirement limitations, ultrathin mantle cloaks were wrapped around the objects to cancel part of the scattered waves and thereby achieve transparency based on the Mie scattering21,22,23. With the increase in the object dimensions, however, the contributions from higher-order Mie scattering coefficients become more important, which introduce great challenges in designing the mantle cloak. An alternative method for the development of stealth objects is to use a metamaterial absorber24,25,26,27,28, which relies on the simultaneous electric and magnetic responses near the working frequency, resulting in resonant absorption and the multiple-reflection cancelation of terahertz waves6,7. Because of its resonant nature, however, the bandwidth of the metamaterial absorber is limited.
Recently, the strong interaction between electromagnetic waves and the metasurface has been a topic of considerable interest29,30,31,32,33. It was shown that a metasurface with periodic gradient phase shifts from 0 to 2π can generate anomalous reflections and refractions, which yields a generalized Snell’s law29. Based on similar principles, other physical phenomena have been investigated using gradient-phase metasurfaces, such as optical vortexes29, light bending30, the photonic spin Hall effect31, polarization traffic control32, and the efficient conversion of surface plasmon polaritons33. When the local reflection phases of unit cells are randomly distributed, the metasurfaces can be used to reduce the scatter fields of the microwaves34,35. In the terahertz frequencies, metasurfaces have also played important roles in producing novel functionalities8,9,10,11,12, including high-efficiency terahertz modulators based on active metamaterial particles8,9, low-loss polarization conversions10, and the abnormal reflections and transmissions of terahertz waves10,11,12. More recently, an alternative approach has been reported to control electromagnetic waves using coding metamaterials36, instead of the conventional metamaterials described by effective medium parameters or gradient phases2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35, in which one can manipulate the electromagnetic scattering and radiation by designing the coding sequences of digital particles36,37. Based on this idea, digitally controlled metamaterials and programmable metamaterials have been realized in the microwave frequencies36.
In this article, we propose a new strategy in controlling terahertz waves to realize broadband and wide-angle diffusion by using coding metasurfaces. We present a general coding unit cell based on the Minkowski closed-loop particle, whose multi-resonance feature helps achieve multi-bit coding elements and broaden the bandwidth of coding metasurfaces. By designing appropriate coding sequences, the multi-bit coding metasurfaces have the strong ability to manipulate terahertz waves. As an application, we design a special 2-bit coding metasurface to demonstrate the broadband and wide-angle diffusion of terahertz waves, which are verified by both numerical simulations and experiments.
Materials and methods
Coding metasurface and Minkowski fractal coding particle
Different from conventional metamaterials, coding metamaterials are composed of digital elements and are controlled by the coding sequences of these digital elements36. For 1-bit coding metamaterials, the basic digital elements are “0” and “1”, whose reflection responses to electromagnetic waves have the same amplitude but opposite phase (0 and ±180°). For 2-bit coding metamaterials, the basic digital elements are “00”, “01”, “10”, and “11”, whose reflection responses have the same amplitude and the four phase states of 0, ±90°, ±180°, and ±270°. Similarly, 3-bit coding metamaterials have eight digital elements, “000”, “001”, “010”, “011”, “100”, “101”, “110”, and “111”, with the same amplitude and the phases 0, ±45°, ±90°, ±135°, ±180°, ±225°, ±270°, and ±315°. We note that the digital elements may have other definitions, but the above-defined elements will be easily digitally controlled in the future study.
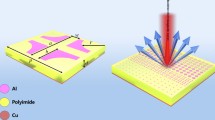
Coding metamaterials or metasurfaces can be used to control electromagnetic waves by designing the coding sequences36. Here, we propose a coding metasurface to change the peak scattering of terahertz waves to diffusion, as sketched in Figure 1a. Under the illumination of terahertz waves on the coding metasurface, all particles are driven by a special coding sequence, which results in the reflected energy redistributing in numerous directions, thereby creating electromagnetic diffusion. To build up the coding metasurface, we propose a Minkowski loop as the coding particle. As illustrated in Figure 1b, the Minkowski loop has fractal geometry with an excellent self-similar property, which is useful for minimizing the unit size and broadening the working bandwidth38. Generally, the Minkowski loop is constructed by an iterative procedure from the starting geometry of a square. Each of the four straight segments of the starting structure is replaced with the generator. Here, we only use the first-order Minkowski loop as the basic particle in our design. From full-wave simulations, we obtain the electric-field distributions excited in the substructures of the loop, as shown in Figure 2a and 2b, in which the electric fields reach maximums at different positions, showing strong reflections on the fractal surface. The calculated reflection coefficients are demonstrated in Figure 2c, from which two resonances are observed at 0.8 and 1.6 THz, with significant absorptions. The close resonances are helpful for broadening the bandwidth of the coding particle and improving the phase linearity required by our design.
Coding metasurface and Minkowski coding particle. (a) Schematic of a coding metasurface illuminated by terahertz waves, showing the occurrence of electromagnetic diffusion in the upper half-space. (b) The Minkowski coding particle at the first iteration. The lattice constant of the coding particle is Λ = 90 μm (equal to 0.3λ at 1.0 THz), and the length of the coding metasurface is 7.56 mm (equal to 25.2λ at 1.0 THz).
Multi-bit Minkowski coding particles
The magnitude and phase responses of Minkowski loops with different scales are shown in Figure 3a and 3b, respectively, in which L is the loop width. From Figure 3a, we observe that the phase curves are almost parallel to the change in L, which is important to guarantee the working bandwidth of the coding particle. We also note high-reflection amplitudes with small variations below the frequency of 1.7 THz in Figure 3b, which indicates small resonance absorptions on the metasurface. To provide full control of the scattering patterns, we calculate the available phase range at different frequencies by changing the loop width, as illustrated in Figure 4a. Clearly, we can obtain significant phase coverage larger than 270° between 0.8 and 1.7 THz because of the double resonances of the loop (see Figure 2a and 2b).
Designs of the Minkowski coding particles. (a) The available phase coverage for the Minkowski loop in the frequency range from 0.5 to 1.7 THz. (b) The dependence of the phase on the loop width L with fixed dimensions Λ = 90 μm, w = 5 μm, g = 15 μm, and Lin = 33 μm. (c) The designed 1-, 2-, and 3-bit coding particles using different-scale Minkowski loops.
To design coding particles using the Minkowski loops, we extract reflection phases with different loop scales at the central frequency of 1.4 THz, as depicted in Figure 4b. Amazingly, the phase has a nearly linear relation to the loop width L, which is crucial for designing multi-bit coding particles using the same geometry. Here, the lattice constant of the Minkowski loop is Λ = 90 μm, equal to 0.3λ at the frequency of 1.0 THz. From Figure 4b, we read the reflection phases at 0, −45°, −90°, −135°, −180°, −225°, −270°, and −315° as L = 43 μm, 46 μm, 52 μm, 57.5 μm, 63 μm, 67.5 μm, 71 μm, and 75.5 μm, respectively. Hence, the Minkowski loops with scales L = 43 μm and 63 μm can be used as the 1-bit coding particles “0” and “1”, 2-bit coding particles “00” and “10”, and 3-bit coding particles “000” and “100”; the Minkowski loops with scales L = 52 μm and 71 μm can be used as the 2-bit coding particles “01” and “11”, and 3-bit coding particles “010” and “110”; and the Minkowski loops with scales L = 46 μm, 57.5 μm, 67.5 μm, and 75.5 μm can be used as the 3-bit coding particles “001”, “011”, “101”, and “111”. This is clearly shown in Figure 4b and 4c. Similarly, the Minkowski loop can also be used as higher-bit coding particles. Because of their four-fold geometrical symmetry, the coding particles are insensitive to the polarization states of the incident terahertz waves.
Results and discussion
Diffusion coding metasurface and design
The principle to generate terahertz diffusion using coding metasurfaces can be easily understood from classical electromagnetic theory. In fact, one could control the scattering features of coding metasurfaces by changing the coding sequences33. When the coding particles are regularly arranged, the scattering pattern indicates the spatial distribution of the reflected energies under the normal illumination of planar terahertz waves. For example, in the 1-bit coding with all “1” elements (see Figure 5a), the coding metasurface is actually a perfectly electric conducting surface; hence, a highly directed backward terahertz beam is observed from Snell’s law, as shown in Figure 5d. In the case of 1-bit coding with a chessboard “0” and “1” distribution (Figure 5b), the reflected terahertz energy will be split into four main beams (Figure 5e), whereas in the case of 2-bit coding with a periodic “00”“01”/“11”“10” distribution (Figure 5c), 12 reflected terahertz beams are generated under the normal incidence, as shown in Figure 5f. We observe that the backward scattering reduction arises from the abrupt phase shifts between adjacent units on the coding metasurfaces, which leads to the anomalous reflections. With the increase in the number of bits, the reflected terahertz energy is scattered in more directions, and the scattering width of the coding metasurface is thus dramatically decreased.
The scattering features of periodic arrangements of coding particles. (a) The 1-bit coding with all “1” elements. (b) The 1-bit coding with the chessboard “0” and “1” distribution. (c) The 2-bit coding with the periodic “00”“01”/“11”“10” distribution. (d–f) The simulated scattering patterns of the 1- and 2-bit coding sequences shown in a–c.
From the above analysis, the periodic arrangement of the coding particles allows for a formidable control of the scattering pattern in generating multiple beams. However, the maximum scattering directions are usually fixed. To realize terahertz diffusion on a planar coding metasurface, we propose a scheme so that all coding particles of the metasurface are randomly arranged to achieve the desired diverse scattering pattern. In this scheme, a particle-swarm optimization algorithm is employed to find the optimal arrangement of coding elements. During the optimization, we use a far-field pattern prediction algorithm35 as an auxiliary module to save the effort required for tremendous full-wave simulations. Here, the equivalent conducting current, magnetic current, and electric current of each coding element are extracted by the numerical simulation of the unit cell, and they can be used to rapidly predict the scattering pattern of the coding metasurface.
As an example, we consider a 2-bit coding diffusion metasurface with a large area of 7.56 × 7.56 mm2 (25.2λ × 25.2λ at 1.0 THz), which contains 84 × 84 = 7056 coding particles that are constructed by Minkowski loops on a polyimide layer by incorporating conventional photolithography. Each coding particle occupies an area of 90 × 90 μm2 (0.3λ × 0.3λ at 1.0 THz). After some iterations of optimization, the arrangement of the 2-bit coding particles is determined, as illustrated in Figure 6a, including a zoomed view on a small area to clearly show the particles. Figure 7a–7c illustrates the simulated three-dimensional (3D) scattering patterns of the designed 2-bit coding metasurface at 1, 1.4, and 1.8 THz, respectively, in which the diffusion behaviors of the scattered fields are clearly observed in a wide frequency band. To demonstrate the diffusion effects quantitatively, we depict the scattering patterns at the above frequencies on E-planes in Figure 7d–7f. For comparison, we provide the corresponding E-plane scattering patterns of the bare metal surface in Figure 7g–7i, showing significant scattering in the backward direction (i.e., total reflection). Comparing the two sets of scattering patterns, we note that there are numerous scattering beams in the upper space, but the scattering levels of all of the beams are significantly suppressed, which results in a nearly omnidirectional scattering.
Numerical simulation results of a 2-bit diffusion coding metasurface. (a–c) 3D scattering patterns of the 2-bit coding metasurface at 1, 1.4, and 1.8 THz, which show the significant diffusion effects. (d–f) E-plane scattering patterns of the 2-bit coding metasurface at 1, 1.4, and 1.8 THz. (g–i) E-plane scattering patterns of a bare metal plate with the same dimensions at 1, 1.4, and 1.8 THz.
Sample fabrication and experiments
The fabrication procedure of the coding metasurface sample is presented in Figure 8a. First, we sputtered a gold (Au) film on a silicon wafer as the reflecting plane and then coated the film with polyimide jelly as the dielectric layer, which was spun cast at a preset rotating speed for 45 s. To solidify the polyimide jelly and control its permittivity, we baked the jelly at 80, 120, 180, and 250°C for 5 min. The final thickness of the polyimide layer was 30 μm, which was approximately one-tenth of the wavelength at 1.0 THz. Then, the photoresist LOR and AZ5214 were coated on the polyimide layer through a phase mask and exposed to ultraviolet radiation generated by an Hg lamp. The photoresist must also be baked at 95°C for 1.5 min for solidification. The exposed photoresist was rinsed off in the areas where the target pattern was to be located, and a second Au layer with a thickness of 200 nm was sputtered on the disposed photoresist. Finally, both the residual photoresist and metal were removed by dipping them into acetone, and the rest of metal formed the target pattern on its upper layer. A part of the fabricated 2-bit coding diffusion metasurface is shown in Figure 8b.
The fabrication and measurement results of the coding metasurface. (a) The fabrication process for the coding metasurface. (b) Part of the fabricated sample of the 2-bit diffusion coding metasurface. (c) The measured and simulated backward scattering coefficients of the 2-bit coding metasurface in the frequency range from 0.8 to 2 THz under normal incidence. Sim., Simulative; Exp., Experimental.
To observe the scattering properties of the metasurface, a custom-built detection system is used to measure the scattering coefficients as functions of the scattering angle and operating frequency, as illustrated in Figure 9. The fabricated sample is mounted on a metal frame in the experiments. A pair of fiber-coupled photoconductive antennas is used for both the emission and the detection. The pump laser source is capable of generating pulses at a width of 84 fs at the central wavelength 1.550 μm, corresponding to a spectral wavelength of 42.4 nm, and the reception rate is 100 MHz. The laser pulse is coupled into a dispersion compensating fiber followed by a fiber-optic splitter. Then, the laser is split into a pump beam and a probe beam. The probe beam is collimated by a GRIN lens when it exits the fiber. After propagation in the air, the laser is coupled into another identical GRIN lens, which is attached with a fiber pigtail. The required temporal delay between the terahertz pulse and probing laser pulse is produced by moving the GRIN lens coupler. A half-wave plate is inserted between the GRIN lenses to optimize the detected signal. Two off-axis parabolic mirrors are used to collect and collimate the terahertz beams, and they are both mounted on guide rails and fixed with a THz emitter and detector, respectively. The incident and reflected angles can be easily changed by rotating the guide rails. The scattering signal is detected using the photoconductive sampling method.
The measured backward scattering coefficients (or the reflection coefficients) of the 2-bit coding metasurface in the frequency range from 0.8 to 2 THz under normal incidence are recorded in Figure 8c in comparison to a same-sized control Au plate without the metasurface. We also provide the simulation results of the metasurface in the same figure and show good agreement with the measured results. In the numerical simulations, we set the substrate permittivity as ε = 3.0 + i0.03, but the actual value may exhibit a slight deviation because it is easily influenced by fabrication error. From Figure 8c, we observe that the coding metasurface shows an excellent diffusion property in the broad frequency band from 0.8 to 1.8 THz with significant backward scattering suppression.
Similarly, the diffusion behaviors of terahertz waves can be achieved by using 1- and 3-bit coding metasurfaces. Based on the same design procedure, we obtain the 1- and 3-bit coding distributions on an area of 7.56 × 7.56 mm2 (25.2λ × 25.2 λ at 1.0 THz), as shown in Figure 6b and 6c, respectively, which contains 7056 Minkowski coding particles. Under the normal incidences of terahertz waves at two arbitrarily chosen frequencies (1.1 and 1.0 THz), the simulated 3D scattering patterns and E-plane scattering patterns of the 1- and 3-bit coding metasurfaces are illustrated in Figure 10a, 10b, 10d and 10e, respectively. Compared with the total-reflection results of bare Au plates without metasurfaces presented in Figure 10c and 10f, we clearly notice the diffusion effects of the 1-bit and 3-bit coding metasurfaces. The broadband features of the terahertz diffusion caused by the 1- and 3-bit coding metasurfaces are illustrated in Figure 10g, which shows the powerful abilities of multi-bit coding metasurfaces to control the scattering of terahertz waves.
Numerical simulation results of 1-bit and 3-bit diffusion coding metasurfaces. (a) 3D scattering pattern of the 1-bit coding metasurface at 1.1 THz. (b) E-plane scattering pattern of the 1-bit coding metasurface at 1.1 THz. (c) E-plane scattering pattern of a bare metal plate with the same dimensions at 1.1 THz. (d) 3D scattering pattern of the 3-bit coding metasurface at 1 THz. (e) E-plane scattering pattern of the 3-bit coding metasurface at 1 THz. (f) E-plane scattering pattern of a bare metal plate with the same dimensions at 1 THz. (g) Simulated backward scattering coefficients of the 1- and 3-bit coding metasurfaces in the frequency range from 0.8 to 2 THz under normal incidence.
To investigate the angular dependence of the scattering profiles, three incident angles (20°, 30°, and 40° with respect to the surface normal) are considered in our experiments. Under the oblique incidences, the scattering coefficients in the specular reflection directions based on Snell’s law (see insets of Figure 11a, 11c and 11e) are first measured. Figure 11a, 11c and 11e shows the measured reflection coefficients of the 2-bit coding metasurface when the terahertz waves are incident at 20°, 30°, and 40° across the wide frequency band (0.5–1.6 THz), respectively, and exhibit excellent performance in diffusing the terahertz waves in the specular scattering directions. In viewing the scattering properties at other observation angles, we present the measured results of the scattering coefficients over wide angles from 20° to 80° in the broad frequency range from 0.5 to 1.8 THz in Figure 11b, 11d and 11f under incident angles of 20°, 30°, and 40°, respectively. From these figures, we can clearly observe small scattering peaks when the observation angles equal the incident angles (i.e., the specular scattering directions), whereas the scattered fields at the other observation angles are relatively small, which confirms the good diffusion behavior.
Measurement results of the 2-bit diffusion coding metasurface under the oblique incidences. (a, c, e) Measured scattering coefficients in the specular directions of the 2-bit coding metasurface in the frequency range from 0.5 to 1.6 THz under the oblique incidences of 20°, 30°, and 40°, respectively. (b, d, f) Measured scattering coefficients in wide angles from 20° to 80° of the 2-bit coding metasurface in the frequency range from 0.5 to 1.6 THz under the oblique incidences of 20°, 30°, and 40°, respectively. Inc., Incidence; Refl., Reflection.
Conclusions
We have proposed a new coding particle based on the Minkowski closed loop that is capable of generating 1-, 2-, and 3-bit coding elements in the terahertz frequencies using different geometric scales. We have shown that multi-bit coding metasurfaces have the strong ability to control terahertz waves by the use of different coding distributions. In particular, we demonstrated the broadband and wide-angle diffusion of terahertz waves numerically and experimentally using a 2-bit coding metasurface. The coding distribution was randomly arranged to achieve the desired electromagnetic diffusion of scattering waves. The sample coding metasurface was fabricated by a standard photolithography method, and the scattering patterns were measured in a self-built system, where both the angular and frequency dependences were considered in experiments. The measured results have a good match to numerical simulations and show the excellent diffusion behavior of terahertz waves in broadband and wide angles. The proposed method opens new possibilities to control the scattering of terahertz waves and paves the way to develop more coding devices in the future.
References
Zhang XC, Xu J . Introduction to THz Wave Photonics. New York: Springer Science & Business Media; 2010.
Cui TJ, Smith DR, Liu R . Metamaterials: Theory, Design, and Applications. New York: Springer Science & Business Media; 2009.
Chen H, Chan CT, Sheng P . Transformation optics and metamaterials. Nat Mater 2010; 9: 387–396.
Zhou F, Bao Y, Cao W, Stuart CT, Gu J et al. Hiding a realistic object using a broadband terahertz invisibility cloak. Sci Rep 2011; 1: 78.
Chen PY, Alù A . Atomically thin surface cloak using graphene monolayers. ACS Nano 2011; 5: 5855–5863.
Tao H, Landy NI, Bingham CM, Zhang X, Averitt RD et al. A metamaterial absorber for the terahertz regime: design, fabrication and characterization. Opt Express 2008; 16: 7181–7188.
Tao H, Bingham CM, Strikwerda AC, Pilon D, Shrekenhamer D et al. Highly flexible wide angle of incidence terahertz metamaterial absorber: design, fabrication, and characterization. Phys Rev B 2008; 78: 241103.
Chen HT, Padilla WJ, Cich MJ, Azad AK, Averitt RD et al. A metamaterial solid-state terahertz phase modulator. Nat Photonics 2009; 3: 148–151.
Chen HT, Padilla WJ, Zide JM, Gossard AC, Taylor AJ et al. Active terahertz metamaterial devices. Nature 2006; 444: 597–600.
Grady NK, Heyes JE, Chowdhury DR, Zeng Y, Reiten MT et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 2013; 340: 1304–1307.
Zhang X, Tian Z, Yue W, Gu J, Zhang S et al. Broadband Terahertz wave deflection based on C-shape complex metamaterials with phase discontinuities. Adv Mater 2013; 25: 4566–4572.
Huang L, Chen X, Mühlenbernd H, Zhang H, Chen S et al. Three-dimensional optical holography using a plasmonic metasurface. Nat Commun 2013; 4: 2808.
Silva A, Monticone F, Castaldi G, Galdi V, Alù A et al. Performing mathematical operations with metamaterials. Science 2014; 343: 160–163.
Hunt J, Driscoll T, Mrozack A, Lipworth G, Reynolds M et al. Metamaterial apertures for computational imaging. Science 2013; 339: 310–313.
Pendry JB, Schurig D, Smith DR . Controlling electromagnetic fields. Science 2006; 312: 1780–1782.
Leonhardt U . Optical conformal mapping. Science 2006; 312: 1777–1780.
Schurig D, Mock JJ, Justice BJ, Cummer SA, Pendry JB et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006; 314: 977–980.
Liu R, Ji C, Mock JJ, Chin JY, Cui TJ et al. Broadband ground-plane cloak. Science 2009; 323: 366–369.
Ergin T, Stenger N, Brenner P, Pendry JB, Wegener M . Three-dimensional invisibility cloak at optical wavelengths. Science 2010; 328: 337–339.
Ma HF, Cui TJ . Three-dimensional broadband ground-plane cloak made of metamaterials. Nat Commun 2010; 1: 21.
Soric JC, Chen PY, Kerkhoff A, Rainwater D, Melin K et al. Demonstration of an ultralow profile cloak for scattering suppression of a finite-length rod in free space. New J of Phys 2013; 15: 033037.
Chen PY, Alù A . Mantle cloaking using thin patterned metasurfaces. Phys Rev B 2011; 84: 205110.
Chen PY, Soric J, Alù A . Invisibility and cloaking based on scattering cancellation. Adv Mater 2012; 24: OP281–OP304.
Landy NI, Sajuyigbe S, Mock JJ, Smith DR, Padilla WJ . Perfect metamaterial absorber. Phys Rev Lett 2008; 100: 207402.
Aydin K, Ferry VE, Briggs RM, Atwater HA . Broadband polarization-independent resonant light absorption using ultrathin plasmonic super absorbers. Nat Commun 2011; 2: 517.
Liu X, Starr T, Starr AF, Padilla WJ . Infrared spatial and frequency selective metamaterial with near-unity absorbance. Phys Rev Lett 2010; 104: 207403.
Chen HT, Zhou J, O’Hara JF, Chen F, Azad AK et al. Antireflection coating using metamaterials and identification of its mechanism. Phys Rev Lett 2010; 105: 073901.
Shen X, Cui TJ, Zhao J, Ma HF, Jiang WX et al. Polarization-independent wide-angle triple-band metamaterial absorber. Opt Express 2011; 19: 9401–9407.
Yu N, Genevet P, Kats MA, Aieta F, Tetienne JP et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 2011; 334: 333–337.
Ni X, Emani NK, Kildishev AV, Boltasseva A, Shalaev VM . Broadband light bending with plasmonic nanoantennas. Science 2012; 335: 427.
Yin X, Ye Z, Rho J, Wang Y, Zhang X . Photonic spin Hall effect at metasurfaces. Science 2013; 339: 1405–1407.
Lin J, Mueller JP, Wang Q, Yuan G, Antoniou N et al. Polarization-controlled tunable directional coupling of surface plasmon polaritons. Science 2013; 340: 331–334.
Sun S, He Q, Xiao S, Xu Q, Li X et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat Mater 2012; 11: 426–431.
Yang XM, Zhou XY, Cheng Q, Ma HF, Cui TJ . Diffuse reflections by randomly gradient index metamaterials. Opt Lett 2010; 35: 808–810.
Wang K, Zhao J, Cheng Q, DS Dong, Cui TJ . Broadband and broad-angle low-scattering metasurface based on hybrid optimization algorithm. Sci Rep 2014; 4: 5935.
Cui TJ, Qi MQ, Wan X, Zhao J, Cheng Q . Coding metamaterials, digital metamaterials and programmable metamaterials. Light: Sci & Appl 2014; 3: e218; doi:10.1038/lsa.2014.99.
Giovampaola CD, Engheta N . Digital metamaterials. Nat Mater 2014; 13: 1115–1121.
Dhar S, Ghatak R, Gupta B, Poddar DR . A wideband Minkowski fractal dielectric resonator antenna. IEEE Trans on Antennas Propag 2013; 61: 2895–2903.
Acknowledgements
This work was supported by the National High Tech Projects (2012AA030402 and 2011AA010202), the National Science Foundation of China (61138001, 61171024, 61171026, 61371035 and 11227904), the 111 Project (111-2-05), the Natural Science Foundation of Jiangsu Province (BK2012019), and the 973 Program (2014CB339800).
Note: Accepted article preview online 30 April 2015
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
This license allows readers to copy, distribute and transmit the Contribution as long as it is attributed back to the author. Readers are permitted to alter, transform or build upon the Contribution as long as the resulting work is then distributed under this or a similar license. Readers are not permitted to use the Contribution for commercial purposes. Please read the full license for further details at - http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Gao, LH., Cheng, Q., Yang, J. et al. Broadband diffusion of terahertz waves by multi-bit coding metasurfaces. Light Sci Appl 4, e324 (2015). https://doi.org/10.1038/lsa.2015.97
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2015.97
Keywords
This article is cited by
-
Terahertz wavefront engineering using a hard-coded metasurface
Optical and Quantum Electronics (2023)
-
Single-Row Coding Metasurface for Bi-directional Beam Multiplexing in Mid-infrared Regime
Plasmonics (2023)
-
Suppressing meta-holographic artifacts by laser coherence tuning
Light: Science & Applications (2021)
-
Phase-to-pattern inverse design paradigm for fast realization of functional metasurfaces via transfer learning
Nature Communications (2021)
-
A wireless communication scheme based on space- and frequency-division multiplexing using digital metasurfaces
Nature Electronics (2021)