Abstract
The multicore fiber (MCF) is a physical system of high practical importance. In addition to standard exploitation, MCFs may support discrete vortices that carry orbital angular momentum suitable for spatial-division multiplexing in high-capacity fiber-optic communication systems. These discrete vortices may also be attractive for high-power laser applications. We present the conditions of existence, stability, and coherent propagation of such optical vortices for two practical MCF designs. Through optimization, we found stable discrete vortices that were capable of transferring high coherent power through the MCF.
Similar content being viewed by others
Introduction
Vortex structures are widespread in nature and are found in both macroscopic atmospheric phenomena, such as tornadoes and the Great Red Spot of Jupiter, and microscopic-scale objects in quantum physics. Mathematically, vortices are related to topological defects, the accumulation of geometrical phases, and the phase singularity of a complex linear or nonlinear field (see, e.g., Refs. 1,2,3,4,5,6,7,8 and references therein).
Optical vortices present a fascinating and expanding area of research that combines fundamental theoretical and mathematical science and maturing applied technologies (see recent review4). Optical vortices are characterized by a wave field with zero intensity, an undefined phase in the vortex center (pivot point) and the presence of a screw dislocation of the wave front5,6. All transmutations of vortices in linear and nonlinear fields obey the conservation of the topological charge S, which is defined as the total change of the phase along a closed curve surrounding the pivotal point of the vortex divided by 2π. The special behavior of the phase and amplitude near the vortex pivot point results in the circular flow of energy in optical vortices7,8,9,10. This property is closely related to the ability of optical vortices to carry orbital angular momentum and energy11,12,13,14. This property is interesting for various applications, such as in optical traps15,16,17, information transmission18,19,20, astrophysics21,22, microscopy23,24, and laser micromachining25,26.
In nonlinear media, optical vortices are treated as (topological) vortex solitons4,27,28. Such topologically stable pulses can act as information carriers4,29,30,31. It is important that continuum vortex solitons are highly sensitive to azimuthal instability. Stabilization is possible by applying optically induced photonic lattices, which lead to a discrete optical vortex field. Different types of discrete lattice vortex solitons were theoretically predicted in the Refs. 32,33,34,35 and experimentally demonstrated in the Refs. 36,37. Discrete vortex solitons can also be created in photonic crystal fibers and other types of photonic lattices38,39. Discrete vortex solitons are frequently associated with soliton clusters, which feature interesting mobility properties and rotating propagation29,30,31,40,41,42. The existence and stability of multidimensional spatiotemporal solitons (more precisely, solitary waves) in different physical settings were theoretically analyzed in the Refs. 43,44. The spatiotemporal optical solitons in fiber arrays were studied in the Ref. 45, and the corresponding spatiotemporal optical vortices were studied theoretically in the Refs. 46,47 and experimentally in the Ref. 48.
Light vortices as carriers of orbital angular momentum can support spatial-division multiplexing, which is an actively studied topic in high-speed optical communications, given the increasing demand for capacity in global communications systems. Multimode49 or multicore fibers (MCFs)50,51,52 may be used for such spatial-division multiplexing. Recently, the nonlinear effects in MCF were examined in the Refs. 53,54, and the results indicated fascinating new features (compared with both infinite photonic lattices and single core fibers). Mathematical models of MCFs are based on the nonlinear Schrödinger equation4,53,54 or the nonlinear complex Ginzburg-Landau equation27,28,55,56. The latter model describes an active MCF media with loss and gain effects included during light propagation.
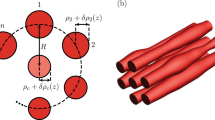
In this study, we present nonlinear wave solutions in the form of discrete optical vortices that demonstrate stable coherent propagation in MCF structures, as shown in Figure 1, which is modeled using the discrete nonlinear Schrödinger equation53,54. Compared with the uniform 2D rectangular and triangular lattices, this MCF structure possesses different symmetry and has a reduced degree of freedom imposed by the geometrical constrains on the coupling between the waveguides, which affects the properties of the vortex structures. Through analytical and numerical analysis, we present the results on the existence, stability, and dynamic properties of such structures. We demonstrate the remarkable features of the vortices with some phase profiles and define the number of peripheral cores to enable coherent transmission of high optical power that is limited only by the applicability of the model. This property is of particular interest for designing new types of switches, sources of high brightness, coherent radiation or uniform light sources using tailored phase profiles.
Materials and methods
The master model of practical MCFs (Figure 1) is derived starting from the Helmholtz equation57 and is based on a low-dimensional version of the discrete nonlinear Schrödinger equation in a weak coupling approximation, for which only the interaction between neighboring cores is important53.

In the MCF model Equation (1), Am is the complex amplitude of the optical field in the mth periphery core, M is the number of periphery cores, A0 is the corresponding amplitude in the central core and βm and β0 denote propagation constants of the optical fields in the periphery and central cores, respectively. We consider the MCF both without (Figure 1, left) (in this case A0 = 0 always) and with (Figure 1, right) a central core. The periphery cores are assumed to be identical to ensure that the propagation constants are equal, βm = β1, the coupling coefficients are equal, Cm,m – 1 = Cm,m + 1 = C1, and the nonlinearity parameters γm = γ1 for all m = 1, …, M. The corresponding quantities for the central core are β0, C0,m = C0, m = 1, …, M, γ0 and differ from these quantities on the periphery. Therefore, Equation (1) can be rewritten in the following form:

We present dynamically stable vortices with topological charge S = 1, 2, 3, 4 in a nonlinear MCF system with a small number of periphery cores, M = 3, 4, …, 17.
The form of stationary discrete vortices characterized by the topological charge S is defined by the following:

where μ is the propagation constant of the vortex solution. Note that  for any integer S.
for any integer S.
The system supports vortex solutions with topological charge S and amplitude

in the region of parameters derived from the condition A2 > 0, namely,  . In contrast to the linear case,
. In contrast to the linear case,  , in which the amplitude is arbitrary and does not affect the properties of the linear vortices, in the nonlinear case, the vortex properties are power dependent. The most important feature is that the phase matching condition required for coherent propagation in multiple cores depends on the power. Finally, although S/M is a rationale number in general, note that in the cases for which S/M = n (where n is an integer) and S/M = 1/2, the phase increments (α) are multiplies of 2π or π, and the vortex amplitudes are purely real.
, in which the amplitude is arbitrary and does not affect the properties of the linear vortices, in the nonlinear case, the vortex properties are power dependent. The most important feature is that the phase matching condition required for coherent propagation in multiple cores depends on the power. Finally, although S/M is a rationale number in general, note that in the cases for which S/M = n (where n is an integer) and S/M = 1/2, the phase increments (α) are multiplies of 2π or π, and the vortex amplitudes are purely real.
By varying the values of an integer parameter S and the number of periphery cores M, we analytically derived and numerically verified the parameter ranges in which stable vortices can propagate. The steady-state vortices were found numerically through the use of a nonlinear equation solver based on the Powell method58, whereas the vortex propagation was simulated using a sixth-order Runge-Kutta numerical procedure.
The two conserved quantities characterize the light propagation through the MCF system described with model Equation (2), and the quantities are the norm (total power) P and the Hamiltonian H:

Now, we perform a linear stability analysis both analytically and numerically. By considering small perturbations on the background of the vortex solutions in Equation (2) given by

and after linearization, we obtain the following eigenvalue problem:

Equation (6) and the corresponding complex conjugate can be written in matrix form:

where δA is a column matrix of small perturbations,  , and
, and  is the corresponding eigenvalue 2N × 2N matrix, where N is the total number of cores in the MCF system; N = M or N = M + 1 in the case without or with a central core characterized by 2N eigenvalues, respectively. In general, the matrix
is the corresponding eigenvalue 2N × 2N matrix, where N is the total number of cores in the MCF system; N = M or N = M + 1 in the case without or with a central core characterized by 2N eigenvalues, respectively. In general, the matrix  is non-Hermitian, and the type of eigenvalues (real – stability, pure imaginary – exponential instability or complex – oscillatory instability) depends on the values of the matrix elements and, consequently, on the parameters (
is non-Hermitian, and the type of eigenvalues (real – stability, pure imaginary – exponential instability or complex – oscillatory instability) depends on the values of the matrix elements and, consequently, on the parameters ( ). The eigenvalue problem is solved numerically, and the corresponding results are subsequently presented. The evolution of the stable and unstable vortices is obtained through direct numerical simulations of the dynamic Equation (2).
). The eigenvalue problem is solved numerically, and the corresponding results are subsequently presented. The evolution of the stable and unstable vortices is obtained through direct numerical simulations of the dynamic Equation (2).
Results and discussion
Two cases exist in which the eigenvalue problem can be solved analytically: (a) linear vortices and (b) nonlinear MCF without a central core. In both cases, all eigenvalues and eigenfunctions of the system are calculated explicitly. In the linear system,  is Hermitian and, consequently, possesses only real eigenvalues both with and without a central core. In the case of a nonlinear vortex in MCF without a central core, the cumbersome but straightforward calculations lead to the following stability conditions.
is Hermitian and, consequently, possesses only real eigenvalues both with and without a central core. In the case of a nonlinear vortex in MCF without a central core, the cumbersome but straightforward calculations lead to the following stability conditions.
The sufficient stability condition I when cos(α)≤0 is

where index j denotes different eigenvalues (j = 0, …, M – 1), and p is an integer. This equation gives the following sets of stable vortices with unlimited power: for S = 1, stable M = 3, 4; for S = 2, stable M = 3, 4, 5, 6, 7, 8; for S = 3, stable M = 4, 5, 6, 7, 8, 9, 10, 11, 12; for S = 4, stable M = 3, 6, 7, …, 16, and so on.
The sufficient stability condition II when  is
is

This equation gives the following sets of stable vortices in the low power region: for S = 1, stable M = 5, 6, 7,…; for S = 2, stable M = 9, 10,…; for S = 3, stable M = 3, 13, 14,…; for S = 4, stable M = 4, 5, 17, 18,…; and so on.
The numerical modeling demonstrates excellent agreement with the analytical results. Figure 2 summarizes the results of the linear stability analysis for the MCF with and without the central core. Without a loss of generality, we consider β0 = β1 = 1 and γ0 = γ1 = 1.
Schematic of the stability regions for vortices with topological charge S = 1 (a), S = 2 (b), S = 3 (c), and S = 4 (d) with respect to the number of cores in the MCF system. The green and blue bars in the plots denote the parameter areas with stable vortices in the MCF with and without a central core, respectively.
The general conclusion is that the MCF without a central core can support stable propagation of the discrete vortices with unlimited power for some values of parameters S and M. The obtained results are consistent with the findings in the Refs. 34,35, which predicted stable propagation of vortex structures with S = 1 and 2 in different two-dimensional lattice configurations. The presence of the central core enables the coupling of the perturbations in the periphery cores, and the interactions of the cores produce instability. The result is the creation of an instability window for some intermediate vortex powers, but there is no effect on stability at high powers.
The vortices with S = 1 and a small number of periphery cores, M = 3 and M = 4, are stable in the entire existence region (see Figure 2a). An important feature of the stable vortices is that vortex power is not bounded from above. The corresponding phase differences between neighboring periphery cores are α = 2π/3 and 2π/2, respectively. By increasing the number of periphery cores, M, the stability region of the vortices shrinks toward the low power vortices with P < 5. The presence of the central core for M = 3 opens the instability window 0 < P < 7.6, which does not affect the stability at high powers.
For S = 2, the stable vortices are for M = 3, …, 8, as observed in Figure 2b. The addition of a new periphery core destabilizes the vortices and produces instability windows for M = 3, 4, 5, 6. However, the vortices for M = 7 and M = 8 remain stable in the entire existence region.
In the stability window for S = 3, vortices covers the existence region for the vortex in the MCF with M = 4 characterized by the phase difference between neighboring periphery cores 3π/2, as observed in Figure 2c. By adding a new core in the periphery, the instability island appears and survives up to M = 9 after which the island disappears; similarly, for M = 10, 11, 12, the stability and existence region overlap. These vortices are characterized by the phase 3π/5, 6π/11, and π/2, respectively. The possibility of transferring high energy by S = 3 vortices in the certain parameter range is confirmed.
The phase change between adjacent cores given by 2πS/M = 8π/M for the S = 4 vortices is shown to stabilize the vortices in the MCF with 6 ≤ M ≤ 16, as observed in Figure 2d. Actually, the total overlap between the existence and stability region is found for M = 13 to M = 16 with the phase difference between neighboring periphery cores 8π/13, 4π/7, 8π/15, π/2, whereas for M = 6 to M = 12, the narrow instability island (also found for S = 3) exists. Above the critical value of M = 16, the vortices with S = 4 are unstable.
The eigenvalue spectrum of the vortices with an even number of cores contains complex eigenvalues with finite real parts, which determine the oscillatory instability of the vortex. Vortices with an odd number of cores possess both purely real and complex eigenvalues with finite real parts in the eigenvalue spectrum. In this spectrum, the development of instability is controlled by the eigenvalue with the greatest real part. All of these findings are based on the analytically and numerically developed linear stability analysis and are confirmed through dynamic analysis performed using direct numerical simulation of the model equations.
Figures 3 and 4 illustrate examples of the evolution of stable and unstable vortices obtained through direct numerical simulations. The developing instability is followed by the active inclusion of the central core in the energy redistribution of the system and the destruction of the vortex phase pattern. This phenomenon is shown in Figure 3 by comparing the phase diagrams of the central and periphery cores for the stable and unstable vortices with S = 2 and M = 4. The energy redistribution between the periphery and the central core is related to the destruction of the limit circle in the periphery core phase plot (Re(Aj) vs. Im(Aj), j = 1, …, M). As a consequence of the instability, the vortex structure evolves into a breathing mode with a more complex internal structure. Figure 3e and h illustrates this statement by increasing the complexity of the amplitude spectra in the case of the unstable vortex. The figures also indicate that the energy redistribution during the propagation of the unstable vortex is associated with decoherence in the MCF system, as Figure 4 schematically illustrates. A detailed consideration of the developing vortex instability is outside the primary scope of this study, which is focused on preserving stable coherent energy transmission through the MCF using vortex structures.
The eigenvalues(EVs) spectrum for S = 2 and M = 4 vortices. Plots (a), (b), and (c) show the phase plots of the central core amplitude; plots (d), (e), and (f) show the phase plots of the periphery core amplitude; and plots (g), (h), and (i) show the corresponding amplitude spectra. Plots (a), (d), and (g) with stable vortex P = 16.2, μ = –7.1 belong to stability region 1 (dashed line); plots (b), (e), and (h) with unstable vortex P = 24.2, μ = –11.1 belong to the instability region (dashed line in the instability region – gray region); and plots (c), (f), and (i) with stable vortex P = 58, μ = –28 belong to stability region 2 (dashed line).
In particular, our results indicate the possibility of the stable and coherent propagation of vortices with high power for a certain relation between the topological charge, S, and the number of periphery cores, M. The existence of vortex and stability regions overlap near the parameter ratio S/M = 1/4 for all vortex types. The presence of the central core (both linear and nonlinear) supports the development of instability and brings a new degree of freedom to the system. This new degree of freedom acts as an energy channel that provides for the energy exchange in the system that destabilizes the vortex structure. Only vortices with a particular phase ratio remain robust and maintain an unchanged energy distribution among the periphery cores. The most significant finding is the possibility of a stable and coherent transfer of high energy through the nonlinear MCF. Direct numerical simulations demonstrate that stable vortices remain robust and preserve coherence when subject to small amplitude and phase perturbations and small variations of the coupling constants.
Conclusions
In conclusion, we examined the formation, stability, and dynamical properties of the discrete vortex structures in interacting nonlinear MCF systems with one central and several periphery cores. Although nonlinearity generally tends to destabilize vortices, the coherent propagation of steady nonlinear vortices with high power is possible in a certain region of the parameter space. The most robust nonlinear vortices are observed for S = 1 and M = 4, which corresponds to a phase difference between neighboring periphery cores of α = π/2. The presence of a central core provides greater possibilities for instability to develop, which results in the creation of instability windows for certain intermediate vortex powers but does not affect the stability at high powers. The demonstrated remarkable feature of the stable vortex propagation carrying high optical power and preserving the orbital angular momentum has significant potential for many applications. These results can be used to develop a new model of orbital angular momentum multiplexing and high capacity transmission lines using MCF. The considered discrete optical vortices also have the potential for high power field trapping and transfer in MCF, which provides a method to manage and control the nonlinearity and to design new type of switches59, sources of high brightness coherent radiation or uniform light sources with tailored phase profiles. Moreover, an intriguing extension of this work is to generate and manage spatiotemporal vortex light bullets in MCF settings46,47,48,49.
References
Pismen LM . Vortices in Nonlinear Fields, International Series of Monographs in Physics 100. Oxford: Oxford Science, 1999.
Ahronov Y, Bohm D . Significance of electromagnetic potentials in the quantum theory. Phys Rev 1959; 115: 485–491.
Berry MV . Quantal phase factors accompanying adiabatic changes. Proc Roy Soc Lond A 1984; 392: 45–57.
Desyatnikov A, Kivshar Y, Torner L . Optical vortices and vortex solitons. Prog Opt 2005; 47: 291–391.
Pampaloni E, Ramazza PL, Residori S, Arecchi FT . Two-dimensional crystals and quasicrystals in nonlinear optics. Phys Rev Lett 1995; 74: 258–261.
Taranenko VB, Weiss CO, Stolz W . Semiconductor resonator solitons above bandgap. J Opt Soc Am B 2002;19: 684–688.
White AG, Smith CP, Heckenberg NR, Rubinsztein-Dunlop H, McDuff R et al. Interferometric measurements of phase singularities in the output of a visible laser. J Modern Opt 1991; 38: 2531–2541.
Nye JF, Berry MV . Dislocations in wave trains. Proc Roy Soc Lond A 1974; 336: 165–190.
Nye JF . Natural Focusing and Fine Structure of Light: Caustics and Wave Dislocations. Bristol: Institute of Physics Publishing, 1999.
Rozas D, Law CT, Swartzlander GA Jr . Propagation dynamics of optical vortices. JOSA B 1997; 14: 3054–3065.
Alexeyev CN, Volyar AV, Yavorsky MA . Linear azimuthons in circular fiber arrays and optical angular momentum of discrete optical vortices. Phys Rev A 2009; 80: 063821.
Allen L, Beijersbergen MW, Spreeuw RJ, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gausian laser modes. Phys Rev A 1992; 45: 8185–8189.
Allen L, Padgett MJ, Babiker M . The orbital angular momentum of light. Prog Opt 1999; 39: 291–372.
Bekshaev A, Soskin M, Vasnetsov M . Paraxial Light Beams with Angular Momentum. New York: Nova Publishers, 2008.
Gahagan KT, Swartzlander GA . Optical vortex trapping of particles. Opt Lett 1996; 21: 827–829.
He H, Friese MEJ, Heckenberg NR, Rubinsztein-Dunlop H . Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys Rev Lett 1995; 75: 826–829.
Garcés-Chávez V, Volke-Sepulveda K, Chávez-Cerda S, Sibbett W, Dholakia K . Transfer of orbital angular momentum to an optically trapped low-index particle. Phys Rev A 2002; 66: 063402.
Agrawal GS, Banerji J . Spatial coherence and information entropy in optical vortex fields. Opt Lett 2002; 27: 800–802.
Gibson G, Courtial J, Padgett M, Vasnetsov M, Pas'co V et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt Express 2004; 12: 5448.
Bouchal Z, Čelechovský R . Mixed vortex states of light as information carriers. New J Phys 2004; 6: 131.
Lee JH, Foo G, Johnson EG, Swartzlander GA . Experimental verification of an optical vortex coronagraph. Phys Rev Lett 2006; 97: 053901.
Swartzlander GA Jr, Ford EL, Abdul-Malik RS, Close LM, Peters MA et al. Astronomical demonstration of an optical vortex coronagraph. Opt Express 2008; 16: 10200–10207.
Tamburini F, Anzolin G, Umbriaco G, Bianchini A, Barbieri C . Overcoming the Rayleigh criterion limit with optical vortices. Phys Rev Lett 2006; 97: 163903.
Spektor B, Normatov A, Shamir J . Singular beam microscopy. Appl Opt 2008; 47: A78–A87.
Friese MEJ, Rubinsztein-Dunlop H, Gold J, Hagberg P, Hanstorp D . Optically driven micromachine elements. Appl Phys Lett 2001; 78: 547–549.
Turitsyn SK, Mezentsev VK, Dubov M, Rubenchik AM, Fedoruk MP et al. Sub-critical regime of femtosecond inscription. Opt Express 2007; 15: 14750–14764.
Sigler A, Malomed BA, Skryabin DV . Localized states in a triangular set of linearly coupled complex Ginzburg-Landau equations. Phys Rev E 2006; 74: 066604.
Mejía-Cortės C, Soto-Crespo JM, Vicencio RA, Molina MI . Vortex solitons of the discrete Ginzburg-Landau equation. Phys Rev A 2011; 83: 043837.
Desyatnikov A, Denz C, Kivshar Y . Nonlinear optical beams carrying phase dislocations. J Opt A, Pure Appl Opt 2004; 6: S209–S212.
Lopez-Aguayo S, Desyatnikov AS, Kivshar YS, Skupin S, Krolikowski W et al. Stable rotating dipole solitons in nonlocal optical media. Opt Lett 2006; 31: 1100–1102.
Leykam D, Malomed B, Desyatnikov AS . Composite vortices in nonlinear circular waveguide arrays. J Opt 2013; 15: 044016.
Malomed BA, Kevrekidis PG . Discrete vortex solitons. Phys Rev E 2001; 64: 026601.
Kevrekidis PG, Malomed BA, Gaididei YB . Solitons in triangular and honeycomb dynamical lattices with the cubic nonlinearity. Phys Rev E 2002; 66: 016609.
Pelinovsky DE, Kevrekidis PG, Frantzeskakis DJ . Persistence and stability of discrete vortices in nonlinear Schrödinger lattices. Physica D 2005; 212: 20–53.
Kevrekidis PG, Frantzeskakis DJ . Stabilizing the discrete vortex of topological charge S=2. Phys Rev E 2005; 72: 016606.
Fleischer JW, Bartal G, Cohen O, Manela O, Segev M et al. Observation of vortex-ring discrete solitons in 2D photonic lattices. Phys Rev Lett 2004; 92: 123904.
Neshev DN, Alexander TJ, Ostrovskaya EA, Kivshar YuS, Martin H et al. Observation of discrete vortex solitons in optically induced photonic lattices. Phys Rev Lett 2004; 92: 123903.
Desyatnikov AS, Kivshar YS . Rotating optical soliton clusters. Phys Rev Lett 2002; 88: 053901.
Ferrando A, Zacarés M, García-March MÁ, Monsoriu JA, De Córdoba PF . Vortex transmutation. Phys Rev Lett 2005; 95: 123901.
Soskin MS, Gorshkov VN, Vasnetsov MV, Malos JT, Heckenberg NR . Topological charge and angular momentum of light beams carrying optical vortices. Phys Rev A 1997; 56: 4064–4075.
Luther-Davies B, Christou J, Tikhonenko V, Kivshar YS . Optical vortex solitons: experiment versus theory. J Opt Soc Am B 1997; 14: 3045–3053.
Khonina SN, Kazanskiy NL, Soifer VA . Optical Vortices in a Fiber: Mode Division Multiplexing and Multimode Self-Imaging, Recent Progress in Optical Fiber Research (Edited by Yasin M, Harun SW, Arof H ). Rijeka: INTECH, 2012.
Malomed BA, Mihalache D, Wise F, Torner L . Spatiotemporal optical solitons. J Opt B 2005; 7: R53–R72.
Mihalache D . Linear and nonlinear light bullets: recent theoretical and experimental studies. Rom J Phys 2012; 57: 352–371.
Aceves AB, De Angelis C, Rubenchik AM, Turitsyn SK . Multidimensional solitons in fiber arrays. Opt Lett 1994; 19: 329–331.
Leblond H, Malomed BA, Mihalache D . Spatiotemporal vortices in optical fiber bundles. Phys Rev A 2008; 77: 063804.
Leblond H, Malomed BA, Mihalache D . Spatiotemporal vortex solitons in hexagonal arrays of waveguides. Phys Rev A 2011; 83: 063825.
Eilenberger F, Prater K, Minardi S, Geiss R, Röpke U et al. Observation of discrete, vortex light bullets. Phys Rev X 2013; 3: 041031.
Bozinovic N, Golowich S, Kristensen P, Ramachandran S . Control of orbital angular momentum of light with optical fibers. Opt Lett 2012; 37: 2451–2453.
Chan FYM, Lau AP, Tam HY . Mode coupling dynamics and communication strategies for multi-core fiber Systems. Opt Express 2012; 20: 4548–4563.
Zhu B, Taunay TF, Yan MF, Fini JM, Fishteyn M et al. Seven-core multicore fiber transmissions for passive optical network. Opt Express 2010; 18: 11117–11122.
Shalaby BM, Kermène V, Pagnoux D, Desfarges-Berthelemot A, Barthélémy A et al. 19-cores Yb-fiber laser with mode selection for improved beam brightness. App Phys B: Lasers Opt 2010; 100: 859–864.
Turitsyn SK, Rubenchik AM, Fedoruk MP, Tkachenko E . Coherent propagation and energy transfer in low-dimension nonlinear arrays. Phys Rev A 2012; 86: 031804
Rubenchik AM, Tkachenko EV, Fedoruk MP, Turitsyn SK . Power-controlled phase-matching and instability of CW propagation in multicore optical fibers with a central core. Opt Lett 2013; 38: 4232–4235.
Hizandis K, Droulias S, Tsopelas I, Efremidis NK, Christodoulides DN . Centrally coupled circular array of optical waveguides: the existence of stable steady-state continuous waves and breathing modes. Physica Scripta 2004; T107: 13–19.
Hizandis K, Droulias S, Tsopelas I, Efremidis NK, Christodoulides DN . Localized modes in a circular array of coupled nonlinear optical waveguides. Int J Bifurcat Chaos 2006; 16: 1739–1752.
Golshani M, Weimann S, Jafari Kh, Khazaei Nezhad M, Langari A et al. Impact of loss on the wave dynamics in photonic waveguide lattices. Phys Rev Lett 2014; 113: 123903.
Maluckov A, Hadžievski Lj, Malomed BA, Salasnich L . Solitons in the discrete nonpolynomial Schrödinger equation. Phys Rev A 2008; 78: 013616.
Desyatnikov AS, Dennis MR, Ferrando A . All-optical discrete vortex switch. Phys Rev A 2011; 83: 063822.
Acknowledgements
We acknowledge the financial support of the Engineering and Physical Sciences Research Council (project UNLOC), a grant from the Ministry of Education and Science of the Russian Federation (Agreement No. 14.B25.31.0003) and the Ministry of Education, Science and Technology Development, Serbia (Project III45010). The work was partly performed under the auspices of the U.S. Department of Energy at the Lawrence Livermore National Laboratory under Contract DE-AC52-08NA28752.
Note: Accepted article preview online 9 April 2015
Author information
Authors and Affiliations
Corresponding author
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications' website .
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permissing from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Hadžievski, L., Maluckov, A., Rubenchik, A. et al. Stable optical vortices in nonlinear multicore fibers. Light Sci Appl 4, e314 (2015). https://doi.org/10.1038/lsa.2015.87
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2015.87
Keywords
This article is cited by
-
Optical vortices in waveguides with discrete and continuous rotational symmetry
Journal of the European Optical Society-Rapid Publications (2021)
-
Su-Schrieffer-Heeger chain with one pair of \(\mathcal{P}\mathcal{T}\)-symmetric defects
Scientific Reports (2017)
-
Use of polarization freedom beyond polarization-division multiplexing to support high-speed and spectral-efficient data transmission
Light: Science & Applications (2016)