Abstract
The application of three-dimensional (3D) plasmonic nanostructures as metamaterials (MMs), nano-antennas, and other devices faces challenges in producing metallic nanostructures with easily definable orientations, sophisticated shapes, and smooth surfaces that are operational in the optical regime and beyond. Here, we demonstrate that complex 3D nanostructures can be readily achieved with focused-ion-beam irradiation-induced folding and examine the optical characteristics of plasmonic “nanograter” structures that are composed of free-standing Au films. These 3D nanostructures exhibit interesting 3D hybridization in current flows and exhibit unusual and well-scalable Fano resonances at wavelengths ranging from 1.6 to 6.4 µm. Upon the introduction of liquids of various refractive indices to the structures, a strong dependence of the Fano resonance is observed, with spectral sensitivities of 1400 nm and 2040 nm per refractive index unit under figures of merit of 35.0 and 12.5, respectively, for low-order and high-order resonance in the near-infrared region. This work indicates the exciting, increasing relevance of similarly constructed 3D free-standing nanostructures in the research and development of photonics and MMs.
Similar content being viewed by others
Introduction
Metamaterials (MMs) have been the subject of enormous research effort in recent years. Fascinating optical properties, such as negative index1,2,3, super-resolution4,5,6,7, and electromagnetic invisibility8,9, have been explored in three-dimensional (3D) MMs, many of these properties are based on plasmonic resonances. Fano resonances in plasmonic nanostructures and MMs, as highlighted recently by Luk’yanchuk and co-workers10, may have applications in sensors, lasing, switching, and nonlinear devices due to the steep profile of the resonance spectra. For example, Wu et al. demonstrated the application of a Fano-resonant asymmetric MM structure in ultrasensitive spectroscopy and the identification of molecular monolayers11. Chen et al. theoretically described an “extraordinary Fano resonance” with right-handedness in a right-handed polarization gap of compound spiral photonic crystals12. More recently, Wei et al. investigated weak Fano resonances in 3D dual cut-wire pairs13.
The key motivation in producing 3D structures has always been the realization of MMs with effective constituent properties that can be tuned in all propagation directions at various frequencies. Techniques for fabricating millimeter-scale 3D MMs that are operational in the microwave regime, such as split ring resonators (SRRs) and metal wires, are well established1. By comparison, scaling down 3D MMs for applications at higher frequencies, such as in the infrared and visible regimes, remains an active focus of research. Many micro/nano fabrication techniques featuring 3D structures that could be applied to photonic and MMs have been developed in recent years. These techniques include layer-by-layer stacking3,14,15, structural rolling16,17, shadow evaporation18, multilayer electroplating19, membrane projection lithography20,21, stress-driven assembly22, direct laser writing8,23,24,25,26,27,28, and ion-beam irradiation29,30,31. However, effective fabrication of nanoscale 3D plasmonic structures that can be spatially oriented with a hierarchical geometry remains challenging. In addition, most of the 3D MMs structures require supporting substrates, which may introduce undesirable effects. Theoretical studies have indicated that the substrate may have profound effects on the intrinsic properties of 3D MMs32 and frequently should be avoided. The emergence of focused-ion-beam (FIB) folding of metallic cantilevers33 offers a convenient method for constructing self-supporting nanostructures, but studies of FIB-fabricated two-dimensional (2D) arrays of 3D plasmonic elements and their optical characteristics have been limited.
In this article, we report the application of FIB folding for the direct fabrication of substrate-free 3D plasmonic nanostructures and their unusual Fano resonances. The fabrication process employs FIB nano-patterning combined with in situ irradiation-induced folding of metallic thin-film structures. We demonstrate that this method can be used to produce complex 3D structural elements with ease and is also feasible for the production of 2D arrays of millimeter-sized 3D elements, which have practical uses in many optical applications. Focus is given to a 2D array of a delicate structure (named as MH-VSRR) that consists of vertical U-shape split ring resonators (VSRRs) standing along an edge of rectangular metallic holes (MHs, i.e., subwavelength rectangular holes in a free-standing Au film). Because the MH-VSRR structures resemble a cheese grater, they are simply referred to as U-type “nanograters” in the following content. The MH-VSRR structures exhibit unusual Fano resonances under light excitation with an electric field polarized perpendicular to the SRR plane (U-plane), which is an unconventional polarized excitation scheme that cannot induce any resonance of a single SRR. The Fano resonance is highly sensitive to the refractive index of the surrounding medium, with a sensitivity of 2040 nm per refractive index unit (RIU) in the near-infrared (NIR) region, with potential applications in high-performance plasmonic sensing.
Materials and methods
Preparation of the self-supporting Au film
Si wafers were cleaned with acetone, alcohol and deionized water. The wafers were then spin-coated with a 1.2 µm layer of S1813 photoresist, followed by baking at 115 °C for 2 min and deposition of a gold film with a thickness of 80 nm using magnetron sputtering. The samples were then immersed in acetone for 24 h to fully dissolve the resist and obtain the suspended Au film. Finally, a transmission electron microscope copper grid was dipped into the solution to pick up the released film and dried in N2 in a clean room environment to obtain a flat and self-supporting Au film.
FIB nano-patterning and folding
An FIB system (FEI Helios 600i) was used for ion-beam nano-patterning and ion irradiation-induced folding. The acceleration voltage of Ga+ was 30 kV. An ion-beam current of 40 pA was used for the present work. Sophisticated patterns were pre-designed, and the milling and line-scanning irradiation-induced folding were performed automatically using the software of the FIB system.
Optical measurements
Transmission spectra were measured using a ×36, 0.5 numerical aperture reflective objective lens on an optical microscope (Hyperion 2000) coupled to a Fourier-transform infrared spectrometer (Vertex 70, Bruker) through a 40 µm × 40 µm spatial aperture. A homemade aperture was inserted after the reflective objective to confine the illumination cone with a conical angle of 5°, and the samples were tilted correspondingly to obtain normal incidence during measurement. The transmission spectra were calibrated using air (holes of the grid) as a reference. Refractive index sensing experiments were carefully conducted by immersing the samples very slowly into liquid oil with different refractive indices (Cargille Labs), and optical measurements were performed after the samples were stabilized. After the optical measurements, the oil was thoroughly removed by immersing the sample into sufficient acetone solution. The spectra of the cleaned structures were examined to confirm that no obvious changes had occurred compared with the spectra measured before oil immersion. Thus, we concluded that mild immersion of the structures in oil did not affect the inclined angle of the VSRR during the measurements.
Numerical simulations
The transmission spectra and electric/magnetic-field distributions were simulated by the finite-difference time-domain (FDTD) method. The electric/magnetic fields were calculated in planes 5 nm above the metal surface. The current distributions were simulated using the commercial software package CST Microwave Studio based on the finite integration method. We used realistic parameters describing gold’s lossy properties, with an electric conductivity of 4.561 × 107 S m−1. The surface current distributions were obtained using an H-field/surface current monitor.
Results and discussion
Fabrication of spatially oriented 3D nanostructures by FIB patterning and folding
A schematic of the 3D nanofabrication process we used to construct complex substrate-free 3D plasmonic nanostructures is presented in Figure 1. The process involved three main steps. The first step was the preparation of thin metallic films (e.g., Au), which were then isolated and transferred to a macroscopic grid. A thin metal film was first deposited onto a substrate that had been previously coated with a layer of photoresist (Figure 1a). The photoresist was then dissolved in acetone to release the film (Figure 1b), and the floating film was transferred onto a copper grid (Figure 1c–1d). The second step was the nano-patterning of the freely suspended thin metal film by FIB milling. Desirable patterns were produced with a sufficient ion dose so that they could be cut off, leaving only one edge of the individual shapes connected to the main film (Figure 1e). The third step was the controlled in situ spatial folding of the in-plane cantilever nanostructures by FIB irradiation. The third step, as the defining feature of this technique, must be delicately managed and will be further discussed below.
Schematic diagrams illustrating the steps in the fabrication of spatially oriented 3D nanostructures. (a) The gold thin film deposited on the photoresist-coated Si substrate. (b) The floating Au film after the photoresist was dissolved. (c) The Cu grid with a mesh area of 100 µm × 100 μm. (d) The Au thin film on the Cu grid obtained after film transfer. (e) 2D nano-patterns formed by FIB milling on suspended Au films. (f) Spatially oriented 3D nanostructures realized by in situ FIB irradiation-induced folding.
Figure 2 presents the ion-beam irradiation-induced folding of in-plane Au film cantilevers. The line-scanning strategy employed (namely, continuous scanning of the ion-beam spot along a nominally zero-width line passing across the base of an Au cantilever at normal incidence), as illustrated in Figure 2a, is intended to fold the cantilever to a desirable angle without cutting it off the main film. The bending process is believed to be driven mainly by the ion-implantation-induced stress at the area of ion-beam bombardment33,34,35. Figure 2b shows the folding process of the Au film cantilevers as a function of the ion dose. The folding angle θ (defined as depicted in the inset of Figure 2c) was almost linearly proportional to the ion-beam dose used and eventually reached a saturated value. A maximum value of 90° was achievable when the ion beam was applied normal to the film. These results indicate that the FIB technique using a combination of direct nano-patterning and in situ ion-beam irradiation-induced folding is capable of fabricating spatially oriented 3D nanostructures with a reasonably good degree of control and reproducibility.
Ion-beam irradiation-induced folding of in-plane Au nanostructures. (a) Illustration of the line-scanning strategy. (b) SEM images of folded cantilevers. (c) The folding angle (θ) as a function of the ion dose. The Au nano “fins” are 80 nm thick, 5.0 μm long and 1.0 μm wide. (d–g) SEM images of various spatially oriented 3D nanostructures: (d) staircase-like structures; (e) a composite U-shape structure; (f) boxes with U-shaped walls; (g) boxes with U-shaped holes on the walls. Scale bars: 1 µm. SEM, scanning electron microscope.
A high degree of flexibility is also required for an effective fabrication process. To demonstrate that this method provides such flexibility, several types of Au film 3D nanostructures are selectively presented in Figure 2. In addition to vertical Au nano “fins” (with a width of 2.0 µm and an aspect ratio larger than 10), Au stripes were formed in a segmented style by judicious selection of the line-scanning sequence. With the advantage of the flexible patterning capability of the FIB, sophisticated hierarchical micron/nanostructures were constructed with the advantage of the flexible patterning capability of the FIB, as shown in Figure 2d and 2e. For practical applications, another advantage of this 3D nanofabrication approach is that 3D structures can be prepared with high consistency across a sufficiently large area, e.g., on the order of square millimeters, with a manageable processing time using a step-repeat patterning strategy (see part I of Supplementary Information). Figure 2f and 2g presents some typical 3D structures obtained by the method to illustrate the ability to fabricate large, complex arrays. Overall, the technique of combining direct FIB nano-patterning and in situ ion-beam irradiation-induced folding offers good flexibility, spatial resolution, and the necessary precision for the fabrication of complex 3D nanostructure arrays.
Unusual Fano resonances of MH-VSRR arrays
The results presented above illustrate that FIB nano-patterning and in situ irradiation-induced folding can be used in a practical manner to fabricate a different class of 3D plasmonic structures, referred to as nanograters, that are spatially oriented and substrate free. The optical characteristics of nanograters have not been reported. As a typical demonstration, we now focus on arrays of MH-VSRRs, i.e., the U-type nanograters (Figure 3a–3c), which exhibit rather unusual Fano resonances under a less well-explored experimental configuration.
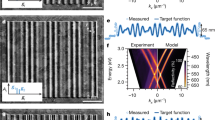
Fano resonances from vertical U-shaped SRRs standing along horizontal rectangular hole arrays in a free-standing metallic film (MH-VSRRs). (a) Schematic of the MH-VSRR structure. (b, c), SEM images of the fabricated MH-VSRRs, with h = 1.2 µm, l = 1.0 µm, w = 340 nm, ax = ay = 2.0 µm and px = py = 3.0 µm. (d, e), As-measured transmission spectra of the MH-VSRRs shown in c under normal incidence with the electric field polarized along the x- and y-direction, respectively. Normal incidence is employed throughout this work. The gray spectral region at approximately 4.2 µm is a high-absorption region from CO2 in the FTIR chamber and was omitted for clear comparison with simulations. (f, g), Simulated transmission spectra of the MH-VSRRs corresponding to d and e, respectively. The corresponding spectra of rectangular hole arrays in metallic films (MHs) in the absence of VSRRs are also plotted for comparison in Figure 3d–3g. FTIR, Fourier transform infrared spectroscopy.
U-shape SRRs have been popular and widely accepted as building blocks for various 2D and 3D MMs3,14,19,36,37,38,39. Conventionally, the resonances of an SRR can be excited by incident light with the electric field (E) polarized parallel to the U-plane (for instance, along the x-direction as shown in Figure 3a) or, alternatively, with the magnetic field perpendicular to the U-plane36,40. Therefore, in SRRs reported thus far, including planar36,40, vertical41,42, and multilayered3,14 SRR structures, an unconventional excitation scheme in which the electric field is polarized perpendicular to the U-plane in the y-direction would normally induce no electromagnetic resonance and hence has usually remained unexplored. Here, we demonstrate that under such unconventional excitation of the MH-VSRRs, the integration of SRRs significantly changes the extraordinary optical transmission (EOT)43 properties of the original MH arrays. A maximum value of the absolute transmission efficiency (calculated by dividing the fraction of light transmitted by the fraction of surface area occupied by the holes) of approximately 1.8 has been achieved. As shown in Figure 3e, clear Fano-type asymmetric line shapes were observed at both low and high frequencies under unconventional excitation, with Fano asymmetry factors of q = 0.86 and −0.14, respectively (see part II of Supplementary Information). By contrast, the influence of SRR structures on the transmission spectra under the conventional polarized excitation scheme (with the electric field polarized along the x-direction) appeared to be relatively weak (Figure 3d). These observations were further confirmed by numerical simulations using a 3D FDTD method, as shown in Figure 3f–3g. Fano resonances exhibit asymmetric and steep characteristics due to the interference between a spectrally overlapping broad resonance or continuum and a narrow discrete resonance10. As clearly shown in Figure 3d and 3e, the “broad” resonance can be attributed to the EOT background continuum from the array of MHs. However, the “narrow” resonance appears to be unexpected because the SRRs would not support any resonance under such an unconventional excitation scheme in the absence of MHs36,40, indicating the unusual nature of the observed Fano resonances.
To identify the mechanism underlying the observed Fano resonance behavior, U-type nanograters of MH-VSRR arrays with various heights h, i.e., the vertical U-arm length, were fabricated and investigated. As shown in Figure 4a, the Fano resonance dips shifted toward longer wavelength as the height of the VSRRs increased, consistent with the results of the simulations (Figure 4b) and confirming the crucial influence of the VSRRs. Further systematic simulation results demonstrated that the wavelength of the high-order resonance dip was mainly related to h, while the position of the low-order resonance dip increased linearly with increasing h, decreasing l and increasing ay, where l and ay are also geometric parameters as defined in Figure 3a (see also part III of Supplementary Information for further details). Moreover, as shown in Figure 4c, the experimental measurements of samples of different geometrical parameters also indicated that the wavelength of the low-order resonance dip maintains a nearly linear relationship with an “empirical length” (EL), which is defined as EL = h + (ax-l)/ 2 + ay/ 2.
Fano resonances from MH-VSRRs in mid-infrared. (a, b), measured and calculated transmission spectra of the MH-VSRRs under normal - incidence with the electric field polarized along the y-direction and parameters of l = 0.9 µm, w = 250 nm, ax = ay = 2.0 µm and px = py = 3.0 µm. The gray spectral region at approximately 4.2 µm is a high-absorption region from CO2 in the FTIR chamber. (c) The wavelength of the low-order resonance dip as a function of the empirical length (EL, defined as EL = h + (ax-l)/ 2 + ay/ 2). (d, e), Simulated current distributions of the sample at the low-order and high-order resonance dips in b with h = 1.48 µm. The 3D current flow routes are schematically indicated by the arrows. The amplitude distributions of the electric field in the xz and xy planes are plotted below the corresponding plot of the current distributions. The monitored xz and xy planes are 5 nm away from the front surface of the MHs and the top surface of the VSRRs, respectively. The number in each figure indicates the maximum value of the electric field enhancement.
To further evaluate this trend, the current distributions of the sample at the resonance dips (Figure 4d and 4e) were simulated using CST Microwave Studio. As illustrated in Figure 4d, the current flow at the low-order resonance dip exhibited a 3D-like route, which is fundamentally different from the traditional multi-planar 3D MMs operating on multi-planar 2D current flows. Obviously, this 3D current is a hybridized current flowing between VSRRs and MHs units, and the length of its route is identical to the EL. This hybridized current is also evident in the calculated electric field distributions at the bottom of Figure 4d, in which the locations of the maximum electric field match well with the two ends of the 3D current flow. Therefore, our measurements and calculations (using both CST and FDTD) consistently demonstrate that the 3D hybridization in current flow is responsible for the generation of low-order Fano resonance, which can be induced by electromagnetic excitation under a y-polarized electric field (please also refer to part IV of Supplementary Information). By comparison, the current flow at the high-order resonance dip exhibited an anti-phase current flow simply along the arms of the VSRRs with respect to the current flow of MHs in the xy plane, as shown in Figure 4e. Therefore, the resonance induced by this current flow is a relative local effect and is more dependent on the length of the VSRR arms than on other geometrical parameters. This conclusion is also supported by the calculated electric field distribution shown in Figure 4e and the simulation results for the geometrical dependence of the resonance dips (shown in part III of Supplementary Information). The presence of 3D hybridizations in current flow associated with both low-order and high-order Fano resonances has not been reported for any traditional 3D MMs and appears to be unique to the 3D MH-VSRR structures. A geometrical change from 3D MH-VSRRs toward 2D plasmonic structures could result in significant degradation of the Fano resonance properties (see part V of Supplementary Information), indicating the critical importance of the 3D features. Their potential in applications such as plasmonic sensing and imaging11 has yet to be explored.
As a further example, the FIB fabrication method was pushed closer to the facility resolution limit to fabricate nanograters of the MH-VSRR type on a 50-nm-thick Au film with a repeating unit of 750 nm, as shown in Figure 5a. The Fano resonances of the nanograter structures exhibited very good scaling behavior (indicated by the arrow in Figure 4c) and strong resonances in the NIR (Figure 5b) and present well-preserved resonance shapes compared with their mid-infrared counterparts (Figure 3e).
Scaled-down MH-VSRRs with Fano resonances in the NIR and ultra-sensitive refractive index-sensing properties. (a) SEM images of the fabricated structures with parameters of h = 560 nm, l = 430 nm, w = 150 nm, ax = ay = 560 nm and px = py = 750 nm. Inset, the top view of an MH-VSRR. Scale bar: 500 nm. (b) Measured transmission spectra of the MH-VSRRs in air and oil with a refractive index of 1.300 ± 0.0002, respectively. Spectra are smoothed for clarity. The low-order and high-order Fano resonance dips exhibit spectral shifts with refractive index sensitivities of 2040 and 1400 nm RIU−1, respectively. (c) The measured transmission spectra of the MH-VSRRs in oil with refractive indices of 1.300 and 1.320, respectively. (d) The wavelengths of the low-order and high-order Fano resonance dips as a function of the refractive index of the surrounding medium. The solid lines are linear fits of the data; the corresponding slopes are indicated.
The NIR MH-VSRR samples were subsequently immersed in index matching oils with different refractive indices (Cargille Labs). As shown in Figure 5b, the figure of merit (FOM) values, which equal the refractive index sensitivities divided by the resonance linewidth, were 12.5 and 35 for the low-order and high-order resonances, respectively. The low-order Fano resonance dip shifted from 1.620 µm in air to 2.233 µm in oil with a refractive index of 1.300 ± 0.0002. In Figure 5c, oil with a refractive index of 1.320 ± 0.0002 was also employed to verify the resolution capability of the nanograter; a slight difference in the refractive index as small as 0.02 was recognized. The relationship between the resonance dip wavelength and refractive index is shown in Figure 5d, presenting the refractive index sensitivity, which is the change in the resonance dip wavelength per RIU. The sensitivity was 2040 nm RIU−1 for the low-order resonance. The high-order Fano resonance dip had a refractive index sensitivity of 1400 nm RIU−1. Both the refractive index sensitivity and FOM values observed in this work appear to be the highest among reported SRR structures in the NIR42,44.
These large sensitivities of the U-type plasmonic nanograters are likely the result of multiple factors. First, the Fano resonance itself is intrinsically sensitive to environment38. Second, the free-standing MH-VSRRs were completely exposed to the surrounding environment, which may have significantly enhanced the sensitivity of the Fano resonances due to the increased effective sensing volume42. Third, compared with the planar SRR structures, the unique 3D hybridization in current flows of MH-VSRRs may also contribute to the observed behavior due to the 3D distribution of the electric field.
Conclusions
In conclusion, we have demonstrated that the combination of FIB direct nano-patterning and in situ ion-beam-induced folding can be effectively used to fabricate spatially oriented complex 3D nanostructures over a large surface area on self-supporting thin metallic films. The method is particularly suitable for the production of various plasmonic nanograter structures. The present work focused on U-type plasmonic nanograters consisting of an array of vertical U-shape split-ring resonator patterns standing along an edge of horizontal subwavelength rectangular holes. The 3D plasmonic nanostructures exhibited scalable unusual Fano resonances characterized by the 3D hybridization of current flows under an unconventional polarized excitation experimental geometry. The Fano resonances of the free-standing U-type nanograters exhibited a very strong dependence on the refractive index of the surrounding medium, with a refractive index sensitivity as high as 2040 nm RIU−1 in the NIR. These experimental observations illustrate that the local modifications to the phase and amplitude of the light wave front on a subwavelength scale induced by the nanograter structures profoundly influence the propagation of the incoming light, thereby suggesting that such nanostructures may be applied in a wide range of optical applications, including high-performance plasmonic sensing. Although studies are underway to examine the optical characteristics of hierarchical nanograter structures, the present work appears to indicate an exciting relevance of these nanostructures fabricated by the FIB-based technique to photonics and MMs, which may lead to new advances in these research fields. The proposed spatially oriented 3D nanostructures, which exhibit unique bending and folding features, may also possess novel mechanical responses and thus could potentially find applications in optomechanics, pressure sensing, and temperature monitoring in nanoscale dimensions.
References
Shelby RA, Smith DR, Schultz S . Experimental verification of a negative index of refraction. Science 2001; 292: 77–79.
Valentine J, Zhang S, Zentgraf T, Ulin-Avila E, Genov DA et al. Three-dimensional optical metamaterial with a negative refractive index. Nature 2008; 455: 376–379.
Liu N, Guo H, Fu L, Kaiser S, Schweizer H et al. Three-dimensional photonic metamaterials at optical frequencies. Nat Mater 2008; 7: 31–37.
Smolyaninov II, Hung YJ, Davis CC . Magnifying superlens in the visible frequency range. Science 2007; 315: 1699–1701.
Pendry JB . Negative refraction makes a perfect lens. Phys Rev Lett 2000; 85: 3966–3969.
Liu Z, Lee H, Xiong Y, Sun C, Zhang X . Far-field optical hyperlens magnifying sub-diffraction-limited Objects. Science 2007; 315: 1686.
Liu Z, Durant S, Lee H, Pikus Y, Fang N et al. Far-field optical superlens. Nano Lett 2007; 7: 403–408.
Ergin T, Stenger N, Brenner P, Pendry JB, Wegener M . Three-dimensional invisibility cloak at optical wavelengths. Science 2010; 328: 337–339.
Schurig D, Mock JJ, Justice BJ, Cummer SA, Pendry JB et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006; 314: 977–980.
Luk’yanchuk B, Zheludev NI, Maier SA, Halas NJ, Nordlander P et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat Mater 2010; 9: 707–715.
Wu C, Khanikaev AB, Adato R, Arju N, Yanik AA et al. Fano-resonant asymmetric metamaterials for ultrasensitive spectroscopy and identification of molecular monolayers. Nat Mater 2012; 11: 69–75.
Chen WJ, Lee JC, Dong JW, Qiu CW, Wang HZ . Fano resonance of three-dimensional spiral photonic crystals: paradoxical transmission and polarization gap. Appl Phys Lett 2011; 98: 081116.
Wei X, Altissimo M, Davis TJ, Mulvaney P . Fano resonances in three-dimensional dual cut-wire pairs. Nanoscale 2014; 6: 5372–5377.
Liu N, Liu H, Zhu S, Giessen H . Stereometamaterials. Nat Photon 2009; 3: 157–162.
Liu N, Hentschel M, Weiss T, Alivisatos AP, Giessen H . Three-dimensional plasmon rulers. Science 2011; 332: 1407–1410.
Chen Z, Mohsen R, Gong Y, Chong CT, Hong M . Realization of variable three-dimensional terahertz metamaterial tubes for passive resonance tunability. Adv Mater 2012; 24: OP143–OP147.
Huang FM, Sinha JK, Gibbons N, Bartlett PN, Baumberg JJ . Direct assembly of three-dimensional mesh plasmonic rolls. Appl Phys Lett 2012; 100: 193107.
Zhang S, Fan WJ, Minhas BK, Frauenglass A, Malloy KJ et al. Midinfrared resonant magnetic nanostructures exhibiting a negative permeability. Phys Rev Lett 2005; 94: 037402.
Fan K, Strikwerda AC, Tao H, Zhang X, Averitt RD . Stand-up magnetic metamaterials at terahertz frequencies. Opt Express 2011; 19: 12619–12627.
Burckel DB, Wendt JR, Ten Eyck GA, Ellis AR, Brener I et al. Fabrication of 3D metamaterial resonators using self-aligned membrane projection lithography. Adv Mater 2010; 22: 3171–3175.
Burckel DB, Wendt JR, Ten Eyck GA, Ginn JC, Ellis AR et al. Micrometer-scale cubic unit cell 3D metamaterial layers. Adv Mater 2010; 22: 5053–5057.
Chen CC, Hsiao CT, Sun S, Yang KY, Wu PC et al. Fabrication of three dimensional split ring resonators by stress-driven assembly method. Opt Express 2012; 20: 9415–9420.
Rill MS, Plet C, Thiel M, Staude I, von Freymann G et al. Photonic metamaterials by direct laser writing and silver chemical vapour deposition. Nat Mater 2008; 7: 543–546.
Gansel JK, Thiel M, Rill MS, Decker M, Bade K et al. Gold helix photonic metamaterial as broadband circular polarizer. Science 2009; 325: 1513–1515.
Thiel M, Rill MS, von Freymann G, Wegener M . Three-dimensional bi-chiral photonic crystals. Adv Mater 2009; 21: 4680–4682.
Lu WE, Zhang YL, Zheng ML, Jia YP, Liu J et al. Femtosecond direct laser writing of gold nanostructures by ionic liquid assisted multiphoton photoreduction. Opt Mater Express 2013; 3: 1660–1673.
Tanaka T, Ishikawa A, Kawata S . Two-photon-induced reduction of metal ions for fabricating three-dimensional electrically conductive metallic microstructure. Appl Phys Lett 2006; 88: 081107.
Cao YY, Takeyasu N, Tanaka T, Duan XM, Kawata S . 3D metallic nanostructure fabrication by surfactant-assisted multiphoton-induced reduction. Small 2009; 5: 1144–1148.
Cui A, Li W, Luo Q, Liu Z, Gu C . Freestanding nanostructures for three-dimensional superconducting nanodevices. Appl Phys Lett 2012; 100: 143106.
Cui A, Li W, Luo Q, Liu Z, Gu C . Controllable three dimensional deformation of platinum nanopillars by focused-ion-beam irradiation. Microelectron Eng 2012; 98: 409–413.
Cui A, Fenton JC, Li W, Shen TH, Liu Z et al. Ion-beam-induced bending of freestanding amorphous nanowires: The importance of the substrate material and charging. Appl Phys Lett 2013; 102: 213112.
Zhao RK, Koschny T, Soukoulis CM . Chiral metamaterials: retrieval of the effective parameters with and without substrate. Opt Express 2010; 18: 14553–14567.
Rajput NS, Banerjee A, Verma HC . Electron- and ion-beam-induced maneuvering of nanostructures: phenomenon and applications. Nanotechnology 2011; 22: 485302.
Arora WJ, Smith HI, Barbastathis G . Membrane folding by ion implantation induced stress to fabricate three-dimensional nanostructures. Microelectron Eng 2007; 84: 1454–1458.
Arora WJ, Sijbrandij S, Stern L, Notte J, Smith HI et al. Membrane folding by helium ion implantation for three-dimensional device fabrication. J Vac Sci Technol B 2007; 25: 2184–2187.
Katsarakis N, Koschny T, Kafesaki M, Economou EN, Soukoulis CM . Electric coupling to the magnetic resonance of split ring resonators. Appl Phys Lett 2004; 84: 2943–2945.
Xiong X, Jiang SC, Hu YH, Peng RW, Wang M . Structured metal film as a perfect absorber. Adv Mater 2013; 25: 3994–4000.
Xiong X, Xue ZH, Meng C, Jiang SC, Hu YH et al. Polarization-dependent perfect absorbers/reflectors based on a three-dimensional metamaterial. Phys Rev B 2013; 88: 115105.
Kuznetsov AI, Miroshnichenko AE, Fu YH, Viswanathan V, Rahmani M et al. Split-ball resonator as a three-dimensional analogue of planar split-rings. Nat Commun 2014; 5: 3104.
Tatartschuk E, Shamonina E, Solymar L . Plasmonic excitations in metallic nanoparticles: resonances, dispersion characteristics and near-field patterns. Opt Express 2009; 17: 8447–8460.
Chen WT, Chen CJ, Wu PC, Sun SL, Zhou L et al. Optical magnetic response in three-dimensional metamaterial of upright plasmonic meta-molecules. Opt Express 2011; 19: 12837–12842.
Wu PC, Sun G, Chen WT, Yang KY, Huang YW et al. Vertical split-ring resonator based nanoplasmonic sensor. Appl Phys Lett 2014; 105: 033105.
Ebbesen TW, Lezec HJ, Ghaemi HF, Thio T, Wolff PA . Extraordinary optical transmission through sub-wavelength hole arrays. Nature 1998; 391: 667–669.
Pryce IM, Kelaita YA, Aydin K, Atwater HA . Compliant metamaterials for resonantly enhanced infrared absorption spectroscopy and refractive index sensing. ACS Nano 2011; 5: 8167–8174.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under grant nos. 91123004, 61390503, 61475186 and 91023041, and XDB07020200 and by the Technical Talent Program of the Chinese Academy of Sciences. The authors thank AD Boardman at University of Salford, DP Tsai and YW Huang at Taiwan University for simulating discussions.
Note: Accepted article preview online 31 March 2015
Author information
Authors and Affiliations
Corresponding authors
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications' website.
Supplementary information
Rights and permissions
This license allows readers to copy, distribute and transmit the Contribution- as long as it attributed back to the author. Readers are permitted to alter, transform or build upon the Contribution as long as the resulting work is then distributed under this is a similar license. Readers are not permitted to use the Contribution for commercial purposes. Please read the full license for further details at - http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Cui, A., Liu, Z., Li, J. et al. Directly patterned substrate-free plasmonic “nanograter” structures with unusual Fano resonances. Light Sci Appl 4, e308 (2015). https://doi.org/10.1038/lsa.2015.81
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2015.81
Keywords
This article is cited by
-
Ultrafast all-optical switching in a silicon-polymer compound slotted photonic crystal nanobeam cavity
Optical Review (2023)
-
Three-dimensional nanoprinting via charged aerosol jets
Nature (2021)
-
Fano resonance Rabi splitting of surface plasmons
Scientific Reports (2017)
-
Metamaterial study of quasi-three-dimensional bowtie nanoantennas at visible wavelengths
Scientific Reports (2017)