Introduction

Metasurfaces (also known as planar metamaterials or metafilms) are a special low-dimensional class of artificially structured media. This class is represented by thin metal films and surfaces periodically patterned on a sub-wavelength scale, which can be readily fabricated using the existing planar technologies. Apart from their spectral selectivity1 metasurfaces have demonstrated intriguing electromagnetic effects such as asymmetric transmission2,3 and optical activity without structural chirality4. They can exhibit resonant dispersion mimicking electromagnetically induced transparency and the slow-light phenomenon5,6,7, be invisible8, efficiently convert polarization9,10,11, or perfectly absorb radiation12,13. Metasurfaces with gradient structuring anomalously reflect and refract light10,11,12,13,14,15 and can act as lenses, wave-plates, and diffraction gratings16,17,12,13. Planar metamaterials are also able to enhance the light–matter interaction facilitating sensing20, energy harvesting21, and generation of coherent radiation22,23.

The functionality of the most common types of planar metamaterials is determined by the individual resonant response of their basic structural elements – metamolecules, which are only weakly coupled to each other. When electromagnetic coupling between the metamolecules is strong24 the relative phase of their excitation becomes important and the resulting spectral response is no longer determined by the individual resonances of the metamolecules. The metamaterial spectrum is then shaped by the collective, spatially coherent modes of metamolecular excitations that engage a large ensemble of metamolecules25. The introduction of structural disorder in such an ensemble reduces the degree of coherency and leads to the weakening and broadening of its collective resonant response, which might be seen to vanish at even moderate levels of the disorder24,26. Strong inter-metamolecular coupling is also responsible for the ‘size effect’ where the resonant transmission band of a metamaterial narrows with increasing size of the metamaterial sample27.

In this paper we show that strong inter-metamolecular coupling can lead to a new phenomenon of ‘tunnel vision’, which renders a coherent metasurface transparent within a very narrow range of light propagation directions. This effect is accompanied by ‘rectification’ of incident wavefronts, when initially spherical waves emerge as planar while traversing such a metasurface in the absence of any spatial phase modulation or adaptive feedback28. The transmitted wavefronts appear parallel to the plane of the metamaterial and the effect does not depend on the curvature of the incident wavefronts.

As illustrated in Figure 1, such response is fundamentally different from that of conventional convex lenses and recently demonstrated metasurface-based lenses16,19. Indeed, a lens introduces a spatially dependent delay in the optical path, which compensates the curvature of the incident spherical wavefront if its source is located in the ‘focal spot’ of the lens. In a convex glass lens, for example, the spatial variation of optical delay is achieved by gradually reducing the thickness of the lens towards its edges (see Figure 1a). In a metasurface-based lens the same is accomplished by changing the size and/or shape of its metamolecules: the resulting position-dependent phase lag for light scattered by the metamolecules mimics spatial variation of optical delay in the glass lens (see Figure 1b). For spherical waves originating at its focal point, the lens converts the entire range of incident wavevectors into a much narrower range that converges around the optical axis of the lens.

Figure 1
figure 1

Three ways of producing planar wavefronts with a point light source.

Full size image

The ‘tunnel vision’ effect can be understood as wavevector filtering, which occurs in a narrow transparency window of the metasurface corresponding to the collective resonance of its strongly coupled metamolecules. Indeed, in a regular planar array of identical metamolecules with the sub-wavelength period d the coupling is strongest when the metamolecules are excited by a normally incident plane wave, i.e. they all oscillate in-phase. Any plane wave with its k-vector deviating from the array’s normal (so that k|| ≠ 0) introduces a phase delay in the excitation of the metamolecules that linearly varies along the metasurface. The resulting de-phasing reduces the strength of coupling through the factor cos(k|| d) and hence changes the energy of the collective mode (see Supplementary Information). Consequently, the transparency window shifts to a different frequency and the metasurface becomes opaque. Operating at the frequency of its collective resonance the structure therefore acts as a wavevector selective surface (WSS): it admits only plane waves with k-vectors parallel (or nearly parallel) to its normal, while all other waves are reflected back and/or absorbed (see Figure 1c).

Materials and Methods

Modeling

The propagation of spherical wavefronts through a wavevector selective surface was simulated using a 3D Maxwell’s equations solver of the COMSOL Multiphysics simulation package 3.5a (COMSOL, Inc., Burlington, USA). The metasurface was modeled as a 14 × 14 array of asymmetrically split rings (ASRs) with the period d = 565 μm. The rings had the radius r = 245 μm and were split into wire sections 140° and 160° long separated by equal gaps. The wire sections had the width of 40 μm and were modeled as perfect electric conductors. The thickness of the supporting substrate was 120 μm and its permittivity was assumed to be ε = 2.2. The size of the simulation domain allocated for the transmitted wavefronts was 7910 × 7910 × 7910 μm.

Experiment

The metamaterial sample had been fabricated by etching a 9-μm-thick copper layer covering one side of a 120-μm-thick low-loss teflon substrate and closely resembled the modeled split-ring array both in terms of its size and design parameters. The transmitted wavefronts were visualized in the 0.12–0.23 THz range of frequencies using a state-of-the-art THz-field imaging technique29, which enabled mapping of the electric-field component of the propagating waves with the spatial resolution of 160 μm and frequency resolution of 0.01 THz. The spherical waves were produced by illuminating a pinhole placed 500 μm away from the sample with a focused THz beam polarized parallel to the split of the rings. The diameter of the pinhole was 1750 μm, which ensured adequate signal-to-noise ratio for the wavefront imaging at low frequencies with signs of diffraction visible only above ∼0.2 THz.

Results and Discussion

As an example of WSS we consider here a planar metamaterial based on ASRs, a regular array of identical metamolecules formed by pairs of metallic arcs of different length (see inset to Figure 2a). For normally incident plane waves with the E-field being parallel to the split its transmission spectrum features a narrow asymmetric pass-band with a sharp roll-off (Fano resonance), which in our case is centered around ν0 = 0.165 THz (see Figure 2a). This spectral feature corresponds to the resonant excitation of anti-symmetric charge-current mode, the so-called trapped or sub-radiant mode30,31, where charges q and currents j induced in the opposite arcs of each ASR-metamolecule oscillate with equal amplitudes but opposite phases (see inset to Figure 2a). Such mode can be represented by a combination of an oscillating magnetic dipole with its moment being orthogonal to the metamaterial plane m = (0, 0, mz), and an electric quadrupole Q characterized by two non-zero in-plane components Qxy = Qyx. Being arranged in a 2D-lattice with a sub-wavelength unit cell these multipoles cannot contribute to the far-field scattering of the array when they oscillate in-phase: coherent superposition of their fields results in electromagnetic modes with the characteristic wavenumbers larger than 2π/λ0, and thus the multipole radiation by the array is trapped in the near-field zone. The absence of scattering in the far-field zone renders the metamaterial transparent, while the accumulation of energy in the spatially coherent surface waves ensures strong inter-metamolecular coupling27.

Figure 2
figure 2

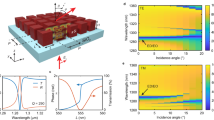
THz wavevector selective surface. (a) WSS transmission spectrum calculated for plane-wave illumination at normal incidence (solid curve), and 20° incidence with TM polarization (dashed curve). Gray shading indicates the slope of the trapped-mode resonance. Right inset shows a schematic of the WSS, a planar array of ASRs; left inset shows a fragment of the fabricated WSS sample. (b), (c) & (d) Angular spectra of the transmitted wavevectors calculated for spherical-wave illumination at 0.130, 0.164, and 0.229 THz, respectively

Full size image

For the ASR-metasurface, the effect of wavevector filtering is particularly pronounced near 0.165 THz, at the sharp edge of its transparency band where a small blue shift of the band translates into a strong reduction of the metamaterial transmission (see Figure 2a). Such a shift corresponds to an increase of the trapped-mode’s energy and therefore should result from the weakening of attractive inter-metamolecular coupling. In the array of ASR-metamolecules this coupling is mediated by electric quadrupole–quadrupole interaction, and at oblique incidence it is affected by the TM-component of the plane wave (see Supplementary Information).

We first demonstrated the effect of wavevector filtering numerically, by simulating the propagation of spherical waves with a large wavefront curvature through the ASR-metasurface (see Figure 3a–3c). The waves were produced by an electromagnetic point source placed close to the metasurface, at a distance equal to just one period of the ASR-array, d, and polarized parallel to the split of the rings. The transmitted waves are visualized through the spatial variation of their phase and are presented for three characteristic frequencies ν0 (as indicated in Figure 2a), which correspond to identical levels of transmission at the edges of the stop-band (ν0 = 0.130 THz and 0.229 THz) and at the pass-band (ν0 = 0.164 THz). As evident from Figure 3a and 3c, the curvature of the wavefronts at 0.130 and 0.229 THz remains practically unperturbed upon propagation through the metasurface. The situation changes markedly at the trapped-mode resonance, where the transmitted wavefront emerges nearly planar signifying thus the regime of wavevector filtering (see Figure 3b).

Figure 3
figure 3

Wavefront transformation by ASR-based wavevector selective surface. (a-c) Modeled spatial variations of the instantaneous phase, which visualize the wavefronts transmitted by the WSS at 0.130, 0.164 and 0.229 THz when it is illuminated by spherical waves. The waves originate from a vertically polarized point source/pinhole (not shown), on the left of the shaded purple bars, which represent the cross-section of the WSS. (d-f) Spatial-frequency spectra of the wavefronts shown in panels (a-c) respectively. For clarity, the images of the spectra were enhanced by removing background noise. (g-i) Experimentally measured spatial variation of the instantaneous phase, which visualizes the wavefront of the initially spherical waves transmitted by the WSS at 0.13, 0.16, and 0.23 THz. (j-l) Spatial-frequency spectra of the wavefront patterns shown in panels (g-i), correspondingly. For clarity, the images of the spectra were enhanced by removing background noise.

Full size image

To characterize the response of the ASR-metasurface in terms of the transmitted k-vectors, i.e. partial plane-wave components, we plotted the spatial-frequency spectrum of the transmitted wavefront (see Figure 3d–3f). A perfectly spherical wave would have been represented by a circle of radius k0 = 2π ν0/c corresponding to the fundamental spatial frequency, as indicated by the doted circles in Figure 3d–3f. Clearly, at ν0 = 0.130 THz and ν0 = 0.229 THz the spatial-frequency spectra have the form of partial concentric circles. The inner circle has a radius of k0 and corresponds to the fundamental spatial frequency of the wavefront pattern. The outer circles represent higher harmonics 2k0, 3k0 etc. that are present due to unharmonic (‘saw’-like) phase variations between 0 and 2π. Given the extent of the circular patterns, the angles of incidence for the admitted partial plane-wave components fall in the relatively wide range from –60° to +60°, which in our case is limited by the size of the modeled array. The amplitudes of the partial waves and therefore their relative contributions to the resulting wavefronts show little variation with the incidence angle, as evident from the angular spectra of the k0-component presented in Figure 2b and 2d. Thus, the response of the metasurface off the trapped-mode resonance is only weakly sensitive to the direction of the incident wavevectors.

At ν0 = 0.164 THz, however, the spatial-frequency spectrum collapses along the horizontal axis indicating that the transmission of the metasurface becomes k-dependent and most of the wavevectors deviating from the structure’s normal are being rejected (see Figure 3e). This is also illustrated in Figure 2c, which shows that at ν0 = 0.164 THz the angular spectrum of the transmitted k0-component converges along the 0° direction within the (–25°, +25°) range of angles. The angular selectivity of the ASR-metasurface can be improved further by reducing its structural asymmetry, since the latter would increase the strength of coupling between the split-ring metamolecules30.

The effect of wavevector filtering has been confirmed also experimentally using a WSS-metamaterial sample that closely resembled the modeled ASR-array both in terms of its size and design parameters. The obtained images of the transmitted wavefronts are presented in Figure 3g–3i. Evidently, the patterns of the wavefronts, as well as their spatial-frequency spectra plotted in Figure 3j–3l show a very good agreement with our simulations. The appearance of noise in the phase data at 0.23 THz (and higher frequencies) coincides with the diffraction minima due to the finite size of the pinhole aperture. Additional experimental data, including the wavefront images obtained at other frequencies and their comparison with the results of our simulations can be found in Supplementary Information. Although the limited bandwidth of the spatial-frequency filtering might be an issue for some practical applications, this problem could be addressed by employing the so-called double-continuum Fano resonance approach32, where the bandwidth of the effect is increased by stacking 2D-chiral versions of the metamaterial (i.e. ASR structures lacking reflection symmetry)33 with adiabatically varied resonance frequency.

Unlike the wavevector manipulation performed by the lenses, the demonstrated principle of k-selectivity does not rely on gradient structuring. As a result, metamaterials with strong inter-metamolecular coupling can extract plane-wave components from arbitrary shaped wavefronts. A remote analogue of WSS functionality and the associated ‘tunnel vision’ effect might be found in conventional ray-optics systems such as astronomical telescopes: for the same magnification the telescopes with higher f-ratio (i.e. slower telescopes) will allow an observer to see stars and nebulas on a much darker background yielding overall higher contrast images. Such telescopes have smaller field of view, which limits the directions of the admitted light rays to those nearly parallel to the axis of the ‘tunnel’ (i.e. telescope) hence blocking most of the light scattered by the atmosphere and immediate surrounding.

Conclusions

In conclusion, we have shown that strong electromagnetic coupling among the basic structural elements of a planar metamaterial provides a new degree of freedom to light manipulation, leading to an intriguing effect of wavefront rectification and tunnel vision. The effect results in arbitrary-shaped wavefronts becoming planar as they traverse the plane of the metamaterial in the absence of any spatial phase modulation or adaptive feedback, and is demonstrated here both theoretically and experimentally in the THz part of the spectrum. The proposed concept of wavevector selective surfaces can have a number of unique applications. For example, WSSs can improve the characteristics of observational instruments by blocking stray light and therefore acting as a flat analogue of a lens hood; or by reducing the effect of light scattering emanating from the immediate surrounding, dew, dust or scratches. WSSs can be exploited for directional filtering in free-space communications in highly turbid or strongly scattering media, yielding an improved signal-to-noise ratio.