Abstract
We propose a new approach to the generation of an alphabet for secret key exchange relying on small variations in the cavity length of an ultralong fiber laser. This new concept is supported by experimental results showing how the radiofrequency spectrum of the laser can be exploited as a carrier to exchange information. The test bench for our proof of principle is a 50-km-long fiber laser linking two users, Alice and Bob, where each user can randomly add an extra 1-km-long segment of fiber. The choice of laser length is driven by two independent random binary values, which makes such length become itself a random variable. The security of key exchange is ensured whenever the two independent random choices lead to the same laser length and, hence, to the same free spectral range.
Similar content being viewed by others
Introduction
Fiber lasers are now well-developed and reliable devices used in a wide range of applications. As it occurs with other types of cavity resonators, the confinement of light within the optical cavity of a laser allows only a discrete number of longitudinal distributions of the electromagnetic field or cavity modes to build up. Such a filtering effect features a quasiperiodic frequency response (the exact periodicity being broken by the frequency dependence of the fiber refractive index): the frequency spacing between neighboring modes is referred to as the free spectral range (FSR) and scales inversely with the cavity length. Although in this work, we consider fiber laser cavities of a ring type using erbium-doped fibers (EDFs), our results can be extended to different laser architectures, which may also include free-space propagation sections provided that the overall gain exceeds the cavity losses.
Most of the EDF laser cavities studied so far are just a few tens of meters long, entailing a cavity mode spacing of a few megahertz. However, it has been demonstrated that the cavity length of a fiber laser can be extended to several hundreds of kilometers.1 This is not surprising in fact if one thinks how low the linear losses of optical fibers at telecommunication wavelengths are and how easily these can be compensated by lumped or distributed optical amplifiers. The feasibility of extending the laser cavity over the whole communication link connecting the two parties, forming an ultralong fiber laser (UFL), has raised groundbreaking possibilities in communications and particularly in secure communications. An innovative concept of a key distribution system based on an erbium-doped or Raman gain UFL has been recently proposed and demonstrated.2,3,4,5 In this scheme, each of the two users (conventionally called Alice and Bob) places a randomly chosen, spectrally selective mirror at his/her end of the fiber laser, with the two-mirror choice representing a key bit. The security in this scheme stems from lasing states that have lost distinguishability, from the perspective of a potential eavesdropper, because of their symmetry. The key is coordinated from dynamic changes of the laser Bragg reflectors and from lasing state characterization by the legitimate end users. As a classical scheme, very much like chaotic lasing in coupled lasers and algorithmic cryptography, an UFL scheme cannot be proven to be unconditionally secure (i.e., unbreakable), contrariwise to what ideal quantum key distribution schemes are believed to be. Instead, the UFL scheme prospective application offers a practical and secure key distribution system in which security is set from technological bounds. Further work is required in order to fully quantify the extent of security provided by the UFL concept. Nonetheless, such schemes offer a practical, reliable and highly secure alternative strategy for secret key exchange, requiring only readily available, low-cost standard fiber-optic components, and being particularly attractive in scenarios where long ranges and fast bit rates are required.
In this paper, we propose what is, to the extent of our knowledge, a completely new way of exchanging a secret key over an UFL link, which relies on random changes of the FSR of the laser cavity rather than on random changes of the cavity losses. Consequently, unlike the previously proposed UFL scheme, our laser is always above the lasing threshold, and operates in alternating rapid transient and steady-state modes keeping the same optical bandwidth. The key idea of our work is based on the simple observation that the FSR of a laser cavity can be used as an information carrier and, hence, processing the FSR traces can make the information bits available all along the cavity. For a cavity of tens of kilometer length scale, the FSR is only a few kilohertz wide. Measurement of the FSR can be performed, e.g., by a real-time analysis of the electrical signal supplied by a photodiode that detects one of the laser outputs. Hereafter, we will refer to this new key distribution protocol as a radiofrequency shifting key exchange (RFSKE). Specifically, in this scheme, the FSR of the laser cavity is switched between different values by simply adding or subtracting fiber segments of given lengths to or from the cavity. This can be easily implemented by using 1×N switches with N different optical fiber paths so to change the cavity length in a predesigned way. In our implementation, N=2, and two out of four possible combinations of cavity length choices give the same value of FSR, which entails the possibility of having an undetectable bit of information. Instead of a random insertion of optical bandpass filters (BPFs), here we use the natural periodic filtering effect of the cavity to tag the laser spectrum in a way that it carries the information bits itself.
Switching the cavity length of a laser is a known technique used in metrology for molecular diagnostics 6,7 or in frequency-shifted feedback lasers, where the cavity is modified during the course of time by an inline modulator.8,9 Note also incidentally that the idea of secret key exchange using a combination of short and long path lengths is reminiscent of a quantum cryptographic scheme known as the Franson interferometer.10 However, to the best of our knowledge, the concept of FSR coding for secret key exchange has not been considered in the context of UFL cryptography yet.
Materials and methods
Principle of operation
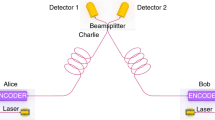
Figure 1 depicts a schematic of the UFL-based RFSKE system. The system consists of a bidirectional, 50-km-long ring fiber laser, in which in order to exchange a key bit, Alice and Bob independently choose to add a 1-km-long segment of fiber or leave the cavity length unchanged, with the corresponding indicator functions being ‘1’ and ‘0’, respectively. Thus, the laser has a random length determined by the combination of users' choices and taking on the values: 50 km (0,0 state), 51 km (0,1 or 1,0 state) and 52 km (1,1 state), and hence, random is also the FSR. A potential eavesdropper, Eve, measuring the FSR in the (0,0) or (1,1) state can easily infer the corresponding cavity length choices and therefore, the bits in these cases are rejected. However, in the (1,0) and (0,1) states leading both to the same FSR, Eve is unable to determine which user chose which length, thus rendering the key-bit exchange secure. Alice, knowing her own length choice, can determine the complementary choice of Bob, and vice versa. The two of them can therefore assign, for example, a logical ‘1’ to the (1,0) state and a logical ‘0’ to (0,1). Note that the conditional probability of the cavity length upon a given state is expected to be uniformly distributed, and this is ensured in our experiment by a software-driven pseudorandom number generator.
Experimental set-up
The two single-mode fiber drums in Figure 1 play the role of an existent public infrastructure. Each of the two bays, called Alice and Bob, provides two allowed access points to the bidirectional ring through 90/10 tap couplers with the terminals A1, A2, and B1, B2. Each bay has two 12-m-long segments of EDF that are core pumped by a 980-nm diode. The schematic in Figure 1 does not show that each diode pumps bidirectionally both EDF segments through a 50/50 fiber coupler at 980 nm so as to maintain the symmetry for clockwise and counterclockwise propagation in the ring. A 5-nm-wide optical BPF centered at the fixed wavelength of 1559 nm is placed in the middle of each bay. These filters only limit the spectral window in use and do not play any direct role in coding. The optical power at the laser output ports is approximately −11 dBm when the laser is operated slightly above threshold. A ceramic switch is placed close to each fixed filter. A transistor–transistor logic signal can reconfigure the laser by changing the state of the switch from bar to cross mode. In bar (0) mode, the switch simply connects the main input to the main output; in cross mode (1), the switch adds an extra propagation over 1 km of fiber in a ‘loop in loop’ set-up. A computer-generated random number is sent to a microprocessor unit (Arduino DUE) that controls the state of both switches via two logic level shifters. The detection of the laser output is ensured by a 1-GHz indium gallium arsenide photodiode connected to the analog input of the same microprocessor unit that provides a 12-bit analog to digital conversion. The numerical Fourier transform is then computed on the computer to obtain the FSR.
There are no polarization scrambling elements in our laser, and the whole set-up is not acoustically isolated from the laboratory environment. Further, we would like to note that the measurements in our experiment are carried out in a contrived laboratory setting rather than in a natural setting as reported in Ref. 11. The acoustic noise of the environment contributes to produce permanent random fluctuations of the instantaneous laser intensity. This important issue will be discussed elsewhere. We note, however, that our protocol of coding is based on shifting the radiofrequency spectrum of the laser rather than on instantaneous time-domain on–off keying. Incidentally, coding with frequency diversity in the presence of channel noise can be seen as an extension of the known technique of orthogonal frequency division multiplexing12 to ultralong laser communications.
Results and discussion
Experimental measurements
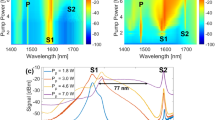
Figure 2 depicts the optical spectra of the laser for the four possible states as obtained from measurements taken close to the lasing threshold. The optical bandwidth of the laser is determined by a tradeoff between gain and losses in the cavity. To reduce the unavoidable irregularities in the spectra due to the different spectral responses of the switches at the different driving voltages, we included an additional tunable 100-GHz optical BPF into the laser cavity. This filter only makes the optical spectra more similar to each other and does not play any role in information coding. The laser system was on hold during the time of the optical spectrum analysis. A common feature of all spectral profiles is a sharp peak with a 3-dB width of 0.11 nm and located at 1560.5 nm. Importantly, the (0,1) and (1,0) states have closely similar spectra. This would make it difficult for Eve to deduce the states by measuring the optical spectrum.
Optical spectra of the UFL for the four states. Top panel: the black solid curve is for state (0,0); the red dashed curve is for state (1,1). Bottom panel: the blue solid curve is for state (0,1); the green dashed curve is for state (1,0). The laser central wavelength is 1560.5 nm and its 3-dB bandwidth is 0.11 nm. UFL, ultralong fiber laser.
The crucial point of the proposed RFSKE scheme lies in a fast detection of the FSR through the analysis of the electrical signal emitted by a photodiode. It is useful to recall here that the time-domain analysis of the intensity of a light field I(t) relies on the acquisition of the fourth-order correlation function of the field (see, e.g., Ref. 8). We note that a change in FSR originating in a change in cavity length is reflected by a slight frequency shift of a component or tone of the radiofrequency spectrum of the laser. Therefore, to shorten the acquisition time and/or to facilitate the reading of the laser states, one can inspect those tones that are located at frequencies multiple of the basic FSR: the higher the multiple order, the larger the tone's frequency shift. Because the laser radiofrequency spectrum takes the form of a frequency comb, when the frequency shift of a given tone exceeds the tone's bandwidth, the corresponding change in cavity length can easily be detected. Similarly to what happens in dual-comb spectroscopy, however, the frequency detuning being measured should not exceed half of the FSR.13 In our proof-of-principle experiment, we analyzed the electrical signal from the photodiode with a radiofrequency spectrum analyzer (the results are not shown in this paper), and we found that the FSR was approximately 4-kHz wide. By looking at the radiofrequencies close to 20 kHz, which represents a multiple of five of the FSR, we observed that a change of 2% in laser length (1 km) brings a frequency shift of 0.4 kHz, which is a multiple of five of a 2% change in FSR. This confirmed the point made above. The proposed RFSKE protocol enables one to write bits of information into physical hertz of the spectrum with an efficiency that can be higher than that of laser cryptographic systems based on a random hopping of the laser optical central wavelength.3 In our implementation of the scheme, the numerical Fourier transform replaces the more classical physical heterodyne beating to detect the hopping in central frequency arising from a change in cavity length. Since the state of the laser is stored in an equivalent radiofrequency bandwidth, with the RFSKE scheme, the available optical bandwidth can be fully utilized to make multiple pairs of users sharing a common fiber link and using different laser channels work in parallel.
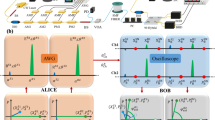
The buffer of our analog-to-digital converter has a size of 20 000 readings, corresponding to a temporal window of 20 ms. In principle, such a temporal window would allow for random generation and reading of 50 laser states per second, although one has to set apart some time for the laser transients (the round trip light time in the cavity is 0.24 ms). We tested the reliability of our coding/decoding process by randomly generating 2000 laser states and reading the electrical output signal from the photodiode. Figure 3 shows the collected data as Fourier transforms. Bright colors in the graph indicate likely situations. For ease of reading, the data are grouped in four sets, each being conditioned by one of the four possible random choices set by the computer. The data set conditioned by the choice of the (0,0) state clearly shows a persistence of the highest intensity around the frequency 20.4 kHz: the presence of a local maximum of intensity around this frequency can then be used as an indicator to identify the state. Similarly, the longest laser length used for the (1,1) state causes a contraction of the FSR and pinpoints the position of the fifth-order radiofrequency tone at 19.6 kHz. The bottom panels in Figure 3 show the results when the input states (1,0) and (0,1) are selected: in both cases the fifth-order radiofrequency tone is located at 20 kHz, thereby giving the two states the same radiofrequency signature. Alice and Bob can remove this ambiguity by tracing the operation modes of their switches. We also note that in the region of radiofrequency spectrum being studied, the frequency shifts of the spectral tones exceed the tone's bandwidths. This enables the implementation of a simple decision algorithm.
The decision step is also of critical importance for a fast evaluation of the FSR. Once the 20 000 samples were received and Fourier transformed, the strategy that we adopted to detect the FSR was again based on monitoring the fifth harmonic of the signal spectrum, as this proved to be effective in our case. We evaluated the spectral intensities p1, p2 and p3 of the signal I(t) at the respective frequencies 20.4 kHz, 20 kHz and 19.6 kHz, thereby generating a triplet of values (p1, p2, p3) for each data acquisition. The compliance bandwidth of the spectral profiles was 0.2 kHz. Each reading and signal processing operation can be represented as a point in the three-dimensional space of the (p1, p2, p3) parameters which plays the role of a constellation diagram, as shown in Figure 4. If p1>p2>p3, a decision is made in favor of the longest possible laser cavity (0,0 state). Similarly, the condition p1<p2<p3 identifies the shortest cavity (1,1 state). The two states (0,1) and (1,0) are in principle indistinguishable since they both attain the same frequency position, as also shown in Figure 3. In our measurements, we kept track of the random number generated by the computer so that an error occurred when a wrong decision was made. Two thousand laser states were generated randomly, and 98.95% of these were correctly detected. The results obtained are summarized in Figure 4. Different laser states are rendered with points of different colors by the random number generator: black indicates the (0,0) state, red is for the (1,1) state, blue is for (0,1) and green is for (1,0). The distinguishability of the symbols at the receiver is visualized in this constellation diagram by the net distinction among the point clouds of the same color (corresponding to the same switch settings). An error would be visualized in the diagram as a point of a different color from the surrounding cloud. The indistinguishability of the secure bit states from the perspective of an external eavesdropper is visualized by an overlap of the blue and green clouds: in this volumetric region the probability of Eve confusing the (0,1) state with the (1,0) state is very close to the ideal case of 50% (i.e., no knowledge of the key). Such a probability is drastically reduced for the legitimate users since they can keep track of their own random choice; this fact is represented in the diagram by the coexistence of the two color clouds in the same volume. We would like to note that the time-domain fluctuations of the laser induce changes of several orders of magnitude in the elements of the triplets, and such values are plotted on a logarithmic scale.
Limitation of current set-up and future perspectives
Figures 2 and 3 reveal that there are some residual differences between the (0,1) and (1,0) states in both the optical and the radiofrequency domains. These differences stem from the different light losses associated with the two states as well as from the different responses of the two switches. To counteract these problems, Alice and Bob could include additional ad hoc components into their set-ups. While the discussion of all available solutions is beyond the scope of this paper, Figure 2 highlights that a way to remove detectable differences in the optical spectra of the laser is to use in-cavity narrowband filtering.
In our scheme, the key exchange rate between Alice and Bob is fundamentally limited by the number of light round trips that are necessary to obtain a clear signature of the cavity modes - the exact number of required round trips may vary depending on the type of signal processing and/or optical amplification used. A way to obviate this problem would be to exploit the available optical bandwidth in full: with this in mind, we shifted the laser central wavelength from 1560.5 nm to 1560.7 nm (the results are not shown in this paper) by manually tuning the in-cavity narrowband optical filter. The 3-dB optical bandwidth of the laser was 0.06-nm wide at 1560.7 nm. We verified that at the new central wavelength, the corresponding radiofrequency spectrum still allowed the lasing states to be correctly detected with a 98% success rate: as expected, the RFSKE is independent of the optical bandwidth filled up by the laser. These results confirm the potential of extending the proposed RFSKE scheme to a parallel cascade laser configuration in which each of M lasers operates at a different central wavelength: Alice and Bob would then operate M subsystems centered at different wavelengths and connected to the common public network fiber by multiplexers/demultiplexers. The transmission speed would increase by a factor of M in such case. It is also worth noting here that, since Alice and Bob are in control of the active medium of the laser as well as of the frequency-dependent losses, they could differentiate clockwise and counterclockwise propagations in the ring cavity by using non-reciprocal devices such as circulators. At the same time, they could attenuate the lasing intensities artificially when they do not use the extra 1-km fiber loop. This way, Eve would not be able to extract the information of (0,1) and (1,0) states by monitoring the lasing intensities in both directions simultaneously.
In our experimental set-up, the optical losses associated with the bar and cross modes of the switches cannot be separately controlled, in particular the losses associated with the shortest cavity state of the laser cannot be increased. Different switching technologies, such as those based on fixed couplers and semiconductor or acousto-optic switches, or Mach-Zehnder modulators, could be considered as to improve the system operation.
Furthermore, a careful analysis of our system has revealed that the two switches used in this experiment do not completely reject either path. Consequently, when at least one of the switches is in cross mode, the radiofrequency spectrum of the laser features an additional periodicity of 185 kHz, which can be viewed as the effect of a nested (or compound) loop of approximate length 1.1 km.14 However, this fact does not compromise our proof of concept: we indeed managed to attain similar responses for the (0,1) and (1,0) states through fine tuning of the control voltage of the switches. Incidentally, this fact shows that a fraudulent addition of a nested loop to the system would modify the radiofrequency spectrum of the laser, and it would be unveiled by the (0,0) state in which neither Alice nor Bob use their extra fiber segment. Real-time monitoring of the radiofrequency spectrum extended to several orders of magnitude for frequency would be desirable to check the integrity of the link and strengthen the system's security.
In this experiment, the data reading and decision-making time was significantly longer than 20 ms since the microprocessing unit takes about 10 s to send data out to the computer. In other words, the data transmission process was longer than the laser transient caused by the switching between cavity lengths. This may temporarily spoil or degrade the signatures of the cavity modes by the signal I(t) due to the erratic presence of time-domain fluctuations, which may explain the observed 1%–2% error rate in the detection process. The laser transients could be made shorter by using a different optical amplification technology such as Raman or semiconductor amplification, or by using optical modulators. Note that optical modulators or frequency shifters may provide an alternative solution to the use of switches and an extra segment of fiber in the system's set-up. This principle has been already discussed in the context of lasers for molecular diagnostics in Refs. 6 and 7. In-cavity phase or frequency modulators could be used to obtain a fast varying spectrum,9 thereby confusing the optical detection by Eve. The use of polarization scramblers could further improve the system. Finally, the UFL–RFSKE scheme proposed in this paper could be implemented within a linear laser cavity configuration as well.
Conclusions
We have presented a new approach to secret key exchange for laser cryptography, and carried out a proof-of-principle demonstration of this new concept. We have experimentally demonstrated, we believe for the first time, how the radiofrequency spectrum of an UFL can be used to establish a secure communication between two parties. Although the demonstrated classical cryptographic scheme cannot ensure the same security level than that provided by idealized quantum key distribution systems, we believe that it represents an interesting tradeoff solution to enforce the security of communication systems beyond the standard software protocols and employing conventional, off-the-shelf components. Our results open up new avenues to studies involving non-traditional schemes for secure communications. In this paper, we have focused on the presentation of the basic concept and the implementation aspects of the new approach. A security analysis will be addressed in a future work. Furthermore, the radiofrequency monitoring of an UFL can be of interest for applications in diverse research fields, such as in distributed sensing.
References
Ania-Castañón JD, Ellingham TJ, Ibbotson R, Chen X, Zhang L et al. Ultralong Raman fiber lasers as virtually lossless optical media. Phys Rev Lett 2006; 96: 023902.
Scheuer J, Yariv A . Giant fiber lasers: a new paradigm for secure key distribution. Phys Rev Lett 2006; 97: 140502.
Zadok A, Scheuer J, Sendowski J, Yariv A . Secure key generation using an ultra-long fiber laser: transient analysis and experiment. Opt Express 2008; 16: 16680–16690.
Bar-Lev D, Scheuer J . Enhanced key-establishing rates and efficiencies in fiber laser key distribution systems. Phys Lett A 2009; 373: 4287–4296.
El-Taher A, Kotlicki O, Harper P, Turitsyn SK, Scheuer J . Secure key distribution over a 500 km long link using a Raman ultra-long fiber laser. Laser Photonics Rev 2014; 8: 436–442.
Brewer RG, Genack AZ . Optical coherent transients by laser frequency switching. Phys Rev Lett 1976; 36: 959–962.
Genack AZ, Brewer RG . Optical coherent transients by laser frequency switching. Phys Rev A 1978; 17: 1463–1474.
Yatsenko LP, Shore BW, Bergmann K . Coherence in the output spectrum of frequency shifted feedback lasers. Opt Commun 2009; 282: 300–309.
Krupa K, Bettenzana M, Tonello A, Modotto D, Manili G et al. Four-wave mixing in nonlinear fiber with two intracavity frequency-shifted laser pumps. IEEE Photonics Technol Lett 2012; 24: 258–260.
Franson JD . Bell inequality for position and time. Phys Rev Lett 1989; 62: 2205–2208.
Saito LA, de Souza EA . A comparison between in-field and in-laboratory 50 km ultralong erbium-doped fiber lasers actively mode-locked. Opt Express 2012; 20: 17001–17009.
Cimini LJ . Analysis and simulation of a digital mobile channel using orthogonal frequency division multiplexing. IEEE Trans Commun 1985; 33: 665–675.
Ideguchi T, Poisson A, Guelachvili G, Picqué N, Hänsch TW . Adaptive real-time dual-comb spectroscopy. Nat Commun 2014; 5: 3375.
Zhang J, Lit JW . Compound fiber ring resonator: theory. J Opt Soc Am A 1994; 11: 1867–1873.
Acknowledgements
This work was supported by the French National Research Agency (grants LABEX SIGMALIM and ANR 08-JCJC-0122 PARADHOQS), the European Research Council (project ULTRALASER), the Leverhulme Trust (grant RPG-278) and the Spanish MICINN project TEC2011-27314 (RAMAS). We also acknowledge support by the XLIM Institute (grant VIP2013).
Note: Accepted article preview online 27 January 2015
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This work is licensed under a Creative Commons Attribution 3.0 Unported License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
About this article
Cite this article
Tonello, A., Barthélémy, A., Krupa, K. et al. Secret key exchange in ultralong lasers by radiofrequency spectrum coding. Light Sci Appl 4, e276 (2015). https://doi.org/10.1038/lsa.2015.49
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2015.49
Keywords
This article is cited by
-
0.75 Gbit/s high-speed classical key distribution with mode-shift keying chaos synchronization of Fabry–Perot lasers
Light: Science & Applications (2021)
-
Encryption key distribution via chaos synchronization
Scientific Reports (2017)