Abstract
We propose theoretically and demonstrate experimentally the generation of light pulses whose polarization varies temporally to cover selected areas of the Poincaré sphere with both tunable swirling speed and total duration (1 ps and 10 ps, respectively, in our implementation). The effect relies on the Rabi oscillations of two polariton polarized fields excited by two counter-polarized and delayed pulses. The superposition of the oscillating fields result in the precession of the Stokes vector of the emitted light while polariton lifetime imbalance results in its drift from a circle of controllable radius on the Poincaré sphere to a single point at long times. The positioning of the initial circle and final point allows to engineer the type of polarization spanning, including a full sweeping of the Poincaré sphere. The universality and simplicity of the scheme should allow for the deployment of time-varying full-Poincaré polarization fields in a variety of platforms, timescales, and regimes.
Similar content being viewed by others
Introduction
A new dimension has been literally opened for the control and manipulation of light with “polarization shaping”1,2. This makes the most out of the vectorial nature of light by determining its time evolution not only in phase and amplitude but also in its state of polarization. Since the interaction of light and matter is polarization sensitive, the control of this additional degree of freedom has allowed to outbeat the performances of light in many of its usual applications, e.g., providing optimized photon ionization3, sub-wavelength localization4, or timing with zeptosecond precision5. Proposals abound as to its future applications in both a classical and quantum context6. Beyond the extension of the concept of pulse shaping to encompass polarization, there has been as well increasing demand for time-independent but spatially varying polarization beams7 such as cylindrical vector beams8. When providing all the states of polarization to realize so-called “full Poincaré beams”9, these also demonstrate advantages in similar endeavors, such as boosted scattering or sub-wavelength localization9. They also allow direct industrial applications in laser micro-processing, such as improving the efficiency and quality of processes like drilling holes for fuel-injection nozzles10, processing of silicon wafers11, or the machining of medical stent devices12. A new chapter of optics with fundamental as well as applied benefits has therefore been started with the availability of beams with a nontrivial dynamics of polarization.
Here, we propose a mechanism that brings together these two twists on polarized light, by providing (i) full Poincaré beams, (ii) in time. The underlying principle relies on an ubiquitous feature of light–matter interaction, Rabi oscillations13, and as such is platform-independent and can be realized in both the classical (normal mode coupling) and quantum regimes14. We demonstrate experimentally the mechanism in a semiconductor microcavity15 in strong exciton–photon coupling16. This proof-of-principle realization of a new type of light, taking all the states of polarization in the time duration of each pulse, opens the way to the deployment of time-varying polarization fields in a wide variety of platforms, timescales, and regimes of operations. It can also be generalized to non-optical systems.
Materials and methods
Theoretical model
The effect is based on the coherent superposition of fields of different polarizations, each in the regime of Rabi oscillations17. One is, therefore, in presence of four fields: two light-fields in a state of polarization, say left (↺) and right (↻) circularly polarized, each Rabi oscillating with a matter-field of corresponding polarization. Fields of different polarization are not coupled. In the linear regime in which the effect takes place, the system is thus described by four complex amplitudes αp and βp with p = ↺, ↻ the state of polarization of the photon α and matter β fields. In our case the matter field is excitonic. In the quantum regime, these amplitudes describe a probability for quantum states  , with a determined number i of photons and j of excitons in the polarization p, with wavefunction
, with a determined number i of photons and j of excitons in the polarization p, with wavefunction  (q being orthogonal to p). In the classical regime, on the other hand, these same variables describe directly the amplitude and phase of the electromagnetic components of the light. While in the latter case, one does not require a quantum formalism per se, it can be cast in this form as well introducing the coherent states,
(q being orthogonal to p). In the classical regime, on the other hand, these same variables describe directly the amplitude and phase of the electromagnetic components of the light. While in the latter case, one does not require a quantum formalism per se, it can be cast in this form as well introducing the coherent states,  , in which case the state of the four fields is described by the wavefunction
, in which case the state of the four fields is described by the wavefunction  , which features no quantum superposition or any other quantum effect. In the classical regime, the state is instead written in any of the familiar forms to represent polarization, such as Stokes or Jones vectors. In terms of the latter, the state of polarization reads:
, which features no quantum superposition or any other quantum effect. In the classical regime, the state is instead written in any of the familiar forms to represent polarization, such as Stokes or Jones vectors. In terms of the latter, the state of polarization reads:

The reason to cast the classical version also in a quantum formalism is two-fold: first it allows a more general treatment unifying both regimes, only with different interpretations for the variables α, β which nevertheless obey the same equations. Second, even in the classical regime, as is the case of our experiments below, some features such as incoherent pumping and dephasing are more conveniently tackled in the formalism of open quantum systems than with a statistical theory of classical electromagnetism. In the quantum formalism, the dynamics of the fields, uncoupled in polarization, is simply described with the Hamiltonian  for the ladder operators ap (for the photon) and bp (exciton), with g the coupling strength, at resonance and in the rotating frame. This light-matter coupling gives rise to the two new modes of the system, the upper,
for the ladder operators ap (for the photon) and bp (exciton), with g the coupling strength, at resonance and in the rotating frame. This light-matter coupling gives rise to the two new modes of the system, the upper,  , and the lower,
, and the lower,  , polaritons, respectively. One can then straightforwardly obtain the intensity
, polaritons, respectively. One can then straightforwardly obtain the intensity  of the photons emitted by the system, in any basis, and the degree of polarization
of the photons emitted by the system, in any basis, and the degree of polarization  through the relationships
through the relationships  ,
,  and
and  in the quantum formalism or, equivalently, Jones calculus in the classical formalism. Leaving aside for a moment the pulsed excitation preparing the states at t = 0 and assuming directly as initial condition the fields with amplitudes (or probability amplitudes) αp,q (0) and βp,q (0), the subsequent time evolution simply reads18:
in the quantum formalism or, equivalently, Jones calculus in the classical formalism. Leaving aside for a moment the pulsed excitation preparing the states at t = 0 and assuming directly as initial condition the fields with amplitudes (or probability amplitudes) αp,q (0) and βp,q (0), the subsequent time evolution simply reads18:

Typical Rabi oscillations are shown in Figure 1a. The exciton-field solution reads similarly but it is not explicitly needed since we are concerned in the time dynamics of the optical field only, say in the circular polarization basis, obtained by tracing over the matter  . In the following, we will call
. In the following, we will call  the relative optical phase between the two photon fields at t = 0, and φβ that between the exciton fields. These parameters will play an important role. Another crucial ingredient for the effect to take place is dissipation. For the master equation, this is achieved by turning to the so-called Lindblad form19
the relative optical phase between the two photon fields at t = 0, and φβ that between the exciton fields. These parameters will play an important role. Another crucial ingredient for the effect to take place is dissipation. For the master equation, this is achieved by turning to the so-called Lindblad form19  for the four-fields density matrix, with
for the four-fields density matrix, with  a sum of super-operators
a sum of super-operators  for the generic operator c. Beside the radiative decays of the bare fields (with their corresponding decay rates γa,b) and incoherent pumping Pb from the exciton reservoir, we include as well less common terms that involve directly the dressed states:
for the generic operator c. Beside the radiative decays of the bare fields (with their corresponding decay rates γa,b) and incoherent pumping Pb from the exciton reservoir, we include as well less common terms that involve directly the dressed states:  and
and  . These terms correspond to the dephasing of the upper polariton, that can be either by radiative decay
. These terms correspond to the dephasing of the upper polariton, that can be either by radiative decay  or pure dephasing
or pure dephasing  . We are thus brought to a Liouvillian in the form20
. We are thus brought to a Liouvillian in the form20  . This particular form, with such a choice for the relaxation parameters, is motivated by our experiment and we discuss their physical origin below, but variations—such as decay of the lower polaritons or pumping of another mode—would give the same qualitative phenomenology. For any such dynamics, all the field amplitudes can be solved in closed-form. For the observables of interest, the solution remains fully defined by complex amplitudes:
. This particular form, with such a choice for the relaxation parameters, is motivated by our experiment and we discuss their physical origin below, but variations—such as decay of the lower polaritons or pumping of another mode—would give the same qualitative phenomenology. For any such dynamics, all the field amplitudes can be solved in closed-form. For the observables of interest, the solution remains fully defined by complex amplitudes:

where, for our particular choice of dissipative channels:



Rabi oscillations of polarized beams. (a) Rabi oscillations (theory) (i) in one polarization only (till t ≈ 3 ps), resulting in an oscillating intensity (purple line) of constant polarization (yellow line), and (ii) in two polarizations, reversing the pattern of oscillations. (b) Experimental observation of the effect through the cavity field (along the diameter of the Gaussian spot of 20 μm over a 10 ps duration) with left (red) and right (blue) circular polarization as a false color plot. In the experiment, the leakage of photons results in an exponential decay of the signal. See also Supplementary Movies S1 and S2. (c) Spatial distributions of the density and polarization at 200 fs time intervals during one of the initial cycles after the second pulse arrival. As can be seen while the emitted intensity remains basically constant (height scale in c) the resulting polarization is strongly affected by the Rabi oscillations (mutual oscillations in b and polarization map in c). See also Supplementary Movie S3. The polarization can also be made homogeneous or not spatially.
This simple dynamics can give rise to interesting effects, as discussed below, and implemented in the laboratory thanks to the setup described in next section.
Experimental setup
To implement in the laboratory the effects to be discussed shortly, we used a GaAs polariton microcavity in the regime of Rabi oscillations, with lower and upper polariton branches at 836.2 nm and 833.2 nm, respectively (at T = 13 K). A sketch of our setup is shown in Figure 2, which is based on the principles of the time-resolved digital holography20. Other relevant details are described elsewhere20,21. Two femtosecond pulses with adjustable delay and polarization excite the system. In our setup, the pulses are initially linearly polarized and subsequently passed through quarter wavelength plates to make them counter-circularly polarized. The energy spread of the pulses overlaps with both polariton branches with a relative weight that can be tuned with the pulse mean energy. This triggers Rabi oscillations between excitons and photons.
Setup that implements the effect experimentally. The effect is implemented and observed with a time-resolved digital holography setup for counter-polarized double pulse experiments. The fs pulses train is first split in a reference beam ( ) and an excitation beam (
) and an excitation beam ( ). This latter beam is further divided into twin pulses of equal
). This latter beam is further divided into twin pulses of equal  linear polarizations, of which, only one, upon double passage onto a λ/4 plate, becomes
linear polarizations, of which, only one, upon double passage onto a λ/4 plate, becomes  linear. After rejoining their paths, the twins are made counter-circular (by use of a second λ/4 plate). Their mutual delay (delay 2) can be set on the timescale of the Rabi period (with Φ) or optical period (with φα). The emission from the microcavity sample (MC) is then filtered in polarization and let to interfere with the reference on the detecting CCD camera, before digital elaboration. The evolution of the emission can be tracked by tuning the time of interference by means of the delay stage (delay 1).
linear. After rejoining their paths, the twins are made counter-circular (by use of a second λ/4 plate). Their mutual delay (delay 2) can be set on the timescale of the Rabi period (with Φ) or optical period (with φα). The emission from the microcavity sample (MC) is then filtered in polarization and let to interfere with the reference on the detecting CCD camera, before digital elaboration. The evolution of the emission can be tracked by tuning the time of interference by means of the delay stage (delay 1).
Results and discussion
Dynamics of polarization
The dynamics of Rabi oscillation in the linear regime for each polarization in isolation is simple: we have given it in closed-form in Equations (2) and (3) for both the conservative and dissipative scenarios. Unless otherwise noted, we will assume for the rest of this discussion that the fields are classical, which is the case of our experiment. Although uncoupled, a judicious combination of the two polarizations can however result in nontrivial effects for the combined light. This is illustrated in Figure 1a. After a first pulse exciting both polaritons and thus triggering Rabi oscillations with the same (say circular) polarization, the intermittent transfer of light to the exciton field results in a temporary switch-off of the cavity emission. The system thus emits a field of constant polarization with an oscillating intensity, as shown till t = 3 ps on the figure. Now, if a second pulse of opposite polarization is such that Rabi oscillations are out-of-phase with those triggered by the first pulse, one then gets to the reversed situation of a constant intensity of oscillating polarization, as also seen on the figure.
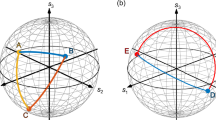
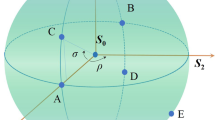
The dynamics of polarization is conveniently pictured on the Poincaré sphere. In the case without decay or with the same decay rate for both types of polaritons (upper and lower), the trajectory is a circle, shown as a green trace in Figure 3. Depending on the respective polariton states for the two polarizations, various circles are realized, from an equator for full-amplitude Rabi oscillations (panel a) down to a single point for polaritons in both polarizations (panel b). The circle thus formed can be defined on the sphere, in a given basis (we will work in the circular one) by two couples of angles  for ξ = α, β, defined by the ratios of polarization
for ξ = α, β, defined by the ratios of polarization  and
and  of the photon α and matter β fields at t = 0, respectively. The relation follows straightforwardly from Equation (2) by geometric construction as:
of the photon α and matter β fields at t = 0, respectively. The relation follows straightforwardly from Equation (2) by geometric construction as:


Dynamics of polarization on the Poincaré sphere (theory). The green arrows, defined by the angles θα and θβ, fix the circle of polarization in absence of decay ( ) by intersecting the meridian of azimuthal angle φα. The red arrow, defined by the angle
) by intersecting the meridian of azimuthal angle φα. The red arrow, defined by the angle  , fixes the point of long-time polarization. In presence of decay,
, fixes the point of long-time polarization. In presence of decay,  , the trajectory of the polarization, in blue, drifts from the green circle to the red final point. (a) Span of the northern hemisphere of the Poincaré sphere in circular polarization, by setting
, the trajectory of the polarization, in blue, drifts from the green circle to the red final point. (a) Span of the northern hemisphere of the Poincaré sphere in circular polarization, by setting  ,
,  , and
, and  with
with  . (b) Span of the full Poincaré sphere from the antidiagonal to the diagonal pole, by setting
. (b) Span of the full Poincaré sphere from the antidiagonal to the diagonal pole, by setting  ,
,  , and
, and  for
for  . (c) Span of the Poincaré sphere excluding a spherical cap of antidiagonal polarization, by setting
. (c) Span of the Poincaré sphere excluding a spherical cap of antidiagonal polarization, by setting  ,
,  , and
, and  . (d) Distorted spanning of the sphere by choosing close initial and final points, by setting
. (d) Distorted spanning of the sphere by choosing close initial and final points, by setting  ,
,  , and Φα = π/2. Parameters common to all cases: blue trajectories with
, and Φα = π/2. Parameters common to all cases: blue trajectories with  and the purple trajectory with
and the purple trajectory with  .
.
This is illustrated in Figure 3c, where the case Φξ = 0, θα = π/4, and θβ = 3π/4 is shown. The field emitted by the cavity as a result goes round the circle in one period of oscillations, that is given by the polariton splitting, and is roughly equal to 1 ps in our case. The particular case already mentioned where the circle vanishes to a single point, defining a polariton—i.e., an eigenstate of the system with no temporal dynamics—corresponds to θα = θβ and Φα = Φβ. The polarization of light is then fixed to that of the corresponding polariton.
Spanning the sphere thanks to polariton features
We can now take advantage of a feature that is usually regarded as a shortcoming of microcavity polaritons, but that in our case will turn the simple effect just proposed into a mechanism that powers a new type of light. It is an experimental fact that there is a significant lifetime imbalance of the two types of polaritons20, with the upper polariton  (that is with βp = αp) being much more short-lived as compared to the lower polariton
(that is with βp = αp) being much more short-lived as compared to the lower polariton  , regardless of the polarizations p. This is commonly attributed to the vicinity of the interband absorption edge and the phonon-assisted relaxation of polaritons from the bottom of the upper branch to high-k states of the lower branch22,23. The exact mechanism is however not important for our purpose. Its theoretical description is easily accounted for phenomenologically by the Lindblad terms expressed with polariton operators. The upper polariton lifetime is typically of the order of 2 ps while the lower polariton lifetime is of the order of 10 ps. These values can furthermore be tuned by orders of magnitude with the already existing technology24. This results in time-dependent Rabi oscillations that converge toward a monotonously decaying signal as the population of the upper polaritons “evaporates” and only lower polaritons remain. The overall dynamics of polarization is therefore that which starts by describing the circle of the Rabi dynamics in absence of dissipation, with a continuous drift toward the fixed point of polarization of the lower polariton. As a consequence of these various effects acting together, one obtains as the light emitted by the device a beam that samples in time a large amount of the possible states of polarization. Various particular cases are shown as blue traces in Figure 3. When starting from a single point, as is the case of panel b, a full mapping of the sphere is realized from one pole to the other. This provides, therefore, a full Poincaré beam in time.
, regardless of the polarizations p. This is commonly attributed to the vicinity of the interband absorption edge and the phonon-assisted relaxation of polaritons from the bottom of the upper branch to high-k states of the lower branch22,23. The exact mechanism is however not important for our purpose. Its theoretical description is easily accounted for phenomenologically by the Lindblad terms expressed with polariton operators. The upper polariton lifetime is typically of the order of 2 ps while the lower polariton lifetime is of the order of 10 ps. These values can furthermore be tuned by orders of magnitude with the already existing technology24. This results in time-dependent Rabi oscillations that converge toward a monotonously decaying signal as the population of the upper polaritons “evaporates” and only lower polaritons remain. The overall dynamics of polarization is therefore that which starts by describing the circle of the Rabi dynamics in absence of dissipation, with a continuous drift toward the fixed point of polarization of the lower polariton. As a consequence of these various effects acting together, one obtains as the light emitted by the device a beam that samples in time a large amount of the possible states of polarization. Various particular cases are shown as blue traces in Figure 3. When starting from a single point, as is the case of panel b, a full mapping of the sphere is realized from one pole to the other. This provides, therefore, a full Poincaré beam in time.
The final state of polarization can be parametrized in the same way as the initial one without decay—with a couple of angles  —by making a rotation of the polariton basis. This introduces the parameters
—by making a rotation of the polariton basis. This introduces the parameters  and
and  from which one obtains the angles
from which one obtains the angles  and
and  (cf. Equation (5)). Any polarization trajectory can thus be fixed by three (possibly complex) numbers: Rα and Rβ for the initial point and
(cf. Equation (5)). Any polarization trajectory can thus be fixed by three (possibly complex) numbers: Rα and Rβ for the initial point and  for the final point. We now come back to the problem of the pulsed excitation of the system into the states
for the final point. We now come back to the problem of the pulsed excitation of the system into the states  , which will give rise to the sought spanning of the polarization sphere. The states themselves are obtained from the R parameters through the relations
, which will give rise to the sought spanning of the polarization sphere. The states themselves are obtained from the R parameters through the relations  ,
,  , and
, and  for an arbitrary (nonzero)
for an arbitrary (nonzero)  . In general, one can prepare any initial state of a two-level system provided that the amplitude of the exciting pulse can be controlled in time25. The situation is even simpler for the preparation of coherent states of two coupled harmonic oscillators (assumed here at resonance for simplicity): a simple Gaussian pulse with Hamiltonian
. In general, one can prepare any initial state of a two-level system provided that the amplitude of the exciting pulse can be controlled in time25. The situation is even simpler for the preparation of coherent states of two coupled harmonic oscillators (assumed here at resonance for simplicity): a simple Gaussian pulse with Hamiltonian  , of width σ in frequency and impinging at time t0 and energy
, of width σ in frequency and impinging at time t0 and energy  as compared to the bare frequency, creates the state
as compared to the bare frequency, creates the state  provided that:
provided that:

In absence of dissipation, the state evolves according to Equation (2). The second pulse must be sent at the frequency specified by Equation (6) to complete the state preparation in the other polarization. Only the relative phase between the two polarized states matters, which is fixed by setting a time delay  between them. This time delay should be small enough so that the first polarization does not depart notably from the circle defined by the first pulse, which is always possible whenever the optical frequency is much higher than the Rabi frequency. The frequency width σ of the pulses can be varied as well: broad (narrow) pulses require excitation
between them. This time delay should be small enough so that the first polarization does not depart notably from the circle defined by the first pulse, which is always possible whenever the optical frequency is much higher than the Rabi frequency. The frequency width σ of the pulses can be varied as well: broad (narrow) pulses require excitation  covering large (small) windows around the polariton resonances to span the entire sphere, with
covering large (small) windows around the polariton resonances to span the entire sphere, with  offering a good compromise. While all trajectories are accessible in a given polarization basis (here circular), if some would turn out to be inconvenient for the available pulse widths (requiring excitations too far from the polaritons), it is then possible to turn to another basis of polarization, e.g.,
offering a good compromise. While all trajectories are accessible in a given polarization basis (here circular), if some would turn out to be inconvenient for the available pulse widths (requiring excitations too far from the polaritons), it is then possible to turn to another basis of polarization, e.g.,  , to achieve the same result with more convenient excitation windows. In this way, since the final point can be independently tuned from the initial points, one can thus span the Poincaré sphere of polarization in essentially any desired way. An applet is available online to control the dynamics of polarization26.
, to achieve the same result with more convenient excitation windows. In this way, since the final point can be independently tuned from the initial points, one can thus span the Poincaré sphere of polarization in essentially any desired way. An applet is available online to control the dynamics of polarization26.
Experimental implementation
By following the above procedure, we are able to realize various cases of interest predicted by the theory. Two limiting situations which have been experimentally implemented are shown in Figure 4, where we present the detected polarization in all the bases, namely (a, f)  , (b, g)
, (b, g)  , and (c, h)
, and (c, h)  . We show in each case the intensity of light emitted in each component,
. We show in each case the intensity of light emitted in each component,  and the corresponding degree of polarization Sp. The initial conditions were selected to evidence two particular effects, namely, of Rabi oscillations in both polarizations either in-phase or anti-phase. This was realized by equal overlap of the polariton branches with both pulses and setting the delay between them to obtain (1) peak-to-peak correspondence (
and the corresponding degree of polarization Sp. The initial conditions were selected to evidence two particular effects, namely, of Rabi oscillations in both polarizations either in-phase or anti-phase. This was realized by equal overlap of the polariton branches with both pulses and setting the delay between them to obtain (1) peak-to-peak correspondence ( , panel c) between the two circular polarizations, and (2) peak-to-node correspondence (
, panel c) between the two circular polarizations, and (2) peak-to-node correspondence ( , panel h), respectively. The resulting combinations are then (1) an oscillating intensity with an essentially fixed polarization (panels d, e) and (2) an oscillating polarization with almost constant intensity (except for the decay, panels i, j). The points are experimental data and the lines are theory fits with the model presented above supplemented with the dynamics of excitation by femtosecond polarized pulses (details of the full model are given in Ref. 20). While all polarizations are measured experimentally, only two polarizations are needed by the theory to obtain the other ones. We have checked the consistency of the model and the observation by fitting polarizations in all bases and by their reconstruction from one basis only. Experimentally, only the photonic field is accessible, but the theory allows to reach the exciton field as well. Therefore, we are able to reconstruct the polarization dynamics, as shown in Figure 4d, 4i, 4e and 4j with a 3D (2D+time) representation of the polarization. Such envelopes of the electric field show vividly how various states of polarization get visited in succession. If a molecule in the path of such a beam would scatter light for a given type of its polarization, the full Poincaré beam would ultimately provide it, thereby offering an optimized exciting light, even for a gas of randomly oriented emitters. This could also be used for temporal tagging, in a similar way that full Poincaré beams have been used spatially for sub-wavelengths localization. The dynamics of polarization is more clearly visualized on the Poincaré sphere. Figure 4 shows how the beam of light emitted by the microcavity provides an ultra-fast sweeping of, in these cases, a hemisphere of the Poincaré sphere, in one case, Figure 4a–4e, with a fast transition toward the final point and in the other, Figure 4f–4j, with a slow whirling round, spanning half the sphere, in agreement with the theoretical model shown in Figure 3d. In all cases, the agreement between theory and experiment is excellent.
, panel h), respectively. The resulting combinations are then (1) an oscillating intensity with an essentially fixed polarization (panels d, e) and (2) an oscillating polarization with almost constant intensity (except for the decay, panels i, j). The points are experimental data and the lines are theory fits with the model presented above supplemented with the dynamics of excitation by femtosecond polarized pulses (details of the full model are given in Ref. 20). While all polarizations are measured experimentally, only two polarizations are needed by the theory to obtain the other ones. We have checked the consistency of the model and the observation by fitting polarizations in all bases and by their reconstruction from one basis only. Experimentally, only the photonic field is accessible, but the theory allows to reach the exciton field as well. Therefore, we are able to reconstruct the polarization dynamics, as shown in Figure 4d, 4i, 4e and 4j with a 3D (2D+time) representation of the polarization. Such envelopes of the electric field show vividly how various states of polarization get visited in succession. If a molecule in the path of such a beam would scatter light for a given type of its polarization, the full Poincaré beam would ultimately provide it, thereby offering an optimized exciting light, even for a gas of randomly oriented emitters. This could also be used for temporal tagging, in a similar way that full Poincaré beams have been used spatially for sub-wavelengths localization. The dynamics of polarization is more clearly visualized on the Poincaré sphere. Figure 4 shows how the beam of light emitted by the microcavity provides an ultra-fast sweeping of, in these cases, a hemisphere of the Poincaré sphere, in one case, Figure 4a–4e, with a fast transition toward the final point and in the other, Figure 4f–4j, with a slow whirling round, spanning half the sphere, in agreement with the theoretical model shown in Figure 3d. In all cases, the agreement between theory and experiment is excellent.
Experimental observation of the effect. Rabi in-phase experiment (a–e), i.e., the Rabi oscillations from the two different pulses start with the same phase, and Rabi antiphase experiment (f–j), i.e., the Rabi oscillations start with an opposite phase. The experimental data (a–c, f–h, black dots) is fitted by the theoretical model (solid lines), providing the amplitudes  and degrees of polarizations Sp. The dynamics of polarization can be displayed on the Poincaré sphere (d, i), demonstrating the rapid transition to the linear polarization in (d) and the spanning of the full hemisphere polarization in (i). (e, j) 2D + t representation of the polarization flow over a 10 ps time span: the surface represents the envelope of the electric field and the color (from red to blue) is scaled on the instantaneous field amplitude. Fitting parameters: g = 4.02 ps−1, γa = 0.2 ps−1, γU = 0.43 ps−1,
and degrees of polarizations Sp. The dynamics of polarization can be displayed on the Poincaré sphere (d, i), demonstrating the rapid transition to the linear polarization in (d) and the spanning of the full hemisphere polarization in (i). (e, j) 2D + t representation of the polarization flow over a 10 ps time span: the surface represents the envelope of the electric field and the color (from red to blue) is scaled on the instantaneous field amplitude. Fitting parameters: g = 4.02 ps−1, γa = 0.2 ps−1, γU = 0.43 ps−1,  , σ = 1/0.15 ps−1. (a–e) Δτ = 1.55 ps, (f–j) Δτ = 1.13 ps.
, σ = 1/0.15 ps−1. (a–e) Δτ = 1.55 ps, (f–j) Δτ = 1.13 ps.
Advantages and extensions
The problem of shaping the polarization of light is one with thriving communities and a vast literature, be it for pulse shaping in time or full Poincaré beams in space. Both fields rely on their own set of techniques, that come with their respective limitations. For instance, since conventional solid state lasers typically emit light with a fixed linear polarization27, and optical nano-antennas also generally radiate a fixed polarization determined by their geometrical structure28,29, the synthesizing of a desired polarization in space30 or time1 is an involved process. Time-varying polarization is particularly demanding as it requires a combination of liquid crystals, spatial light modulators, interferometers, and computer resources with construction algorithms as well as state of the art pulse-shaping techniques, that all together make up a complex setup and impose some restrictions, such as the duration of the pulse31. Beside bringing together both perspectives, our scheme also adds the great freedom of a fundamental and ubiquitous phenomenon, that of Rabi oscillations. This allows to pick from the great repository of platforms featuring such physics the one that will best serve a given purpose, timescale or type of polarized field. We have implemented it in a semiconductor planar microcavity, i.e., in a largely self-contained integrated device of micrometer size which does not rely on extrinsic processing of the signal. As such, this improves on the unwieldy complexity of the setups required to perform polarization shaping. The dynamics in our experiment takes place in a femtosecond timescale, as in many pulse shaping counterparts, but unlike these cases, it has no intrinsic restriction to a particular timescale and turning to other systems with Rabi frequencies of different magnitudes, the same dynamics can be realized with today’s technology in time ranges that run from attoseconds (with plexitons32,33) to milliseconds (with nanomechanical oscillators34). Since Rabi oscillations cannot be distinguished from beatings between two modes35, our effect could also be implemented by two independent filters, provided that one is able to tune independently their lifetimes. However this is not straightforward to realize in practice since the beam should be split to be sent into the filters and subsequently phase-locked onto the target. In this respect, the polariton system offers several advantages: first it provides the phase locking of two independent beams self-consistently. Then, it offers the possibility of tuning the Rabi frequency by external means, such as applying an external electric or magnetic field or changing the exciton–photon detuning. Finally, it provides a convenient way of tuning the lifetime imbalance by dephasing of one of the two polariton branches. Equation (4c) indeed states that it does not matter which mechanism is responsible for the loss of the upper polaritons, only the total decay rate of its coherent fraction enters the dynamics.
In the literature, a variety of multiple polarized beams are implemented by setting space profiles with different polarization. A noticeable example is that of radial (hedgehog) or azimuthal polarization field states realizable, e.g., by use of Q-plate devices36. Here, we have used essentially spatially homogeneous profiles in the experiments, as seen in the time-space chart in Figure 1b and 1c, to focus on the time dynamics instead. Nevertheless, a spatially dependent polarization could also be combined with the temporal dynamics we have highlighted. One of the easiest space patternings would consist of sending the second pulse with a slight angle of incidence (i.e., a Δkα) with respect to the first one. In this case, while co-polarized beams would give interference fringes of amplitude, Rabi-oscillating in time (hence moving with a 2g/Δkα velocity), in the case of counter-polarized beams, all the dynamics discussed in the present work could be obtained with an associated phase delay between the fringes. Each fringe could be made time-oscillating in polarization and with a phase offset with respect to each other, giving rise to a flow of polarization waves with Rabi time period and settable space period, the whole drifting toward the fixed polarization state of the LP polariton. Such effects are beyond the scope of this work but give a hint as to the rich patterns of polarization texture that are within reach, when powered by the dynamics of polariton fluids37.
Conclusions
We have proposed and implemented a new type of pulsed polarized light taking all states of polarization in the time duration of each pulse. The effect relies on the ubiquitous dynamics of Rabi oscillations, in the linear regime, and is therefore versatile as regard to both platforms and timescales. Our experimental implementation in a semiconductor microcavity provides a proof of principle and should allow to disseminate the usage of time-dependent polarization beams as well as allow its extension to the quantum regime by powering the same mechanism with quantum Rabi oscillations.
Competing interests
The authors declare no competing financial interests.
Authors’ contributions
David Colas, Anastasiia A Pervishko, Timothy CH Liew, Ivan A Shelykh, Elena del Valle, and Fabrice P Laussy developed the theory, David Colas fitted the data and analyzed the results, Lorenzo Dominici, Stefano Donati, Dario Ballarini, Milena de Giorgi, and Giuseppe Gigli set up the experiment, Alexey V Kavokin proposed the effect, Fabrice P. Laussy wrote the text, Elena del Valle supervised the theory, Alberto Bramati provided the sample, Lorenzo Dominici supervised the experiment, Daniele Sanvitto supervised and coordinated the research. All the authors discussed the results and contributed to the manuscript.
References
Brixner T, Gerber G . Femtosecond polarization pulse shaping. Opt Lett 2001; 26: 557–559.
Sato M, Higuchi T, Kanda N, Konishi K, Yoshioka K et al. Terahertz polarization pulse shaping with arbitrary field control. Nat Photonics 2013; 7: 724–731.
Brixner T, Krampert G, Pfeifer T, Selle R, Gerber G et al. Quantum control by ultrafast polarization shaping. Phys Rev Lett 2004; 92: 208301.
Aeschlimann M, Bauer M, Bayer D, Brixner T, de Abajo FJG et al. Adaptive subwavelength control of nano-optical fields. Nature 2007; 446: 301–304.
Köhler J, Wollenhaupt M, Bayer T, Sarpe C, Baumert T . Zeptosecond precision pulse shaping. Opt Express 2011; 19: 11638–11653.
Brif C, Chakrabarti R, Rabitz H . Control of quantum phenomena: past, present and future. New J Phys 2010; 12: 075008.
Brown TG, Zhan Q . Focus issue: unconventional polarization states of light. Opt Express 2010; 18: 10775–10776.
Youngworth KS, Brown TG . Focusing of high numerical aperture cylindrical-vector beams. Opt Express 2000; 7: 77–87.
Beckley AM, Brown TG, Alonso MA . Full Poincaré beams. Opt Express 2010; 18: 10777–10785.
Nolte S, Momma C, Kamlage G, Ostendorf A, Fallnich C et al. Polarization effects in ultrashort-pulse laser drilling. Appl Phys A 1999; 68: 563–567.
Meier M, Romano V, Feurer T . Material processing with pulsed radially and azimuthally polarized laser radiation. Appl Phys A 2007; 86: 329–334.
Dausinger F, Lichtner F, Lubatschowski H, editors. Femtosecond Technology for Technical and Medical Applications. London: Springer; 2004.
Rabi II . Space quantization in a gyrating magnetic field. Phys Rev 1937; 51: 652–654.
Khitrova G, Gibbs HM, Kira M, Koch SW, Scherer A . Vacuum Rabi splitting in semiconductors. Nat Phys 2006; 2: 81–90.
Kavokin A, Baumberg JJ, Malpuech G, Laussy FP . Microcavities, 2nd edn. Oxford: Oxford University Press; 2011.
Weisbuch C, Nishioka M, Ishikawa A, Arakawa Y . Observation of the coupled exciton-photon mode splitting in a semiconductor quantum microcavity. Phys Rev Lett 1992; 69: 3314–3317.
Norris TB, Rhee JK, Sung CY, Arakawa Y, Nishioka M et al. Time-resolved vacuum Rabi oscillations in a semiconductor quantum microcavity. Phys Rev B 1994; 50: 14663–14666.
Laussy FP, del Valle E, Tejedor C . Luminescence spectra of quantum dots in microcavities. I. Bosons. Phys Rev B 2009; 79: 235325.
del Valle E . Microcavity Quantum Electrodynamics. Saarbrücken: VDM Verlag; 2010.
Dominici L, Colas D, Donati S, Cuartas JPR, Giorgi MD et al. Ultrafast control and rabi oscillations of polaritons. Phys Rev Lett 2014; 113: 226401.
Ballarini D, Giorgi MD, Cancellieri E, Houdré R, Giacobino E et al. All-optical polariton transistor. Nat Comm 2013; 4: 1778.
Lin SC, Chen JR, Lu TC . Broadening of upper polariton branch in GaAs, GaN, and ZnO semiconductor microcavities. Appl Phys B 2011; 103: 137–144.
Martín M, Ballarini D, Amo A, Viña L, André R . Dynamics of polaritons resonantly created at the upper polariton branch. Superlatt Microstruct 2011; 41: 328–332.
Steger M, Liu G, Nelsen B, Gautham C, Snoke DW et al. Long-range ballistic motion and coherent flow of long-lifetime polaritons. Phys Rev B 2013; 88: 235314.
Golubev NV, Kuleff AI . Control of populations of two-level systems by a single resonant laser pulse. Phys Rev A 2014; 90: 035401.
Colas D, del Valle E, Laussy FP . Polarized polariton fields on the Poincaré sphere. Wolfram Demonstrations Project; 2015. http://demonstrations.wolfram.com/PolarizedPolaritonFieldsOnThePoincareSphere.
Baranov A, Tournie E . Semiconductor Lasers, Fundamentals and Applications. Cambridge: Woodhead Publishing; 2013.
Rodríguez-Fortuño FJ, Marino G, Ginzburg P, O’Connor D, Martínez A et al. Near-field interference for the unidirectional excitation of electromagnetic guided modes. Science 2013; 19: 328–330.
Abasahl B, Dutta-Gupta S, Santschi C, Martin OJF . Coupling strength can control the polarization twist of a plasmonic antenna. Nano Lett 2013; 13: 4575–4579.
Lerman GM, Stern L, Levy U . Generation and tight focusing of hybridly polarized vector beams. Opt Express 2010; 26: 27650–27657.
Polachek L, Oron D, Silberberg Y . Full control of the spectral polarization of ultrashort pulses. Opt Lett 2006; 31: 631–633.
Schlather AE, Large N, Urban AS, Nordlander P, Halas NJ . Near-field mediated plexcitonic coupling and giant Rabi splitting in individual metallic dimers. Nano Lett 2013; 13: 3281–3286.
Vasa P, Wang W, Pomraenke R, Lammers M, Maiuri M et al. Real-time observation of ultrafast Rabi oscillations between excitons and plasmons in metal nanostructures with J-aggregates. Nat Photonics 2013; 7: 128–132.
Faust T, Rieger J, Seitner MJ, Kotthaus JP, Weig EM . Coherent control of a classical nanomechanical two-level system. Nat Phys 2013; 9: 485–488.
Wang C, Vyas R . Fokker-planck equation for a single two-level atom: applications in the bad-cavity limit. Phys Rev A 1995; 51: 2516–2529.
Cardano F, Karimi E, Slussarenko S, Marrucci L, de Lisi C et al. Polarization pattern of vector vortex beams generated by q-plates with different topological charges. App Optics 2012; 51: C1–C6.
Carusotto I, Ciuti C . Quantum fluids of light. Rev Mod Phys 2013; 85: 299–366.
Acknowledgements
We acknowledge funding from the MIUR project Beyond Nano, the ERC Grant POLAFLOW (308136), the IEF project SQUIRREL (623708) and the support from IRSES project POLAPHEN.
Note: Accepted article preview online 29 June 2015
Author information
Authors and Affiliations
Corresponding author
Additional information
Note: Supplementary information for this article can be found on the Light: Science & Applications' website.
Rights and permissions
This license allows readers to copy, distribute and transmit the Contribution as long as it attributed back to the author. Readers are permitted to alter, transform or build upon the Contribution as long as the resulting work is then distributed under this is a similar license. Readers are not permitted to use the Contribution for commercial purposes. Please read the full license for further details at - http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Colas, D., Dominici, L., Donati, S. et al. Polarization shaping of Poincaré beams by polariton oscillations. Light Sci Appl 4, e350 (2015). https://doi.org/10.1038/lsa.2015.123
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2015.123
Keywords
This article is cited by
-
Coupled quantum vortex kinematics and Berry curvature in real space
Communications Physics (2023)
-
Disaster management using free space optical communication system
Photonic Network Communications (2020)
-
Optically reconfigurable polarized emission in Germanium
Scientific Reports (2018)
-
Superluminal X-waves in a polariton quantum fluid
Light: Science & Applications (2017)
-
Spin-dependent manipulating of vector beams by tailoring polarization
Scientific Reports (2016)