Abstract
We demonstrate that the combination of digital spiral imaging with high-dimensional orbital angular momentum (OAM) entanglement can be used for efficiently probing and identifying pure phase objects, where the probing light does not necessarily touch the object, via the experimental, non-local decomposition of non-integer pure phase vortices in OAM-entangled photon pairs. The entangled photons are generated by parametric downconversion and then measured with spatial light modulators and single-mode fibers. The fractional phase vortices are defined in the idler photons, while their corresponding spiral spectra are obtained non-locally by scanning the measured OAM states in the signal photons. We conceptually illustrate our results with the biphoton Klyshko picture and the effective dimensionality to demonstrate the high-dimensional nature of the associated quantum OAM channels. Our result is a proof of concept that quantum imaging techniques exploiting high-dimensional entanglement can potentially be used for remote sensing.
Similar content being viewed by others
Introduction
In 1992, Allen and co-workers recognized that a light beam with a helical phasefront of exp(iℓϕ) carries a well-defined orbital angular momentum (OAM) of ℓℏ per photon, where ℓ is an integer and ϕ is the azimuthal angle1. In 2002, Leach and co-workers2 developed an interferometric technique to distinguish and route single photons according to their individual OAM states. The associated OAM eigenstates,  , form a complete, orthogonal and infinite-dimensional basis3 and have been demonstrated to be a useful degree of freedom exploited for quantum information applications in a high-dimensional Hilbert space.4,5 The discrete OAM spectrum (or spiral spectrum) can also be useful for imaging, such as in the work of Torner et al.6 called digital spiral imaging. In their work, a fundamental Gaussian beam illuminates a sample to be probed. Then the sample scatters the beam and alters its OAM components. By analyzing the spiral spectrum of the scattered beam, one can thus extract a wealth of information from the object. This technique can be effectively used to probe canonical geometrical objects.7 Recently, this technique has also been extended to study and characterize the position of the dielectric sphere on the micrometer scale.8
, form a complete, orthogonal and infinite-dimensional basis3 and have been demonstrated to be a useful degree of freedom exploited for quantum information applications in a high-dimensional Hilbert space.4,5 The discrete OAM spectrum (or spiral spectrum) can also be useful for imaging, such as in the work of Torner et al.6 called digital spiral imaging. In their work, a fundamental Gaussian beam illuminates a sample to be probed. Then the sample scatters the beam and alters its OAM components. By analyzing the spiral spectrum of the scattered beam, one can thus extract a wealth of information from the object. This technique can be effectively used to probe canonical geometrical objects.7 Recently, this technique has also been extended to study and characterize the position of the dielectric sphere on the micrometer scale.8
Here, we measure the digital spiral spectrum in a ghost-imaging set-up using a fractional helical phase as an object. Ghost imaging is a different approach toward imaging, in which the image can be reconstructed using information from one light beam that never touches the object placed in the other beam.9 This approach was initially developed to reveal the intriguing quantum effects between photon pairs created by spontaneous parametric downconversion (SPDC).10 Recently, ghost imaging explored with OAM quantum correlations has been implemented to achieve the edge contrast enhancement of images.11 Angular ghost diffraction, as an angular analog to conventional diffraction,12 has also been reported, establishing the Fourier relationship between the angle position and OAM for entangled photon pairs.13 Previously, we quantified the high-dimensional quantum nature of angular ghost diffraction using a non-local Young’s double slit.14
In this work, we present a quantum analog to digital spiral imaging, in which we have treated a fractional phase vortex as our object. We report the first experimental non-local spiral spectrum of non-integer phase vortices in OAM-entangled SPDC photon pairs. The non-integer phase vortex is measured in the idler arm (corresponding to the object), while we acquire the corresponding spiral spectra non-locally by scanning the OAM measurements in the signal arm. The use of OAM for probing such pure phase objects is a natural choice because of the characteristic helical phase of OAM. Moreover, because OAM modes are orthogonal, our technique can be used for efficiently probing and identifying pure phase objects in remote sensing. We draw a conceptual OAM Klyshko picture and calculate the effective dimensionality of the channels probed by the fractional phase vortices with respect to the actual measured spiral bandwidth.
Materials and methods
Theoretical method
We focus on fractional phase vortices, which we treat as the object to be probed. Mathematically, the phase of vortex beams is characterized by exp (iMϕ), where M is the topological charge, which is not restricted to an integer.15 Such beams are called non-integer phase vortices rather than non-integer OAM16 because M is generally not equal to the OAM expectation per photon.17 Various methods have been proposed to generate such a fractional vortex, such as the spiral phase plate with fractional step height,18 specially designed holograms,19 a pair of electro-optic phase plates20 and internal conical diffraction.21 These methods can also be used to explore high-dimensional entanglement in downconverted photon pairs. Based on half-integer spiral phase plates, Oemrawsingh et al.22,23 proposed, and later demonstrated experimentally, the high-dimensional quantum entangled nature of a half-integer vortex, although they did not obtain the spiral spectrum experimentally. It has also been demonstrated that the fractional vortices can be introduced in hyperentanglement to increase the related Shannon dimensionality.24 At the single photon level, Gotte et al.25 has generalized the quantum theory of rotation angles to fractional vortices and has demonstrated the theoretical decomposition of fractional vortices into the integer OAM basis of single photons. In this perspective, a fractional vortex represents a multidimensional vector state in a high-dimensional Hilbert space that is spanned by the OAM eigenstates. Here, we establish experimentally the OAM decompositions of such fractional vortices between entangled photon pairs and present a conceptual Klyshko picture that highlights the high-dimensional OAM channels in the entangled photons.
Like linear position and linear momentum, angular position and OAM also form a pair of conjugate variables and can be linked by the discrete Fourier relationship:26


where u(ρ,ϕ,z) describes an arbitrary field distribution, and An(ρ,z) is the corresponding OAM spectrum or spiral spectrum. In analogy with Equations (1) and (2), the angular momentum content of a non-integer phase vortex state,  (α specifies the orientation of edge dislocation), can be calculated from a projection into the basis of integer OAM eigenstates
(α specifies the orientation of edge dislocation), can be calculated from a projection into the basis of integer OAM eigenstates  ,25
,25

where An=eiπ(M−n)sinc[π(M−n)] (sinc(x)=sinx/x). One can see that the orientation of the edge dislocation α brings a phase shift of exp (inα) to each OAM eigenmode.
In SPDC, a pump photon of fundamental Gaussian mode yields a pair of signal and idler photons. The photon pairs are entangled in OAM, and the two-photon state can be written as27

where  is the probability of finding a signal photon (s) with an OAM of ℓℏ and an idler photon (i) with an OAM of −ℓℏ. In our experiment, the idler photon is imparted with the phase of the object, which in this case is a non-integer phase vortex profile, while integer values of OAM are measured in the signal photons. Consequently, given the decomposition of the non-integer phase vortex in Equation (3), the two-photon entangled state of Equation (4) is modified to
is the probability of finding a signal photon (s) with an OAM of ℓℏ and an idler photon (i) with an OAM of −ℓℏ. In our experiment, the idler photon is imparted with the phase of the object, which in this case is a non-integer phase vortex profile, while integer values of OAM are measured in the signal photons. Consequently, given the decomposition of the non-integer phase vortex in Equation (3), the two-photon entangled state of Equation (4) is modified to

By substituting k=−ℓ + n, we can rewrite Equation (5) as

where  . A comparison between Equations (4) and (6) shows that the entangled spiral spectrum is spread by the presence of the non-integer phase mask
. A comparison between Equations (4) and (6) shows that the entangled spiral spectrum is spread by the presence of the non-integer phase mask  in the idler arm. We visualize this spreading effect in Figure 1a and 1b, without loss of generality, where we have assumed Cℓ,−ℓ is constant (maximally entangled) and M=−2/3. If we subsequently project the idler photon into the zero OAM state
in the idler arm. We visualize this spreading effect in Figure 1a and 1b, without loss of generality, where we have assumed Cℓ,−ℓ is constant (maximally entangled) and M=−2/3. If we subsequently project the idler photon into the zero OAM state  , we can then recover the spiral imaging of the phase vortex with M=−2/3 in the signal arm, as shown in Figure 1c. Formally, this post-selection in the idler arm causes the signal photons to collapse into
, we can then recover the spiral imaging of the phase vortex with M=−2/3 in the signal arm, as shown in Figure 1c. Formally, this post-selection in the idler arm causes the signal photons to collapse into

For the maximal entanglement with Cℓ,−ℓ being constant, Equation (7) predicts that the recovery of the spiral spectrum of the non-integer phase vortex is perfect, while in an actual experiment the fidelity is less than unity. Namely,  due to the limited spiral spectrum of the source, characterized by Cℓ,−ℓ;28,29 photon pairs with smaller-valued OAM are produced more frequently than those with higher-valued OAM,
due to the limited spiral spectrum of the source, characterized by Cℓ,−ℓ;28,29 photon pairs with smaller-valued OAM are produced more frequently than those with higher-valued OAM,  if m>n.
if m>n.
Experimental scheme
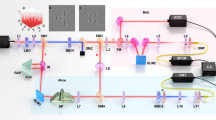
We employ the experimental set-up shown in Figure 2 to demonstrate the non-local decomposition of non-integer phase vortices. A collimated 355-nm beam pumps a 5-mm long β-barium borate (BBO) crystal, where a degenerate 710 nm signal and idler photons are produced in pairs via type-I collinear SPDC and are separated by a non-polarizing beam splitter. The crystal is imaged onto spatial light modulators (SLMs) using a pair of lenses. The definition of non-integer phase vortices and the scanning of OAM measurements are performed separately on these SLMs in the idler and signal arms, respectively. Each SLM is imaged onto a single-mode fiber (SMF) that is connected to an avalanche photodiode serving as single-photon detectors. The outputs of the detectors are fed to a coincidence counting circuit. A longpass filter (IF1) is used to block the pump beam after the crystal, while two bandpass filters (IF2) of width 10 nm and centered at 710 nm are used to ensure that we measure signal and idler photons near degeneracy in front of the SMF.
The non-integer phase vortices are defined in the idler arms, while the corresponding OAM spectra are scanned in the signal arm. The SLMs in individual arms act as computer reconfigurable refractive elements that can imprint any desired phase structure on incoming photons. In practice, the desired phase structure is usually added to a linear grating with a carrier frequency such that the first-order diffracted beam acquires the required phase structure.17 For vortex beams, the design of the diffractive component is the modulo 2π addition of a simple blazed grating with an azimuthal 2πℓϕ phase ramp, yielding the characteristic ℓ-pronged fork dislocation on the beam axis. This design is readily adapted to non-integer M, giving an additional radial discontinuity to the pattern,30 and the orientation of this radial discontinuity coincides with the edge discontinuity of the resultant non-integer vortex. However, as can be seen in Equation (7), the non-local spiral spectrum measured experimentally is the mode weight, namely,  , which is independent of the rotation of edge discontinuity. We show in the upper and bottom insets of Figure 2 the formation of the desired patterns for producing a non-integer vortex of M=−2/3 and an integer OAM state of ℓ=2, respectively.
, which is independent of the rotation of edge discontinuity. We show in the upper and bottom insets of Figure 2 the formation of the desired patterns for producing a non-integer vortex of M=−2/3 and an integer OAM state of ℓ=2, respectively.
Results and discussion
Experimental results
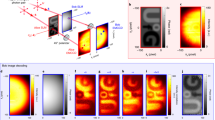
Without loss of generality, we investigate the non-local spiral spectra of four non-integer phase vortices with different topological charges, that is, M=−1/2, −2/3, −5/2 and −8/3. The gratings for producing these phase vortices and the phase profiles of these vortices are shown in the insets of Figure 3. There is a horizontal discontinuity in each grating in addition to the fork dislocation in the center. After scanning OAM from ℓ=−7 to +7 in the signal arm, we obtain the experimental results shown in Figure 3.
The experimental results of quantum digital spiral imaging for different phase vortices: (a) M=−1/2; (b) M=−2/3; (c) M=−5/2; (d) M=−8/3. The red bars are the exact spectra based on Equation (3) (or assuming a maximally entangled two-photon OAM state), while the green ones are the experimental measurements of non-local vortices. The upper and bottom insets in each plot illustrate the desired hologram and vortex phase profile, respectively. OAM, orbital angular momentum.
In each subplot, the red bars are the theoretical predictions of the spiral spectrum for an individual phase vortex based on Equation (3), while the green bars are the experimentally measured spiral spectra. We demonstrate good agreement between the experimental and theoretical spectral profiles, consisting of the probabilities of each ℓ mode. If we denote M=m+μ, where m is the integer part and  is the fractional part, then we find that the distribution is just peaked around m, while the spread profile of the spectra is determined by μ. For a half-integer with μ=1/2 in Figure 3a and 3c, the theory predicts two peaks of equal height at two neighboring integers. However, we observe a slight asymmetry of these two peaks in the ghost experimental set-up. This asymmetry can be attributed to the limited spiral bandwidth, namely,
is the fractional part, then we find that the distribution is just peaked around m, while the spread profile of the spectra is determined by μ. For a half-integer with μ=1/2 in Figure 3a and 3c, the theory predicts two peaks of equal height at two neighboring integers. However, we observe a slight asymmetry of these two peaks in the ghost experimental set-up. This asymmetry can be attributed to the limited spiral bandwidth, namely,  if m>n, as shown in the inset of Figure 4a. In Equation (7), Aℓ is multiplied by coefficients Cℓ,−ℓ, which are ideally constant but actually decrease as the ℓ value increases.
if m>n, as shown in the inset of Figure 4a. In Equation (7), Aℓ is multiplied by coefficients Cℓ,−ℓ, which are ideally constant but actually decrease as the ℓ value increases.
Illustration of OAM quantum channels in the Klyshko picture. (a) Schematic of an entanglement set-up, where the inset shows the present limited spiral spectrum. (b) Backprojection schematic (the dashed lines highlight the channels associated with OAM modes of  ). BBO, β-barium borate; OAM, orbital angular momentum; SMF, single-mode fiber.
). BBO, β-barium borate; OAM, orbital angular momentum; SMF, single-mode fiber.
The OAM eigenstates form an infinite-dimensional, complete set of orthogonal modes and can be used for the classical digital spiral imaging technique using a single-light beam to acquire information of a target object.6,7,8 Our results further suggest that the combination of the spiral imaging technique with an entangled source enables a quantum analog of digital spiral imaging, which can be useful in remote sensing. A one-to-one relationship exists between the non-local spiral spectrum and the spatial shape of the target. Hence, one light beam can illuminate a target phase object, and information on this target can be remotely acquired by analyzing the coincidences as the OAM measurements in the other light beam are scanned through different OAM values.
Klyshko picture and effective dimensionality
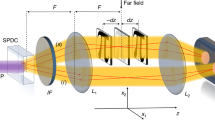
Our results present the quantum analog of digital spiral imaging for entangled photon pairs. We can illustrate this technique via the associated quantum channels by drawing the biphoton OAM Klyshko picture presented in Figure 4. In a conventional Klyshko picture, the signal and idler apparatus are unfolded with respect to the crystal, and the straight lines represent the advanced light rays.31 In contrast, the solid (red) lines in the biphoton OAM Klyshko picture of Figure 4 represent the OAM channels rather than the real light rays.32 As defined previously,33 a channel is an electromagnetic wave whose distinct character allows it to remain independent from others during simultaneous transmission. We can adopt the concept of an OAM channel due to the orthogonality of twisted light beams with different helical indexes.34 As illustrated in Figure 4a, the ultraviolet pump of the BBO crystal coherently emits pairs of Schmidt modes,  , and each can be treated as a biphoton OAM channel. In this scenario, a high-dimensional OAM-entangled state
, and each can be treated as a biphoton OAM channel. In this scenario, a high-dimensional OAM-entangled state  can be regarded as a coherent superposition of these biphoton OAM channels of different indexes ℓ, each with an assigned weight of Cℓ,−ℓ. We show in Figure 4a the case of ℓ=0,±1 (other higher OAM are not shown). The diffractive components displayed in the SLMs, which specify the state being measured, can be regarded as devices that can probe a certain number of the generated OAM channels (referred to as the effective dimensionality; e.g., if the component imparts a helical phase corresponding to a certain integer OAM value, then the effective dimensionality is one35). The SMFs on both arms can support only the fundamental mode; hence, the signal at the detector is a measure of the overlap between the fundamental mode and the resulting field after the generated photons are probed by the phase profiles encoded on the SLMs.
can be regarded as a coherent superposition of these biphoton OAM channels of different indexes ℓ, each with an assigned weight of Cℓ,−ℓ. We show in Figure 4a the case of ℓ=0,±1 (other higher OAM are not shown). The diffractive components displayed in the SLMs, which specify the state being measured, can be regarded as devices that can probe a certain number of the generated OAM channels (referred to as the effective dimensionality; e.g., if the component imparts a helical phase corresponding to a certain integer OAM value, then the effective dimensionality is one35). The SMFs on both arms can support only the fundamental mode; hence, the signal at the detector is a measure of the overlap between the fundamental mode and the resulting field after the generated photons are probed by the phase profiles encoded on the SLMs.
The concept of biphoton OAM channels can also be well understood in light of Klyshko’s advanced wave model,31 as illustrated in Figure 4b. The detector D2 is substituted by a standard light source, and the connected SMF transmits a Gaussian light with zero OAM, namely,  . This light goes backward in time to illuminate SLM1, where the reflected light acquires a desired fractional vortex. Accordingly, the OAM spectrum is spread, namely,
. This light goes backward in time to illuminate SLM1, where the reflected light acquires a desired fractional vortex. Accordingly, the OAM spectrum is spread, namely,  , where the additional reflection occurring on SLM1 has flipped each ℓ to −ℓ. The BBO crystal is replaced by a standard mirror, such that each OAM is flipped again, and
, where the additional reflection occurring on SLM1 has flipped each ℓ to −ℓ. The BBO crystal is replaced by a standard mirror, such that each OAM is flipped again, and  becomes
becomes  , which is identical to
, which is identical to  of Equation (7). We note that Figure 4b does not account for the effect of phase matching, which leads to a limited spiral bandwidth generated by the BBO crystal.36 Because a standard mirror replaces the BBO crystal, all the channels are reflected with equal probability (i.e., the coefficients Cℓ,−ℓ are all unity). If we assume that the mirror in Figure 4b has a mode-dependent reflectivity of Cℓ,−ℓ, then these two models should be equivalent. Thus, as we perform OAM scanning in Figure 4a using a combination of SLM1, SMF and D1 in the signal arm, we obtain the spiral spectra of the fractional vortex, as shown in Figure 3.
of Equation (7). We note that Figure 4b does not account for the effect of phase matching, which leads to a limited spiral bandwidth generated by the BBO crystal.36 Because a standard mirror replaces the BBO crystal, all the channels are reflected with equal probability (i.e., the coefficients Cℓ,−ℓ are all unity). If we assume that the mirror in Figure 4b has a mode-dependent reflectivity of Cℓ,−ℓ, then these two models should be equivalent. Thus, as we perform OAM scanning in Figure 4a using a combination of SLM1, SMF and D1 in the signal arm, we obtain the spiral spectra of the fractional vortex, as shown in Figure 3.
As illustrated in Figure 4a, each OAM channel of  has been assigned an effective weight of AℓCℓ,−ℓ. In other words, the two-photon state post-selected by the idler fractional and signal integer holograms effectively becomes
has been assigned an effective weight of AℓCℓ,−ℓ. In other words, the two-photon state post-selected by the idler fractional and signal integer holograms effectively becomes

Thus, the effective dimensionality (D) of these quantum channels can be given by35,37

Note that in this expression, we have not only considered the decomposition of the fractional vortex (Aℓ) but also the effect of the generated spiral spectrum (Cℓ,−ℓ). From our experiment, we can estimate D if we assume that the higher OAM states do not contribute significantly (the coefficients decrease rapidly with higher OAM values). We compare the experimental effective dimensionalities of the fractional vortex (calculated straightforwardly from Figure 3) to the expected dimensionality (from Equation (9)). The values are listed in Table 1. Compared with a simple integer helical phase, which effectively probes just a single channel, the effective dimensionalities we obtain are all greater than 1.
From a mathematical perspective, M=−1/2 and M=−5/2 (similarly for M=−2/3 and M=−8/3) have the same fractional part μ=1/2 and are thus expected to have the same value D; we attribute the difference to our detection system (including imperfections such as misalignment). Aside from the finite spiral bandwidth of the source, the detection system also has a characteristic bandwidth determined by the geometry of the experiment, such as the sizes of the apertures and details of the imaging, because the spatial modes are also inherently sensitive to the radial field distribution.29,38 The radial distribution is unavoidably truncated in any given experiment, leading to a loss in bandwidth.39 To isolate the effects of detection, one can implement a backprojection experiment,40 where one actually replaces one detector with a laser and ensures that optimal coupling to the other SMF is present. However, for this work, we have used the Klyshko picture mainly as a conceptual tool to understand the high-dimensional OAM channels in the context of quantum digital spiral imaging.
Conclusions
We have presented a quantum analog to classical digital spiral imaging. We demonstrate experimentally the non-local recovery of the spiral spectrum of a phase object using OAM-entangled photons. Although we focused on non-integer phase vortices, our technique, which exploits high-dimensional OAM entanglement, can be applied to probe and characterize pure phase objects as used in remote sensing. The experimental results are in good agreement with the theoretical predictions. The OAM decomposition in terms of the biphoton OAM quantum channels in the ghost set-up can be understood in light of the Klyshko picture. As expected, the effective dimensionality when measuring fractional phase vortices is higher compared with when only integer-valued OAM modes are measured. This finding holds promise for high-dimensional quantum imaging, particularly when using the multidimensional non-integer vortex states.
References
Allen L, Beijersbergen MW, Spreeuw RJ, Woerdman JP . Orbital angular momentum of light and the transformation of Laguerre–Gaussian laser modes. Phys Rev A 1992; 45: 8185–8189.
Leach J, Padgett MJ, Barnett SM, Franke-Arnold S, Courtial J . Measuring the orbital angular momentum of a single photon. Phys Rev Lett 2002; 88: 257901.
Molina-Terriza G, Torres JP, Torner L . Management of the angular momentum of light: preparation of photons in multidimensional vector states of angular momentum. Phys Rev Lett 2001; 88: 013601.
Molina-Terriza G, Torres JP, Torner L . Twisted photons. Nat Phys 2007; 3: 305–310.
Franke-Arnold S, Allen L, Padgett M . Advances in optical angular momentum. Laser Photon Rev 2008; 2: 299–313.
Torner L, Torres JP, Carrasco S . Digital spiral imaging. Opt Express 2005; 13: 873–881.
Molina-Terriza G, Rebane L, Torres JP, Torner L, Carrasco S . Probing canonical geometrical objects by digital spiral imaging. J Eur Opt Soc 2007; 2: 07014.
Petrov D, Rahuel N, Molina-Terriza G, Torner L . Characterization of dielectric spheres by spiral imaging. Opt Lett 2012; 37: 869–871.
Pittman TB, Shih YH, Strekalov DV, Sergienko AV . Optical imaging by means of two-photon quantum entanglement. Phys Rev A 1995; 52: R3429–R3432.
Erkmen BI, Shapiro JH . Ghost imaging: from quantum to classical to computational. Adv Opt Photon 2010; 2: 405–450.
Jack B, Leach L, Romero J, Franke-Arnold S, Ritsch-Marte M et al. Holographic ghost imaging and the violation of a Bell inequality. Phys Rev Lett 2009; 103: 083602.
Jha AK, Jack B, Yao E, Leach J, Boyd RW et al. Fourier relationship between the angle and angular momentum of entangled photons. Phys Rev A 2008; 78: 043810.
Jack B, Padgett MJ, Franke-Arnold S . Angular diffraction. New J Phys 2008; 10: 103013.
Chen LX, Leach J, Jack B, Padgett MJ, Franke-Arnold S et al. High-dimensional quantum nature of ghost angular Young’s diffraction. Phys Rev A 2010; 82: 033822.
Dennis MR, O’Holleran K, Padgett MJ . Singular optics: optical vortices and polarization singularities. Prog Opt 2009; 53: 293–363.
Oemrawsingh SS . Optical dislocations and quantum entanglement. PhD thesis, Leiden University, Leiden, The Netherlands, 2004.
Leach J, Yao E, Padgett MJ . Observation of the vortex structure of a non-integer vortex beam. New J Phys 2004; 6: 71.
Oemrawsingh SS, van Houwelingen JA, Eliel ER, Woerdman JP, Verstegen EJ et al. Production and characterization of spiral phase plates for optical wavelengths. Appl Opt 2004; 43: 688–694.
Tao SH, Lee WM, Yuan X . Experimental study of holographic generation of fractional Bessel beams. Appl Opt 2004; 43: 122–126.
Chen L, She W . Electrically tunable and spin-dependent integer or noninteger orbital angular momentum generator. Opt Lett 2009; 34: 178–180.
O’Dwyer DP, Phelan CF, Rakovich YP, Eastham PR, Lunney JG et al. Generation of continuously tunable fractional optical orbital angular momentum using internal conical diffraction. Opt Express 2010; 18: 16480–16485.
Oemrawsingh SS, Aiello A, Eliel ER, Nienhuis G, Woerdman JP . How to observe high-dimensional two-photon entanglement with only two detectors. Phys Rev Lett 2004; 92: 217901.
Oemrawsingh SS, Ma X, Voigt D, Aiello A, Eliel ER et al. Experimental demonstration of fractional orbital angular momentum entanglement of two photons. Phys Rev Lett 2005; 95: 240501.
Chen LX, She W . Increasing Shannon dimensionality by hyperentanglement of spin and fractional orbital angular momentum. Opt Lett 2009; 34: 1855–1857.
Götte JB, Franke-Arnold S, Zambrini R, Barnetty SM . Quantum formulation of fractional orbital angular momentum. J Mod Opt 2007; 54: 1723–1738.
Yao E, Franke-Arnold S, Courtial J, Barnett S, Padgett M . Fourier relationship between angular position and optical orbital angular momentum. Opt Express 2006; 14: 9071–9076.
Mair A, Vaziri A, Weihs G, Zeilinger A . Entanglement of the orbital angular momentum states of photons. Nature 2001; 412: 313–316.
Torres JP, Alexandrescu A, Torner L . Quantum spiral bandwidth of entangled two-photon states. Phys Rev A 2003; 68: 050301(R).
Di Lorenzo Pires H, Florijn HC, van Exter MP . Measurement of the spiral spectrum of entangled two-photon states. Phys Rev Lett 2010; 104: 020505.
Götte JB, O’Holleran K, Preece D, Flossmann F, Franke-Arnold S et al. Light beams with fractional orbital angular momentum and their vortex structure. Opt Express 2008; 16: 993–1006.
Angelo MD, Shih YH . Quantum imaging. Laser Phys Lett 2005; 2: 567–596.
Chen LX, Wu QP . High-dimensional entanglement concentration of twisted photon pairs. Laser Phys Lett 2012; 9: 759–764.
Torres JP . Optical communications: multiplexing twisted light. Nat Photon 2012; 6: 420–422.
Tamburini F, Mari E, Sponselli A, Thidé B, Bianchini A et al. Encoding many channels on the same frequency through radio vorticity: first experimental test. New J Phys 2012; 14: 033001.
Pors JB, Aiello A, Oemrawsingh SS, van Exter MP, Eliel ER et al. Angular phase-plate analyzers for measuring the dimensionality of multimode fields. Phys Rev A 2008; 77: 033845.
Romero J, Giovannini D, Franke-Arnold S, Barnett SM, Padgett MJ . Increasing the dimension in high-dimensional two-photon orbital angular momentum entanglement. Phys Rev A 2012; 86: 012334.
Law CK, Eberly JH . Analysis and interpretation of high transverse entanglement in optical parametric down conversion. Phys Rev Lett 2004; 92: 127903.
van Exter MP, Aiello A, Oemrawsingh SS, Nienhuis G, Woerdman JP . Effect of spatial filtering on the Schmidt decomposition of entangled photons. Phys Rev A 2006; 74: 012309.
Salakhutdinov VD, Eliel ER, Löffler W . Full-field quantum correlations of spatially entangled photons. Phys Rev Lett 2012; 108: 173604.
McLaren M, Romero J, Padgett MJ, Roux FS, Forbes A . Two-photon optics of Bessel–Gaussian modes. Phys Rev A 2013; 88: 033818.
Acknowledgements
LC thanks Jonathan Leach for previous illuminating discussions about the OAM spreading effect and the National Natural Science Foundation of China (Grant No. 11104233), the Fundamental Research Funds for the Central Universities (Grants Nos. 2011121043, 2012121015), the Natural Science Foundation of Fujian Province of China (2011J05010) and the Program for New Century Excellent Talents in University of China (Grant No. NCET-13-0495). JR thanks Hamamatsu and Miles Padgett for their kind support of this work.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
This work is licensed under the Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Chen, L., Lei, J. & Romero, J. Quantum digital spiral imaging. Light Sci Appl 3, e153 (2014). https://doi.org/10.1038/lsa.2014.34
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2014.34