Abstract
A moiré is an interference pattern that appears when two different periodic structures are overlaid. The image created is extremely sensitive to small variations in the original layers and is thus very interesting for anti-counterfeit protection. We present a microfabricated 1D moiré enabling complex high-resolution patterns as a significantly improved security feature that cannot be reproduced using standard printing methods. Furthermore, we demonstrate, theoretically and experimentally, that a microscopic deviation from the original design results in a macroscopic variation in the moiré that is clearly visible to the naked eye. The record resolution achieved in the elements fabricated and the increased design freedom, make these high-resolution moirés excellent candidates for a variety of visually appealing security applications.
Similar content being viewed by others
Introduction
According to a recent Organisation for Economic Co-operation and Development (OECD, http://www.oecd.org) study, the spread of counterfeit goods has become global in recent years and the range of goods subject to infringement has increased significantly. To help distinguish the originals from the counterfeits, the copyright holder often employs the use of serial numbers and/or holograms. However, the value of holograms as security features has decreased due to two facts: (i) commercial companies exist which can easily reproduce existing holographic images and (ii) they can be replaced by other color patterns and still be perceived as genuine by most observers. For these reasons new optical security features easily recognizable by the naked eye are of great interest. The moiré effect is a well-known optical phenomenon that occurs as a result of interference between superimposed structures, such as line gratings or dot screens. The moiré itself is the new, clearly visible pattern observable when the individual structures are superimposed, although it does not appear in any of the original structures themselves.1 One of the best known examples of this effect is the superposition of repetitive structures formed of alternating black and white lines (line gratings), which yields alternating dark and bright moiré lines known as moiré fringes.2,3 Such moiré fringes have been applied for the analysis of deformation of materials,4,5 as well as for three-dimensional (3D) topography metrology.6
Additionally, it has been shown that a 2D repetitive pattern array, sampled with a 2D array of microlenses, generates a moiré image comprising the enlarged and rotated array of repetitive patterns.7,8,9,10 This kind of moiré is known as a 2D moiré and can be used to create novel security features called ‘moiré magnifiers’. These can be seen in the security thread of several current banknotes,11 such as the 1000 Swedish krona, the 100 Mexican pesos, and the 50 and 100 Danish kroner. However, the size of 2D moiré design elements is severely limited since they must reside within a single period of the 2D pattern array. In order to produce larger sized elements, it would be necessary to increase the pattern array period, but this would drastically reduces the possibility of developing sophisticated design elements at high frequencies.
The 1D moiré12 is a novel alternative that overcomes the design limitations of 2D moirés. The 1D moiré configuration allows for design elements (text, graphics, grayscale, or color motifs) to be freely laid out along the length of the base band. The longer the base band, the more elements can be incorporated without modifying the moiré period. Hence, the 1D moiré enables the creation of features made up of many symbols or letters that can move along rectilinear trajectories when one of the layers is displaced relative to the other.13 A 1D linear moiré consists of a base layer of design features distributed along base bands, and a revealing layer placed over it to sample these graphical features. Usually the base layer is created using printing techniques, and the revealing layer is made by printing a line grating on a transparent film or by using an array of cylindrical microlenses. Such printing techniques provide a minimal line width ranging between 10 and 20 µm. This yields an effective offset printed resolution between 1270 and 2540 dpi. However, this is not sufficient to prevent counterfeiting using desktop scanners and printers.
In this paper, we describe the calculation, design, fabrication and characterization of visually attractive 1D moirés with resolutions up to 9754 dpi. Our new mathematical model determines the geometrical transformations necessary to design esthetic 1D moirés with a circular layout. The moiré elements move along radial or spiral trajectories when the base and the revealing layer are displaced relative to each other. In order to achieve the high resolutions proposed using reliable, cost-efficient and reproducible means, both the base and the revealing layers were manufactured using scalable microfabrication techniques.
Materials and methods
Linear moiré design
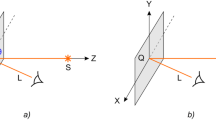
Although the basic theory of the 1D moiré approach is known,13 the mathematical concepts relevant to understanding the design of the proposed high-resolution curvilinear moirés are summarized in Supplementary Information 1. Linear 1D moirés are formed by the superposition of a rectilinear base layer and a rectilinear revealing layer, as represented in Figure 1a. For each desired moiré shape, it is possible to use differently laid out but matching pairs of base and revealing layers, which prevents the direct reproduction of the moiré. Figure 1b shows an example of the relationship between the individual bands of the base layer comprising the tilted ‘VALID’ elements in green, the transparent revealing layer represented by dashed red sampling lines, and the resulting moiré shape element ‘VALID’ in cyan. A printed example of a 1D moiré at 1∶1 scale can be seen in Figure 1c. Periodic bands, comprising the vertically flattened text ‘VALID’ as the base layer, are superimposed with a revealing line grating with opaque and transparent sections. In the areas where the revealing line grating is superimposed, the moiré formed by the corresponding magnified text can be seen. In the enlarged section, the base band replication vector (tx, ty) and the period of the revealing layer line grating (Tr) are represented.
Linear 1D moirés. (a) Representation of a 1D moiré rectilinear base and revealing (lenticular array) layers. The moiré image is revealed when both elements are superimposed. (b) Schematic view of the moiré shapes (in cyan) generated by the superposition of a base layer with replicated base bands (‘VALID’ in green) and of transparent revealing layer lines (dashed red lines). (c) Example of a base band grating made of a replicated, vertically compressed text (‘VALID’), with the moiré revealed by a transparent line grating (revealing layer).
As described in Supplementary Information 1, the height H of the corresponding moiré can be expressed as:

where ty corresponds to the vertical component of the base band repetition vector (tx, ty). The moiré presented in Figure 1c has been designed with a Tr of 20 pixels and a band repetition vector of (−2, 16) pixels. Hence, the height of the moiré is 80 pixels. Equation (1) shows that if ty<Tr, a positive moiré height is obtained, i.e. both the base band shapes and the moiré shapes have the same orientation. When displacing the revealing layer upwards with respect to the base layer, the moiré shapes move down. On the other hand, when ty>Tr, the moiré height is negative, i.e. base band shapes and moiré shapes have inverse orientations. Moving the revealing layer up has the effect of moving the moiré upwards, and vice versa.
This mathematical model is used here to design two moirés, representing the letters ‘ABC’ and the numbers ‘123’, with ty>Tr and ty<Tr, respectively. In order to observe these moirés with the naked eye their height has been set to H=5 mm. Furthermore, the respective base layouts are reproduced at a print resolution of 9754 dpi. The revealing layer period for both moirés is Tr=62.5 µm, corresponding to a line grating of 160 lines cm−1. The base layer height is ty=63.3 µm for the ‘ABC’ moiré and ty=61.7 µm for the ‘123’ moiré. In both cases the base layer period ty and the revealing layer period Tr are close one to another. Then, as is evident from Equation (1), even a microscopic variation of the base or revealing layer periods results in a macroscopic modification of the height of the revealed moiré images.
The robustness of these high-resolution moirés against counterfeiting attempts is shown further below. Here, we first describe the new concept of curvilinear 1D moirés whose curvilinear layout follows the level lines of a desired continuous function. These curvilinear moirés moving along radial or spiral trajectories offer new, appealing visual effects.
Curvilinear moiré design
The mathematical model that enables deriving the layout of the base layer capable of creating a circular moiré is depicted in Supplementary Information 2. Figure 2 shows an example of a circular moiré designed using this model, as well as its corresponding base layer in the original space and in the circularly transformed space. Figure 2a shows the designed moiré layout in the original space formed by an ‘EPFL’ element laid out horizontally with a replication vector having an oblique orientation. An enlarged section of the base layer corresponding to this moiré is shown in Figure 2b. Conversely, Figure 2c shows the same moiré, but in the circularly transformed space. The desired ‘EPFL’ moiré is laid out along concentric circles. An enlarged section of its corresponding base layer is shown in Figure 2d. The layout of the letters ‘EPFL’ within this base layer is given by the geometric transformation expressed in Supplementary Information 2, Equation (6).
Moiré base and revealing layer fabrication
Moiré base layers with resolutions up to 9754 dpi (corresponding to a pixel size of 2.6 µm) were fabricated by means of an Au lift-off process14 using UV lithography. This is a higher resolution than those achievable with standard printing.
In order to reveal the moiré produced by the high-resolution base layers described above, lenticular arrays with frequencies of 160 lenses cm−1 are required. Such microlenses were fabricated using a soft-lithography technique known as micromolding in capillaries (MIMIC).15,16 MIMIC is a replication technique that requires the use of masters. These masters were fabricated using positive photoresist (AZ9260; MicroChemicals GmbH, Ulm, Germany) and a reflow process.17 Poly-dimethylsiloxane (Sylgard 184; Dow Corning, Midland, MI, USA), was used to obtain the negative of the master. Both sides of the replicated microchannel array are cut open and placed over a transparent substrate. To create the cylindrical lens array proposed here, we selected the negative epoxy-based photoresist, SU-8, since this material exhibits convenient optical and mechanical properties.18 The microchannels are filled with SU-8 by capillary forces. When the channels are fully filled the SU-8 is cross-linked. Finally, the poly-dimethylsiloxane stamp is removed mechanically and the cylindrical microlens array is ready to be used.
Results and discussion
The fabricated base and revealing layer structures were characterized to confirm that they met the design requirements. Figure 3a shows the optical image of a circular 1D moiré base layer with a size of 2 cm×2 cm. No specific design (letters or graphic symbols) can be seen in this image. However, as shown in Figure 3b, when the same base layer is examined with an optical microscope (the dashed rectangle in Figure 3a shows the magnified area) it is possible to see the base layer ‘EPFL’ element, whose layout is determined by the geometric transformation given in Supplementary Information 2, Equation (6). As can be seen, this image is identical to the designed moiré layout presented in Figure 2d. If we magnify this feature (the dashed rectangle in Figure 3b), it is possible to see the exact delineation of its elements and the individual pixels.
Fabricated base and revealing layers. (a) Optical image of fabricated Au base layers on glass substrate for a circular 1D moiré moving along spirals. (b) Magnified microscope image of this base layer corresponding to the dashed square area in Figure 3(a). (c) A more magnified microscope image of the base layer corresponding to the dashed square in Figure 3(b). (d) An optical picture of a bent lenticular array fabricated over a flexible substrate and SEM images of the lenticular arrays fabricated from (e) a commercial master, (f) a positive photoresist master fabricated in our laboratory and (g) a magnified image of the lenses shown in (f).
Due to the versatility of the MIMIC process it was possible to fabricate the lenticular arrays, not only on rigid glass substrates, but also on flexible substrates (biaxially-oriented polypropylene), as shown in Figure 3d. As can be seen, the lenticular array is bent along both the longitudinal axis (parallel to the cylindrical lenses) and the orthogonal axis (perpendicular to the cylindrical lenses). No cracking or adhesion problems were observed after bending the lenticular arrays. Figure 3e shows a scanning electron microscope image of a lenticular array with a period of 179 µm, replicated from a commercial master (NT43-029; Edmund Optics Ltd, Nether Poppleton, UK). Using a fabricated photoresist master, it was possible to fabricate lenticular arrays with a frequency of up to 200 lenses cm−1, corresponding to a period of 50 µm. A scanning electron microscope image of these structures is presented in Figure 3f. As can be seen, the sample copied from the commercial master presents some defects. These defects were already present in the original master and copied during the replication process. On the other hand, the lenticular array obtained from the customized master shows excellent quality, without any defects or roughness, even when it is inspected at higher magnifications, as shown in Figure 3g. Figure 4 shows the contour shape of five lenses in an array of cylindrical lenses with a period of 50 µm. The inlet shows the contour shape of five different microlenses. All the lenses exhibit equivalent contour shapes, resulting in equivalent focal distances. Arrays with focal distances ranging from 45 to 485 µm were fabricated. The diffraction limit of the fabricated lenses ranges between 0.8 and 1.6 µm. Such diffraction limits are smaller than the minimum feature on the base layer, corresponding to 2.6 µm.
The moiré features are characterized by superimposing the base and revealing layers and comparing the resulting moirés with those designed. Figure 5 shows optical images of: (i) a rectilinear 1D moiré with a resolution of 9754 dpi, showing the repeated ‘ABC’ and ‘123’ moiré shapes; (ii) a circular 1D moiré with radial trajectories and a resolution of 5080 dpi showing a ‘star’ feature; and (iii) a circular 1D moiré with spiral trajectories at the same resolution, showing the letters ‘EPFL’. As previously mentioned, it is not possible to directly recognize the image embedded within the base layer, as shown in the top pictures. However, when the revealing layer with the corresponding period (62.5 µm for the linear moiré design at 9754 dpi and 180 µm for both circular moiré designs at 5080 dpi) is correctly oriented over the base layer, the moiré appears and the information embedded within the base layer is revealed, as shown in the bottom images. There is a good match between the designs and the fabricated moirés as can be observed by comparing the moiré designed in Figure 2c and the one presented in Figure 5c. A video of this moiré moving along the spiral trajectories is presented in Supplementary Information 3. Once the base and the revealing layer are superimposed and aligned with less than 1° deviation, the ‘EPFL’ moiré appears. However, when the revealing layer is rotated with respect to the base layer the revealed image is gradually distorted until it completely disappears at 45°. Additionally, when the revealing layer is moved down, the ‘EPFL’ moiré moves away from the central point along a spiral and increases in size. Conversely, when the revealing layer is moved up, the ‘EFPL’ moiré moves towards the centre along a spiral and decreases in size. This expected behaviour demonstrates the validity of the mathematical model developed (Supplementary Information 2) and of the proposed fabrication technologies for both the base and the revealing layers.
High-resolution moirés features. Optical images of the base layers: (a) rectilinear ‘ABC’ and ‘123’ moirés, resolution of 9754 dpi; (b) circular, radial ‘star’ moiré, 5080 dpi; and (c) circular, spiraling ‘EPFL’ moiré, 5080 dpi. Below are corresponding moiré images when base and appropriate revealing layers are super-imposed.
As introduced before, the rectilinear ‘ABC’ and ‘123’ moirés (Figure 5a) were used for determining the robustness of the high-resolution moirés against counterfeiting. Surrogate counterfeit base layers of such moirés were fabricated with different scaling factors, ranging between 96% and 104%. Figure 6 shows the experimental results (squares for the ‘123’ moiré, and circles for the ‘ABC’ moiré) together with the theoretical height of the moiré as a function of the base layer scaling factor. The pictures show the fabricated moirés at the different base layer scaling factors. As can be observed, there is a good agreement between the experimentally measured moiré height and the moiré height calculated according to Equation (1). For a scaling factor of 100% (original moiré designs) both the ‘ABC’ and the ‘123’ moirés have similar sizes, and are upright. Numerically, since (Tr−ty)<0, the ‘ABC’ moiré has a negative height. The corresponding element in the base layer is therefore laid out upside down. Hence, for the moiré with a base layer scaling factor of 98%, the ‘ABC’ moiré is inverted and increases in size, while the ‘123’ feature is reduced in size but keeps its orientation. When the scaling factor is further reduced to 96%, both the ‘ABC’ and ‘123’ features are clearly reduced in size. On the other hand, if the scaling factor is larger than 100%, a similar behaviour is observed, but the ‘ABC’ moiré keeps its orientation, while the ‘123’ moiré is upside down. Hence, a variation of only 2% of the base layer period (equivalent to a variation of 1 µm) results in a drastic macroscopic variation that can be easily recognised without requiring any additional or external elements.
Counterfeiting robustness of high-resolution moirés. Top: optical images of the rectilinear 1D moiré for scaling factors ranging from 96% to 104% of the base layer period. Bottom: graphical representation of both the calculated and experimental height (cm) of the ‘123’ moiré and of the inverted ‘ABC’ moiré as a function of the base layer scaling factor (%).
Conclusions
This paper describes the first use of 1D moirés to create complex moving features with resolutions close to 10 000 dpi. Such moirés were designed, fabricated and characterized for use as esthetic security features. New geometrical transformations were developed to create circularly laid out moiré images. Microfabrication techniques were developed to fabricate the base layer in Au on glass substrates with resolutions of up to 9754 dpi, resulting in a pixel size of 2.6 µm. The features obtained at such a resolution cannot easily be replicated with standard lithography or printing methods. Hence, these base layers are robust against counterfeiting attempts relying on desktop scanners and printers. The corresponding revealing layers, in the form of lenticular arrays, were made by MIMIC using a transparent epoxy polymer over flexible substrates with frequencies up to 200 lenses cm−1. As proof of concept, three different moirés showing different symbols and letters in one single layout were studied: (i) a rectilinear moiré with its elements distributed along parallel horizontal lines; (ii) a moiré with circularly laid out star symbols aligned along radial lines; and (iii) circularly laid out ‘EPFL’ moiré shapes that shift relative to each other according to their distance from the center point, exhibiting new moiré displacement patterns along radial and spiral lines. Such features are of great interest for applications requiring both visual attractiveness and counterfeit prevention elements, such as banknotes, identity cards, watches and luxury articles. Authentication can be performed thanks to structures easily recognizable to the naked eye. In addition, the moiré images created are extremely sensitive to reproduction variations. We specifically demonstrated that microscopic variations (around ±1 µm of the period) result in strong macroscopic changes in the reconstructed moiré images, providing a new and easily identifiable component. This ensures that replication of the 1D moiré elements is very difficult since copies must be perfect at a scale of 1∶1 down to the micrometer range. Furthermore, such copies cannot be easily achieved since the moirés have been fabricated using microtechnologies at resolutions up to 9754 dpi. These features confirm that the high-resolution moirés presented in this work are excellent candidates for providing both improved protection against counterfeits and additional visual attractiveness.
Author contributions
VJC, SC, RDH and JB conceived the proposed high-resolution moirés based on micro-technology fabrication methods; SC and RDH designed the moirés elements and elaborated the mathematical model; VJC and KS fabricated the base layers; VJC fabricated the revealing layers and characterized the moirés elements; VJC wrote the manuscript text supported by RDH and JB. All the authors reviewed and edited the manuscript.
Supplementary Information for this article can be found on Light: Science and Applications’ website (http://www.nature.com/lsa).
References
Amidror I . The Theory of The Moiré Phenomenon. Vol. 1, Berlin: Springer; 2009 .
Righi A . Sui fenomeni che si producono colla sovrapposizione di due reticoli e sopra alcune loro applicazioni. Nuovo Cimento ; 1887/ 22: 10–34.
Oster G, Wasserman M, Zwerling C . Theoretical Interpretation of Moiré Patterns. JOSA 1964; 54: 169–175.
Durelli AJ, Parks VJ . Moiré Analysis of Strain. New York: Prentice-Hall; 1970 .
Post D . Sharpening and multiplication of moiré fringes. Exp Mech 1994; 7: 154–159.
Takasaki H . Moiré topography. Appl Optics 1970; 6: 1467–1472.
Mikami O . New image rotation using moiré lenses. Jpn J App Phys 1975; 14: 1065–1066.
Hutley MC, Hunt R, Stevens RF, Savander P . The moiré magnifier. Pure Appl Optics 1994; 3: 133–142.
Amidror I . A generalized fourier-based method for the analysis of 2D moiré envelope-forms in screen superpositions. J Mod Optics 1994; 41: 1837–1862.
Kamal H, Völkel R, Alda J . Properties of moiré magnifiers. Optical Eng 1998; 37: 3007–3014.
Steenblik RA, Hurt MJ . Unison Micro-optic Security Film. In: van Renesse RL, editior. Optical Security and Counterfeit Deterrence Techniques V. Proc SPIE 2004; 5310: 321–327.
Schilling A, Thomkin WR, Staub R, Hersch RD, Chosson S, Amidror I . Diffractive moiré features for optically variable devices. In:van Renesse RL, editior. Optical Security and Counterfeit Deterrence Techniques VI. Proc SPIE 2006; 6075: 1–12.
Hersch RD, Chosson S . Band moiré images. Proceedings of SIGGRAPH 04, ACM Computer Graphics, Annual Conference Series; 2004: 239–247.
Madou M . Fundamentals of Microfabrication. Boca Raton: CRC press; 1997.
Xia YN, Whitesides GM . Soft lithography. Annu Rev Mater Sci 1998; 28: 153–184.
Llobera A, Wilke R, Johnson DW, Buttgenbach S . Polymer microlenses with modified micromolding in capillaries (MIMIC) technology. IEEE Photon Technol Lett 2005; 17: 2628–2630.
Schilling A, Merz R, Ossmann C, Herzig HP . Surface profiles of reflow microlenses under the influence of surface tension and gravity. Opt Eng 2000; 39: 2171–2176.
Lorenz H, Despont M, Fahrni N, Brugger J, Vettiger P, Renaud P . High-aspect-ratio, ultrathick, negative-tone near-UV photoresist and its applications for MEMS. Sensor Actuat A Phys 1998; 64: 33–39.
Acknowledgements
The authors are pleased to acknowledge the EPFL Center of MicroNano Technology (CMI) for their valuable discussions and help. This work was partially funded by projects 200020-105119/1 and 200021_143501/1 of the Swiss National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Supplementary information
Supplementary information
SI 1: Rectilinear 1D moiré mathematical model (DOC 26 kb)
Supplementary information
SI 2: Curvilinear 1D moiré mathematical model (DOC 283 kb)
Supplementary information
SI 3: Curvilinear 1D moiré moving along spiral trajectories (DOC 26 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Cadarso, V., Chosson, S., Sidler, K. et al. High-resolution 1D moirés as counterfeit security features. Light Sci Appl 2, e86 (2013). https://doi.org/10.1038/lsa.2013.42
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2013.42
Keywords
This article is cited by
-
Combining external attention GAN with deep convolutional neural networks for real–fake identification of luxury handbags
The Visual Computer (2023)
-
Strain-tunable optical microlens arrays with deformable wrinkles for spatially coordinated image projection on a security substrate
Microsystems & Nanoengineering (2022)
-
Design and analysis method of moire magnifier based on depth cues from disparity
Optoelectronics Letters (2019)
-
Dot-Matrix Hologram Rendering Algorithm and its Validation through Direct Laser Interference Patterning
Scientific Reports (2018)
-
Illusions to foil counterfeiters
Nature (2013)