Abstract
From detailed numerical calculations, we demonstrate that in simple photonic crystal structures, a discrete number of Bloch surface-localized eigenstates can exist inside the continuum of free-space modes. Coupling to the free space causes the surface modes to leak, but the forward and back-reflected leakage may interfere destructively to create a perfectly bound surface state with zero leakage. We perform analytical temporal coupled-mode theory analysis to show the generality of such phenomenon and its robustness from variations of system parameters. Periodicity, time-reversal invariance, two-fold rotational symmetry and a perfectly reflecting boundary are necessary for these unique states.
Similar content being viewed by others
Introduction
Soon after the discovery of photonic bandgap materials, it became known that electromagnetic modes could be localized on the surface of a photonic crystal (PhC).1,2 Such a state may exist if it cannot couple to any bulk state in the PhC or to any free-space mode in air; the bandgap of the PhC prohibits propagation, serving the same role as metals and negative-index materials in surface plasmon modes.3 These PhC surface states have been observed experimentally,4,5 and their localized properties have been applied to enhance light collimation6,7 and to manipulate photons on defects of the surface.5 It is often thought that bona fide photonic surface states can only exist below the light cone of the ambient air (i.e., below the continuum of radiation modes in air), where they are confined by total internal reflection. We show that, under appropriate but general conditions, photonic surface states may also exist inside the radiation continuum. Although coupling to radiation modes is allowed, such a state can have an infinite lifetime because different leakage channels interfere destructively to completely cancel each other.
To explain the physical origin of perfect cancellation among different leakage channels, we carry out rigorous analysis using temporal coupled-mode theory, which provides a generic description for coupling between the localized and propagating modes. We find that in addition to periodicity along the surface and a photonic bandgap that perfectly reflects light, the existence of these embedded Bloch surface eigenstates also requires unbroken time-reversal symmetry and a C2 rotational symmetry about the surface normal. The analysis applies to general wave systems, suggesting that this phenomenon may exist beyond optical systems. Such states offer new possibilities that may find use in the design of narrow-band waveguiding structures or in applications where strongly localized fields are desired.
We also note that, a lossless Bloch surface mode inside the radiation continuum falls within a rare class of states known as “embedded eigenvalues”.8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38 Shortly after the emergence of quantum mechanics, von Neumann and Wigner proposed that the single-particle Schrödinger equation may possess spatially localized states lying above the asymptotic limit of the potential and embedded in the continuum of extended states.8 Unlike non-embedded eigenvalues, embedded eigenvalues are typically difficult to find and generally disappear (become resonances) when slightly perturbed. Moreover, the impractical nature of the original proposed artificial Hamiltonians has made experimental verification difficult. For this reason, an embedded eigenvalue in quantum systems has never been demonstrated. The only known attempt concerns an electron bound state lying above the quantum-well potentials of a superlattice heterostructure, but within the bandgap of its mini bands,39 i.e., not an embedded eigenvalue. Thus, theoretical explorations to discover simpler, easily realizable, and more robust systems that can contain embedded eigenvalues are of great interest. Embedded eigenvalues have also been explored in Maxwell’s equations17,18,19,20,21,22,23,24,25,26,27,28,29 and in the acoustic and water wave equations.30,31,32,33,34,35,36,37,38 One occasion is when the spectrum of the problem can be separated by space group symmetry and when an odd-symmetry bound state lies in the continuum spectrum of the even states.17,18,19,20,21,22,23,30,31,32,33,34 Embedded states that do not rely on symmetry separability have received much attention,10,11,12,13,14,15,16,24,25,26,27,28,29,35,36,37,38 but have never been experimentally verified, primarily because they are fragile to perturbations. In this work, we identify theoretically a new realization of an embedded eigenvalue in a PhC system that does not rely on symmetry, yet should be easily realizable. Moreover, we find that unlike most known embedded eigenvalues, the one described here is robust from changes of system parameters; the eigenvalue simply shifts to another wavevector without fading into a resonance (as is characteristic in other embedded eigenvalue systems). The possibility of an embedded eigenvalue in a very similar structure was previously suggested by numerical investigations,40 but without proof or explanation of how such a state might arise.
Surface eigenstate in the continuum
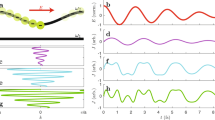
For comparison, we begin with a known example of a PhC surface-mode band structure,1,4 given in Figure 1a, where the PhC is a two-dimensional square lattice of dielectric cylinders. By terminating the surface rods in half on the (100) surface, one creates surface modes in the lowest photonic bandgap of TM modes (where electric field is normal to the plane,  ). These states are on the lowest-frequency band of the surface rods; they lie below the light cone, and do not interact with the continuum of free-space modes. In comparison, higher-frequency bands of the surface rods can be brought into the photonic bandgap of the same bulk PhC by increasing the radii of the surface rods; this band structure is shown in Figure 1b. Here, the second band enters the light cone, where it couples to the radiation modes and becomes leaky. From finite-difference time-domain (FDTD) simulations,41 we excite these resonances with point sources on the surface, and perform harmonic analysis to obtain the lifetime τ and quality factor Q=ωτ/2 of these resonant modes. As shown in Figure 1c, there is a sharp increase of lifetime that approaches infinity when the surface-parallel wavevector is near ky≈0.28×2π/a, with a being the period of the PhC. In other words, there is a discrete point of wavevector where the resonant mode decouples from radiation and becomes an eigenstate. Figure 1d–1f show the field profiles Ez of the surface modes at and away from the peak. There is no leakage to air at the particular wavevector (Figure 1e), in contrast to nearby resonant modes (Figure 1d and 1f) where radiation leakage is clearly visible.
). These states are on the lowest-frequency band of the surface rods; they lie below the light cone, and do not interact with the continuum of free-space modes. In comparison, higher-frequency bands of the surface rods can be brought into the photonic bandgap of the same bulk PhC by increasing the radii of the surface rods; this band structure is shown in Figure 1b. Here, the second band enters the light cone, where it couples to the radiation modes and becomes leaky. From finite-difference time-domain (FDTD) simulations,41 we excite these resonances with point sources on the surface, and perform harmonic analysis to obtain the lifetime τ and quality factor Q=ωτ/2 of these resonant modes. As shown in Figure 1c, there is a sharp increase of lifetime that approaches infinity when the surface-parallel wavevector is near ky≈0.28×2π/a, with a being the period of the PhC. In other words, there is a discrete point of wavevector where the resonant mode decouples from radiation and becomes an eigenstate. Figure 1d–1f show the field profiles Ez of the surface modes at and away from the peak. There is no leakage to air at the particular wavevector (Figure 1e), in contrast to nearby resonant modes (Figure 1d and 1f) where radiation leakage is clearly visible.
Properties of surface modes lying within the radiation continuum. (a and b) Projected band structures for a square lattice (period a) of cylindrical dielectric rods (ε=8.9, r=0.2a) in air, with terminations as shown in the insets. In a, the surface rods are cut in half, while in b, the surface rods have increased radii, rs=0.33a. Gray shaded regions represent the light cone where there is a continuum of radiation modes. The light and dark khaki regions are the projected bulk bands of the photonic crystal. Surface modes that do not couple to radiation are shown as blue lines (these are the well known states) and a blue cross (this is an embedded eigenstate); those that do couple to radiation are shown as a red line. (c) Quality factor Q for the leaky surface modes along the red line in b. At ky=0.2768×2π/a, the lifetime goes to infinity, and the leaky mode becomes an eigenmode. (d–f) Ez field patterns of the surface modes at the specified wavevectors, where kya/2π=0.260, 0.2768 and 0.290, respectively.
This phenomenon can be understood as an interference effect. The surface rods support a localized mode, which leaks to the right into the air (channel one), and to the left into the bulk PhC. Since the frequency of the state is inside the bandgap of the bulk PhC, all the left-going light is reflected, and part of that is transmitted through the surface rods into the air (channel two), interfering with channel one. When waves in these two channels have the same magnitude and differ in phase by π, destructive interference eliminates the radiation loss.
Periodicity is an important ingredient to these unique embedded states. If the structure is uniform in the surface-parallel direction (such as a plain uniform slab next to a uniform bulk structure), then any state within the radiation continuum must be leaky because fields in the air consist of propagating planewaves only. On the other hand, when the structure has periodicity in the surface-parallel direction (y-direction), fields in the air can consist of evanescent fields with any wavevector ky in the reciprocal lattice (i.e., ky’s that differ by integer multiples of 2π/a), so an infinite-lifetime resonance may exist. In the present case, periodicity also gives rise to band folding, which creates the resonant modes we study.
Given periodicity, it still remains to be answered if a perfect cancellation between the forward leakage and the back-reflected leakage can occur at all, and if so, what the other required conditions are. Furthermore, for experimental demonstrations, it is also critical to know whether the occurrence of such unique states is robust from small differences between the theoretical structure and the fabricated structure. In the next section, we carry out an analysis using temporal coupled-mode theory to answer these questions and to explain why such states do indeed exist and should be readily observable experimentally.
Coupled-mode theory analysis
In our intuitive understanding of cancellation, the coupling between the surface mode and the radiating modes is an essential element. Therefore, we apply temporal coupled-mode theory,1,42 which provides a simple analytical description for resonant objects weakly coupled to incoming and outgoing ports. Temporal coupled-mode theory has been widely used in a variety of resonator systems ranging from optical waveguides and cavities, electronic circuits, to mechanical and acoustic resonators. It works well in the weak-coupling regime (when Q=ω0τ0/2>>π); in practice, it is nearly exact when Q>30, which is the case for all examples considered in this work. In our system, ω0 is the frequency of the localized mode, and τ0 is its lifetime when coupled to planewave modes in air (without considering the back-reflection). Inside the bandgap, the bulk PhC reflects all incoming waves. Thus, we treat the bulk PhC as a perfectly reflecting mirror, as illustrated in Figure 2. The amplitude A of the localized mode evolves as dA/dt=(−iω0−1/τ0)A in the absence of input powers. When incoming planewaves are included, the temporal coupled-mode theory equation can be written in Dirac notation as Refs. 1, 42 and 43:
Schematics for the set-up of temporal coupled-mode theory. Inside the bandgap, the bulk photonic crystal reflects all incoming light, so in our analysis we treat the photonic crystal as a reflecting boundary. In temporal coupled-mode theory, the localized mode has amplitude A, which is coupled to the incoming and outgoing waves with amplitudes  and
and  , respectively. Dashed lines indicate the reference planes for the phase of
, respectively. Dashed lines indicate the reference planes for the phase of  .
.


where  and
and  are column vectors whose components s1+, s2+ and s1−, s2−, respectively, are amplitudes of the incoming and outgoing planewave modes as illustrated schematically in Figure 2, and
are column vectors whose components s1+, s2+ and s1−, s2−, respectively, are amplitudes of the incoming and outgoing planewave modes as illustrated schematically in Figure 2, and  and
and  are coupling coefficients between the localized mode and the planewave modes. The matrix C is a scattering matrix that describes the direct coupling between the planewave modes on both sides of the rods. We choose the normalizations such that
are coupling coefficients between the localized mode and the planewave modes. The matrix C is a scattering matrix that describes the direct coupling between the planewave modes on both sides of the rods. We choose the normalizations such that  is the energy inside the rods, and that
is the energy inside the rods, and that  and
and  are the incoming and outgoing powers in the mth planewave mode. The coupling coefficients
are the incoming and outgoing powers in the mth planewave mode. The coupling coefficients  ,
,  and the direct scattering matrix C are not independent; energy conservation and time-reversal symmetry require these coefficients to be related by
and the direct scattering matrix C are not independent; energy conservation and time-reversal symmetry require these coefficients to be related by



as has been shown in Ref. 43.
The localized mode couples to one planewave mode on each side of the rods, with the surface-normal wavevector of the planewave given by  . In the frequency range of interest, higher order diffractions (with ky differ by integer multiples of 2π/a) correspond to evanescent modes with imaginary kx that do not carry outgoing power, so they can be neglected. The reflection from the bulk PhC imposes
. In the frequency range of interest, higher order diffractions (with ky differ by integer multiples of 2π/a) correspond to evanescent modes with imaginary kx that do not carry outgoing power, so they can be neglected. The reflection from the bulk PhC imposes

with ψ being a phase shift. For reflection from the bulk PhC, there is no explicit expression of this phase shift. But for a closely related system where the PhC is replaced with a perfect metal distance l away from the rods, the phase shift is simply ψ=2kxl−π. Also, we write the direct scattering matrix as  where r [r′] and t [t′] are the complex reflection and transmission coefficients on the left [right] side of the rods. In the absence of input power (s1+=0), a stationary state with no leakage (s1−=0) occurs when
where r [r′] and t [t′] are the complex reflection and transmission coefficients on the left [right] side of the rods. In the absence of input power (s1+=0), a stationary state with no leakage (s1−=0) occurs when

This equation is a mathematical translation of the intuitive statement that the forward leakage d1A and the back-reflected leakage teiψs2− cancel each other.
The question remains whether such cancellation can occur generally, and if so, what are the requirements. Assume time-reversal symmetry in the system is unbroken (i.e., negligible absorption, and no magneto-optic effect imposed). Then, the complex conjugate of fields in the direct scattering process  is a solution of the Maxwell’s equations with opposite wavevector,1 namely,
is a solution of the Maxwell’s equations with opposite wavevector,1 namely,  where C′ is the scattering matrix of wavevector
where C′ is the scattering matrix of wavevector  . Further, assume that the structure has twofold rotational symmetry C2 about the surface normal, so that C=C′; in the present example where the z dimension is uniform, mirror symmetry σy is sufficient. These results combine to
. Further, assume that the structure has twofold rotational symmetry C2 about the surface normal, so that C=C′; in the present example where the z dimension is uniform, mirror symmetry σy is sufficient. These results combine to  , and so
, and so  , which gives the Stokes relations
, which gives the Stokes relations  and
and  . The same procedure on the process
. The same procedure on the process  leads to equation (2c), which reduces to
leads to equation (2c), which reduces to  . Combining this and the Stokes relations, we get
. Combining this and the Stokes relations, we get  . In other words, in the presence of time-reversal symmetry and a C2 rotational symmetry about the surface normal, the right-hand side of equation (4) always has unit magnitude.
. In other words, in the presence of time-reversal symmetry and a C2 rotational symmetry about the surface normal, the right-hand side of equation (4) always has unit magnitude.
The left-hand side of equation (4) also has unit magnitude because of the perfectly reflecting boundary. In such case, the magnitude condition is always satisfied, and equation (4) can be reduced to the phase

with n being an integer. In other words, this phase condition, equation (5), is the only requirement for achieving perfect cancellation. Intuitively, it may be understood as a sum of phase shifts, with the first term ψ coming from propagation and reflection, and the second term arg (r−d2t/d1) coming from coupling with the localized mode. A conceptually similar phase-shift equation has been used in the context of metallic nanorod cavity, where the second term is replaced with the phase shift from coupling with surface plasmon.44 Equation (5) comes down to locating where the phase shift crosses integer multiples of 2π. Such an intersection may be located by varying the wavevector ky; it results in discrete states with infinite lifetimes, as we have observed in Figure 1c. Not all bands in the light cone will produce such crossings; for example, our previous reasoning indicates that structures without periodicity cannot support such embedded states, so the phase shift for such structures should never cross integer multiples of 2π. But once a crossing is found, the existence of a root will be robust to changes of system parameters since the perturbation will only shift the intersection to a slightly different wavevector.
We note a subtle but important difference between the embedded eigenvalue we study here and that in most known examples. In most examples, the embedded eigenvalue disappears when the parameters of the system deviates slightly from the designed structure or potential, making it very difficult to observe experimentally. In our case, we are concerned with a family of eigenproblems, with each eigenproblem defined by the wavevector of the system. When the parameters of the system change, the embedded eigenvalue disappears from the eigenproblem of one wavevector, but appears in that of another wavevector. In experiments, states with all wavevectors can be measured, and therefore, this shifting does not prevent us from physically observing such states. Following this reasoning, we can also expect that embedded eigenvalues in other periodic systems such as Refs. 27 and 37 should also be robust to parameter changes.
Lastly, we mention that the lifetime of certain resonant cavities can be increased by optimizing their geometries to cancel the dominant component of the far-field radiation.45,46,47,48 However, the embedded eigenstate described here, though not localized in the surface-parallel direction, achieves complete cancellation, which includes all components of the far-field radiation.
Validation of analysis
The coupled-mode analysis has translated our intuitive picture of cancellation into mathematical statements. Furthermore, it showed that perfect cancellation is possible given time-reversal and C2 symmetries in the system. Next, we compare its quantitative predictions with numerical simulations.
With no input power (s1+=0), equations (1) and (3) have solution A(t)=A(0)exp (−iωt−t/τ) with decay rate

This gives the lifetime τ and quality factor Q of the mode. At the perfect-cancellation points discussed in previous section, τ is infinite; away from these points, τ is finite.
Several reference quantities, the natural frequency ω0, lifetime τ0 and the left/right ratio of the decay rates which we denote as  , are measurable and can also be calculated in FDTD simulations. The direct scattering matrix C may be approximated by treating the surface rods as a slab. With these values known, the coupling coefficients d1 and d2 can be determined from equation (2), and lifetime of the localized mode and the location of the perfect-cancellation point can be evaluated from equations (6) and (5) respectively to yield quantitative predictions. Equation (2c) gives a quadratic equation with two roots
, are measurable and can also be calculated in FDTD simulations. The direct scattering matrix C may be approximated by treating the surface rods as a slab. With these values known, the coupling coefficients d1 and d2 can be determined from equation (2), and lifetime of the localized mode and the location of the perfect-cancellation point can be evaluated from equations (6) and (5) respectively to yield quantitative predictions. Equation (2c) gives a quadratic equation with two roots  ; for rods with mirror symmetry in x direction, we have ξ=1 and r=r′, and these two roots correspond to modes whose Ez are even (d1= d2) or odd (d1=−d2) in x direction.
; for rods with mirror symmetry in x direction, we have ξ=1 and r=r′, and these two roots correspond to modes whose Ez are even (d1= d2) or odd (d1=−d2) in x direction.
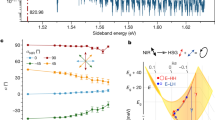
For quantitative validation of these predictions, we consider some explicit examples. First, we consider a simplifying example where the PhC is replaced with a perfect-metal boundary at distance l from the surface rods (Figure 3a inset). In this system, the phase shift at the reflection boundary is simply π, making evaluation of the coupled-mode theory equations easy. This perfect-metal boundary also makes the eigenmodes of this structure equivalent to the asymmetric eigenmodes of a double-column structure (with separation 2l), which has been studied in Ref. 27 with a Fabry–Pérot transmission analysis. Figure 3a shows the band structure for separation l=1.6a. The quality factor Q(ky) of the second band inside the light cone is computed from FDTD simulations and shown in circles in Figure 3b; two infinite-lifetime states corresponding to n=0 and n=1 in equation (5) are observed. Since ψ=2kxl−π, we expect that qualitatively the surface-normal wavevector kx of the infinite-Q states should be inversely proportional to the separation l, which is confirmed in Figure 3c. We also expect that at larger separation, there will be more embedded eigenstates that correspond to phase shifts differing by 2nπ; this is indeed observed in the numerical simulations.
Comparison between FDTD simulations and temporal coupled-mode theory predictions, for a simplified structure where the photonic crystal is replaced with a perfect-metal boundary. Left: data for one column of cylindrical rods with ε=4.9. (a) Band structure for TM modes with l=1.6a. Shaded region is the light cone, states that do not couple to radiation are shown in blue, and states that do are shown in red. The embedded eigenstates are indicated with blue crosses, labeled with the integer n in equation (5). (b) Quality factor Q for leaky modes along the red line in a. Circles are from FDTD simulations, and the red solid line is the prediction from equation (6). The green dashed line shows Q for the same structure without a mirror. (c) Relation between the surface-normal wavevector kx of the embedded eigenstates and the rod-to-mirror distance l. Circles are from FDTD simulations, and lines are predictions from equation (5). Right: (d)–(f) show the same plots as in the left column, but with asymmetric rods as shown in the inset. FDTD, finite-difference time-domain.
For comparison, we evaluate predictions from equations (5) and (6). We approximate the direct scattering matrix C as the TM scattering matrix of a uniform slab with thickness equal to the rod diameter and the dielectric constant equal to a spatial average of the structure. The natural frequency ω0 and lifetime τ0 of the localized mode are calculated from FDTD with only the rods (no mirror). Without the mirror, Ez profile of the band of interest is even in x, so we choose the d1=d2 root. Predictions of equations (5) and (6) are plotted in Figure 3c and 3b, respectively as solid lines. Quantitative agreement between FDTD and the model is observed.
When the separation l is smaller than the rod diameter, we observe some discrepancy between the FDTD results and the model predictions. This is expected, because when the mirror is less than half a wavelength away from the rods, it starts to distort symmetry of the resonance on the rods, and the assumption d1=d2 above is no longer valid. But we note that breaking σx symmetry of the resonance does not suppress the infinite-lifetime state, which is consistent with our coupled-mode theory explanations.
The temporal coupled-mode theory analysis applies to localized modes in arbitrary geometries. To illustrate this point, we consider one more example, where the rods consist of a flat edge and a circular edge, as shown in the inset of Figure 3d. Data for this geometry are shown in Figure 3d–3f. We see that the same features of infinite lifetime occur, demonstrating that the described embedded eigenstates are not sensitive to geometry. Again we evaluate equations (5) and (6) to compare with FDTD, with the only difference being that the decay ratio ξ is no longer unity because the left–right symmetry is broken. The same approximation for the direct scattering matrix C is used, although in this case, there is a small region where no solution of d1 and d2 exists; this is the discontinuity in the red curve of Figure 3f. Again, we observe very good agreement between temporal coupled-mode theory and FDTD.
Lastly, we comment that when reflection on the boundary is not perfect, the lifetime will no longer be infinite but can still be very large. For the structure in Figure 1b with only four periods of small rods in x direction, the finite-sized PhC will allow some light in the bandgap to pass through (intensity reflectance R=0.9998 for the four-period PhC at the wavelength and angle of interest), yet the peak of Q still reaches 6×106. For the structure in Figure 3a and 3b with a plain silver mirror (material ohmic losses included, with complex refractive index from Ref. 49) and assuming periodicity a=300 nm, the first peak of Q (where the mirror has R=0.996) still reaches 2×104, which is 300-times enhancement compared to the no-mirror case. For the second peak, the mirror has larger reflectivity R=0.999 because it is near grazing incidence, and the peak of Q reaches 7×104 (1300-times enhancement).
Conclusions
To summarize, we have demonstrated that surface-localized Bloch eigenstates can exist inside the radiation continuum, without using the symmetry-separability of the spectrum. This is a new class of surface modes, and it can be interpreted as the von Neumann-Wigner states realized in a simple photonic system. Infinite lifetime is achieved by complete cancellation between the two leakage channels, and four ingredients enable this cancellation: (i) periodicity; (ii) time-reversal invariance; (iii) twofold rotational symmetry; and (iv) a perfectly reflecting boundary. These states may be excited for example through near-field coupling either with a prism or with a gain medium in direct contact with the surface. The narrow width of the high-Q state indicates that it may be useful in the design of narrow-band waveguiding structures and single-mode lasers.50,51 As compared to high-Q Fano states at the Γ point,17,18,19,20,21,23 this state offers two unique advantages: (i) the angle at which it occurs is tunable; and (ii) the radiative Q of this state can be tuned to arbitrary values by using a non-perfect reflector or by weakly breaking one of the symmetry requirements. The enhanced lifetime, large surface area and strong localization of these surface states also suggest that they may find use in fluorescence enhancement,52 spectroscopy,53 sensing54 and other applications where strong light–matter interaction is desired. The analysis we perform here with temporal coupled-mode theory treatment is general, and we believe that states similar to those reported in this paper may also be observed in more systems, possibly beyond optics.
References
Joannopoulos JD, Johnson SG, Winn JN, Meade RD . Photonic Crystals: Molding the Flow of Light. Princeton, NJ: Princeton University Press, 2008.
Meade RD, Brommer KD, Rappe AM, Joannopoulos JD . Electromagnetic Bloch waves at the surface of a photonic crystal. Phys Rev B 1991; 44: 10961–10964.
Tsakmakidis KL, Hermann C, Klaedtke A, Jamois C, Hess O . Surface plasmon polaritons in generalized slab heterostructures with negative permittivity and permeability. Phys Rev B 2006; 73: 085104.
Robertson WM, Arjavalingam G, Meade RD, Brommer KD, Rappe AM et al. Observation of surface photons on periodic dielectric arrays. Opt Lett 1993; 18: 528–530.
Ishizaki K, Noda S . Manipulation of photons at the surface of three-dimensional photonic crystals. Nature 2009; 460: 367–370.
Moreno E, García-Vidal FJ, Martín-Moreno L . Enhanced transmission and beaming of light via photonic crystal surface modes. Phys Rev B 2004; 69: 121402.
Kramper P, Agio M, Soukoulis CM, Birner A, Müller F et al. Highly directional emission from photonic crystal waveguides of subwavelength width. Phys Rev Lett 2004; 92: 113903.
von Neumann J, Wigner E . Über merkwürdige diskrete Eigenwerte. Phys Z 1929; 30: 465–467.
Hislop PD, Sigal IM . Introduction to Spectral Theory: With Applications to Schrödinger Operators. New York: Springer-Verlag, 1996.
Stillinger FH, Herrick DR . Bound states in the continuum. Phys Rev A 1975; 11: 446–454.
Friedrich H, Wintgen D . Interfering resonances and bound states in the continuum. Phys Rev A 1985; 32: 3231–3242.
Naboko SN . Dense point spectra of Schrödinger and Dirac operators. Theor Math Phys 1986; 68: 646–653.
Simon B . Some Schrödinger operators with dense point spectrum. Proc Amer Math Soc 1997; 125: 203–208.
Moiseyev N . Suppression of Feshbach resonance widths in two-dimensional waveguides and quantum dots: a lower bound for the number of bound states in the continuum. Phys Rev Lett 2009; 102: 167404.
Krüger H . On the existence of embedded eigenvalues. J Math Anal Appl 2012; 395: 776.
Zhang JM, Braak D, Kollar M . Bound states in the continuum realized in the one-dimensional two-particle Hubbard model with an impurity. Phys Rev Lett 2012; 109: 116405.
Paddon P, Young JF . Two-dimensional vector-coupled-mode theory for textured planar waveguides. Phys Rev B 2000; 61: 2090–2101.
Pacradouni V, Mandeville WJ, Cowan AR, Paddon P, Young JF et al. Photonic band structure of dielectric membranes periodically textured in two dimensions. Phys Rev B 2000; 62: 4204–4207.
Ochiai T, Sakoda K . Dispersion relation and optical transmittance of a hexagonal photonic crystal slab. Phys Rev B 2001; 63: 125107.
Fan S, Joannopoulos JD . Analysis of guided resonances in photonic crystal slabs. Phys Rev B 2002; 65: 235112.
Shipman SP, Venakides S . Resonant transmission near nonrobust periodic slab modes. Phys Rev E 2005; 71: 026611.
Plotnik Y, Peleg O, Dreisow F, Heinrich M, Nolte S et al. Experimental observation of optical bound states in the continuum. Phys Rev Lett 2011; 107: 183901.
Lee J, Zhen B, Chua S, Qiu W, Joannopoulos JD et al. Observation and differentiation of unique high-Q optical resonances near zero wave vector in macroscopic photonic crystal slabs. Phys Rev Lett 2012; 109: 067401.
Čtyroký J . Photonic bandgap structures in planar waveguides. J Opt Soc Am A 2001; 18: 435–441.
Kawakami S . Analytically solvable model of photonic crystal structures and novel phenomena. J Lightwave Technol 2002; 20: 1644.
Watts MR, Johnson SG, Haus HA, Joannopoulos JD . Electromagnetic cavity with arbitrary Q and small modal volume without a complete photonic bandgap. Opt Lett 2002; 27: 1785–1787.
Marinica DC, Borisov AG, Shabanov SV . Bound states in the continuum in photonics. Phys Rev Lett 2008; 100: 183902.
Molina MI, Miroshnichenko AE, Kivshar YS . Surface bound states in the continuum. Phys Rev Lett 2012; 108: 070401.
Shipman SP, Welters A . Resonance in anisotropic layered media. In: Proceedings of 2012 International Conference on Mathematical Methods in Electromagnetic Theory; 28–30 August 2012; Kharkiv, Ukraine; IEEE: Washington, DCUSA, 2012, pp227–232.
Ursell F . Trapping modes in the theory of surface waves. Math Proc Cambridge 1951; 47: 347–358.
Jones DS . The eigenvalues of ∇2μ+λμ=0 when the boundary conditions are given on semi-infinite domains. Math Proc Cambridge 1953; 49: 668–684.
Parker R . Resonance effects in wake shedding from parallel plates: some experimental observations. J Sound Vibrat 1966; 4: 62.
Witsch KJ . Examples of embedded eigenvalues for the Dirichlet Laplacian in perturbed waveguides. Math Methods Appl Sci 1990; 12: 91–93.
Evans DV, Levitin M, Vassiliev D . Existence theorems for trapped modes. J Fluid Mech 1994; 261: 21–31.
Evans DV, Linton CM, Ursell F . Trapped mode frequencies embedded in the continuous spectrum. Q J Mech Appl Math 1993; 46: 253–274.
Groves MD . Examples of embedded eigenvalues for problems in acoustic waveguides. Math Methods Appl Sci 1998; 21: 479–488.
Porter R, Evans DV . Embedded Rayleigh–Bloch surface waves along periodic rectangular arrays. Wave Motion 2005; 43: 29.
Linton CM, McIver P . Embedded trapped modes in water waves and acoustics. Wave Motion 2007; 45: 16.
Capasso F, Sirtori C, Faist J, Sivco DL, Chu SG et al. Observation of an electronic bound state above a potential well. Nature 1992; 358: 565–567.
Shipman SP, Venakides S . Resonance and bound states in photonic crystal slabs. SIAM J Appl Math 2003; 64: 322–342.
Oskooi AF, Roundy D, Ibanescu M, Bermel P, Joannopoulos JD et al. Meep: a flexible free-software package for electromagnetic simulations by the FDTD method. Comput Phys Commun 2010; 181: 687–702.
Haus HA . Waves and Fields in Optoelectronics. Englewood Cliffs, NJ: Prentice-Hall, 1984.
Fan S, Suh W, Joannopoulos JD . Temporal coupled-mode theory for the Fano resonance in optical resonators. J Opt Soc Am A 2003; 20: 569–572.
Ameling R, Langguth L, Hentschel M, Mesch M, Braun PV et al. Cavity-enhanced localized plasmon resonance sensing. Appl Phys Lett 2010; 97: 253116.
Johnson SG, Fan S, Mekis A, Joannopoulos JD . Multipole-cancellation mechanism for high-Q cavities in the absence of a complete photonic band gap. Appl Phys Lett 2001; 78: 3388–3390.
Vučković J, Lončar M, Mabuchi H, Scherer A . Design of photonic crystal microcavities for cavity QED. Phys Rev E 2001; 65: 016608.
Akahane Y, Asano T, Song B, Noda S . High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 2003; 425: 944–947.
Karalis A, Johnson SG, Joannopoulos JD . Discrete-mode cancellation mechanism for high-Q integrated optical cavities with small modal volume. Opt Lett 2004; 29: 2309–2311.
Johnson PB, Christy RW . Optical constants of the noble metals. Phys Rev B 1972; 6: 4370–4379.
Chua S, Chong Y, Stone AD, Soljacic M, Bravo-Abad J . Low-threshold lasing action in photonic crystal slabs enabled by Fano resonances. Opt Express 2011; 19: 1539–1562.
Bravo-Abad J, Joannopoulos JD, Soljačić M . Enabling single-mode behavior over large areas with photonic Dirac cones. Proc Natl Acad Sci USA 2012; 109: 9761–9765.
Hess O, Pendry JB, Maier SA, Oulton RF, Hamm JM et al. Active nanoplasmonic metamaterials. Nat Mater 2012; 11: 573–584.
Le Ru EC, Etchegoin PG . Principles of Surface-Enhanced Raman Spectroscopy: and Related Plasmonic Effects. Amsterdam: Elsevier, 2009.
Lončar M, Scherer A, Qiu Y . Photonic crystal laser sources for chemical detection. Appl Phys Lett 2003; 82: 4648–4650.
Acknowledgements
We thank Dr Ling Lu for helpful discussions. BZ and MS were partially supported by the MIT S3TEC Energy Research Frontier Center of the Department of Energy under Grant No. DE-SC0001299. SLC was partially supported by the MRSEC Program of the NSF under Award No. DMR-0819762. This work was also partially supported by the Army Research Office through the Institute for Soldier Nanotechnologies under Contract No. W911NF-07-D0004.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This work is licensed under the Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Hsu, C., Zhen, B., Chua, SL. et al. Bloch surface eigenstates within the radiation continuum. Light Sci Appl 2, e84 (2013). https://doi.org/10.1038/lsa.2013.40
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2013.40
Keywords
This article is cited by
-
Strong coupling between colloidal quantum dots and dielectric film at room temperature
Applied Physics B (2024)
-
Strong resonance response with ultrahigh quality factor in grating-multilayer systems based on quasi-bound states in the continuum
Scientific Reports (2022)
-
Graphene optical modulators using bound states in the continuum
Scientific Reports (2022)
-
Observation of an Optical Bound State in Photonic Crystal Slabs with U-Shape Nanohole Array
Plasmonics (2022)
-
Flatness and boundness of photonic drumhead surface state in a metallic lattice
Scientific Reports (2021)