Introduction

Since the advent of optical1,2 and holographic3 tweezers the use of optical forces for trapping and propelling microparticles has become widely accepted in areas from physics to biology. In recent years, this field experienced a tremendous development due to the observation of novel mechanisms of light–matter coupling in optically bounded structures and broad application of chip-scale optical devices for particle trapping. The most notable advances include the use of diffractionless and/or engineered optical beams such as Bessel,4,5 Airy,6 optical lattices,7 miniaturized fiber-optics tweezers8 and electromagnetic fields in optically bounded structures.9,10,11 These approaches stimulated observations of optical pulling forces12 and optical lift13 effects. Most recently, near-field optical forces have been explored in the chip-scale optical devices integrated with microfluidic systems. Designs based on nanoplasmonic structures14,15,16 and photonic crystal cavities17,18,19 have been developed for particle trapping.

Studies of optical propelling effects have always been of great interest for potential applications in sorting particles according to their size, index or other properties. The propelling of dielectric microspheres was studied in liquid-immersed evanescent couplers based on dielectric waveguides,20,21,22,23 tapered fibers24 and prisms.25 The light pressure in such structures and devices is determined by the conservation of the total momentum along the propagation direction. It should be noted, however, that due to small reflection and absorption coefficients of dielectric spheres their propelling efficiency is greatly diminished in comparison with estimations made for totally absorbing or mirror-like particles. The propelling velocity normalized by the incident power has been found to be below ∼1 mm s−1 W−1 for dielectric microspheres with diameters (D) from 2 to 20 µm.20,21,22,23,24,25 Propelling efficiencies can be increased for strongly absorbing particles.26 However, in the later case, the dominant mechanism of propelling has been attributed to the photophoretic forces occurring due to non-uniform heating of the light-absorbing particle.

Despite many successes and advancements in this area, one of the most important resources of optical manipulation still remains largely unexplored. It is connected with the use of internal optical resonances in microparticles for enhancing optical forces. Recently, interesting experiments on manipulating polystyrene nanoparticles in a circular motion around silica microspheres have been performed by Arnold et al.27 The optical forces have been resonantly enhanced due to whispering gallery modes (WGMs) in the microspheres; however, the recipient of the optical force, the polystyrene nanoparticle, has been too small to possess resonant properties.

The subject of the present work is connected with a reverse situation when the force is enhanced by the resonance in the moving microsphere. Due to inevitable ∼1% microsphere diameter variations and the size-dependent nature of WGMs resonances, this effect can be used for sorting microspheres with WGM peaks overlapped at the wavelength of the laser source. This is a highly attractive property for fundamental studies and applications of coupled cavity structures and devices.28,29,30,31,32,33 It should be noted, however, that although the resonant forces have been observed in microdroplets by the pioneer of optical tweezers himself, Arthur Ashkin, more than 30 years ago,34 these effects were relatively weakly pronounced. Some evidence for the resonance force enhancement has been obtained in waveguide couplers35 and in the case of off-axially shifted focused beams.36 More recently, the notable advance in this field has been made based on theoretical demonstration of high peak-to-background resonant force ratios in evanescent prism couplers.37,38 However, many properties of resonant light forces still await a thorough investigation.

In the present work, we first present results of our calculation of the optical forces exerted on circular cavities in a simplified two-dimensional (2D) model of surface electromagnetic waves. We show that the resonant forces can approach and even exceed the limits established for totally absorbing particles. After that, we present our experimental observations of propelling of polystyrene microspheres in the near-field vicinity of tapered microfibers immersed in water. For a certain small fraction of spheres with D≈15–20 µm, we observed giant power normalized propelling velocities ∼10 mm s−1 W−1 that exceed the previous measurements in various evanescent couplers20,21,22,23,24,25 by more than an order of magnitude. These extraordinary high propelling efficiencies approach estimations made in a total absorption limit that indicates that a significant part of the total guided power is used for the creating light pressure. We also performed analysis of statistical distribution of the propelling velocities for a large number of microspheres with ∼1% size variations and with mean diameters from 3 to 20 µm. We explain these results using a concept of resonant enhancement of the optical force due to WGM coupling effects. These effects can be used for sorting microspheres with WGM peaks overlapping in the vicinity of the laser source wavelength λ0: Δλ/λ0<1/Q, where Δλ is the WGM peak detuning and Q is the WGM’s quality factor. Taking into account that Q≈103–104 are common for liquid-immersed microspheres,39 it opens up a unique way of selecting the building blocks of chip-scale structures with resonantly coupled WGMs for applications in coupled resonator optical waveguides and coupled cavity devices.

Theoretical modeling of resonant forces

To study the optical forces that can act on WGM resonators we begin with the physical model illustrated in Figure 1a. An initial surface wave with frequency ω is guided by the boundary of the lower half-space with dielectric constant εm<0. The upper half-space has refractive index nb. A dielectric cylinder with refractive index ns is located at a distance d from the boundary. When the surface wave interacts with the cylinder, it can excite the WGMs of the cylinder. The material parameters used in the simulations are εm=−2, nb=1, ns=1.4. Since the material parameters are frequency independent the solution depends only on two dimensionless size parameters kR and kd, where k=ω/c is the wavenumber and c is the speed of light in vacuum. This 2D model captures the basic phenomena important for this study such as the excitation of the WGM by an evanescent tail, the interaction of the excited mode with the guiding structure, and the creation of the scattered field.

Figure 1
figure 1

(a) Schematic of the illumination of a cylinder by a surface wave with the frequency ω guided by the boundary of a half-space with εm<0. The scattering of the surface wave (the typical far field directionality of bulk radiation at resonance is shown in red) creates the propelling force Fx along the surface. (b) Size dependence of the resonant force on the cylinder for various values of the cylinder-boundary separation. (c, top frame) Size dependence of the propelling force on the size parameter kR for the excitation by a surface wave (red curve corresponds to kd=1.5) and by a plane wave (blue curve). (c, bottom frame). Transmittance for the surface wave (olive curve corresponds to kd=1.5).

Full size image

The scattering of a guided wave by a resonator is a complicated diffraction problem. Often this problem is solved by expanding the initial guided wave in terms of the modes of the resonator in free space.40 However, such an expansion is only an approximation and an accurate solution would require the use of the modes of the combined system, e.g., the waveguiding structure and resonator. This approximation is expected to become less accurate as the distance between the resonator and the surface decreases. In our experiments, the separation varied greatly and even reached the values significantly smaller than the wavelength. We therefore resorted to a more rigorous approach that would allow us to obtain accurate results in a wide range of distances.

Our solution is based on the surface potential method41,42,43 applied to the model shown in Figure 1a. We reduce the Maxwell equations to the wave equation for the magnetic field which has only one component oriented along the cylinder axis. Then we express the scattered field outside of the cylinder in terms of the single layer surface potential on the surface of the cylinder and Green’s function for the two half-spaces. The surface potential is expanded in terms of the angular exponential functions. The total field inside the cylinder is expanded in terms of the cylindrical functions. We match the expansions inside and outside the cylinder by using the continuity condition for the magnetic field component and for the tangential electric field component. This matching gives an infinite system of linear algebraic equations for the expansion coefficients. By truncating the system and solving it numerically, we find the coefficients and therefore, the electromagnetic fields inside and outside of the cylinder. In particular, we find the amplitudes of the transmitted and reflected surface waves, as well as the distribution of the far field radiation. The electromagnetic force follows directly from the fields.

We verified the correctness of the numerically calculated fields by checking the balance between the power of the initial surface wave and the sum of powers of the transmitted and reflected waves and the bulk radiation in the far field region. The calculation of force was verified by obtaining an agreement between two approaches: by integrating the Lorentz force (with electric and magnetic components) over the cylinder cross section and by integrating the Maxwell tensor outside of the cylinder.

A plane wave propagating in vacuum and reflected from a mirror creates a force 2P0/c, where P0 is the power incident on a given area.44 In the case of a partial reflection, the force on the mirror will be smaller and, for example, becomes P0/c for a compete absorption. For surface waves, it is therefore instructive to investigate the ratio of the force and the quantity 2P0/c, where P0 is the power of the surface wave, as an indicator of the efficiency of using the surface waves to propel WGM micro-resonators.

A comparison of the force created by a surface wave of power P0 and a plane wave that has power P0 per area of size 2R in the transverse direction is presented in Figure 1c. In both cases, the presence of resonant forces for sizes kR>10 is apparent. For the plane wave, the peak amplitudes and peak-to-background ratios are limited while for the surface wave both the peak amplitudes and peak-to-background ratios increase monotonically with kR reaching extremely high values. The strongly peaked forces correlate well with the dips in the transmittance spectrum for the surface wave. When the transmittance almost vanishes for large values of kR≈30, the normalized force can reach a value around 0.7. This means that the surface wave can propel the transparent cylinder by means of WGM excitation more efficiently than a plane wave can propel a totally absorbing cylinder. For a plane wave in vacuum, such a large value of force would correspond to a significant reflection. For WGM mode, the reflected surface wave is practically negligible and the incident power is distributed between the transmitted surface wave and bulk radiation. A typical example of the far field directionality of bulk radiation is illustrated in Figure 1a. It demonstrates the lobe at ∼57° with the direction of the initial wave propagation, but there is indeed a significant scattering in a range of backward directions at ∼120°–150°. The larger value of force as compared to that for a plane wave can also be attributed to a larger momentum carried by the surface wave.45

The behavior of the resonant propelling force near a selected resonance for various values of distances from the surface is illustrated in Figure 1b. Starting from a large kd>>3 (not shown in Figure 1b), the peak force increases with decreasing kd. The maximum force is obtained at kd≈1.5. The non-monotonic behavior of the magnitude of the optical force at kd<1.5 can be related to interference effects; however, this requires a more detailed analysis. An important consequence for possible optical propelling experiments consists in a substantial overlap of the calculated force peaks for a range of separations 0.15<kd<0.6. A similar peak overlap should take place in the spectral domain for a sphere with kR=29.68−29.69. Once the laser source is tuned into this resonance, the moving particle would experience an enhanced propelling force for a range of separations from the boundary that should simplify the experimental observation of this effect. In principle, similar physical effects take place in various evanescent couplers including dielectric waveguides or tapered fibers.

Materials and methods

Microfluidic fiber-integrated platform

Observation of resonant propelling effects requires the presence of a strong evanescent field in a liquid environment containing microspheres. Tapered microfibers provide a number of advantages compared to other evanescent couplers in such experiments.39 These include small optical losses on the level of a few decibels, natural integration with fiber-optics based light sources and spectrometers, and the possibility to control the flow of the microspheres, as schematically illustrated in Figure 2a. We obtained adiabatically tapered fibers by etching of a single mode fiber SMF-28 in a droplet of hydrofluoric acid.46 This technique allows obtaining tapers with ∼1.5 µm diameters and millimeter-scale lengths. The tapered fibers were integrated with a microfluidic platform fabricated using a Plexiglas frame depicted in Figure 2a. The frame was fixed at the top of the microscope slide to create a microfluidic cell with unrestricted optical access. We selected polystyrene microspheres (Duke Standards* 4000 Series Monosized Particles; Thermo Fisher Scientific, Fremont, CA, USA) for propelling experiments because of their ability to float in water due to the fact that the specific gravity of polystyrene in water is ∼1.05.

Figure 2
figure 2

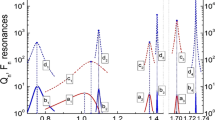
(a) Microfluidic fiber-integrated platform. (b–d) Transmission of 1.5 µm diameter fiber in contact with single water-immersed polystyrene spheres with D=12, 15 and 20 µm, respectively. The WGM polarizations and numbers are labeled. Red and blue curves represent results of fitting with Equation (1). (e) Size dependence of the phenomenological coupling parameters α and κ illustrating weak coupling regime with a critical coupling expected at D≈44 µm.

Full size image

Fiber-taper-coupled microsphere system

Observation of resonant propelling effects also requires efficient WGM coupling determined by the depth of the dip in the power transmission spectra which can be approximated in a single-mode model:47

Here, κ is the coupling constant, β=2πns/λ is the propagation constant (β0=2πns/λ0), ns is the sphere index, α is the field attenuation coefficient inside the sphere, γ is the coupling loss and S=πD is the circumference of the circle in the equatorial plane. In a weak coupling regime (κ<α) which usually takes place for various compact (D<20 µm) water-immersed spheres,39 the depth of the resonant dip in transmission spectra increases with the coupling constant κ.

To identify the range of sphere diameters most suited for observation of resonant propelling effects we determined how both parameters, κ and α, depend on D. This was studied by bringing polystyrene (ns=1.59) spheres in a contact position with the same section of silica taper. Microspheres were individually micromanipulated using a sharpened fiber as a stick. The transmission spectra were measured using a white light source (AQ4305; Yokogawa Corp. of America, Newnan, GA, USA) and optical spectral analyzer (AQ6370C-10; Yokogawa Corp. of America), as shown in Figure 2a.

Figure 2b–d displays a typical evolution of WGM-based coupling features observed in fiber transmission spectra for D=12, 15 and 20 µm, respectively. The spatial WGM properties in microspheres are described by three modal numbers, radial n, angular l and azimuthal m.28,33 The radial number, n, represents the number of the intensity maxima along the radial direction. The angular number, l, shows the number of modal wavelengths around the circumference of the sphere at the equator which can be estimated as πD≈ l(λ/ns). The azimuthal number, m, describes the number of the intensity maxima in a direction perpendicular to the equator according to the formula l−m+1 with the case m=l representing a fundamental mode in the equatorial plane. The azimuthal modes are degenerate in a perfect free-standing sphere. This degeneracy can be lifted by small uncontrollable ellipticity (∼1%) of the real physical beads. The partial overlap of the modes with different m numbers can be responsible for the broadening of the WGM spectral features. It is likely that the dips observed in Figure 2b–d are inhomogeneously broadened due to this effect. Determination of m numbers is not possible in this situation, however n and l numbers as well as the WGMs polarizations, or , can be identified for different dips, as shown in Figure 2b–d. The mode assignment requires fitting the positions of the resonances in a broad spectral range using the Mie scattering theory.39,48

As illustrated in Figure 2e, the fiber-taper-coupled microsphere system operates in a weak coupling regime for spheres with D in 12–30 µm range. Although the maximal resonant optical forces are expected at critical coupling (κ=α) around D≈44 µm, these spheres are too bulky and their narrow first order (n=1) resonances with Q≈105 are difficult to use in practical optical propelling experiments. On the other hand, spheres with 15≤D≤20 µm and Q≈103 provide much better trade-off between their compact dimensions and efficiency of WGM-based coupling. For the 20 µm spheres, the depth of the resonant dips was found to be about 3.5 dB, which means that more than a half of the optical power (∼55%) was transferred into the spherical cavity. Assuming approximately uniform directionality of light scattering, the peak of the resonant force can approach the absorption limit (∼0.55×P0/c) in this case.

Results and discussion

The conventional approach to studying propelling effects is based on using a laser source and an imaging system to visualize light-induced motions of individual particles. The spheres which happen to be in a micrometer-scale vicinity of the evanescent field are attracted to the core by the optical gradient force. After that they can be propelled along the fiber due to the scattering optical forces, as illstrated in the inserts of Figure 3. The particles reach a terminal velocity (v) when the scattering force (Fx) is equal to the drag force, C=6πμRv, where μ is the dynamic viscosity.20,21,22,23,24,25

Figure 3
figure 3

Sequences of snapshots taken with 160 ms time intervals illustrating propelling of polystyrene spheres with different D: (a) 7 µm, (b) 10 µm and (c) 20 µm spheres. Laser light propagates from left to right. Inserts at the top of (a–c) schematically illustrate the type of sphere motion represented by the corresponding consecutive photos. Propelling of 7 µm spheres in (a) is very steady with vmax≈vav. Propelling of 10 µm sphere in (b) shows some variations of the particle velocity. Propelling of 20 µm spheres in (c) demonstrates giant instantaneous velocity between the third and fourth snapshots (counted from top down) reaching vmax≈0.45 mm s−1.

Full size image

Due to the focus of the present study on resonant light pressure effects, we modified the conventional experimental approach to propelling measurements by evanescent fields20,21,22,23,24,25 in regard to the following factors: (i) range of sphere diameters was increased up to 3≤D≤20 µm (compared to previously studied D<10 µm range); (ii) instead of the average propelling velocities (vav=<v>), we measured maximal instantaneous propelling velocities (vmax=max(v)); and (iii) statistical distribution of vmax was studied as a function of D.

Variation of the sphere diameters in a microfluidic platform

Propelling of spheres with different diameters was realized by using a number of suspensions with various mean D values and ∼1% diameter variations in each suspension. A slow flux (∼10 µm s−1) of suspension of microspheres was produced perpendicular to the taper by a micropump (M100; TCS Micropumps Ltd, Ospringe, UK) included in a closed microfluidic loop. Since the parameters of individual tapers such as the thickness of the tapered region were difficult to precisely control, all propelling events were recorded for the same section (∼300 µm length) of the same tapered fiber. After completing measurements for a given sphere diameter the microfluidic platform was cleaned and infiltrated with a suspension containing spheres with different D.

The optical power was coupled from a single mode tunable (1160–1280 nm) semiconductor laser (TOPTICA Photonics AG, Gräfelfing, Germany).49 Due to small scattering losses (∼3 dB) in the tapered region we were able to control the total guided power (P0) at the waist of the taper with ∼5% precision. The propelling velocity is expected to be almost linearly dependent on P0 for spheres with D<10 µm.20,21,22,23,24,25 In order to study the dependence of propelling as a function of D, we fixed the power at the taper waist for all measurements at relatively modest level of P0=43±2 mW. The laser emission linewidth was narrower than 0.1 nm and is smaller than the width of any WGM resonances studied in this work. It was fixed around λ0=1200 nm, and the results did not strongly depend on the selection of λ0. In our experiments variation of the detuning, Δλ=λ−λ0, between the laser emission and WGM resonances (λ) was realized due to random ∼1% deviations of the sphere diameters.

It should be noted that the spheres tend to be separated from the fiber by a nanometric gap occurring due to the double layer repulsive forces between the similarly charged particle and fiber.22 The origin of this gap has been studied in experiments on a WGM carousel, a photonic mechanism for trapping polystyrene nanoparticles in a circular motion around silica microspheres.27 It has been demonstrated that the particle is radially trapped due to a combination of a long-range attractive interaction and a short-range repulsive interaction. The attractive optical force originates from the radial gradient of the evanescent fields. The repulsive electrostatic force is connected with similarly (negatively) charged bare surface of the silica fiber and polystyrene nanoparticles. The average gap sizes have been estimated to be around 35 nm.27 In our work, we used significantly larger polystyrene microspheres. It is likely that in the course of propulsion the radial gap sizes can vary in a certain range that can lead to a variation of the optical force. In addition, the average size of this gap should depend on P0, D, and on the concentration of ions in a suspension. It is likely that the average size of these gaps in our experiments was on the scale of few tenths of nanometers;22,27 however, additional studies are required for more precise characterization of the gap sizes. This plays a critical role in achieving steady propelling along the fiber, because the spheres were covered with a sticky surfactant layer by the manufacturer and physical contact with the fiber would retard their motion. It should also be noted that the small nanoscale gap sizes expected in our case mean that we can use fiber transmission spectra obtained in contact with sphere (Figure 2) for qualitative understanding of the possible role of WGM coupling effects in the course of propelling.

Velocity measurement

The radiative pressure effects were studied by recording movies50 of individual propelling events for each D in inverted microscope (IX71; Olympus America Inc., Center Valley, PA, USA) using CCD camera (Olympus MicroFire; Olympus America Inc., Melville, NY, USA). The frames were sufficiently short (∼5 ms) to represent the snapshots of the spheres’ motion. They were separated by ∼160 ms time intervals.

Typical propelling effects for spheres with D=7, 10 and 20 µm are represented by consecutive photos in Figure 3a–c, respectively. The sequence of snapshots taken for the 7 µm spheres shows motion with constant velocity, as illustrated by dashed construction lines in Figure 3a (a video of the propelling 7 µm spheres is provided in Supplementary Movie 1). We found that propelling with constant velocity was typical for each sphere size in the range 3≤D≤7 µm; however, the velocity is higher for larger spheres. After propelling over a distance on the order of 100 µm (or longer in some cases), the spheres eventually depart the fiber. This can happen due to fluctuations in the liquid flux or due to moving to a wider section of the taper where the evanescent fields are weaker. The motion of 10 µm spheres is less steady demonstrating deviations of the ‘instantaneous’ velocity measured between neighboring frames from the velocity averaged over several frames, as seen in Figure 3b. The particles can also spiral along the taper in some cases, as can be also seen in Figure 3b.

For 15≤D≤20 µm spheres, the variations in instantaneous velocity becomes a dominant factor, as illustrated for D=20 µm in Figure 3c (a video of the propelling 20 µm spheres is provided in Supplementary Movie 2). The likely explanation for this effect is connected with the fact that larger (and more massive) particles have an increased probability of touching the fiber causing the sphere to brake. There might also be other reasons for the seemingly discontinuous motion of the larger spheres based on rapidly varying resonant effects. It is likely that the spheres are rotating along their own axis in the course of the propelling. This can lead to coupling with azimuthal modes with varying m numbers which can be split in energy due to uncontrollable ellipticity (∼1%) of the real physical beads. The variations of the gap sizes can be another reason for discontinuous motion of the larger spheres.

Since we are interested in unrestricted motion of spheres in situations where the light-pressure effects are maximally pronounced, we analyzed long propelling movies to find the maximal velocity measured between neighboring frames, vmax, for each propelling event. In the example shown in Figure 3c such maximal velocity is evident due to ∼70 µm jump of 20 µm sphere between third and fourth frame leading to extraordinary high value of vmax≈0.45 mm s−1. Such vmax reaches ∼60% of the terminal velocity estimated in the total absorption limit: v=P0/(3πcμD)≈0.76 mm s−1. In units normalized by the optical power the measured velocity corresponds to ∼10 mm s−1 W−1 which exceed previously published data for different evanescent couplers20,21,22,23,24,25 by more than an order of magnitude. Taking into account that conventional optical forces on transparent microspheres cannot exceed a few percent of the force estimated in the total absorption limit, the only plausible explanation for the observed extraordinarily high velocities is based on the mechanism of resonantly enhanced optical force.

Statistical properties of propelling

The dramatic difference in propelling of small, 3≤D≤7 µm, and large, 15≤D≤20 µm, particles is illustrated in a greater detail by vmax measurements for a broad range of mean sphere diameters represented in Figure 4a. For each mean sphere diameter the measurements were repeated for many spheres with ∼1% diameter variations. The purpose of these studies was to see how this size disorder would translate into the distribution of propelling velocities. It is seen that for small spheres the velocity is well reproducible for each mean diameter (D=3, 5 and 7 µm) irrespective of the ∼1% size variations. In this range of sphere sizes, we found almost linear dependence of vmax on the sphere diameter in agreement with the previous studies performed in waveguide couplers.20,21,22,23,24,25 The linear dependence can be understood due to the fact that the nonresonant scattering force is proportional to the interaction volume, whereas the drag force is proportional to the sphere cross-section.

Figure 4
figure 4

Results of multiple measurements of (a) maximal instantaneous propelling velocity (vmax) and (b) normalized propelling force (Fx/(P0/c), where Fx=3πμDvmax) for polystyrene spheres with different mean diameters, D=3, 5, 7, 10, 15 and 20 µm. For each mean diameter up to 20–40 measurements were performed using spheres with random ∼1% diameter variations.

Full size image

For large spheres with 15≤D≤20 µm multiple measurements revealed extremely broad vmax distribution in striking contrast with the case of small spheres. Such behavior is expected for resonantly enhanced forces. As illustrated in Figure 2c and d, the WGM resonances with Q≈103 are well pronounced for such spheres. If the laser wavelength matches the position of the WGM resonance, the propelling force should be resonantly enhanced due to a mechanism illustrated for a simplified 2D model in Figure 1b and c. On the other hand, the nonresonant propelling forces (laser line is between the WGM peaks) tend to vanish for sufficiently large circular cavities. Random ∼1% diameter variations should lead to a broad (∼10 nm) distribution of detuning between the laser and WGMs in different spheres. Only a small fraction of spheres with WGM peak position overlapped with the laser line are expected to be propelled along the fiber. For these spheres, the optical forces are expected to display dramatic variations from sphere to sphere depending of the precise amount of small detuning (below ∼1 nm) between the laser and WGMs peak positions. This should lead to a broad distribution of velocities vmax and scattering forces Fx for large spheres, consistent with the results presented in Figure 4a and b, respectively.

To study the transition from nonresonant to resonant propelling effects in a greater detail, we analyzed probability distribution histograms for vmax values measured for multiple spheres with ∼1% size variations, as illustrated in Figure 5. The maximum of the distribution histogram was normalized. For small spheres with 3≤D≤7 µm the histograms represent relatively narrow Gaussian-like distributions with ∼15% standard deviation, as shown in Figure 5a–c. For 10 µm spheres, the distribution becomes much broader which can be interpreted as being due to the onset of resonant propelling effects. For 15 and 20 µm spheres, the distributions become extremely wide demonstrating velocities varying for different spheres by a factor of 4 and 6 in Figure 5e and f, respectively. It should be noted that, due to limited experimental statistics and a somewhat arbitrary determination of the maximal propelling velocity from the experimental movies, the shape of these distributions is not precisely defined in Figure 5e and f. It is apparent, however, that the width and shape of these distributions is strikingly different from the narrow Gaussian-like distributions observed for small spheres, indicating that they are determined by the resonant optical forces.

Figure 5
figure 5

Probability distribution histograms for vmax values measured for spheres with different mean diameters D: (a) –3 µm, (b) –5 µm, (c) –7 µm, (d) –10 µm, (e) –15 µm, (f) –20 µm. For each mean diameter up to 20–40 measurements were performed using spheres with random ∼1% diameter variations. The fitting curves in a–c are represented by normalized Gaussian probability density distributions, f≈exp[(vmax–vmax0)2/2σ2], where vmax0 is the average vmax and σ is the standard deviation. It is seen that for small 3≤D≤7 µm spheres the distributions have Gaussian shape with narrow width σ/vmax0≈15%. For large 15≤D≤20 µm spheres the distributions are extremely wide. The case of 10 µm spheres can be considered as a transitional between these two situations.

Full size image

Such a significant increase of vmax in resonant cases can be used for developing devices capable of sorting microspheres with WGM peaks overlapped with the laser wavelength λ0, Δλ/λ0<1/Q. Taking into account ∼1% diameter variations in the initial suspensions, the resonant WGMs in thus selected spheres might have different angular l numbers; however, such WGMs can still be efficiently coupled51 in structures and devices formed by multiple spheres in a contact position.

Conclusions

We experimentally observed giant optical propelling velocities of 15–20 µm polystyrene microspheres in evanescent fiber-to-microsphere couplers. The normalized propelling velocities measured in our work ∼10 mm s−1 W−1 exceed previous observations20,21,22,23,24,25 by more than an order of magnitude. The magnitude of the corresponding forces reaches 60% of maximal possible force in the total absorption limit. We interpret these observations by resonant enhancement of the optical force due to evanescent coupling to WGMs in microspheres. This interpretation is consistent with our numerical estimations of the peak forces in a simplified 2D model of surface electromagnetic waves evanescently coupled to circular cavities. It is also supported by the statistical analyses of the propelling velocity measurements performed for multiple spheres with ∼1% size variations and with different mean diameters.

These effects can be used for sorting cavities with WGMs peaks which are resonant with the wavelength of the laser source within ∼1/Q relative accuracy. By using a tunable laser the spheres with the desired positions of WGM peaks can be selected. Depending on the application, the method of sorting cavites by using resonant light pressure can be a much more accurate and flexible technique compared to standard in-plane fabrication of coupled microrings and microdisks.52 Microspheres with resonant WGMs can be used as building blocks of delay lines,30 ultra-narrow spectral filters, laser-resonator arrays,53 waveguides,29,30,31,32 focusing devices,54,55 microspectrometers56 and sensors.57 Such spheres are also required in biomedical applications58 where they are used as markers, fluorescent labels and spectral fingerprints.