Abstract
Scatterometry is a well-established, fast and precise optical metrology method used for the characterization of sub-lambda periodic features. The Fourier scatterometry method, by analyzing the Fourier plane, makes it possible to collect the angle-resolved diffraction spectrum without any mechanical scanning. To improve the depth sensitivity of this method, we combine it with white light interferometry. We show the exemplary application of the method on a silicon line grating. To characterize the sub-lambda features of the grating structures, we apply a model-based reconstruction approach by comparing simulated and measured spectra. All simulations are based on the rigorous coupled-wave analysis method.
Similar content being viewed by others
Introduction
The term scatterometry is a general term for a variety of methods that are used to analyze the diffraction spectrum from illuminated samples. The unknown structure parameters are reconstructed by the comparison of measurements and simulations. The most used configurations are normal-incidence reflectometry, spectroscopic ellipsometry, 2-Θ scatterometry and angle-resolved Fourier scatterometry. Raymond has given a comprehensive overview of different scatterometry configurations.1,2
While only one incident/reflected angle is analyzed for most configurations, in Fourier scatterometry, the angular response coming from the sample is measured at the Fourier plane (also called the pupil plane), where it is spatialized. This means that every incident and azimuthal angle corresponds to one specific position in the pupil plane,3 and the whole angular spectrum is recorded in one shot without the need for any mechanical scanning. The Fourier scatterometry method is well suited for the challenging task of profile metrology of very small periodic structures or even for line edge roughness (LER) detection in modern semiconductor applications.4,5,6,7
Because additional depth sensitivity for nanostructures is often required, a combination of profile-sensitive Fourier scatterometry with white light interferometry, which takes advantage of the superior subnanometer resolution for topographic measurements, has been studied. de Groot et al.8,9 showed that imaging the pupil plane makes it possible to measure the incident angle-dependent angular response. In addition, performing a Fourier analysis of the white light signal even facilitates wavelength-dependent ellipsometric measurements with only one measurement. While they use a Mirau- and Michelson-type interferometric implementation, we have chosen the Linnik-type interferometer. This enables us to use a larger numerical aperture (NA=0.95 in our experiment) to collect the diffraction spectrum for higher angles in the pupil plane. The trade-offs of this approach include higher calibration demands and a less compact design that is also more sensitive to environmental influences such as vibrations.
In a previous simulation-based work,10 we compared Fourier scatterometry with our combined white light interference Fourier scatterometry method in terms of sensitivity and correlations with the aim of obtaining different parameters of interest. Since then, we have improved the experimental setup and now show the applicability of the method for real metrology tasks exemplified by the measurement and reconstruction of a silicon line grating profile.
White light interference Fourier scatterometry
Principle
The white light interference Fourier scatterometry setup is based on a typical Fourier scatterometer. Instead of monochromatic illumination, the sample is illuminated using a broadband white light source. Additionally, a reference branch including a reference mirror for white light interference is introduced. The interfering pupil images from the object and reference branch are imaged with a Bertrand lens on a CCD camera. For reconstruction of the structure profile, a comparison between measured and simulated pupil images for each z-position of the scanned reference mirror is performed until the best match is found. This comparison is part of the strategy to solve the inverse problem explained in the next section.
Solving the inverse problem by model-based feature reconstruction
To solve the ill-posed inverse grating problem, a maximum amount of information is needed.11 The systematic combination of a measurement (indirect path) and a model-based simulation (direct path) is a valuable reconstruction strategy to solve this problem. As in our scatterometry applications, we address optically unresolved features, and the information obtained by the high-accuracy measurements is not enough to directly characterize the structures; additional a priori information is needed. These data are calculated by the simulation of the light–structure interaction for all relevant measurement constellations. To accomplish this task, rigorous simulation methods such as the rigorous coupled wave analysis (RCWA) theory are used. The starting point for these simulations is a physical model  of the measurement process, where
of the measurement process, where  represents the measurement condition for the ith data point and
represents the measurement condition for the ith data point and  contains the model parameters (e.g., critical dimension (CD), height, side wall angle (SWA), etc.). All known influences that contribute to the formation of the measured quantity have to be taken into account; this includes the light source, instrument transfer function,12 aberrations and sensor features. Having a simulation model of the measurement system makes it possible to create a database filled with templates that represent different measurement configurations (
contains the model parameters (e.g., critical dimension (CD), height, side wall angle (SWA), etc.). All known influences that contribute to the formation of the measured quantity have to be taken into account; this includes the light source, instrument transfer function,12 aberrations and sensor features. Having a simulation model of the measurement system makes it possible to create a database filled with templates that represent different measurement configurations ( ) or variations in the structure parameters (
) or variations in the structure parameters ( ). This simulation branch is the solution of the direct problem. In contrast, the real measurement of the object delivers data that have to be compared with the calculated templates. Performing a library search by minimizing the distribution:
). This simulation branch is the solution of the direct problem. In contrast, the real measurement of the object delivers data that have to be compared with the calculated templates. Performing a library search by minimizing the distribution:

which depends on the measured ( ) and simulated data (
) and simulated data ( ) contained in the library, making it possible to find the parameters
) contained in the library, making it possible to find the parameters  that yield the minimum
that yield the minimum  . The equation contains the standard deviations
. The equation contains the standard deviations  . The measurement uncertainty can be caused by several error sources: the measurement noise, and systematic and statistical errors.13 The library search makes it possible to identify the object features
. The measurement uncertainty can be caused by several error sources: the measurement noise, and systematic and statistical errors.13 The library search makes it possible to identify the object features  within a specific uncertainty region
within a specific uncertainty region  around the real parameter values
around the real parameter values  that cannot be measured directly with traditional optical methods. Before running such a feedback loop, it is recommended that a sensitivity analysis be performed to learn about the impact of different system parameters and detect the most sensitive measurement configurations.5,14 The general strategy of such a model-based identification technology is shown in Figure 1.15,16
that cannot be measured directly with traditional optical methods. Before running such a feedback loop, it is recommended that a sensitivity analysis be performed to learn about the impact of different system parameters and detect the most sensitive measurement configurations.5,14 The general strategy of such a model-based identification technology is shown in Figure 1.15,16
As mentioned before, the noise and the limited information obtained from real measurements lead to uncertainty ( ) in the reconstructed parameters. To keep this difference smaller than the aspired uncertainties, both an improvement of the physical model used for the simulations and optimized measurement conditions are needed. Such a complex reconstruction can be regularized by the systematic addition of new data taken from other information channels of the optical field,17,18 which is similar to the polarization information, phase data, spectral data, etc. This is precisely the aim of our combined white light interference Fourier scatterometry technique. It combines polarization information, a wide range of incident angles and phase information obtained by shifting the z-position of the reference mirror. Both branches together, the simulation and the measurement branch, offer an elegant approach for solving the inverse problem of reconstructing structure parameters that cannot be observed directly.
) in the reconstructed parameters. To keep this difference smaller than the aspired uncertainties, both an improvement of the physical model used for the simulations and optimized measurement conditions are needed. Such a complex reconstruction can be regularized by the systematic addition of new data taken from other information channels of the optical field,17,18 which is similar to the polarization information, phase data, spectral data, etc. This is precisely the aim of our combined white light interference Fourier scatterometry technique. It combines polarization information, a wide range of incident angles and phase information obtained by shifting the z-position of the reference mirror. Both branches together, the simulation and the measurement branch, offer an elegant approach for solving the inverse problem of reconstructing structure parameters that cannot be observed directly.
Model-based simulation
Simulation of the white light interference Fourier scatterometry technique is performed with our simulation tool, MicroSim.19 It is based on the RCWA20,21,22 for diffraction from arbitrary three-dimensional structures23 and includes some improved convergence methods.24
To simulate white light, it is necessary to calculate the diffraction spectrum for every wavelength. Our illumination has a spectrum of approximately 400–800 nm, which is modeled with a spacing of 10 nm in our simulations. The extended illumination pupil is modeled by planar waves emerging from a quadratic grid, which is sampled with equidistant points corresponding to the different incident angles. Due to the symmetry of the studied structure, only one-quarter of the pupil was simulated. This quarter was sampled by a 35×35 grid. The points are defined by their NA coordinates, NAx and NAy, with  . For each of these points, the diffracted spectrum from the sample is calculated.
. For each of these points, the diffracted spectrum from the sample is calculated.
The reference branch is included in the simulation using Jones-Matrix calculus for the reference mirror. The variable position of the reference mirror during a z-scan is taken into account using a phase term corresponding to the additional path difference.
Additionally, the spectral intensity distribution of the white light source and the spectral sensitivity of the CCD camera are considered for the simulations. The reference mirror reflectivity is modeled using the Fresnel equations.25 Aberrations of the optical elements in the system are unaccounted for at the moment but will be considered in a future version.
Finally, to obtain the resulting pupil images for every z-position, the fields for every wavelength and every incidence angle are incoherently superposed. Additionally, the reference contribution is coherently added for each point. The z-scan itself is simulated for positions of the reference mirror from −150 to 150 nm in 10-nm steps; hence, 31 pupil images are calculated in total. The analyzed periodic grating is modeled with a staircase approximation (see Figure 2) using the following parameters: height, CD and SWA.
Experimental realization
In the following section, we describe our experimental realization of the setup, which is shown in Figures 3–4.
The illumination is accomplished by using a broadband white light source. In our case, we use a white light laser (Leukos SP-UV-8-OEM). This allows us to obtain higher intensity and a more flat intensity distribution for the wavelength range than can be obtained by using a white light LED. A heat-protection filter is introduced to reduce the white light spectrum to the visible range of approximately 400–800 nm, because the optical elements used have the best chromatic aberration corrections in this range. First, we collimate the light coming out of the white light laser fiber. Because the mentioned white light laser has an LP11 mode, we have to homogenize it with the help of two microlens arrays to obtain a homogenous beam distribution.26 We use a rotating dispersion plate to generate a diffuse and homogenous light distribution for our Köhler illumination of the sample and at the same time to obtain a uniform light distribution in the pupil plane that will be imaged. The light then enters a modified Leica DMR microscope in which a beamsplitter separates the light for the object and an optional mounted reference branch. The reference branch consists of a Linnik-type interferometer setup, which is needed to attain the high numerical aperture of 0.95 of the microscope objectives (Leica, PL APO 250×/0.95). The high NA of 0.95 is used to achieve incident angles of up to  . The reference mirror is positioned (z-scan) with the help of a piezo actuator. Finally, the interfering pupil planes of the reference and object branches are imaged with a Bertrand-type lens onto a Frame-Transfer CCD (C8000-10, Hamamatsu Photonics K. K., Hamamatsu, Shizuoka, Japan). Images are taken during a z-scan of the reference mirror.
. The reference mirror is positioned (z-scan) with the help of a piezo actuator. Finally, the interfering pupil planes of the reference and object branches are imaged with a Bertrand-type lens onto a Frame-Transfer CCD (C8000-10, Hamamatsu Photonics K. K., Hamamatsu, Shizuoka, Japan). Images are taken during a z-scan of the reference mirror.
Reconstruction
The reconstruction is performed by a library search. First, a library is created by simulation. The foreknown nominal structure values are selected and the parameters of interest are varied around their nominal values. The measurement is then compared with this library, and the best agreement yields the result of the reconstruction of the structure parameters. For the white light interference Fourier scatterometry, a complete z-scan from −150 to 150 nm of the reference mirror is compared with the simulation.
The function F to be minimized to find the best match is defined by:

The simulated intensity  of the ith pupil point at the z-position j is compared with its equivalent measured intensity
of the ith pupil point at the z-position j is compared with its equivalent measured intensity  . The formula calculates the root mean square error between each simulated and measured pupil (containing N pupil points i) for every z-position j. The sum of these errors for the whole scan is then normalized by the number of pupil images (L) contained in a z-scan.
. The formula calculates the root mean square error between each simulated and measured pupil (containing N pupil points i) for every z-position j. The sum of these errors for the whole scan is then normalized by the number of pupil images (L) contained in a z-scan.
In the future, reconstruction methods other than the very basic minimization of the function F by performing a straightforward library search should be taken into account. Raymond et al.27 made a helpful comparison of the application of standard optimization algorithms to scatterometry.
Measurements and reconstruction
Fourier scatterometry on plain silicon
To check the validity of the measurements, we first measure the pupil image for white light Fourier scatterometry without the reference path. To do this, a nonstructured plain silicon wafer was used as the object. The resulting measured pupil image was compared with the simulated one for s- and p-polarization. The comparison for both polarizations can be found in Figure 5. A perfectly flat native silicon oxide layer with a 3-nm thickness on top of the silicon was assumed for the simulations, which is known from ellipsometric measurements. The other parameters used for the simulation are explained in the simulation section.
Comparison of simulated and measured white light Fourier scatterometry pupil images for s- and p-polarization for a measurement on a plain silicon wafer with a native oxide layer that is 3 nm thick. The maximum intensity is normalized to one in both cases, and the pupil itself corresponds to a numerical aperture of 0.95.
There is good agreement between the measurements and the simulation, although there are still some minor differences. The root mean square error calculated from the difference between the measured and simulated normalized intensity of the pupil-points is 0.12 for the p-polarization case and 0.14 for the s-polarization case. The difference is most likely due to aberrations in the optical system, which are not yet fully quantified and included in the simulation model. This assumption is also supported by the fact that the differences increase toward the outer part of the pupil, which corresponds to higher angles; this indicates the presence of spherical aberrations. In principle, the pupil images on plain silicon represent the dependence of the reflectivity of silicon on the incident angle, which can also be calculated analytically with the Fresnel equations.25 However, the wavelength dependency of the complex refractive index of the materials should be taken into account.
White light interference Fourier scatterometry on a silicon line grating
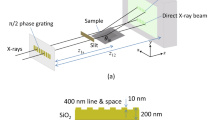
To compare the simulation results for the white light interference Fourier scatterometry, we have chosen an etched silicon line grating. It has a nominal CD of 200 nm and a period of 400 nm. Because we are illuminating with white light from 400 to 800 nm, this structure is in the sub-lambda regime.
Reference measurements
To obtain an impression of the actual shape of the structure, we measured it with an atomic force microscope (AFM) and with a scanning electron microscope (SEM). The results can be found in Figure 6 and Table 1. The SEM image shows that the structure suffers from LER, which is not taken into account in the simulations. Methods that can be used to model LER with RCWA can be found in Refs. 28 and 29. For the AFM results, the fact that the angle of the tip prevents exact measurement of the sidewalls must be taken into account. The real values for the SWAs, rounding and CDs extracted from the AFM profile can differ from the real ones, while the values for the pitch and height are not affected.
Measurement and structure reconstruction
For the actual reconstruction, we computed a library including the variations of the parameters around the values obtained from the AFM and SEM measurements. The library was computed for mid-CD values from 160–200 nm in 1 nm steps, the height was varied from 65 to 95 nm in 1 nm steps, and the SWA was varied from 74 to 85° in 0.5° steps. Rounding was also taken into account. However, the sensitivity was significantly lower compared with the other parameters, so rounding did not have an impact on the reconstruction results. Again, a native silicon oxide (SiO2) layer that was 3 nm thick was included. The typical cross-section model used for the simulation of the structure can be found in Figure 2.
Performing a library search and searching for the minimum of the function F of Equation (2) yields the parameters shown in Table 2 for the reconstructed structure. The corresponding comparison of the 31 simulated and measured pupil images for the z-scan of the reference mirror from −150 to 150 nm in 10 nm steps is shown in Figure 7 for p-polarized light. We only show 30 images (−150 to 140 nm) to obtain an even number of images in the figure.
Measured and simulated pupil images (p-polarization) for a z-scan of the reference mirror from −150 to 150 nm in 10 nm steps for the silicon grating with CD=200 nm. For the top-left pupil image, the optical path difference between the object and reference beam was −150 nm, and for the bottom-right one, it was +140 nm. CD, critical dimension.
The results for the reconstructed profile parameters are in good agreement with the reference measurements obtained with AFM and SEM, although the height is at the upper limit. However, one should keep in mind that scatterometry always integrates over the complete illuminated area (multiple periods of the line grating), while SEM and AFM always yield results at the chosen measurement site. Especially when the structure suffers from LER, there can be differences in the values obtained by direct measurement methods compared with the integrated values obtained from our model-based measurement technique, which at the moment does not take into account LER effects. The minimum value for the function F (Equation (2)) is 0.065. The highest values of F in the library is approximately 0.15. The root mean square (RMS)−error value between the measured and simulated pupil images for this best-matching scan is 6.5%, corresponding to the minimum F value. More details about the calculation of the root mean square value are given in the section on ‘Fourier scatterometry on plain silicon’. The errors in the reconstructed values also depend on the sampling of the library for the parameter of interest. The remaining difference is most likely caused by additional aberrations not yet taken into account in the simulation model and line edge roughness effects.29
Discussion
Because the presented method itself is based on classical scatterometry methods, its performance and usability have to compete directly with these methods. The most used scatterometry measurement configurations are spectroscopic ellipsometry, 2-θ scatterometry and Fourier scatterometry.
For spectroscopic ellipsometry, a fixed angle of incidence is chosen and the wavelength is varied while the ellipsometric angles (Δ,Ψ) or related quantities are measured at the position of the 0th diffraction order. In contrast, for 2-θ scatterometry, the wavelength is fixed and the incidence angle θ is varied while measuring the diffraction efficiency of the 0th order. Because both of these methods only use a subset of the possible illumination/measurement angles compared with Fourier scatterometry measurements in which the illumination and measurement are performed through a high-NA microscope objective, the resulting measurements contain less information. However, the computational effort for these two methods is significantly lower, because each incident direction and each wavelength correspond to one incident plane wave for which the diffraction problem has to be calculated with the RCWA method.
A simulation-based comparison of the sensitivity of Fourier scatterometry with our method has been presented earlier.10 The results show that the addition of the white light interference method makes it possible to obtain a higher or comparable sensitivity for the analyzed samples and less correlation between the parameters of interest in the presence of a reflective substrate. The computational effort using Fourier scatterometry at fixed wavelengths in comparison with our method is lower by the factor of the number of wavelengths used compared with the white light modeling using discrete wavelengths (see the section on ‘Model-based simulation’).
To extract even more information from the measurement data, different extensions may be used. Applying data analysis methods used in classical white light interferometry, which directly take into account the phase information, could also be beneficial.30,31,32,33,34,35 de Groot et al.9 showed that performing a Fourier transform on the white light intensity recorded at every pixel of the pupil plane can yield wavelength-dependent ellipsometric angles for the corresponding incident angle.
The advantage of using a broadband light source is comparable to the advantage of using white light interferometry instead of interferometric measurements at one fixed wavelength. The short coherence length of white light makes it possible to obtain absolute height measurements, because the interference region during a z-scan is confined to a small region when both the optical length of the reference and the object path are matched. Although this absolute height measurement is not possible for subwavelength structures, the sensitivity of the method to the height is still inherent in our method because we use pupil images taken during the reference mirror scan for our analysis.
Conclusion
We have shown the first experimental results for the presented white light interference Fourier scatterometry method. The results support the validity of this method for real-world applications, particularly with regard to the encouraging results obtained in a previous work10 using a simulation-based sensitivity and correlation analysis that was compared with other methods.
The method is well suited for the model-based profile reconstruction of periodic line gratings of silicon, which are often used in the semiconductor industry. The measurements performed were reproduced satisfactorily by simulations. A library search inside the precomputed library identifies the best agreement and gives us the possibility to easily obtain the profile parameters of the analyzed structure.
For even better agreement with the experimentally obtained pupil images, the simulation model should be further extended to include the aberrations of the optical elements used in the experimental setup (illumination path, beam splitter, objectives) and improved calibration routines using standardized samples. Additionally, the effect of line edge roughness on the measured pupil images should be taken into account.
The transfer of this method to other scatterometric metrology applications should be possible without any major inconvenience, as predicted by our simulations shown in a previous publication.10
References
Raymond CJ . Scatterometry for Semiconductor Metrology. In: Diebold AC, editor. Handbook of Silicon Semiconductor Metrology. Boca Raton CRC Press, 2001. pp 477–513.
Raymond CJ . Overview of scatterometry applications in high volume silicon manufacturing. AIP Conf Proc 2005; 788: 394–402.
Silver RM, Barnes BM, Attota R, Jun J, Stocker M et al. Scatterfield microscopy for extending the limits of image-based optical metrology. Appl Opt 2007; 46: 4248–4257.
Boher P . Optical Fourier transform scatterometry for LER and LWR metrology. Proc SPIE 2005; 5752: 192–203.
Osten W, Ferreras Paz V, Frenner K, Schuster T, Bloess H . Simulations of scatterometry down to 22 nm structure sizes and beyond with special emphasis on LER. AIP Conf Proc 2009; 1173: 371–378.
Chen CY, Tsai KY, Shen YT, Lee YM, Li JH et al. Direct-scatterometry-enabled lithography model calibration. Proc SPIE 2012; 8324: 83241R.
Kumar N, El Gawhary O, Roy S, Kutchoukov VG, Pereira SF et al. Coherent Fourier scatterometry: tool for improved sensitivity in semiconductor metrology. Proc SPIE, 2012; 8324: 83240Q.
de Groot PJ, Colonna de Lega X . Transparent film profiling and analysis by interference microscopy. Proc SPIE 2008; 7064: 70640I.
de Groot P, de Lega XC, Liesener J . Model-based white light interference microscopy for metrology of transparent film stacks and optically-unresolved structures. In: Osten W, editor. Proceedings of Fringe 2009: 6th International Workshop on Advanced Optical Metrology. Berlin: Springer; 2009. pp 236–243.
Ferreras Paz V, Peterhansel S, Frenner K, Osten W, Ovsianikov A et al. Depth sensitive Fourier-Scatterometry for the characterization of sub-100 nm periodic structures. Proc SPIE 2011; 8083: 80830M.
Tarantola A . Inverse problem theory and methods for model parameter estimation. Philadelphia Society for Industrial and Applied Mathematics; 2004 .
Groot PD, Lega XCD, Corporation Z, Rd LB . Interpreting interferometric height measurements using the instrument transfer function. Fringe 2005 2005; 2005: 30–37.
ISO/IEC Guide 98:1995—Guide to the expression of uncertainty in measurement (GUM).
Ferreras Paz V, Schuster T, Frenner K, Osten W, Szikszai L et al. Simulation based sensitivity analysis and optimization of scatterometry measurements for future semiconductor technology nodes. Proceedings of Fringe 2009: 6th International Workshop on Advanced Optical Metrology. Berlin: Springer; 2009. pp 592–595.
Osten W, Kerwien N . Resolution enhancement technologies in optical metrology. Proc SPIE 2005; 5776: 10–21.
Silver R, Germer T, Attota R, Barnes BM, Bunday B et al. Fundamental limits of optical critical dimension metrology: a simulation study. Proc SPIE 2007; 6518: 65180U.
Totzeck M, Jacobsen H, Tiziani HJ . Edge localization of subwavelength structures by use of polarization interferometry and extreme-value criteria. Appl Opt 2000; 39: 6295 –6305.
Osten W, Totzeck M . Optics beyond the limits: the future of high precision optical metrology and implications for optical lithography. Proceedings of the ICO 2004, Tokyo, Japan. July 12–15, 2004. pp 589–592.
Totzeck M . Numerical simulation of high-NA quantitative polarization microscopy and corresponding near-fields. Optik 2001; 112: 399–406.
Moharam MG, Grann EB, Pommet DA, Gaylord TK . Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. J Opt Soc Am A 1995; 12: 1068 –1076.
Moharam MG, Pommet DA, Grann EB, Gaylord TK . Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings: enhanced transmittance matrix approach. J Opt Soc Am A 1995; 12: 1077 –1086.
Li L . New formulation of the Fourier modal method for crossed surface-relief gratings. J Opt Soc Am A 1997; 14: 2758 –2767.
Schuster T, Rafler S, Osten W, Reinig P, Hingst T . Scatterometry from crossed grating structures in different configurations. Proc SPIE 2007; 6617: 661715.
Schuster T, Ruoff J, Kerwien N, Rafler S, Osten W . Normal vector method for convergence improvement using the RCWA for crossed gratings. J Opt Soc Am A 2007; 24: 2880 –2890.
Hecht E . Optics. 4th ed. Reading, MA: Addison Wesley Publishing Company; 2001. Vol. 1, p122.
Harder I, Lano M, Lindlein N, Schwider J . Eigenschaften und Grenzen von Homogenisatoren aus Mikrolinsenarrays. DGaO-Proceedings 2004. DGaO Bad Kreuznach.
Raymond CJ . Comparison of solutions to the scatterometry inverse problem. Proc SPIE 2004; 5375: 564–575.
Schuster T, Rafler S, Frenner K, Osten W . Influence of line edge roughness (LER) on angular resolved and on spectroscopic scatterometry. Proc SPIE 2008; 7155: 71550W.
Bilski B, Frenner K, Osten W . About the influence of line edge roughness on measured effective–CD. Opt Express 2011; 19: 19967 –19972.
Takeda M, Ina H, Kobayashi S . Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J Opt Soc Am 1982; 72: 156 –160.
de Groot P, Deck L . Surface Profiling by Analysis of White-light Interferograms in the Spatial Frequency Domain. J Modern Opt 1995; 42: 389–401.
Larkin KG . Efficient nonlinear algorithm for envelope detection in white light interferometry. J Opt Soc Am A 1996; 13: 832 –843.
Sandoz P . Wavelet transform as a processing tool in white-light interferometry. Opt Letters 1997; 22: 1065 –1067.
Recknagel RJ, Notni G . Analysis of white light interferograms using wavelet methods. Opt Commun 1998; 148: 122–128.
Saraç Z, Dursun A, Yerdelen S, Ecevit FN . Wavelet phase evaluation of white light interferograms. Measurement Science and Technology 2005; 16: 1878–1882.
Acknowledgements
We are thankful for the technical support given by Thomas Schoder. This work was supported by the German DFG-funded priority program (SPP1327) on ‘Optically generated sub-100 nm structures for technical and bio-medical applications’ within the subproject ‘Development of a functional sub-100 nm 3D two-photon polymerization technique and optical characterization methods’ and the DFG project ‘Inverse-source and inverse-diffraction problems in photonics (OS111/32-1).’
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
This work is licensed under the Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Ferreras Paz, V., Peterhänsel, S., Frenner, K. et al. Solving the inverse grating problem by white light interference Fourier scatterometry. Light Sci Appl 1, e36 (2012). https://doi.org/10.1038/lsa.2012.36
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2012.36
Keywords
This article is cited by
-
The shape parameters of coal and gangue particles derived from 3D scanning
Scientific Data (2023)
-
“Metrology is a key component of the industrial value-added chain”: an interview with Prof. Wolfgang Osten
Light: Science & Applications (2022)
-
Photonic-dispersion neural networks for inverse scattering problems
Light: Science & Applications (2021)
-
Lensless diffractive imaging with ultra-broadband table-top sources: from infrared to extreme-ultraviolet wavelengths
Light: Science & Applications (2014)