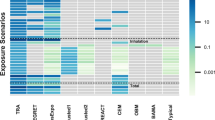
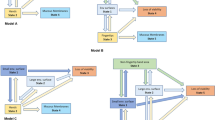
Abstract
Many dermal exposure models use stochastic techniques to sample parameter distributions derived from experimental data to more accurately represent variability and uncertainty. Transfer efficiencies represent the fraction of a surface contaminant transferred from the surface to the skin during a contact event. Although an important parameter for assessing dermal exposure, examination of the literature confirms that no single study is large enough to provide a basis for a transfer efficiency distribution for use in stochastic dermal exposure models. It is therefore necessary to combine data sets from multiple studies to achieve the largest data set possible for distribution analysis. A literature review was conducted to identify publications reporting transfer efficiencies. Data sets were compared using the Kruskal–Wallis test to determine whether they arise from the same distribution. Combined data were evaluated for several theoretical distributions using the Kolmogorov–Smirnov and χ2-goodness-of-fit tests. Our literature review identified 35 studies comprising 25 different sampling methods, 25 chemicals, and 10 surface types. Distributions were developed for three different chemicals (chlorpyrifos, pyrethrin I, and piperonyl butoxide) on three different surface types (carpet, vinyl, and foil). Only the lognormal distribution was consistently accepted for each chemical and surface combination. Fitted distributions were significantly different (Kruskal–Wallis test; P<0.001) across chemicals and surface types. In future studies, increased effort should be placed on developing large studies, which more accurately represent transfer to human skin from surfaces, and on developing a normative transfer efficiency measure so that data from different methodologies can be compared.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 6 print issues and online access
$259.00 per year
only $43.17 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Burmaster D.E., and Crouch E.A.C. Lognormal distributions for body weight as a function of age for males and females in the United States, 1976–1980. Risk Anal 1997: 17 (4): 499–505.
Camann D., Harding H., Geno P., and Agrawl S. Comparison of Methods to Determine Dislodgeable Residue Transfer from Floors (EPA/600/R96/089) United States Environmental Protection Agency, Research Triangle Park, NC, 1996.
Camann D.E., Majumdar T.K., and Harding H.J. Comparison of Salivary Fluids with Respect to Pesticide Transfer Efficiency from carpet to Saliva-Moistened Hands (SWRI Project 01-7131) Southwest Research Institute, San Antonio, TX, 1995.
Canales R.A., and Leckie J.O. Application of a stochastic model to estimate children's short-term residential exposure to lead. Stoch Environ Res Risk Assess 2006: 21: 737–745.
Clothier J. Dermal Transfer Efficiency of Pesticides from New Vinyl Sheet Flooring to Dry and Wetted Palms (EPA/600/R00/029) United States Environmental Protection Agency, Research Triangle Park, NC, 2000.
Cohen Hubal E.A., Sheldon L.S., Burke J.M., McCurdy T.R., Berry M.R., Rigas M.L., Zartarian V.G., and Freeman N.C.G. Children's exposure assessment: a review of factors influencing children's exposure, and the data available to characterize and assess that exposure. Environ Health Perspect 2000: 108 (6): 475–486.
Cohen Hubal E.A., Suggs J.C., Nishioka M.G., and Ivanic W.A. Characterizing residue transfer efficiencies using a fluorescent imaging technique. J Expo Anal Environ Epidemiol 2005: 15: 261–270.
Cullen A.C., and Frey H.C. Probabilistic Techniques in Exposure Assessment. Plenum Press, New York, NY, 1999.
Fenske R.A. Dermal exposure: a decade of real progress. Ann Occup Hyg 2000: 4 (7): 489–491.
Finley B., Proctor D., Scott P., Harrington N., Paustenbach D., and Price P. Recommended distributions for exposure factors frequently used in health risk assessment. Risk Anal 1994: 14: 533–553.
Fortune C. Round-Robin Testing of Methods for Collecting Dislodgeable Residues from Carpets (EPA/600/R97/107) United States Environmental Protection Agency, Research Triangle Park, NC, 1997a.
Fortune C. Evaluation of Methods for Collecting Dislodgeable Pesticide Residues from Turf (EPA/600/R97/119) United States Environmental Protection Agency, Research Triangle Park, NC, 1997b.
Frey H.C., and Cullen A.C. Distribution Development for Probabilistic Exposure Assessment. In: Proceedings of the 88th Annual Meeting of the Air and Waste Management Association, June 18–25, 1995, San Antonio, TX, paper no. 95-TA42.02 1995.
Geno P., Camann D., Harding J., Villalobos K., and Lewis R. Handwipe sampling and analysis procedure for the measurement of dermal contact with pesticides. Arch Environ Contam Toxicol 1996: 30: 132–138.
Hore P., Zartariang V., Xue J., Ozkaynak H., Wang S.W., Yang Y.C., Chu P.L., Sheldon L., Robson M., Needham L., Barr D., Freeman N., Georgopoulos P., and Lioy P.J. Children's residential exposure to chlorpyrifos: application of CPPAES field measurements of chlorpyrfios and TCPy within MENTOR/SHEDS-Pesticides model. Sci Tot Environ 2006: 366 (2–3): 525–537.
Hsu J.P., Camann D.E., Shattenberg H.J., Wheeler H.G., Villalobos K.M., Quarderer S., and Lewis R.G. New Dermal Exposure Sampling Technique. In: Measurement of Toxic and Related Air Pollutants, VIP-17 Air & Waste Management Association, Pittsburgh, PA, 1990, 489–497.
Johnson W., Ferguson A., Hager P., Sandou A., and Shenoda D. Development of a Data Acquisition System for the Measurement of Residue Transfer Coefficient. Presented at ASEE Annual Conference and Exposition: Excellence in Education, Chicago, IL 2006.
Krieger R., Bernard C., Dinoff T., Fell L., Osimitz T., Ross J., and Thongsinthusak T. Biomonitoring and whole body cotton dosimetry to estimate potential human dermal exposure to semi-volatile chemicals. J Expo Anal Environ Epidemiol 2000: 10: 50–57.
Law A.M., and Kelton W.D. Simulation Modeling and Analysis. 3rd edn. McGraw Hill, San Francisco, CA, 2000.
Rice J.A. Mathematical Statistics and Data Analysis, 2nd edn. Duxbury Press, Belmont, CA, 1995.
Ross J., Fong H.R., Thongsinthusak T., Margetich S., and Krieger R. Measuring potential dermal transfer of surface pesticide residue generated from indoor fogger use: using the CDFA roller methods. Chemosphere 1991: 22: 975–984.
Thompson K.M. Developing univariate distributions from data for risk analysis. Hum Ecol Risk Assess 1999: 5 (4): 755–783.
US EPA. Options for Development of Parametric Probability Distributions for Exposure Factors (EPA/600/R-00/058) United States Environmental Protection Agency, Washington, DC, 2000.
Vaccaro J.R., and Cranston R.J. Evaluation of Dislodgeable Residues and Absorbed Doses of Chlorpyrifos Following Indoor Broadcast Applications of Chlorpyrifos-Based Emulsifiable Concentrate Internal Report Dow Chemical, Midland, MI, 1990.
Xue J., Zartarian V., Moya J., Freeman N., Beamer P., Black K., Tulve N., and Shalat S. A meta-analysis of children's hand-to-mouth frequency data for estimating non-dietary ingestion exposure. Risk Anal 2007: 27 (2): 411–420.
Xue J., Zartarian V.G., Ozkaynak H., Dang W., Glen G., Smith L., and Stallings C. A probabilistic arsenic exposure assessment for children who contact CCA-treated playsets and decks, part 2: sensitivity and uncertainty analyses. Risk Anal 2006: 26: 533–541.
Zartarian V.G., Ozkaynak H., Burke J.M., Zufall M.J., Rigas M.L., and Furtaw E.J. A modeling framework for estimating children's residential exposure and dose to chlorpyrifos via dermal residue contact and non-dietary ingestion. Environ Health Perspect 2000: 108: 505–514.
Zartarian V.G., Xue J., Ozkaynak H., Dang W., Glen G., Smith L., and Stallings C. A probabilistic arsenic exposure assessment for children who contact CCA-treated playsets and decks, part 1: model methodology, variability results and model evaluation. Risk Anal 2006: 26: 515–531.
Zartarian V.G., and Leckie J.O. Dermal exposure: the missing link. Environ Sci Technol 1998: 32 (5): 134A–137A.
Acknowledgements
We thank Stanford's Dean Doctoral Diversity Fellowship; Stanford NIH Graduate Training Program in Biotechnology; Harvard School of Public Health's Alonzo Yerby Fellowship; EPA STAR grant (#RA2936201); CHAMACOS, supported by EPA grant #R826709 and NIEHS grant #5P01 ES09605; and the UPS Foundation (#2DDA103) for funding this work. This work has not been subjected to federal peer and policy review, and therefore does not necessarily reflect the views of the funding agencies. No official endorsement should be inferred.
Author information
Authors and Affiliations
Corresponding author
Additional information
Supplementary Information accompanies the paper on the Journal of Exposure Analysis and Environmental Epidemiology website (http://www.nature.com/jes)
Supplementary information
Rights and permissions
About this article
Cite this article
Beamer, P., Canales, R. & Leckie, J. Developing probability distributions for transfer efficiencies for dermal exposure. J Expo Sci Environ Epidemiol 19, 274–283 (2009). https://doi.org/10.1038/jes.2008.16
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/jes.2008.16
Keywords
This article is cited by
-
Model based prediction of age-specific soil and dust ingestion rates for children
Journal of Exposure Science & Environmental Epidemiology (2022)
-
Persistence of indoor permethrin and estimation of dermal and non-dietary exposure
Journal of Exposure Science & Environmental Epidemiology (2020)