Abstract
Successive range expansions occur within all domains of life, where one population expands first (primary expansion) and one or more secondary populations then follow (secondary expansion). In general, genetic drift reduces diversity during range expansion. However, it is not clear whether the same effect applies during successive range expansion, mainly because the secondary population must expand into space occupied by the primary population. Here we used an experimental microbial model system to show that, in contrast to primary range expansion, successive range expansion promotes local population diversity. Because of mechanical constraints imposed by the presence of the primary population, the secondary population forms fractal-like dendritic structures. This divides the advancing secondary population into many small sub-populations and promotes intermixing between the primary and secondary populations. We further developed a mathematical model to simulate the formation of dendritic structures in the secondary population during succession. By introducing mutations in the primary or dendritic secondary populations, we found that mutations are more likely to accumulate in the dendritic secondary populations. Our results thus show that successive range expansion can promote intermixing over the short term and increase genetic diversity over the long term. Our results therefore have potentially important implications for predicting the ecological processes and evolutionary trajectories of microbial communities.
Similar content being viewed by others
Introduction
Range expansion is a universal process that affects the life histories of nearly every microbial community (Tilman and Kareiva, 1997). Range expansion occurs when a population expands into space that was previously unoccupied by that population. Previous theoretical considerations and experiments with synthetic microbial communities demonstrated that range expansion can dramatically reduce intermixing between populations and deteriorate local population diversity (Hallatschek et al., 2007; Excoffier et al., 2009) (Figure 1a). An important feature of these experiments is that they largely investigated scenarios where different microbial populations expand simultaneously into unoccupied space, which occurs when their growth properties are nearly identical. While there are some situations in nature where this may occur, for example, following the retraction of glaciers after an ice-age (Hewitt, 2000), they are often only the first step of a series of changes in ecological communities over time (Connell and Slatyer, 1977). In general, while there are always some populations that expand first (referred to as the primary expansion or primary population), other populations often follow afterwards (referred to as the secondary expansion or secondary population). This process is known as succession and is pervasive in nature (Connell and Slatyer, 1977). For example, after a forest fire, grasses typically expand before trees. A key point is that because the primary population expands first, it changes the environment. The secondary population must therefore expand and establish within a landscape that is already modified by the primary population, which might constrain and affect their potential expansion (Connell and Slatyer, 1977).
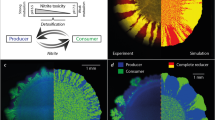
Schematic illustration of (a) simultaneous and (b) successive range expansion (quarter circles of radial expansions). In panel (a), the green and blue colored areas represent two populations that have the same growth properties. In the inoculation zone (lower left) the two populations are well mixed. During expansion, genetic drift at the expansion front causes the two populations to segregate into sectors, which reduces intermixing and local population diversity. The boundaries are parallel to the direction of expansion because the growth properties of the two populations are identical. Panel (b) represents a successive range expansion of a primary population (blue) and a secondary population (green). The successive expansion could cause a segregation of the primary from the secondary population perpendicular to the direction of expansion, which would lead to two successive expansions and an even further reduction in intermixing and local population diversity.
While successive range expansions have primarily been studied for vegetative communities, such as the forest fire example described above, they likely occur for all organisms. For example, there is evidence for two major expansions of humans in the Paleolithic. The first expansion presumably consisted of hunters and gatherers that moved out of Africa. The second expansion consisted of farmers that expanded from the Middle East into areas that were already colonized by the hunters and gatherers (Sokal et al., 1991; Cavalli-Sforza et al., 1993). Succession may also occur among the smallest of organisms: microbes (Fierer et al., 2010). A canonical example of microbial succession is biofilms on teeth that are periodically removed via brushing. After biofilm removal, primary populations attach to the surfaces of cleaned teeth via specialized surface proteins and begin to expand. Secondary populations then attach to those biofilms and expand through the biofilms produced by the primary populations (Rickard et al., 2003; Kolenbrander et al., 2010). Other examples are the colonization and re-colonization (for example, after antibiotic treatment) of the human gut and the colonization and corrosion of water distribution pipes (Fierer et al., 2010).
Although successive expansions are often observed in natural microbial ecosystems, they have not been widely investigated experimentally or theoretically (Fierer et al., 2010). Conceptually, succession can be seen as two temporally segregated expansions of microorganisms (Figure 1b), which implies a complete segregation of the two populations in the direction of the expansion. The consequence is a reduction of intermixing of the two populations, and thus a reduction of local population diversity, which may have important consequences on microbial processes.
The objective of this study was to quantitatively assess how successive expansion affects local population diversity (intermixing) between primary and secondary populations. We expect that successive expansion will reduce intermixing between populations and, consequently, reduce local population diversity relative to simultaneous expansion (Figure 1). To address this objective, we constructed an experimental system that allowed us to impose a metabolic interaction that promotes successive expansion of two populations of the bacterium Pseudomonas stutzeri A1501 growing on agar plates. P.stutzeri is a gram-negative, rod-shaped (1–3 m long and about 0.5 m wide) bacterium that typically has a single flagellum located at a pole and type IV pili that enable twitching motility (Lalucat et al., 2006). Twitching motility is a mode of movement of bacteria on soft and wet surfaces such as semi-solid agar (Henrichsen, 1972). However, on standard hard agar plates, which were used in the experiments described here, bacteria are typically considered non-motile (Ben-Jacob et al., 2000; Hallatschek et al., 2007).
Important for our study, P. stutzeri is a facultative anaerobe that can use nitrate as an electron acceptor in the absence of oxygen in a process called denitrification (Lalucat et al., 2006). P. stutzeri can perform the complete denitrification pathway (referred to as the complete degrader) in which nitrate is sequentially reduced to nitrite, nitric oxide, nitrous oxide, and finally to dinitrogen gas (Zumft, 1997). We previously deleted specific genes within the P. stutzeri A1501 genome to construct two isogenic mutant strains that cross-feed the metabolic intermediate nitrite (Lilja and Johnson, 2016). One strain partially metabolizes nitrate to nitrite (referred to as the producer) while the other strain metabolizes nitrite to dinitrogen gas (referred to as the consumer).
Because the consumer cannot grow before the producer when nitrate is provided as the growth-limiting substrate, we expected the cross-feeding populations to undergo successive range expansion when grown together in the absence of oxygen, where the producer expands first and the consumer follows. Each strain carries a gene encoding for a different fluorescent protein, thus allowing us to quantify the resulting spatial patterns and the magnitude of intermixing between populations. We then compared the results for co-cultures of the producer and consumer (that is, two strains that cross-feed nitrite and presumably expand sequentially) with the results for co-cultures of two complete degraders (that is, two ancestral strains that completely reduce nitrate to dinitrogen gas, have the same growth properties and therefore expand simultaneously). In addition, we developed a two-dimensional reaction–diffusion model that allowed us to predict the long-term effects of successive range expansion on local genetic diversity within the primary or secondary expansion.
Materials and methods
Bacterial strains and growth conditions
We used a previously developed experimental microbial system for all our experiments, which is described in detail elsewhere (Lilja and Johnson, 2016; Lilja and Johnson, 2017) (see Supplementary Table 1). Briefly, the narG or nirS gene was deleted from P. stutzeri A1501. The producer contains a deletion in nirS, which encodes for an enzyme essential for the reduction of nitrite to nitrous oxide and therefore reduces nitrate to nitrite but does not reduce nitrite (Zumft, 1997). The consumer contains a deletion in narG, which encodes for an enzyme essential for the reduction of nitrate to nitrite and therefore reduces nitrite to dinitrogen gas but does not reduce nitrate (Zumft, 1997). Both strains further contain a deletion in comA, which is a transporter required for competence. Deletion of this gene reduces the probability of recombination during experimentation (Lilja and Johnson, 2016). To enable fluorescence microscopy, we introduced different fluorescent protein-encoding genes (green- or cyan-fluorescent protein-encoding genes) into the strains as described in the Supplementary Information and elsewhere (Lilja and Johnson, 2017). The strains, plasmids and primers used to construct all the strains are provided in Supplementary Tables 1 and 2.
Anaerobic colony expansion assay
We implemented a modified anaerobic version of the expansion experiment described by Hallatscheck et al. (2007). We first grew different strains of P. stutzeri separately overnight in LB medium under aerobic conditions. We then adjusted the cell densities of the cultures (see the Supplementary Information for details), mixed the cultures according to experimental needs as described in the results section (for example, the producer and consumer at a ratio of 1:1 (cell number:cell number)) and transferred the cultures to an anaerobic glove box. We then deposited 2-μl drops of the cell mixtures onto the centers of anaerobic agar plates (one drop per plate), allowed the drops to dry for 1 h and incubated the plates at 21 °C for up to 4 weeks. We finally exposed the plates for 1 h to ambient air to induce maturation of the fluorescent proteins and imaged the colonies with a confocal microscope (Leica TCS SP5 II). We performed image analysis in FIJI and data analysis in R (www.r-project.org) (complete descriptions are available in the Supplementary Information).
Intermixing index
We defined intermixing similar to the definitions described previously (Pielou, 1966; Momeni et al., 2013). Briefly, we divided the measured number of intersections between different populations at a given radius (Nr) by the expected number of intersections for a random spatial distribution of two populations (E(Nr)) (a complete description is available in the Supplementary Information). The normalization to E(Nr) accounts for the expected increase of intersections due to the inflation of the radius during expansion and contrasts the observed pattern to a completely mixed and random spatial distribution. We thus defined intermixing at a given radius (Ir) as:

Modeling
We developed a spatially explicit reaction–diffusion model to simulate successive expansion of two populations that exchange a metabolic intermediate. The model consists of a producer (P), a consumer (C), and two substrates nitrate (N1) and nitrite (N2), each of which is modeled on a separate square lattice of size 1024 × 1024. Initially, only substrate N1 is present while substrate N2 is produced by P. At the beginning of the simulations, P and C are randomly deposited on a circular area in the middle of the grid. They are subsequently allowed to grow and expand over time. To efficiently model the two populations and two substrates on large spatial grids, a part of the code was parallelized using GPU acceleration as described elsewhere (van de Koppel et al., 2011). The model is written in CUDA, which allows the execution of parts of the code on a graphics processor. We analyzed and visualized the model output in Matlab (MathWorks, Natick, MA, USA).
The equations for the bacteria consist of a diffusion term and a growth term. The diffusion terms for the producer and consumer are not constant, but instead depend on the local concentrations of the substrates, the densities of the two strains, and a local anisotropy term Ω. Diffusion of the cells is only possible as long as the respective substrate is present. Moreover, diffusion is facilitated by the focal local population density (Mimura et al., 2000) and hindered by the local population density of the other population (note how P and C are interchanged in equations (2b) and (3b)). The anisotropy term Ω is a locally varying random number with a value of either 0 or 100 that is assigned to each grid cell. The values and distribution of Ω can be used to change the properties of the dendritic pattern. σ is a scaling factor to balance the expansion speeds of the two populations. Growth is modeled with a Monod-type term with a maximal growth rate (r) and a substrate specific half-velocity constant (K).




The equations of the two substrates consist of a constant diffusion term (with diffusion constants DN1 and DN2), a consumption term that is proportional to the growth of the respective bacterial populations (ν) and a production term for N2 that is equal to the consumption of N1, reflecting the 1:1 stoichiometric relationship of the production of nitrite from nitrate.


We used generic parameters for all simulations (parameters are provided in Supplementary Table 3).
Results
Dendrite formation increases intermixing
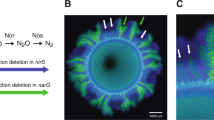
We grew co-cultures of two complete degraders (simultaneous expansion) or co-cultures of the producer and the consumer (successive expansion) on anaerobic agar plates supplied with nitrate as the growth-limiting substrate. The complete degraders formed sectors with saw-tooth like boundaries between the two populations. These boundaries were oriented parallel to the axis of expansion, similar to the patterns described previously for the expansion of metabolically identical populations of Escherichia coli (Hallatschek et al., 2007) (Figure 2a). In contrast, the producer and consumer expanded successively; the producer expanded first while the consumer followed (Figure 2b). The producer completely covered the expansion area and had a relatively continuous expansion front similar to that observed for the complete degraders. In contrast, the consumer unexpectedly formed branched dendrites that extended into the space occupied by the producer (Figure 2b). Each dendrite typically originated at a single point from the inoculation zone (referred to as a stem) and branched during expansion (referred to as the formation of tips). The tips were directly connected to a single stem and had clear boundaries with the producer. The dendrites typically did not touch each other, but were instead separated by a thin layer of the producer (see Supplementary Figure 1 for a detailed Z-stack of the dendrites). The number of dendrites decreased with the direction of the expansion, qualitatively similar to the decrease in the number of sectors between completely degrading strains (Hallatschek et al., 2007).
Expansion of co-cultures of complete degraders or co-cultures of the producer and consumer and quantification of intermixing. (a1+2) For co-cultures of complete degraders, sectors with boundaries lying parallel to the axis of expansion emerged. (b1+2) For co-cultures of producers and consumers, two successive expansions emerged, where the producer (blue) formed a continuous non-dendritic expansion while the consumer (green) formed a dendritic expansion. The seven larger dendrites that can be seen in b1 could potentially be genetic mutants, but further experiments are needed to test this hypothesis. (c) Measurement of intermixing between the producer and the consumer from the center of colonies towards the edge of expansion Left) Intermixing index at radial position, the blue line is a locally weighted scatterplot smoother (loess), the red lines indicate the beginning and end of the secondary expansion by the consumer (see the Supplementary Information). Intermixing is relatively constant in the inoculation zone, then increases and peaks in the expansion zone. Right) Intermixing in the secondary expansion is significantly higher than in the inoculum (Mann–Whitney test, P < 2.2e-16).
The dendritic nature of the secondary expansion promoted increased intermixing of the two populations, which was opposite to our initial expectation (Figure 1). To quantify this, we defined an intermixing index similar to previous studies (Pielou, 1966; Momeni et al., 2013) as the number of transitions between the consumer and producer divided by the expected number of transitions from a random distribution at a certain circumference (see the Supplementary Information for a complete description). An intermixing index larger than one indicates more mixing than a completely mixed random distribution while an intermixing index smaller than one indicates more segregation than a completely mixed random distribution. Note that in natural systems the latter is the predominant case (Pielou, 1966). We found that intermixing was relatively constant in the inoculation zone (mean=0.1609, s.e.=0.0004), but increased and then remained relatively constant in the secondary expansion (mean=0.1743, s.e.=0.0005) (Figure 2c). Overall, intermixing increased by 8.35% during secondary expansion (Mann–Whitney test, P < 2.2e-16). The reason for this increase is that growth during early stages of colony development led to clumping in the inoculation zone. This clumping was more pronounced and can be seen clearly in Figures 3a. Our results thus show that branching of the secondary expansion promoted intermixing during the early development of the dendrites and then produced a dendritic pattern which maintained intermixing thereafter (Figure 2c). This increase and maintenance of diversity is fundamentally different from the demixing effect of drift during primary expansion, which generally leads to a decrease of diversity during expansion (Hallatschek et al., 2007; Mitri et al., 2016).
Microscopy images of range expansions with different growth limiting factors that were devised to assess the causes of dendrite formation. (a1+2) Co-cultures of the producer (blue) and consumer (green) grown together with exogenous supplies of both nitrate and nitrite. The area outside of the colony was colored white to visualize the expansion edge (a2 magnification). The strains still succeeded each other and the consumer formed dendrites even though nitrite was added exogenously. (b) Co-cultures of the consumer grown alone (in green and red) on plates containing nitrite, which did not form dendrites. (c) The producer (blue) expanding into space previously occupied by the consumer (green) on plates containing exogenous supplies of both nitrate and nitrite, where the producer formed dendrites.
Mechanical constraints likely caused dendrite formation
To infer the mechanism of branching during succession, we analyzed the structure of the dendritic pattern in more detail. The dendrites formed by the consumer qualitatively resemble the fractal branching-type patterns generated by the diffusion-limited aggregation (DLA) process. Diffusion-limited aggregation is a computer model to generate dendritic patterns that have fractal properties, meaning that the dendritic pattern repeats itself over several orders of magnitude of observation. Since its discovery, DLA has received increasing attention because similar patterns have been repeatedly observed in diverse natural systems, including bacterial growth on agar plates (Fujikawa and Matsushita, 1989). The fractal properties are quantified by the fractal dimension (FD), which can be measured using image analysis. We found that the FD of the consumer dendrites (mean FD=1.73, standard deviation (s.d.)=0.03, N=8) is comparable to the FD of the DLA process (FD≅1.71) (May and Maher, 1989).
The mechanisms causing the formation of DLA-type dendrites in bacteria have typically been attributed to diffusion limitation of the growth substrate and/or to mechanical constraints, both of which can cause instabilities at the advancing front that lead to dendrite formation (Ben-Jacob et al., 1994; Mimura et al., 2000). Examples of mechanical constraints are movement over hard agar surfaces (Ben-Jacob et al., 1994; Mimura et al., 2000) or movement in the presence of other cells (Mather et al., 2010; Rudge et al., 2013). Our observed similarity of pattern formation during expansion of the consumer with DLA-like fractals thus suggests that one or both of these two mechanisms could have caused the formation of the observed dendrites. The first is that the expansion of the consumer is constrained by the availability of the growth-limiting cross-fed substrate (Ben-Jacob et al., 1994; Mimura et al., 2000) while the second is that the expansion of the consumer is mechanically constrained by the presence of the producer biofilm, and consumer cells must therefore advance via mechanical cell shoving through the producer (Mather et al., 2010; Rudge et al., 2013). Both mechanisms can produce patterns with the same FD as DLA and can therefore not be distinguished by simple observation of the pattern (Mathiesen et al., 2006). We therefore designed experiments to qualitatively analyze the relative contributions of the two mechanisms to dendrite formation during the expansion of the consumer.
To test whether substrate limitation caused the formation of dendrites, we grew co-cultures of the producer and consumer on agar plates containing exogenous and excess supplies of both nitrate and nitrite, thus reducing the possibility that the limited amount of nitrite produced via cross-feeding caused the dendrite formation during expansion of the consumer. We found that, even when both nitrate and nitrite were provided exogenously, the two populations continued to form two successive expansions, where the consumer expanded after the producer. More importantly, even though the consumer had greater availability of its growth-limiting substrate nitrite than the producer (note that nitrite was provided exogenously and produced via the activity of the producer), it nevertheless still produced dendritic patterns during expansion that were similar to those observed when only nitrate was provided exogenously (Figure 3a, FD: mean 1.691, s.d.=0.007, Intermixing index: mean 0.216, s.e.=0.002). The reason for this observation is likely due to small differences in the lag time before cells begin consuming nitrate or nitrite. Cells immediately consume nitrate but undergo a small lag before beginning to consume nitrite (Supplementary Figure 2). This small difference in lag times then result in successive expansion, even when nitrate and nitrite are supplied simultaneously to the medium.
To further exclude the possibility that the consumer was limited by the availability of nitrite, we increased the nitrate concentration up to 10 mM (which is an order of magnitude higher than in the previous experiments). We still observed successive growth dynamics with dendrite formation of the consumer under these conditions. However, the producer expanded more extensively at the higher nitrate concentration (about 35%, see Supplementary Figure 3), that is, the producer profited disproportionally. This was presumably because the greater biomass of the producer further inhibited the advancement of the consumer due to stronger mechanical constraints. Furthermore, we grew two differently labeled consumers (that is, they produced either green or red fluorescent protein) together on agar plates containing nitrite as the only available electron acceptor. The consumers did not form dendrites when growing in the absence of the producer. Similar to the completely degrading strains, the consumers formed sectors with boundaries that lied approximately parallel to the direction of expansion (Figure 3b). Together, these results indicate that substrate availability was likely not the main growth-limiting factor, and therefore likely not the main cause of dendrite formation.
This leaves the hypothesis that dendrite formation during expansion of the consumer was mainly caused by mechanical constraints imposed on the consumer by having to expand into space previously occupied by the producer. If this were a potentially general mechanism, one would expect that different strains that grow into previously occupied space produce similar patterning (Mather et al., 2010). To test this hypothesis, we devised an experiment where the producer had to expand into space occupied by the consumer (note that this is the reverse of the expansion ordering imposed previously). To accomplish this, we inoculated the producer at low frequencies (below 100 cells per colony) on plates containing exogenous supplies of both nitrate and nitrite. The producer population thus consisted of isolated cells that were embedded within the consumer biofilm and had to grow through the consumer to expand. We found that the producer also formed dendrites when expanding into space occupied by the consumer (Figure 3c). Taken together, while our data cannot conclusively rule out nitrite limitation as an important factor in dendrite formation, all of our data points towards nitrite limitation not being the main driver of dendrite formation. The collective outcomes of these experimental results instead indicate that mechanical constraints were likely a more important driver causing dendrite formation in the secondary expansion.
Mutants establish more readily in the secondary expansion
The fundamentally different shape of the dendritic secondary expansion raises the question of whether the different shapes of the non-dendritic primary and dendritic secondary expansions cause differences in the long-term molecular evolution of the populations. The idea here is that a mutant that occurs during expansion has to compete with the surrounding actively growing ancestral population for space and/or nutrients. The larger this active population is, the harder it is for a mutant to establish and increase in frequency (Excoffier et al., 2009). In the continuous non-dendritic primary expansion, the active population is relatively large, making it more difficult for the mutant to establish. In contrast, in the dendritic secondary expansion, the active population at the tip of an expanding dendrite is very small, making it easier for a mutant to establish and increase in frequency (Excoffier and Ray, 2008). The long-term effect would therefore be a higher accumulation of mutations in a dendritic secondary expansion than in a non-dendritic primary expansion.
We developed a mathematical model that allowed us to reproduce key features of the experimental data and study the dynamics of successive range expansions and the branching of the dendritic secondary expansion on molecular evolution. Building on earlier approaches of modeling dendritic expansion of single microbial species on agar plates (Kawasaki et al., 1997; Golding et al., 1998; Mimura et al., 2000), we selected a reaction–diffusion model with non-linear diffusion terms for the microbial populations. In these models, microbial diffusion (that is, microbial movement) is dependent on substrate concentrations and local population sizes. We extended this approach by including a dependency on a second microbial population in order to represent our model system and experimental findings.
The model consists of lattices for the two populations (producer and consumer) and the two corresponding growth-limiting substrates (nitrate and nitrite). The non-linear diffusion terms for microbial movement depend on the concentration of the corresponding limiting nutrient, the concentration of the focal population, the concentration of the other population and a term for local anisotropy (that is, directional dependency) of the biofilm. The rationales for these terms are the following: The dependence on the limiting nutrient ensures that cells only move at the growing edge of the colony, where substrate is available (Mimura et al., 2000). The expansion of each population is slowed by the presence of the other population and accelerated when the density of its own population is high (that is, they can push harder together) (Kawasaki et al., 1997). This form was chosen to reflect our experimental findings suggesting that mechanical constraints are the main drivers of dendrite formation of the secondary expansion, irrespective of whether it consists of the consumer or the producer. The anisotropy term represents the local alignment of packs of rod-shaped cells in bacterial biofilms (Volfson et al., 2008), but anisotropy can be found in other systems as well (Nittmann and Stanley, 1986). The idea here is that if cells from the secondary expansion encounter a pack of rod-shaped cells aligned perpendicular to the direction of expansion, it is more difficult to push through and movement is locally inhibited. On the other hand, if they encounter a pack of cells aligned parallel to the direction of expansion, it is easier to push through and movement is locally facilitated.
The model could qualitatively reproduce the dynamics of the two expansions and the formation of dendrites as was observed experimentally. The two populations underwent successive range expansion and the secondary expansion of the consumer formed dendrites with a FD of 1.798 (s.d.=0.002) (Figure 4b). If two complete consumers were inoculated together, they rapidly formed sectors as was observed experimentally (Figure 4a). While the model captured the pattern dynamics during the expansion, it overestimated intermixing in the inoculation zone and could therefore not capture the increase in intermixing immediately after expansion began. Because we were mainly interested in the dynamics during expansion and in order to keep the model relatively simple, we did not try to simulate this aspect of the experimental observations. The model did, however, capture the maintenance of intermixing due to dendrite formation during the secondary expansion.
Modeling results and predictions. (a) Two completely degrading populations rapidly segregated into sectors. (b) The secondary expansion of the consumer produced fractal dendrites (magnifications of sections of the modeled circular colonies are shown). In the second row the model output with mutants that have a 1.4 times higher maximum growth rate than the ancestor. Blue is the primary and green the secondary population. In panel (c), the red areas indicate mutants in the primary population. It can be seen that they form patches that go extinct relatively rapidly. In panel (d), the mutants (also red) are introduced in the secondary population. In contrast to the mutants in the primary population in panel (c), they can take over dendrites and establish locally. (e) Measurement of the proportion of the mutant in the actively growing part of the population at the end of a simulation at different relative growth advantages. Blue is the non-dendritic primary expansion of the producer and green is the dendritic secondary expansion of the consumer. The data points represent independent simulations. The curves show the Gompertz-model fits and the vertical lines represent the lag-parameter of these models with 95% confidence intervals in grey.
Note that our goal was not to exactly reproduce the patterns found in the experiments, but rather to develop a model that enabled investigating how mutations may establish in non-dendritic primary or dendritic secondary expansions. In fact, the shape of the dendrites is largely dependent on the anisotropy term. By choosing different parameters or a different random distribution, the dendrites become more or less branched. If the anisotropy term is omitted, the pattern becomes a more regular fingering pattern without side branches (see Kawasaki et al. (1997) for a more detailed analysis of the influence of anisotropy on dendrite formation in non-linear diffusion models of microbes and Nittmann and Stanley (1986) for a more general discussion of the role of anisotropy in dendrite formation). Adapting the anisotropy term thus potentially allows one to tune the dendritic structure of the secondary expansion to represent other systems that undergo successive range expansion.
We next introduced mutations into our mathematical model to compare the possible evolutionary differences between non-dendritic primary and dendritic secondary expansions. At every time-step, the entire population of an active lattice site (that is, a population that had substrate available for growth) could mutate with a certain probability from the ancestral population to a new mutant population. The new population could then grow and expand as the ancestral population. We introduced mutations in both the non-dendritic primary and the dendritic secondary expansions. We found that mutant populations rapidly went extinct if the growth rates were exactly the same as the ancestral population.
We thus introduced higher maximal growth rates for the mutants. As the maximal growth rate increased, we found that small patches of mutants first emerged and, if the maximal growth rate was sufficiently higher than that for the ancestral population, the patches could increase in size. The mutants in the non-dendritic primary expansion typically formed patches (Figure 4c) that did not persist for prolonged periods of time unless they had a 50% higher maximal growth rate than the ancestor, at which they rapidly displaced the ancestral population. The mutants in the dendritic secondary expansion, however, could establish dendrites (Figure 4d) that did not disappear throughout the simulations already at 20% higher maximal growth rates. On the other hand it was more difficult for mutants within dendrites to displace the entire resident population because narrow dendrites of the ancestral population could persist even when they had a large growth disadvantage (see also Supplementary Figure 4).
To quantify the difference between dendritic and non-dendritic expansion, we measured the fraction of mutants in the actively growing populations at the end of the simulations for different maximal growth rates. The above-mentioned dynamics are reflected in the shape of the Gompertz curves that were fit to the model data (Figure 4e): the lag-parameter (indicated as vertical shaded lines) and the maximum slope of the dendritic secondary population were significantly smaller for the non-dendritic primary population than for the dendritic secondary population (F-test, both P < 2.2e-16) while the maximum proportion was not (F-test, P=0.379). The consequence is that at the point where the proportion of the mutant in the non-dendritic primary expansion started to increase substantially (that is, at the end of the ‘lag-phase’ and with a growth advantage of about 40% compared to the ancestor), the proportion of the mutants in the dendritic secondary expansion already accounted for about half of the active population. This thus supported our hypothesis that mutants establish more readily in the dendritic secondary expansion than in the non-dendritic primary expansion.
To further test whether this effect was a consequence of our two-strain model, we ran simulations with a single strain model that leads to dendritic expansion. In this model, the inhibition by the secondary strain is omitted, which makes it therefore very similar to previous models of dendritic bacterial growth (Kawasaki et al., 1997). Mutants were also able to establish in branches already at maximal growth rates 10% higher than the ancestors (see Supplementary Figure 5). In the primary expansion, the local concentration of the consumer at the expansion front is zero and the diffusion term therefore simplifies to a form without inhibition. Thus, the results of the primary expansion of the two strain model are the same as for a single strain model without branching. This result indicates that the easier establishment of mutations in dendritic expansion compared to non-dendritic expansions is not just limited to successions, but could potentially be a general phenomenon for any system where dendrite formation occurs.
Discussion
We found that, opposite to our initial expectations (Figure 1), successive range expansion promotes intermixing rather than decreases intermixing in our microbial model system. The cause for this is the formation of dendritic patterns by the secondary expansion. The branching of the secondary expansion thus creates new local population diversity during expansion by splitting up advancing local populations into smaller branches. In our case, the branching resulted in higher intermixing than was even observed in the inoculation zone. Increased intermixing signifies higher spatial heterogeneity, shorter average distances between the two populations and increased interface size. This could affect how the two populations interact with each other, for example, it could facilitate the exchange of biological products (Kolenbrander et al., 2010). Furthermore, it could facilitate genetic exchange between strains, for example, the probability of horizontal gene transfer is proportional to the number of cell–cell contacts (Sørensen et al., 2005; Niehus et al., 2015).
Over longer time-scales, more genetic diversity might establish in the dendritic secondary expansion than in the non-dendritic primary expansion. Our modeling results show that mutations with small growth advantages establish more readily during dendritic expansion. The reason for this is likely the small local population sizes at the tips of dendrites, which makes it easier for a mutant to establish locally. Because mutations that confer small fitness advantages are likely more common than mutations that confer large fitness advantages (Elena and Lenski, 2003), we expect that more mutations will accumulate in the secondary dendritic expansions. The branching of the secondary dendritic expansion can therefore mitigate the loss of diversity due to two mechanisms: promotion of intermixing between the secondary and primary populations and higher accumulation of novel mutations in the secondary population during extended periods of expansion.
An important driver of the branching process is the reduced availability of space to the secondary population, which must expand into areas already colonized by the primary population. While we identified space as an important limiting resource when expanding into a previously colonized area, nutrient limitation might nevertheless also play a role. The similarity to DLA patterns and the importance of mechanical constraints for branching of the secondary expansion suggests that branching could potentially be a general process that affects many populations with limited dispersal capabilities. One example could be tumors that penetrate into the surrounding tissue (Anderson and Quaranta, 2008), where the healthy tissue represents the already colonized area (that is, the primary expansion) and the tumor represents the secondary expansion. Since tumors have high mutation rates and can form dendritic patterns (Ferreira et al., 2002, Anderson and Quaranta, 2008), the accumulation of mutations may play an important role in this case. Another example could be vegetative plants, which usually grow in clustered groups (Dale, 1999). A secondary expansion could thus resemble percolation clusters, which also consist of many small localized regions and exhibit fractal properties. Finally, these processes could potentially also be important for our own species. A recent analysis of the Native American population structure suggests that there were three successive immigration events into the Americas and that there was extensive admixture between the first and the following populations (Reich et al., 2012). In all of these cases, the branched pattern of the secondary expansion does not have to be exactly the same that we observed in this study. The important point is that secondary expansion leads to splitting of the expansion front into small local sub-populations, which maintains intermixing with the primary expansion and may lead to increased accumulation of mutations in the secondary expansion.
References
Anderson AR, Quaranta V . (2008). Integrative mathematical oncology. Nat Rev Cancer 8: 227–234.
Ben-Jacob E, Schochet O, Tenenbaum A, Cohen I, Czirók A, Vicsek T . (1994). Generic modelling of cooperative growth patterns in bacterial colonies. Nature 368: 46–49.
Ben-Jacob E, Cohen I, Levine H . (2000). Cooperative self-organization of microorganisms. Adv Phys 49: 37–41.
Cavalli-Sforza LL, Menozzi P, Piazza A . (1993). Demic expansions and human evolution. Science 259: 639–646.
Connell JH, Slatyer RO . (1977). Mechanisms of succession in natural communities and their role in community stability and organization. Am Nat 111: 1119–1144.
Dale MRT . (1999) Spatial Pattern Analysis in Plant Ecology. Cambridge University Press: Cambridge, UK.
Elena SF, Lenski RE . (2003). Evolution experiments with microorganisms: the dynamics and genetic bases of adaptation. Nat Rev Genet 4: 457–469.
Excoffier L, Foll M, Petit RJ . (2009). Genetic consequences of range expansions. Annu Rev Ecol Evol Syst 40: 481–501.
Excoffier L, Ray N . (2008). Surfing during population expansions promotes genetic revolutions and structuration. Trends Ecol Evol 23: 347–351.
Ferreira SC, Martins ML, Vilela MJ . (2002). Reaction–diffusion model for the growth of avascular tumor. Phys Rev E 65: 21907.
Fierer N, Nemergut D, Knight R, Craine JM . (2010). Changes through time: integrating microorganisms into the study of succession. Res Microbiol 161: 635–642.
Fujikawa H, Matsushita M . (1989). Fractal growth of Bacillus subtilis on agar plates. J Phys Soc Japan 58: 3875–3878.
Golding I, Kozlovsky Y, Cohen I, Ben-Jacob E . (1998). Studies of bacterial branching growth using reaction–diffusion models for colonial development. Phys A 260: 510–554.
Hallatschek O, Hersen P, Ramanathan S, Nelson DR . (2007). Genetic drift at expanding frontiers promotes gene segregation. Proc Natl Acad Sci USA 104: 19926–19930.
Henrichsen J . (1972). Bacterial surface translocation: a survey and a classification. Bacteriol Rev 36: 478–503.
Hewitt G . (2000). The genetic legacy of the Quaternary ice ages. Nature 405: 907–913.
Kawasaki K, Mochizuki A, Matsushita M, Umeda T, Shigesada N . (1997). Modeling spatio-temporal patterns generated by Bacillus subtilis. J Theor Biol 188: 177–185.
Kolenbrander PE, Palmer RJ, Periasamy S, Jakubovics NS . (2010). Oral multispecies biofilm development and the key role of cell–cell distance. Nat Rev Microbiol 8: 471–480.
Lalucat J, Bennasar A, Bosch R, García-Valdés E, Palleroni NJ . (2006). Biology of Pseudomonas stutzeri. Microbiol Mol Biol Rev 70: 510–547.
Lilja EE, Johnson DR . (2016). Segregating metabolic processes into different microbial cells accelerates the consumption of inhibitory substrates. ISME J 10: 1568–1578.
Lilja EE, Johnson DR . (2017). Metabolite toxicity determines the pace of molecular evolution within microbial populations. BMC Evol Biol 17: 52.
Mather W, Mondragón-Palomino O, Danino T, Hasty J, Tsimring LS . (2010). Streaming instability in growing cell populations. Phys Rev Lett 104: 208101.
Mathiesen J, Procaccia I, Swinney HL, Thrasher M . (2006). The universality class of diffusion-limited aggregation and viscous fingering. Europhys Lett 76: 257–263.
May SE, Maher JV . (1989). Fractal dimension of radial fingering patterns. Phys Rev A 40: 1723–1726.
Mimura M, Sakaguchi H, Matsushita M . (2000). Reaction–diffusion modelling of bacterial colony patterns. Phys A 282: 283–303.
Mitri S, Clarke E, Foster KR . (2016). Resource limitation drives spatial organization in microbial groups. ISME J 10: 1471–1482.
Momeni B, Brileya KA, Fields MW, Shou W . (2013). Strong inter-population cooperation leads to partner intermixing in microbial communities. Elife 2: e00230.
Niehus R, Mitri S, Fletcher AG, Foster KR . (2015). Migration and horizontal gene transfer divide microbial genomes into multiple niches. Nature Commun 6: 8924.
Nittmann J, Stanley HE . (1986). Tip splitting without interfacial tension and dendritic growth patterns arising from molecular anisotropy. Nature 321: 663–668.
Pielou EC . (1966). Species-diversity and pattern-diversity in the study of ecological succession. J Theor Biol 10: 370–383.
Reich D, Patterson N, Campbell D, Tandon A, Mazieres S, Ray N et al. (2012). Reconstructing Native American population history. Nature 488: 370–374.
Rickard AH, Gilbert P, High NJ, Kolenbrander PE, Handley PS . (2003). Bacterial coaggregation: an integral process in the development of multi-species biofilms. Trends Microbiol 11: 94–100.
Rudge T, Federici F, Steiner PJ, Haseloff J . (2013). Cell polarity-driven instability generates self-organized, fractal patterning of cell layers. ACS Synthetic Biol 2: 705–714.
Sokal RR, Oden NL, Wilson C . (1991). Genetic evidence for the spread of agriculture in Europe by demic diffusion. Nature 351: 143–145.
Sørensen SJ, Bailey M, Hansen LH, Kroer N, Wuertz S . (2005). Studying plasmid horizontal transfer in situ: a critical review. Nat Rev Microbiol 3: 700–710.
Tilman D, Kareiva PM . (1997) Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interactions. Princeton University Press: Princeton, NJ.
van de Koppel J, Gupta R, Vuik C . (2011). Scaling-up spatially-explicit ecological models using graphics processors. Ecol Modell 222: 3011–3019.
Volfson D, Cookson S, Hasty J, Tsimring LS . (2008). Biomechanical ordering of dense cell populations. Proc Natl Acad Sci USA 105: 15346–15351.
Zumft WG . (1997). Cell biology and molecular basis of denitrification. Microbiol Mol Biol Rev 61: 533–616.
Acknowledgements
We thank Fordyce A. Davidson for valuable insights and suggestions on how to design the non-linear diffusion term of the microbial populations in the model; Lara Pfister, Selina Derksen-Müller and Anja Bernet for help with the strain construction; Lea Caduff for help with the microscopy; and Martin Ackermann and Will Macnair for helpful discussions and comments on early versions of the manuscript. We also thank two anonymous reviewers for significantly improving the quality and clarity of this manuscript. This work was supported by grants from the Swiss National Science Foundation (31003A_149304) and SystemsX.ch, The Swiss Initiative in Systems Biology (MicroScapesX.ch).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on The ISME Journal website
Supplementary information
Rights and permissions
About this article
Cite this article
Goldschmidt, F., Regoes, R. & Johnson, D. Successive range expansion promotes diversity and accelerates evolution in spatially structured microbial populations. ISME J 11, 2112–2123 (2017). https://doi.org/10.1038/ismej.2017.76
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/ismej.2017.76
This article is cited by
-
Phage predation accelerates the spread of plasmid-encoded antibiotic resistance
Nature Communications (2024)
-
Evaporation-induced hydrodynamics control plasmid transfer during surface-associated microbial growth
npj Biofilms and Microbiomes (2023)
-
Timing of antibiotic administration determines the spread of plasmid-encoded antibiotic resistance during microbial range expansion
Nature Communications (2023)
-
Rare and localized events stabilize microbial community composition and patterns of spatial self-organization in a fluctuating environment
The ISME Journal (2022)
-
Initial community composition determines the long-term dynamics of a microbial cross-feeding interaction by modulating niche availability
ISME Communications (2022)