Abstract
As sequencing technologies have advanced, the amount of information regarding the composition of bacterial communities from various environments (for example, skin or soil) has grown exponentially. To date, most work has focused on cataloging taxa present in samples and determining whether the distribution of taxa shifts with exogenous covariates. However, important questions regarding how taxa interact with each other and their environment remain open thus preventing in-depth ecological understanding of microbiomes. Time-series data from 16S rDNA amplicon sequencing are becoming more common within microbial ecology, but methods to infer ecological interactions from these longitudinal data are limited. We address this gap by presenting a method of analysis using Poisson regression fit with an elastic-net penalty that (1) takes advantage of the fact that the data are time series; (2) constrains estimates to allow for the possibility of many more interactions than data; and (3) is scalable enough to handle data consisting of thousands of taxa. We test the method on gut microbiome data from white-throated woodrats (Neotoma albigula) that were fed varying amounts of the plant secondary compound oxalate over a period of 22 days to estimate interactions between OTUs and their environment.
Similar content being viewed by others
Introduction
Methodological advances in DNA sequencing have uncovered microbial diversity that extends far beyond that which could be detected using traditional cell culture methods. Because of the ease and inexpensive nature of new technologies, researchers are collecting increasing amounts of data with regard to various microbiomes (for example, skin, soil, gut), a trend which will only increase with newly created funding sources such as the recently announced U.S. National Microbiome Initiative (The White House Office of Science and Technology Policy, 2016). To date, most studies center around identifying members of the community using 16S rDNA sequencing and using diversity measures and ordination techniques to compare samples (Ramette, 2007; Cassman et al., 2016). While such analyses yield a large amount of information regarding where and when a particular microbe might be found, they tell almost nothing about why the microbe is there, how it interacts with its environment (for example, other microbes or hosts), and what functions it may be providing toward—or detracting from—the overall ecosystem-level services.
To address some of these central questions of interactions and function, ecological and evolutionary theory developed for macro systems has begun to be applied to microbial systems. For example, microbiome data derived from 16S rDNA sequencing has been used to estimate population dynamics of microbial communities (Marino et al., 2014), to infer how communities respond to perturbations (Stein et al., 2013), and to assess important community properties such as stability and resilience (Coyte et al., 2015). Many of the ideas that are central to microbial ecology and microbiome function are inherently dynamic and as such require longitudinal data from subjects.
Unfortunately, the staggering number of operational taxonomic units (OTUs) present in microbiomes prevents straightforward application of traditional ecological modeling methods, so methods to analyze the data have lagged behind collection. Whereas a large macro ecological system may track up to one hundred species (Montoya and Solé, 2002), microbial communities often have thousands of OTUs, which provides a significant hurdle for estimating the key interactions between microbes and other microbes and their environment. Various simplifications of data and models have been used to deal with this issue; the most common of which are to vastly reduce the size of the data by either aggregating the data at certain taxonomic levels (for example, treating Alphaproteobacteria as a model factor; McGeachie et al., 2016) or by sub-setting the data into a few taxa of interest because they are believed to be important (Hunt et al., 2011), or both (Olesen et al., 2016). Aggregation may be a particularly problematic practice because of heterogeneity within aggregated taxa. For example, estimating how Alphaproteobacteria interact with Gammaproteobacteria is akin to estimating how all dicotyledonous plants interact with monocotyledonous plants. Similarly, while focusing on only a few taxa of interest can make statistical inference techniques tractable, interactions that may actually be driving the dynamics may be left out of the model. Ecologically important forces, such as trait-mediated indirect interactions (Ridenhour and Nuismer, 2012; Berry and Widder, 2014), may be missed in this type of analysis.
Another recent method of analyzing microbiome data to infer drivers of ecological dynamics is to compare large-scale patterns. For example, Bashan et al. (2016) used patterns of dissimilarity and overlap between microbiomes to infer the degree to which interactions within a microbial community vary by environment; Bashan et al. refer to this as the ‘universality’ of microbial dynamics. While such analyses are important for a high-level understanding of dynamics, finer scale analyses are required to tease apart the underlying ecological relationships present in microbial systems. There are many examples where interspecific interactions fluctuate between antagonism and mutualism depending on the context of the interaction (Ridenhour and Nuismer, 2012), thus it seems ‘universality’ of interactions would be an unlikely feature.
Ideally, we desire ecologically relevant methods that are capable of utilizing all information gathered from sequencing to robustly infer relationships between OTUs and their environment. Methods for model estimation using data where the number of possible explanatory variables is larger than the number of observations (p≫n) typically involve the use of regularization (Tibshirani, 1996; Zou and Hastie, 2005; Meinshausen and Bühlmann, 2010) to eliminate potential explanatory variables and infer robust, stable predictive models. These regularization techniques have been successfully applied to similar data for which this problem is common, such as gene expression data and proteomics (Xing et al., 2001). Furthermore, related techniques have been applied to microbiome research. For example, Kurtz et al. (2015) applied a form of a graphical lasso procedure (sparse inverse covariance estimation; Friedman et al., 2008) to relative abundance data for entire microbiome samples. Although not experimentally validated, their study demonstrates that regularization techniques can be applied to 16S sequencing data to infer ecological networks. Regularization methods can allow for the analysis of all of the data, avoiding misleading interpretations caused by aggregating data or arbitrarily studying certain species within a microbial community.
Here, we present a novel method of analyzing 16S sequencing data that utilizes untransformed count data from the entire community and relies on regularization to infer interactions and predict future trajectories. We focus on applying this method to time-series data, which is a rapidly expanding microbiome research area and an area of special need for such techniques. We emphasize however that the methods presented here are not limited to the analysis of time series and are broadly applicable to related microbiome analyses. As an example of the power of this technique, we apply the method to gut microbiome data collected from Neotoma albigula (white-throated woodrats) during an ~3 week feeding trial in which the subjects were fed oxalate, a plant secondary defensive compound.
Materials and methods
Modeling strategy
We used an ARIMA model with Poisson errors fit with elastic-net regularization to estimate robust predictive models of microbiome dynamics. ARIMA models are commonly used in the analysis of time-series data because they provide a flexible framework that can accommodate many autocorrelation structures, stationarity conditions, and seasonality (Ives et al., 2003). The choice of Poisson distributed errors is critical to avoid issues related to compositional data: raw read counts and total read counts are the data analyzed rather than transformed compositional data. The Poisson distribution is a natural choice for count data (Anders and Huber, 2010), and, furthermore, by using the total read count as the offset in a log-linked Poisson regression model, the zeroes observed in the data are treated appropriately and have consistent meaning across variable total read counts. The resulting full model for a focal OTU is

where subscript t indicates the time of observation, x is the observed number of reads for the focal OTU, μ (to be fit by the model) is the mean of the observations x, O is the offset (for example, total number of reads or number of reads of particular taxon), X is the vector of predictor variables (that is, other OTUs, covariates, etc), ɛ is the residual error, and φ and θ are the estimated model parameters (though we are principally interested in φ because this vector contains the estimated interactions between OTUs). In the ARIMA model, p, d and q are non-negative integers that represent the number of autoregressive terms, the degree of differencing, and the number of moving average terms, respectively. Note that the number of parameters in the full model is (p+d)|X|+q; thus increasing either p or d can have large effects on the number of parameters estimated when the number of predictor variables (|X|) is large.
The full model represents a flexible way to model interactions between species that takes full advantage of the data type and its time-series structure, but would be highly overparameterized for nearly all microbial community data because of the large number of predictor OTUs. To ensure stability of the community, it is commonly held that most species interact strongly with relatively few other species (May, 1972). Some propose exponential or scale-free distributions to the number of edges in interactions networks (Fernandez et al., 2015; Kurtz et al., 2015). Regardless, the ecological expectation is that a fully saturated model, such as the one above, is not realistic. We therefore employ a regularization algorithm to select robust interaction models that have a minimal number of parameters. Elastic-net regularization is a highly flexible and rapid algorithm that penalizes both the ℓ1 and ℓ2 norms of the parameter vectors (that is, lasso and ridge regression respectively) (Tibshirani, 1996; Zou and Hastie, 2005; Draper and Pukelsheim, 2012). To estimate the parameters  , the elastic-net algorithm solves the equation
, the elastic-net algorithm solves the equation

where ℒ is the log-likelihood of the observed data (xt) given the modeled mean (μt), λ∈[0, ∞] controls the strength of the elastic-net penalty (λ=0 is equivalent to standard least squares regression), and α∈[0, 1] blends the penalty due to the ℓ1 and ℓ2 norms (α=0 is ridge regression and α=1 is lasso regression) (Tibshirani, 1996). Cross-validation techniques are used to choose optimal values for these parameters. The use of the elastic-net approach in combination with a Poisson ARIMA model allows the method to filter through large numbers of OTUs and robustly model changes in a microbiome over time.
Application of model to oxalate degradation in N. albigula
We used the modeling strategy described above to estimate microbial community dynamics from 16S rDNA time-series data collected from the white-throated woodrat, N. albigula (Miller et al., 2016). These animals were experimentally fed varying amounts of oxalate, a naturally occurring plant secondary compound that has been demonstrated to have toxic effects on a broad range of herbivores (for example, insects, mammals) (Allison et al., 1985; Dearing et al., 2005). Plants create crystalline structures known as raphides when a surplus of calcium oxalate is present; these crystals are needle-shaped and physically damage the intestinal tract of herbivores. This physical damage may also facilitate delivery of other toxins (for example, proteases) through the wall of the digestive tract (Miller et al., 2000; Franceschi and Nakata, 2005). Direct mortality, decay of the mouth and gastrointestinal tract, gastric hemorrhaging, and diarrhea have all been observed in mammals that consume large quantities of oxalate (Miller et al., 2014). Of human relevance, many kidney stones form from calcium oxalate, which may arise due to oxalate rich diets; the pain associated with passing kidney stones at least partly stems from similar needlelike structures (Miller et al., 2000; Franceschi and Nakata, 2005).
N. albigula rely on cacti, particularly Opuntia, for their diet (Justice, 1985; Miller et al., 2014), which are known to have high concentrations of calcium oxalate (Shirley and Schmidt-Nielsen, 1967). Mammals however are not known to have any mechanisms for metabolizing this toxic compound but are known to harbor bacteria capable of the task within the gut (Hodgkinson, 1977; Allison et al., 1985; Turroni et al., 2007). Prior studies of white-throated woodrats have shown that the microbiota of their gut has numerous oxalate degrading taxa including—but not limited to—Oxalobacter formigenes, Lactobacillus, Bifidobacterium, Streptococcus, and Enterococcus (Allison et al., 1985; Jones and Megarrity, 1986; Kageyama et al., 1999; Hokama et al., 2000; Sundset et al., 2010). O. formigenes has been of particular interest within the gut community because it is known to require oxalate as a carbon and energy source (Allison et al., 1985). It has been hypothesized that the specialization of and coevolution with the gut microbiome is the reason N. albigula is able to consume levels of oxalate that would be lethal for many other mammals and digest ⩾90% of this defensive compound (Shirley and Schmidt-Nielsen, 1967; James and Butcher, 1972; Justice, 1985; Palgi et al., 2008).
Feeding trials
We collected gut microbiome data from six wild-caught N. albigula trapped at Castle Valley, Utah in October 2012. Animals were transported back to the University of Utah Department of Biology Animal Facility and held in captivity for six months before experimentation. During this time, animals were fed a high-fiber rabbit chow (Teklad formula 2031; Harlan, Denver, CO, USA), which contained a baseline amount of oxalate.
Once the trial began, oxalate concentrations within the animals’ food were incrementally increased for 17 days and then dropped to the initial level for an additional five days. The amount of oxalate consumed and excreted was measured for each woodrat. Fecal pellets were collected and then underwent high-throughput 16S rDNA amplicon sequencing to determine the OTUs present in guts of the animals. OTU read counts from the cleaned and processed data were then analyzed using the model described above. A general overview of the workflow for the analyses is provided in Figure 1.
The general workflow for analyzing 16S rDNA data using a regularized ARIMA model with Poisson errors. The first several steps are the typical sequencing and bioinformatic practices where sequences are obtained and cleaned using programs such as QIIME. An additional step of dropping particularly low read count OTUs may be necessary to avoid problems with the statistical analyses reporting errors. Afterward, the cleaned data are passed to the regularization algorithm to fit an appropriate ARIMA model. The final step is to analyze the estimated interaction network (for example, heatmaps, networks, summary statistics) to interpret the models returned from the analysis.
To quantify the effect of oxalate on the gut microbiota, a custom 0.2% oxalate diet was formulated (Harlan, Denver, CO, USA) and mixed with high-fiber rabbit chow in a 3:1 ratio to give a 0.05% baseline oxalate feeding level. Additional concentrations of 0.5%, 1%, 1.5% and 3% by dry weight were achieved by adding sodium oxalate (Fisher Scientific, Pittsburgh, PA, USA) directly to the diet. The oxalate diets were given to animals in sequence for three days each, with the exception of the 0.05% oxalate diet, which was given for five days both at the beginning and the end of the diet trial. This schedule produced observations on day 5 (t0), 8 (t1), 11 (t2), 14 (t3), 17 (t4) and 22 (t5). Food and water were given ad libitum in metabolic cages, which were used to separate and collect urine and feces from each individual animal. Oxalate consumed was quantified from food intake and oxalate concentration, while oxalate excreted was quantified from urine and feces. These metrics were used to quantify total oxalate degradation, which was defined as the difference between oxalate consumed and oxalate excreted.
To track changes to the gut microbiota, feces were collected from each animal on the last day of each dietary period, thus maximizing the effect of the specified oxalate concentration on the gut microbiota. Feces were collected from the top of the 50 ml conical tube to ensure minimal exposure to aerobic conditions, and immediately frozen at −80 °C until DNA extraction. DNA extractions were performed with the QIAamp DNA stool minikit (Qiagen, Germantown, MD, USA). Microbial inventories were generated by amplifying the V4 region of the 16S rDNA gene with primers 515F and 806R (Caporaso et al., 2012) on an Illumina MiSeq at Argonne National Laboratory (Chicago, IL, USA).
The ARIMA(1,0,0) model applied to these data requires pairs of consecutive time points. Thus, for these observations there are five pairs of consecutive time points for the six animals giving a total of 30 pairs of consecutive time points. Sequence data from 4 of the 36 observations were not obtained because they had fewer than 10 000 total sequence reads, leaving a total of 23 pairs of consecutive time points for the 6 animals. The accession number for the raw data, submitted to the Sequence Read Archive, is SRR5249829.
Data processing
Sequence data were processed and demultiplexed in QIIME (Caporaso et al., 2010) using the default quality control parameters. Sequences were binned into OTUs with a de novo picking strategy using UCLUST (Edgar, 2010) at a minimum sequence identity of 97%. Chimeras were removed with ChimeraSlayer (Haas et al., 2011) along with sequences identified as chloroplasts or mitochondria.
Computational details
All statistical analyses were performed using R v3.2.2 (R Core Team, 2014) with glmnet v2.0-2 (Friedman et al., 2010), and all R scripts are available in the Supplementary Information. Before beginning the analyses, we eliminated any OTUs in the data for which there were a small number (<6) of average reads per sample because they lacked sufficient data for statistical analysis. Eliminating these unanalyzable OTUs resulted in 90% reduction in the number of OTUs giving a microbial community with 624 OTUs for modeling. The rationale for this cleaning is that there must be enough data for an OTU to successfully run a statistical model; if there is too little variation among samples for an OTU, then fitting the statistical model will fail as there is no information.
The glmnet function in the glmnet package has a number of options for performing model regularization. The most important parameters are λ and α which control the penalization. To find an optimal combination of these parameters, we used the built in cross-validation function provided in the glmnet package (‘cv.glmnet’) to loop across various levels of λ (100 values by default). We simultaneously looped across levels of α ranging from 0.5 to 1.0 in steps of 0.1. Because the cross-validation step performs K-fold cross-validation, the data folds are random; we therefore ran 500 replicates per α level to get the average cross-validated deviance for a particular α, λ combination. The best model was chosen for each α level, and the final model was chosen by utilizing AIC values and comparing between those best models. Other methods exist for choosing this parameter combination (see the c060 R package by,Sill et al., 2014 for an example of another method), but testing various algorithms is beyond the scope of this article. Other than the choice of λ and α, default parameter settings were passed to glmnet, with the exception of the ‘grouped=FALSE’ argument to ensure enough observations per fold in the default 10-fold cross-validation scheme. We verified the ability of this approach to reliably estimate model structure and parameters by testing the method in synthetic data (Supplementary Information). Generally, we found the method to be quite robust, with the caveat that underpowered studies may suffer lower sensitivity in detecting interactions.
We performed two different variants of the model. The first of these was a model in which oxalate consumption was forced to be a variable within the model (that is, oxalate consumption was a parameter that was not subject to the regularization penalties). The justification behind forcing this variable is that the experiment was designed to detect the influence of oxalate on the gut microbiome of the subjects. For comparison purposes, a second model was run where oxalate consumption was part of the regularization scheme and thus could either remain in, or be left out of, the final model chosen by the glmnet algorithm. These two models represent common research scenarios: determining effects of a particular factor that was experimentally manipulated and ‘natural’ experiments where potential covariates change in an uncontrolled manner.
Post-analysis cleaning of models for interpretation purposes was minimal. Models having a pseudo-R2 <0.02 were discarded from the results; doing so eliminated models for 154 OTUs. Effect sizes were determined by multiplying the mean OTU read counts by the corresponding estimated parameter  . Estimated observation rates were calculated using the predict function in R. The Greengenes bacterial taxonomy database ‘gg_13_5_taxonomy’ was searched to identify the phylogenetic relatedness of taxa identified in this study. The R package ape v3.5 (Paradis et al., 2004) was used to parse and plot the reduced Greengenes phylogeny.
. Estimated observation rates were calculated using the predict function in R. The Greengenes bacterial taxonomy database ‘gg_13_5_taxonomy’ was searched to identify the phylogenetic relatedness of taxa identified in this study. The R package ape v3.5 (Paradis et al., 2004) was used to parse and plot the reduced Greengenes phylogeny.
Results
The experimental setup allowed us to examine how the gut microbiome of six woodrats changed over a three-week period with varying levels of oxalate consumption. We wished to infer both how OTUs within the microbial community interacted with each other, as well as to estimate how OTUs were affected by oxalate concentration. To do so, we used an ARIMA(1,0,0) (that is, an AR(1)) model structure to limit the complexity of the model given the limited number of samples. We also included exogenous covariates for the amount of oxalate consumed and subject effects in the design matrix, bringing the total number of potential explanatory variables to 631.
We will focus on the results of the model where oxalate consumption was forced into the AR(1) model and highlight differences between it and the ‘unforced’ model. The use of elastic-net regularization easily accommodated our analysis, which included 624 OTUs and 7 other potential covariates (in other trials—not shown here—the method has worked for data sets containing thousands of covariates). We applied the AR(1) model to 626 dependent variables (624 OTUs, oxalate digested, and oxalate excreted). Of these, analyses of 40 OTUs failed due to their patterns of presence/absence (typically OTUs only observed in one woodrat), thus we obtained model fits for 586 of the dependent variables. Of 586 × 631=369766 potential parameters, the elastic-net algorithm selected models that had a total of 2886 parameters (~1%); the unforced model produced 1826 parameters in comparison. Of the 586 dependent variables, 280 had a model that included additional variables from the minimal model consisting of only an intercept and oxalate consumed (295 for the unforced model). Thus, the regularization procedure produced models where there were relatively few predicted interactions between OTUs within the gut microbiome (that is, a sparse interaction matrix). As mentioned above, 154 models with low pseudo-R2 values were eliminated before further analysis; only 12 of the 154 were models consisting of something other than the forced intercept and oxalate consumed terms (that is, models that had interactions between species) leaving 268 models for the network analysis.
The estimated network of interactions between species fits the ‘small-world’ network paradigm that has been observed in many other non-microbial communities (Watts and Strogatz, 1998; Montoya and Solé, 2002). Supplementary Figure 4 shows the in- and out-degree distributions for the predicted interaction network (that is, the number of covariates affecting and affected by an OTU, respectively). These distributions fall in between what would be expected in a scale-free network and a random network. The average path length in the estimated network is L=0.441, whereas a similar random network would have an average path length of Lrandom≈0.222. The average clustering coefficient (transitivity) of the estimated interaction network is C=0.285 which compares to Crandom≈0.038 in the random network. Therefore, our network fits the definition of a small world where LSW⩾Lrandom and CSW≫Crandom (Jordano et al., 2003). Path lengths and clustering coefficients were calculated using weighted edges based on the estimated strength of an interaction (that is,  ; using unweighted edges does not qualitatively change the interpretation of the network. Small-world patterns of interaction are hypothesized to add stability to the community as a whole (that is, small neighborhoods/clusters of species may fail or fluctuate without much effect on the whole community) (May, 1972; Polis, 1998 McCann, 2000). This network structure also implies that a few species (‘hubs’) interact with many others and are critical to stability, thus fitting the keystone species concept (Faust and Raes, 2012). However, other research provides counterarguments to the hypothesis that more structured, small-world networks increase stability (Sinha, 2005).
; using unweighted edges does not qualitatively change the interpretation of the network. Small-world patterns of interaction are hypothesized to add stability to the community as a whole (that is, small neighborhoods/clusters of species may fail or fluctuate without much effect on the whole community) (May, 1972; Polis, 1998 McCann, 2000). This network structure also implies that a few species (‘hubs’) interact with many others and are critical to stability, thus fitting the keystone species concept (Faust and Raes, 2012). However, other research provides counterarguments to the hypothesis that more structured, small-world networks increase stability (Sinha, 2005).
We assessed the fit of models using a pseudo-R2 metric based on the percentage of the deviance explained by the model (Cameron and Windmeijer, 1997). Figure 2 shows the distribution of pseudo-R2 values for the fitted models. Models with a high pseudo-R2 predict the dynamics of a particular OTU better than models with relatively lower pseudo-R2 (Figures 2 and 3). A broad range of values were returned that spanned all possible values (that is, 0 to 1). Importantly, we found that the pseudo-R2 values did not depend on the α parameter of the elastic-net regularization, which influences the number of parameters (that is, interactions with other OTUs) in the model (Figure 2). The dynamic patterns predicted by the model match expectations based on previous work on the effects of oxalate on the gut microbiome (Miller et al., 2014, 2016). For example, Oxalobacter were predicted to increase with increasing oxalate consumption over the first 5 weeks and then decrease after test subjects were no longer fed oxalate.
Distribution of pseudo-R2 values and their relationship to the elastic-net mixing parameter α from the models fit for woodrat gut microbiome data. The left panel shows that the method returned a fairly uniform distribution of values, that is, we observed the full spectrum of poorly fitting models to very good models. The mixing parameter α alters the regularization penalty to favor either more small parameters (low α) or fewer large parameters (large α) in the model. The dotted red line shows the smoothed mean of the pseudo-R2 values across α-levels; the blue line shows the result of fitting a third order polynomial using linear regression (R2=0.2382, P<0.001). The relationship between α (roughly, the number of parameters) and the pseudo-R2 for the AR(1) models had a positive first-order term indicating better model fits were achieved for models with fewer parameters; this observed trend however peaked at α≈0.86 and then reversed.
Predicted (lines) and measured (points) OTU observation rates in the woodrat gut microbiome over the 22-day feeding the trial for three representative OTUs. Colors indicate different test subjects; some lines are incomplete because only points where data were available for the subject for t−1 and t are plotted (that is, those data to which an AR(1) model could be applied; this is why t0 is omitted). Note that each panel shows a single OTU from the family S24-7, not the aggregation of all OTUs within S24-7 (that is, each is a separate OTU given a ‘de novo’ label). The panels from upper to lower are ordered by decreasing pseudo-R2 with values of 0.99, 0.54 and 0.22, respectively. See Methods for detailed observation times.
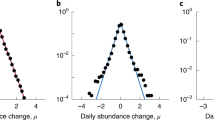
Oxalate consumption clearly has a broad range of effects on bacteria in the N. albigula gut (Tables 1 and 2). Figure 4 shows the distribution of these effects across all OTUs, as well as the effects on oxalate excreted and digested. For the unforced model, only 10 OTUs were predicted to be affected by oxalate consumption. The results of the analysis of the woodrat data support previous findings with respect to the consumption of oxalate (Miller et al., 2014, 2016). For example, we found that increased consumption of oxalate leads to increased numbers of Oxalobacter, Oxalobacteraceae, and Clostridiales within the gut (Table 2). These taxa are known degraders of oxalate (Miller et al., 2014). However, we also found that other OTUs—such as some members of the families S24-7, Helicobacter, and Lachnospiraceae—are more positively affected by oxalate consumption than these well-known oxalate degraders (Tables 1 and 2). One possible explanation is that these taxa have uncharacterized oxalate degrading capacity or homologs of oxalyl-CoA decarboxylase (Sahin, 2003; Werther et al., 2010). Even in strains isolated from N. albigula, Miller et al., (2014) find species that can degrade oxalate in vitro may lack the oxalyl-CoA decarboxylase gene. Another explanation for why the effect of oxalate consumption may have been overlooked may be due to grouping OTUs together within particular taxonomic IDs. For example, while multiple OTUs within the family S24-7 are strongly positively affected by oxalate consumption, several are also strongly negatively affected (Table 1); thus, the mean effect of oxalate consumption on S24-7 is lower than that of other OTUs (Table 2) and would be overlooked in studies that aggregate OTUs. For comparative purposes, aggregated effect sizes between unique taxonomic groupings are plotted in Figure 5.
Distributions of oxalate effect sizes ( ). The top panel shows the distribution of effect sizes for all OTUs for which a model was successfully fit in the woodrat gut microbiome study. The middle panel shows the distribution of estimated effect sizes for the 36 OTUs whose lowest taxonomic designation was Ruminococcaceae; the dotted vertical (red) line is the mean of those estimated effects. The bottom panel shows the distribution of mean effect sizes (
). The top panel shows the distribution of effect sizes for all OTUs for which a model was successfully fit in the woodrat gut microbiome study. The middle panel shows the distribution of estimated effect sizes for the 36 OTUs whose lowest taxonomic designation was Ruminococcaceae; the dotted vertical (red) line is the mean of those estimated effects. The bottom panel shows the distribution of mean effect sizes ( ) for the 38 unique taxonomic IDs to which the OTUs were assigned (see Table 2 for extreme values related to the bottom panel).
) for the 38 unique taxonomic IDs to which the OTUs were assigned (see Table 2 for extreme values related to the bottom panel).
Mean pairwise effect sizes of interacting factors. The direction of the interactions is such that the factors on the horizontal axis affect the variables on the vertical axis (which are arranged by taxonomic classification per the Greengenes database). The scaled colors indicate the magnitude and direction of the interaction between the two variables.
Our results corroborate empirical work showing sparse distributions of oxalate degrading capacity among bacterial phylogenies, even at the species or strain level (Turroni et al., 2010; Ren et al., 2011; Miller et al., 2014; Ormerod et al., 2016). For example, our results suggest that S24-7 strains can be positively or negatively affected by oxalate. Ormerod et al. show by using genome sequencing that oxalate degradation pathways are present in only 19 of 30 S24-7 (renamed Ca. Homeothermaceae) isolates from human, mouse, koala, and guinea pig samples (Ormerod et al., 2016). The presence of these pathways does not correlate with host taxonomy, but rather, both oxalate degraders and non-degraders are present in all host types.
Discussion
We have presented a method for the analysis of microbial community data that leverages the power of regularization techniques to infer ecological interactions and predict dynamics based on OTU-level 16S rDNA read counts and applied the method to time-series microbiome data from an oxalate feeding trial in woodrats. This modeling strategy for 16S rDNA amplicon data provides a flexible and relatively computationally inexpensive method for researchers to estimate the strength of ecological interactions in microbial communities. By modeling read count data directly and using elastic-net regularization to select and stabilize the model, the method overcomes many common challenges in analyzing microbiome data.
The vast diversity of taxa that occurs in most microbiomes (Shade et al., 2014; Coyte et al., 2015) poses an enormous challenge in studying ecological dynamics of these systems. Computational barriers make it impossible to apply many traditional methods of statistical analysis to such large, complex systems. In order to make analyses tractable, researchers typically reduce the number of OTUs being studied to just a handful that are of interest (Buffie et al., 2015) or to those with the largest relative abundance (Vahjen et al., 2011; Marino et al., 2014). Both of these options may provide answers that are biased a priori. By limiting the study to OTUs of interest, it is impossible to discover new roles for microbes within communities because ‘uninteresting’ OTUs would never be studied. Similarly, by only analyzing the numerically dominant species, important roles of microbes whose abundance falls below the cutoff will not be investigated; it is well-known from community ecology that keystone species for communities need not be numerically dominant species (Shade et al., 2014). Regularization combined with appropriate mathematical models provides a framework to analyze the entirety of the data, rather than arbitrarily selecting OTUs of interest.
Typically, amplicon data are transformed to represent relative abundances within a community by dividing the number of reads by the total number of reads in the sample (Human Microbiome Project Consortium, 2012); this normalization leads to numerous statistical complications, the two most prominent being altering the correlation structure of the data and censoring of the data at some arbitrary level (Hinkle and Rayens, 1995; Egozcue et al., 2003; van den Boogaart and Tolosana-Delgado, 2008; Li, 2015). Compositional data, data whose sum is forced to be one, have a different correlation structure which can mask the true nature of the interactions between species (Lin et al., 2014). For example, if one OTU's relative abundance increases, it is impossible to distinguish a hypothesis of a true increase in absolute abundance from a hypothesis of a net decrease in absolute abundance of the other members of the community. Various transformations (for example, isometric log-ratio, centered log-ratio) have been applied to correct for this, but, while they provide improvements, complete resolution of this forced correlation structure by transformation is unlikely (Egozcue et al., 2003). Using Poisson regression ameliorates—but does not completely alleviate—the inherent correlation structure of compositional data; more complex methods using, for example, multinomial or multivariate Poisson-log normal distributions could entirely correct for the correlation structure (Aitchison and Ho, 1989).
An additional complexity for relative abundance data relates to what a zero relative abundance actually means. For example, if one sample had 100 total reads while another had 1000 total reads, then a zero from the first sample represents <0.01 compared with <0.001 for the second. Issues regarding the analysis of censored data are well documented (Hinkle and Rayens, 1995; Egozcue et al., 2003; Li, 2015), and methods are available to correct these issues (Freeman and Modarres, 2002; Lin et al., 2014); the methods however are often computationally expensive (for example, bootstrapping models over imputed values) which is problematic given the already large size and complexity of the analyses, and may never fully resolve the censoring issues. Modeling the read count data directly—as suggested herein—rather than data that has been normalized to relative abundance overcomes these statistical issues.
While we have chosen to model only the linear (first-order) terms as an AR(1) model for the woodrat gut microbiome, the ARIMA model can be modified to accommodate complex dynamics (for example, seasonality) in a system by adjusting p, d, or q. If data quantity and quality is sufficient, more complex ARIMA models may provide better predictions of future dynamics, though interpretation of the interaction parameters becomes more difficult as the complexity of the model increases. Higher order terms that test for complex interactions (such a trait-mediated indirect interactions) could also be included with the caveat that altering the structure of the ARIMA or the order of the predictor terms can greatly increase the number of parameters, thus exacerbating the problem that the number of possible parameters is far greater than the number of observations. As a whole, the study of microbiome dynamics needs continued advances in modeling strategies to successfully understand the eco-evolutionary complexity of microbial communities, where higher order interactions are likely to be the rule rather than the exception.
Other recent methods such as LIMITS and MDSINE can be used to estimate a Lotka-Volterra model of microbial dynamics (Fisher and Mehta, 2014; Bucci et al., 2016). The method presented here shares some similarities to these approaches: Any method to estimate microbial interactions and dynamics will require (1) an underlying model (for example, ARIMA or generalized Lotka-Volterra) and (2) regularization (for example, ridge, lasso or elastic-net) to correct for the p≫n problem. In contrast, the proposed underlying ARIMA model is able to accommodate a wider range of complex dynamics and error structure. However, coefficients from higher order ARIMA models may be harder to interpret biologically.
It is important to realize that, while the methods presented here can be adapted to address many questions, the quality and amount of data collected strongly influences the quality of the results. For example, Kurtz et al. (2015) examined the ability to recover certain synthetic network types (for example, scale-free versus clustered networks) from different regularization algorithms and show how the ability to recover edges (interactions) in the network is dependent on the number of samples, a point shared in our analysis of simulated data (Supplementary Information). Our analysis of simulated data also shows that a threshold can be applied to the magnitude of inferred interactions to potentially improve the sensitivity and specificity of edge detection for underpowered studies. In addition to the number of samples, the degree to which samples vary greatly influences the amount of information they contain regarding dynamics; collecting samples at a time resolution sufficient to capture the variation will yield the most information. Similarly, measurements must capture the key drivers of the dynamics; if unmeasured variables such as diet or environmental conditions strongly influence the microbial dynamics and these factors are not included in the model, estimates of interactions may be misleading. Beyond issues concerning data quality and quantity, tuning the model and algorithm parameters (for example, see the method of cross-validation in Computational Details) has important consequences for the resulting inference. Thus, as with any statistical analysis, it is important to examine diagnostic outputs of the models to ascertain proper performance of the method.
The combination of using an (elastic-net) regularized ARIMA model with Poisson errors tackles many issues facing the analysis of microbiome time-series data and is flexible enough to be adapted to other types of analyses. For example, while we have chosen to use Poisson distributed errors it would be easy to switch this distribution to others that are commonly used for count data, such as either the quasipoisson or negative binomial distribution to handle overdispersion in amplicon counts (though the point estimates for the parameters are nearly identical for the Poisson, quasipoisson, and negative binomial models). As demonstrated in the oxalate analysis, if the experimental design is such that it is logical to force the inclusion of certain variable(s), this can be done within the regularization algorithm; the same can be said for inclusion or exclusion of an intercept term in the model. The general method of using regularization along with Poisson errors can be applied to more basic microbiome analyses as well. For example, to ask the question of which OTUs might contribute to a particular observation of interest (for example, which OTUs in the gut microbiome are predictive of obesity), the ARIMA equations present above could be replaced by the familiar regression equation y=Xβ.
As the amount of information related to the ecology and evolution of microbial communities increases, scalable methods of statistical analysis such as the method presented here will be required to make sense of data. By utilizing regularization and a model with error structure designed for count data, this method overcomes many obstacles to interpreting microbiome dynamics, providing a needed framework to address important eco-evolutionary questions regarding microbial communities.
References
Aitchison J, Ho CH . (1989). The multivariate Poisson-log normal distribution. Biometrika 76: 643–653.
Allison MJ, Dawson KA, Mayberry WR, Foss JG . (1985). Oxalobacter formigenes gen. nov., sp. nov.: oxalate-degrading anaerobes that inhabit the gastrointestinal tract. Arch Microbiol 141: 1–7.
Anders S, Huber W . (2010). Differential expression analysis for sequence count data. Genome Biology 11: 1.
Bashan A, Gibson TE, Friedman J, Carey VJ, Weiss ST, Hohmann EL et al. (2016). Universality of human microbial dynamics. Nature 534: 259–262.
Berry D, Widder S . (2014). Deciphering microbial interactions and detecting keystone species with co-occurrence networks. Front Microbiol 5: 219.
Bucci V, Tzen B, Li N, Simmons M, Tanoue T, Bogart E et al. (2016). MDSINE: Microbial Dynamical Systems INference Engine for microbiome time-series analysis. Genome Biol 17: 121.
Buffie CG, Bucci V, Stein RR, McKenney PT, Ling L, Gobourne A et al. (2015). Precision microbiome reconstitution restores bile acid mediated resistance to Clostridium difficile. Nature 517: 205–208.
Cameron AC, Windmeijer FA . (1997). An R-squared measure of goodness of fit for some common nonlinear regression models. J Econom 77: 329–342.
Caporaso JG, Kuczynski J, Stombaugh J, Bittinger K, Bushman FD, Costello EK et al. (2010). QIIME allows analysis of high-throughput community sequencing data. Nat Methods 7: 335–336.
Caporaso JG, Lauber CL, Walters WA, Berg-Lyons D, Huntley J, Fierer N et al. (2012). Ultra-high-throughput microbial community analysis on the Illumina HiSeq and MiSeq platforms. ISME J 6: 1621–1624.
Cassman NA, Leite MFA, Pan Y, de Hollander M, van Veen JA, Kuramae EE . (2016). Plant and soil fungal but not soil bacterial communities are linked in long-term fertilized grassland. Sci Rep 6: 23680.
Coyte KZ, Schluter J, Foster KR . (2015). The ecology of the microbiome: networks, competition, and stability. Science 350: 663–666.
Dearing MD, Foley WJ, McLean S . (2005). The influence of plant secondary metabolites on the nutritional ecology of herbivorous terrestrial vertebrates. Annu Rev Ecol Evol Syst 36: 169–189.
Draper NR, Pukelsheim F . (2012). Generalized ridge analysis under linear restrictions, with particular applications to mixture experiments problems. Technometrics 44: 250–259.
Edgar RC . (2010). Search and clustering orders of magnitude faster than BLAST. Bioinformatics 26: 2460–2461.
Egozcue JJ, Pawlowsky-Glahn V, Mateu-Figueras G, Barcelo-Vidal C . (2003). Isometric logratio transformations for compositional data analysis. Math Geol 35: 279–300.
Faust K, Raes J . (2012). Microbial interactions: from networks to models. Nat Rev Micro 10: 538–550.
Fernandez M, Riveros JD, Campos M, Mathee K, Narasimhan G . (2015). Microbial “social networks”. BMC Genomics 16: S6.
Fisher CK, Mehta P . (2014). Identifying keystone species in the human gut microbiome from metagenomic timeseries using sparse linear regression. PLoS One 9: e102451.
Franceschi VR, Nakata PA . (2005). Calcium oxalate in plants: formation and function. Annu Rev Plant Biol 56: 41–71.
Freeman J, Modarres R . (2002) Analysis of Censored Environmental Data with Box-Cox Transformations.
Friedman J, Hastie T, Tibshirani R . (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9: 432–441.
Friedman J, Hastie T, Tibshirani R . (2010). Regularization paths for generalized linear models via coordinate descent. J Stat Softw 33: 1–22.
Haas BJ, Gevers D, Earl AM, Feldgarden M, Ward DV, Giannoukos G et al. (2011). Chimeric 16S rRNA sequence formation and detection in Sanger and 454-pyrosequenced PCR amplicons. Genome Res 21: 494–504.
Hinkle J, Rayens W . (1995). Partial least squares and compositional data: problems and alternatives. Chemometr Intell Lab Syst 30: 159–172.
Hodgkinson A . (1977) Oxalic Acid in Biology and Medicine. Academic Press: London.
Hokama S, Honma Y, Toma C, Ogawa Y . (2000). Oxalate-degrading Enterococcus faecalis. Microbiol Immunol 44: 235–240.
Holmes EE, Ward EJ, Wills K . (2012). MARSS: multivariate autoregressive state-space models for analyzing time-series data. R J 4: 11–19.
Human Microbiome Project Consortium. (2012). Structure, function and diversity of the healthy human microbiome. Nature 486: 207–214.
Hunt KM, Foster JA, Forney LJ, Schütte UM, Beck DL, Abdo Z et al. (2011). Characterization of the diversity and temporal stability of bacterial communities in human milk. PloS One 6: e21313.
Ives A, Dennis B, Cottingham K, Carpenter S . (2003). Estimating community stability and ecological interactions from time-series data. Ecol Monogr 73: 301–330.
James LF, Butcher JE . (1972). Halogeton poisoning of sheep: effect of high level oxalate intake. J Anim Sci 35: 1233–1238.
Jones R, Megarrity R . (1986). Successful transfer of DHP-degrading bacteria from Hawaiian goats to Australian ruminants to overcome the toxicity of Leucaena. Aust Vet J 63: 259–262.
Jordano P, Bascompte J, Olesen JM . (2003). Invariant properties in coevolutionary networks of plant–animal interactions. Ecol Lett 6: 69–81.
Justice KE . (1985). Oxalate digestibility in Neotoma albigula and Neotoma mexicana. Oecologia 67: 231–234.
Kageyama A, Benno Y, Nakase T . (1999). Phylogenetic evidence for the transfer of Eubacterium lentum to the genus Eggerthella as Eggerthella lenta gen. nov., comb. nov. Int J Syst Evol Microbiol 49: 1725–1732.
Kurtz ZD, Müller CL, Miraldi ER, Littman DR, Blaser MJ, Bonneau RA . (2015). Sparse and compositionally robust inference of microbial ecological networks. PLoS Comput Biol 11: e1004226.
Li H . (2015). Microbiome, metagenomics, and high-dimensional compositional data analysis. Annu Rev Stat Appl 2: 73–94.
Lin W, Shi P, Feng R, Li H . (2014). Variable selection in regression with compositional covariates. Biometrika 101: 785–797.
Marino S, Baxter N, Huffnagle G, Petrosino J, Schloss P . (2014). Mathematical modeling of primary succession of murine intestinal microbiota. Proc Natl Acad Sci USA 111: 439–444.
May R . (1972). Will a large complex system be stable? Nature 238: 413–414.
McCann KS . (2000). The diversity-stability debate. Nature 405: 228–233.
McGeachie MJ, Sordillo JE, Gibson T, Weinstock GM, Liu YY, Gold DR et al. (2016). Longitudinal prediction of the infant gut microbiome with dynamic Bayesian networks. Sci Rep 6: 20359.
Meinshausen N, Bühlmann P . (2010). Stability selection. J R Stat Soc Ser B 72: 417–473.
Miller AW, Kohl KD, Dearing MD . (2014). The gastrointestinal tract of the white-throated woodrat (Neotoma albigula harbors distinct consortia of oxalate-degrading bacteria. Appl Environ Microbiol 80: 1595–1601.
Miller AW, Oakeson KF, Dale C, Dearing MD . (2016). Effect of dietary oxalate on the gut microbiota of the mammalian herbivore Neotoma albigula. Appl Environ Microbiol 82: 2669–2675.
Miller C, Kennington L, Cooney R, Kohjimoto Y, Cao LC, Honeyman T et al. (2000). Oxalate toxicity in renal epithelial cells: characteristics of apoptosis and necrosis. Toxicol Appl Pharmacol 162: 132–141.
Montoya JM, Solé RV . (2002). Small world patterns in food webs. J Theor Biol 214: 405–412.
Olesen SW, Vora S, Techtmann SM, Fortney JL, Bastidas-Oyanedel JR, Rodríguez J et al. (2016). A novel analysis method for paired-sample microbial ecology experiments. PLoS One 11: e0154804.
Ormerod KL, Wood DL, Lachner N, Gellatly SL, Daly JN, Parsons JD et al. (2016). Genomic characterization of the uncultured Bacteroidales family S24-7 inhabiting the guts of homeothermic animals. Microbiome 4: 36.
Palgi N, Ronen Z, Pinshow B . (2008). Oxalate balance in fat sand rats feeding on high and low calcium diets. J Comp Physiol B 178: 617–622.
Paradis E, Claude J, Strimmer K . (2004). APE: analyses of phylogenetics and evolution in R language. Bioinformatics 20: 289–290.
Polis G . (1998). Stability is woven by complex webs. Nature 395: 744–745.
R Core Team. (2014) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria, 2013.
Ramette A . (2007). Multivariate analyses in microbial ecology. FEMS Microbiol Ecol 62: 142–160.
Ren Z, Pan C, Jiang L, Wu C, Liu Y, Zhong Z et al. (2011). Oxalate-degrading capacities of lactic acid bacteria in canine feces. Vet Microbiol 152: 368–373.
Ridenhour BJ, Nuismer SL . (2012) Perspective: trait-mediated indirect interactions and the coevolutionary processIn: Ohgushi T, Schmitz OJ, Holt RD (eds.) Trait-mediated Indirect Interactions: Ecological and Evolutionary Perspectives. Cambridge University Press: Cambridge, UK, pp 207–220.
Sahin N . (2003). Oxalotrophic bacteria. Res Microbiol 154: 399–407.
Shade A, Jones SE, Caporaso JG, Handelsman J, Knight R, Fierer N et al. (2014). Conditionally rare taxa disproportionately contribute to temporal changes in microbial diversity. MBio 5: e01371–14.
Shirley EK, Schmidt-Nielsen K . (1967). Oxalate metabolism in the pack rat, sand rat, hamster, and white rat. J Nutr 91: 496–502.
Sill M, Hielscher T, Becker N, Zucknick M et al. (2014). C060: extended inference with lasso and elastic-net regularized Cox and generalized linear models. J Stat Softw 62: 1–22.
Sinha S . (2005). Complexity vs. stability in small-world networks. Physica A 346: 147–153.
Stein RR, Bucci V, Toussaint NC, Buffie CG, Rätsch G, Pamer EG et al. (2013). Ecological modeling from time-series inference: insight into dynamics and stability of intestinal microbiota. PLoS Comput Biol 9: e1003388.
Sundset MA, Barboza PS, Green TK, Folkow LP, Blix AS, Mathiesen SD . (2010). Microbial degradation of usnic acid in the reindeer rumen. Naturwissenschaften 97: 273–278.
The White House Office of Science and Technology Policy. (2016), National Microbiome Initiative.
Tibshirani R . (1996). Regression shrinkage and selection via the lasso. J R Stat Soc Ser B 58: 267–288.
Turroni S, Bendazzoli C, Dipalo SC, Candela M, Vitali B, Gotti R et al. (2010). Oxalate-degrading activity in Bifidobacterium animalis subsp. lactis: Impact of acidic conditions on the transcriptional levels of the oxalyl coenzyme A (CoA) decarboxylase and formyl-CoA transferase genes. Appl Environ Microbiol 76: 5609–5620.
Turroni S, Vitali B, Bendazzoli C, Candela M, Gotti R, Federici F et al. (2007). Oxalate consumption by lactobacilli: evaluation of oxalyl-CoA decarboxylase and formyl-CoA transferase activity in Lactobacillus acidophilus. J Appl Microbiol 103: 1600–1609.
Vahjen W, Pieper R, Zentek J . (2011). Increased dietary zinc oxide changes the bacterial core and enterobacterial composition in the ileum of piglets. J Anim Sci 89: 2430–2439.
van den Boogaart KG, Tolosana-Delgado R . (2008). “Compositions”: a unified R package to analyze compositional data. Comput Geosci 34: 320–338.
Watts DJ, Strogatz SH . (1998). Collective dynamics of 'small-world' networks. Nature 393: 440–442.
Werther T, Zimmer A, Willie G, Golbik R, Weiss MS, König S . (2010). New insights into structure–function relationships of oxalyl CoA decarboxylase from Escherichia coli. FEBS J 277: 2628–2640.
Xing EP, Jordan MI, Karp RM . (2001), Feature selection for high-dimensional genomic microarray data. In: Proceedings of the eighteenth international conference on machine learning. Morgan Kaufmann, pp. 601–608.
Zou H, Hastie T . (2005). Regularization and variable selection via the elastic net. J R Stat Soc Ser B 67: 301–320.
Acknowledgements
We thank Jodie Nicotra for help with comments and edits on the manuscript as well as members of CMCI, IBEST and BCB at the University of Idaho for helpful discussions on the research topic. Research reported in this publication was partially supported by the National Institute Of General Medical Sciences of the National Institutes of Health under Award Numbers P20GM104420 and P30GM103324 to University of Idaho. Funding was also provided in part by NSF DEB-1342615 to M.D. and Johnson and Johnson to B.R. The content is solely the responsibility of the authors and does not necessarily represent the official views of the sponsoring agencies.
Author contributions
BR and CR conceived the modeling; AM and MD conceived the feeding experiment; AM performed the feeding experiment; BR conducted all analyses; SB, JW and JVL helped refine the modeling procedures and prepare the manuscript. All authors reviewed the manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on The ISME Journal website
Rights and permissions
About this article
Cite this article
Ridenhour, B., Brooker, S., Williams, J. et al. Modeling time-series data from microbial communities. ISME J 11, 2526–2537 (2017). https://doi.org/10.1038/ismej.2017.107
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/ismej.2017.107
This article is cited by
-
Microbial trend analysis for common dynamic trend, group comparison, and classification in longitudinal microbiome study
BMC Genomics (2021)
-
Application of OU processes to modelling temporal dynamics of the human microbiome, and calculating optimal sampling schemes
BMC Bioinformatics (2020)
-
An expectation-maximization algorithm enables accurate ecological modeling using longitudinal microbiome sequencing data
Microbiome (2019)
-
MetaLonDA: a flexible R package for identifying time intervals of differentially abundant features in metagenomic longitudinal studies
Microbiome (2018)