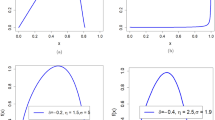
Abstract
Background/Objectives:
Conventional statistical methods often test for group differences in a single parameter of a distribution, usually the conditional mean (for example, differences in mean body mass index (BMI; kg m−2) by education category) under specific distributional assumptions. However, parameters other than the mean may of be interest, and the distributional assumptions of conventional statistical methods may be violated in some situations.
Subjects/Methods:
We describe an application of the generalized lambda distribution (GLD), a flexible distribution that can be used to model continuous outcomes, and simultaneously describe a likelihood ratio test for differences in multiple distribution parameters, including measures of central tendency, dispersion, asymmetry and steepness. We demonstrate the value of our approach by testing for differences in multiple parameters of the BMI distribution by education category using the Health and Retirement Study data set.
Results:
Our proposed method indicated that at least one parameter of the BMI distribution differed by education category in both the complete data set (N=13 571) (P<0.001) and a randomly resampled data set (N=300 from each category) to assess the method under circumstances of lesser power (P=0.044). Similar method using normal distribution alternative to GLD indicated the significant difference among the complete data set (P<0.001) but not in the smaller randomly resampled data set (P=0.968). Moreover, the proposed method allowed us to specify which parameters of the BMI distribution significantly differed by education category for both the complete and the random subsample, respectively.
Conclusions:
Our method provides a flexible statistical approach to compare the entire distribution of variables of interest, which can be a supplement to conventional approaches that frequently require unmet assumptions and focus only on a single parameter of distribution.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Peeters A, Gearon E, Backholer K, Carstensen B . Trends in the skewness of the body mass index distribution among urban Australian adults, 1980 to 2007. Ann Epidemiol 2015; 25: 26–33.
Komlos J, Brabec M . The trend of BMI values of US adults by deciles, birth cohorts 1882-1986 stratified by gender and ethnicity. Econ Hum Biol 2011; 9: 234–250.
Beyerlein A . Quantile regression-opportunities and challenges from a user's perspective. Am J Epidemiol 2014; 180: 330–331.
Redden DT, Fernandez JR, Allison DB . A simple significance test for quantile regression. Stat Med 2004; 23: 2587–2597.
Beyerlein A, Toschke AM, von Kries R . Breastfeeding and childhood obesity: shift of the entire BMI distribution or only the upper parts? Obesity (Silver Spring) 2008; 16: 2730–2733.
Garn SM, Sullivan TV, Hawthorne VM . Educational level, fatness, and fatness differences between husbands and wives. Am J Clin Nutr 1989; 50: 740–745.
Tavani A, Negri E, La Vecchia C . Determinants of body mass index: a study from northern Italy. Int J Obes Relat Metab Disord 1994; 18: 497–502.
Hermann S, Rohrmann S, Linseisen J, May AM, Kunst A, Besson H et al. The association of education with body mass index and waist circumference in the EPIC-PANACEA study. BMC Public Health 2011; 11: 169.
Zhang Q, Wang Y . Trends in the association between obesity and socioeconomic status in US adults: 1971 to 2000. Obes Res 2004; 12: 1622–1632.
Molarius A, Seidell JC, Sans S, Tuomilehto J, Kuulasmaa K . Educational level, relative body weight, and changes in their association over 10 years: an international perspective from the WHO MONICA Project. Am J Public Health 2000; 90: 1260–1268.
Mujahid MS, Diez Roux AV, Borrell LN, Nieto FJ . Cross-sectional and longitudinal associations of BMI with socioeconomic characteristics. Obes Res 2005; 13: 1412–1421.
Jolliffe D . Overweight and poor? On the relationship between income and the body mass index. Econ Hum Biol 2011; 9: 342–355.
RAND. RAND HRS Data, Version M. RAND Center for the Study of Aging, with funding from the National Institute on Aging and the Social Security Administration: Santa Monica, CA, USA 2013.
Chalabi Y, Scott DJ, Wuertz D . Flexible distribution modeling with the generalized lambda distribution. MPRA 2012; 43333 Available at: https://mpra.ub.uni-muenchen.de/43333/.
Ozturk A, Dale R . A study of fitting the generalized lambda distribution to solar-radiation data. J Appl Meteorol 1982; 21: 10.
Demirtas H . Multiple imputation under the generalized lambda distribution. J Biopharm Stat 2009; 19: 77–89.
Neyman J, Pearson ES . On the problem of the most efficient tests of statistical hypotheses. Philos Trans R Soc Lond A 1933; 231: 289–337.
Pearson K . Method of moments and method of maximum likelihood. Biometrika 1936; 28: 34–59.
Su S . Fitting flexible parametric regression models with GLDreg in R. J Mod Appl Stat Methods 2016; 15: 46.
Akaike H Information theory and an extension of the maximum likelihood principle. In: Kotz S, Johnson NL, eds. Breakthroughs in Statistics: Foundations and Basic Theory. Springer: New York, NY, USA, 1992; 610–624.
Ng M, Liu P, Thomson B, Murray CJ . A novel method for estimating distributions of body mass index. Popul Health Metr 2016; 14: 6.
Acknowledgements
We thank Dr Jasmin Divers for reviewing our initial manuscript and providing constructive comments. We also thank Jennifer Holmes for editing our manuscript. This study was supported in part by NIH grants P30DK056336 and UL1TR001417, Japan Society for Promotion of Science (JSPS) grant KAKENHI 15J00009 and Grant-in-Aid for Epidemiological Research from St Luke’s International University. The opinions expressed are those of the authors and do not necessarily represent those of the NIH or any other organization.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Author contributions
KE, GP and PL prepared the original draft. KE and PL led the data analysis. GP conducted the literature search and managed the data. DBA conceived and supervised the project.
Supplementary Information accompanies this paper on International Journal of Obesity website
Supplementary information
Rights and permissions
About this article
Cite this article
Ejima, K., Pavela, G., Li, P. et al. Generalized lambda distribution for flexibly testing differences beyond the mean in the distribution of a dependent variable such as body mass index. Int J Obes 42, 930–933 (2018). https://doi.org/10.1038/ijo.2017.262
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/ijo.2017.262