Abstract
The stacking order in layered transition-metal dichalcogenides (TMDCs) induces variations in the electronic and interlayer couplings. Therefore, controlling the stacking orientations when synthesizing TMDCs is desirable but remains a significant challenge. Here, we developed and showed the growth kinetics of different shapes and stacking orders in as-grown multi-stacked MoS2 crystals and revealed the stacking-order-induced interlayer separations, spin–orbit couplings (SOCs), and symmetry variations. Raman spectra in AA(A…)-stacked crystals demonstrated blueshifted out-of-plane (A1g) and in-plane (E2g1) phonon frequencies, representing a greater reduction of the van der Waals gap compared to conventional AB(A…)-stacking. Our observations, together with first-principles calculations, revealed distinct excitonic phenomena due to various stacking orientations. As a result, the photoluminescence emission was improved in the AA(A…)-stacking configuration. Additionally, calculations showed that the valence-band maxima (VBM) at the K point of the AA(A…)-stacking configuration was separated into multiple sub-bands, indicating the presence of stronger SOC. We demonstrated that AA(A…)-stacking emitted an intense second-harmonic signal (SHG) as a fingerprint of the more augmented non-centrosymmetric stacking and enabled SOC-induced splitting at the VBM. We further highlighted the superiority of four-wave mixing-correlated SHG microscopy to quickly resolve the symmetries and multi-domain crystalline phases of differently shaped crystals. Our study based on crystals with different shapes and multiple stacking configurations provides a new avenue for development of future optoelectronic devices.
Similar content being viewed by others
Introduction
Two-dimensional (2D) transition-metal dichalcogenides, including molybdenum disulfide (MoS2), have great potential applications in advanced electronic and optoelectronic devices.1, 2, 3, 4, 5, 6, 7, 8, 9, 10 Thus, such materials are being intensively studied with a focus on controllable synthesis with excellent optical and electrical performances. Monolayer MoS2 has a direct band-gap structure, exhibiting many intriguing physical properties, such as strong photoluminescence (PL), electronic mobility, and valley and spin polarization.1, 2, 3 Furthermore, the above optoelectronic properties can be controlled and advanced by adopting a proper design with multiple layered samples with an indirect band gap. In this sense, the successful design of a transition-metal dichalcogenide-based device lies in finding an optimal way to freely control the film thickness and stacking order from a single sheet to multiple layered sheets.
Recently, an atmospheric-pressure chemical vapor deposition (APCVD) system was developed, enabling multi-stacked MoS2 crystals with all possible orientations between 0° and 60° to be obtained in a single set of experiments.11 In this process, the temperature was identified as a key parameter affecting the growth kinetics of the CVD-based MoS2 synthesis with a positive correlation between the growth rate and film thickness.9, 10, 11, 12, 13, 14 To date, stacking of up to three layers of MoS2 with various orientations has only been obtained by CVD at high temperatures (⩾850 °C).11, 12, 13, 14 In conventional CVD synthesis, high-order stacking is only possible at high temperatures. In contrast, in this research, our approach involves growing MoS2 stacked crystals with high stacking orders (AAA and ABA) at the lowest possible temperature. One way to achieve a lower growth temperature is the addition of alkali halides to MoO3.15 This addition of NaCl results in the formation of low sublimating Mo-oxychlorides, which in turn are responsible for the growth of highly stacked MoS2 crystals.
Stacking of MoS2 crystals can be categorized in three groups: (a) repeated-layer piling with the same orientation, as in AA(A…); (b) repeated-layer piling with alternating orientations, as in AB(AB…); and (c) a mixed-layer piling with false order in the abovementioned stacking orders, such as AAB… or AABB…11 Intensive scanning transmission electron microscopy analysis has proven the existence of an AA(A…)-type arrangement in 3R-phase crystals possessing broken inversion symmetry, whereas AB(A…)-type stacking can form a 2H-phase similar to that of natural crystals, where the net symmetry of the inversion depends whether there is an odd or even number of layers.10, 11, 12, 13, 16, 17 Moreover, the remaining stacking order, such as A(BB…) or AA(BA...), with a false order of either AB(A...) or AA(A...) gives rise to a combination of 2H and 3R-phases. Note that these stacking orientations tune the electronic properties by engineering interlayer distances and structural symmetry.3, 11, 13 In particular, the spin–orbit coupling (SOC) effect, valley polarization, and representative nonlinear optical properties, such as second-harmonic generation (SHG), are highly affected by the stacking configuration and subsequent structural symmetry.3, 4, 5, 11, 16, 17 To the best of our knowledge, few studies of stacking-orientation-controlled samples of more than three layers and subsequent characterization with PL and Raman spectroscopy have been conducted.10, 11, 12, 13, 18 Furthermore, studying the nonlinear optical properties, such as SHG or four-wave mixing (FWM), as a function of the layer number and stacking orientation of the multi-stacked crystals grown by CVD have scarcely been sought.4, 5, 6 The minute variations of the band structures according to the geometry and order of stacking are sufficient to modulate the nonlinear optical susceptibility, and hence, versatile MoS2 crystals synthesized by CVD play a crucial role in understanding fundamental optoelectronic properties.
In this report, we provide a synthetic modality of multi-stacked MoS2 crystals with different orientations and characterize their optical properties. More than 18 definable layer thicknesses are successfully synthesized using monolayer and bilayer MoS2 crystals as seeds layers. We further explore the PL, Raman, and absorption spectroscopies of various stacking-oriented samples and observe meaningful gradual spectroscopic evolutions induced by structural changes and interlayer interactions. The first-principles calculations are well consistent with the observed electronic band structures and reveal the excitonic emission. Additionally, the degree of the SOC effect in splitting the valence-band maxima at the K point is modulated by the stacking orientation. Additionally, the centers of symmetry, stacking orientations, and crystalline domains in a single specimen are more deeply assessed using FWM and SHG. The SHG signal of the AA(A…)-stacking crystal is drastically enhanced compared to the naturally occurring 2H-type AB(A…)-stacking and increases gradually with an increasing layer thickness. In contrast to AA(A…)-stacking, AB(A…)-stacking has the strongest SHG signal for a monolayer and then decreases gradually for an odd number of layers with no measurable signal for an even number of layers. Our approach of synthesizing high-quality multi-stacked MoS2 crystals and the associated background understanding provides a valuable direction for the future design of optoelectronic devices using diversely stacked few-layer MoS2 flakes.
Materials and methods
CVD synthesis of multi-stacked MoS2
The MoS2-stacked crystals were grown by APCVD in a two-zone furnace with a 2-inch diameter horizontal quartz tube. For growth, a 15 mg mixture of molybdenum oxide (MoO3) (⩾99.5%, Sigma-Aldrich, St Louis, MO, USA) and NaCl (⩾99.99%, Sigma-Aldrich) was loaded into a crucible located at the center of a high-temperature furnace. Sulfur (S) (0.8 g, ⩾99.5%, Sigma-Aldrich, St Louis, MO, USA) powder was placed in the upstream region 15 cm away from the center of the MoO3 zone. Before CVD growth, a 300-nm-thick SiO2/Si substrate was cleaned first in water followed by acetone and finally in isopropyl alcohol and then dried using N2. The Si/SiO2 wafer was placed on the top of the boat, facing the polished side downwards. The temperatures of the MoO3 and S zones were kept at 850 and 200 °C, respectively. Ar/H2 gas (50/7.5 sccm) was introduced as a carrier gas and to create a reducing atmosphere to promote the reaction. The S zone was preheated and moved when the MoO3 zone reached 250 °C. The furnace was heated with a ramp rate of 35 °C per min to the growth temperature and held there for 30 min. After the growth, the furnace was cooled naturally to room temperature.
Raman and PL characterization
The CVD-grown sample was characterized using PL and Raman spectroscopies (Horiba Jovin Yvon, LabRAM Aramis) atomic force microscopy (AFM) imaging (Park system, NX-10). The diameter of the illumination volume at the focus of the PL and Raman measurements was approximately 350 nm. Scattered light was collected through the objective used for illumination and guided to a 50-cm-long monochromator (equipped with a cooled CCD) through free space. Diffraction gratings with 600 and 1800 grooves mm−1 were used to collect the PL and Raman spectra, respectively. The 532-nm lines of a solid-state laser were used at intensities of less than 300 μW in a commercial confocal microscope system equipped with a 0.9-NA objective lens. With this power level of laser illumination, no physical damage or oxidation was expected to occur in the MoS2 film.
Computational details
The simulations were performed using density functional theory with the projector-augmented-wave method,19, 20 as implemented in the Vienna ab initio simulation package code.21 The Perdew–Burke–Ernzerhof22 generalized-gradient-approximation exchange-correlation functional was used, and an energy cutoff of 500 eV was used for the plane-wave expansion. In this calculation, an integration over the Brillouin zone was carried out using a 24 × 24 × 1 Monkhorst–Pack k-point mesh for all considered systems and a vacuum region accounting for more than 20 Å. All geometries were optimized using the conjugate-gradient method (force less than 0.0001 eV Å−1) with a van der Waals (vdW) correction (optB88-vdW functional)23, 24 on the interlayer distances. To obtain a more accurate electronic band structure over the conventional generalized-gradient-approximation functional, here, we used the computationally expensive Heyd–Scuseria–Ernzerhof (HSE06)25 hybrid functional with SOC.
Nonlinear optical characterization
A dual-mode erbium-doped fiber laser (Insight Deepsee Dual, Spectra-Physics, Santa Clara, CA, USA) was combined with a confocal microscope (Olympus, IX 83, Tokyo, Japan) to create multimodal (SHG and FWM) nonlinear optical images of the CVD-grown MoS2 flakes. The dual-mode laser housing emits a fundamental ultrafast (80-MHz) pulse train (1040 nm, FWHM ~220 fs), which synchronously pumps inside optical-parametric oscillators to generate a wavelength-variable (from 680 to 1300 nm) pulse train (FWHM 120 fs). The beam intensity was adjusted using a spiral-type neutral-density filter (Thorlabs, NDC-100C-4M, Newton, MA, USA). The time gap between two pulses was synchronized using a commercial translational stage (Sigma-Koki, SGSP46-500, Tokyo, Japan). Two spatially overlapped beams were directed using a dichroic mirror (Thorlabs, DMSP1000R, Newton, MA, USA) to the galvanometric x–y directional mirror controlled by a scanning system (Olympus, Fluoview 1000, Tokyo, Japan) to achieve real-time image acquisition. They were also monitored by a CCD camera (PIXIS 100B, Princeton Instruments, Trenton,NJ, USA) assisted by a monochromator (Acton SP2300, Princeton Instruments, Trenton, NJ, USA) for wide-wavelength spectroscopy (500~700 nm).
The details of the nonlinear optical microscopy setup have been reported previously26, 27. Briefly, we employed a fiber-optically amplified femtosecond laser (Insight Deepsee Dual, Spectra-Physics, Santa Clara, CA, USA) as an illumination source for the SHG and FWM imaging after being assembled on an inverted type microscope (Olympus, IX 83, Tokyo, Japan). We used a ~1 mW 800 nm beam (~120 fs) and a 1 mW 1040 nm beam (~220 fs) to generate the SHG at 520 nm and FWM at 650 nm, respectively. The beams were focused with a 1.35 NA UPlanFLN objective lens, and the produced SHG/FWM signals were collected by a photomultiplier tube (3523, Hamamatsu, Shizuoka, Japan) in reflection mode using two commercial filters (FF520/15, FF650/40, Semrock, Rochester, USA). The typical spatial resolution of the SHG microscope was ~300 nm.
Results and discussion
Synthesis of multi-stacked MoS2 crystals
Figure 1a describes the synthesis strategy based on the layer-by-layer growth of multi-stacked MoS2 crystals by the APCVD technique. Briefly, the APCVD system consists of two zones for sulfur (S) and MoO3+NaCl powders, respectively. The boat contains a 15-mg mixture of MoO3 and NaCl loaded in the center of a 2-inch-diameter horizontal quartz tube. The growth substrate (300-nm SiO2/Si) is placed ∼10 mm above the precursor (MoO3+NaCl) with the polished face upside down (Figure 1a). Another boat containing S powder (0.8 g) is positioned in the upstream region 15 cm away from the precursor. The experimental section provides more details concerning the synthesis process. Note that the deposition range of the MoS2 crystals on the growth substrate is sectioned into four parts from the center to the edge (Supplementary Figure S1).
Stacking-oriented CVD fabrication of MoS2 multiple-layer systems. (a) Schematic representation of the synthesis of multi-stacked MoS2 crystals via APCVD. (b) 2L–4L stacks of MoS2 crystals ‘seeded’ by monolayer systems. (c) 3L–7L stacks of MoS2 crystals seeded by bilayer systems. (d) Optical and AFM images for 10L and 18L stacked MoS2 crystals. All scale bars from (b) to (d) correspond to 5 μm. (e) Shape transformation of the MoS2 crystals from triangles to hexagons. Scale bar of (e) corresponds to 4 μm. CVD, chemical vapor deposition; MoS2, molybdenum disulfide; APCVD, atmospheric-pressure chemical vapor deposition.
Generally, highly stacked crystal growth without using NaCl is possible only at temperatures ⩾900 °C. With the aim of accelerating the reaction kinetics, we introduced NaCl as a growth promoter for the synthesis of multi-stacked MoS2 crystals. Mo-oxychlorides have a low sublimation temperature, owing to the fusion of NaCl and MoO3, followed by rapid vaporization, making it difficult to regulate the rate of the supply sources. This variable rate of evaporation leads to a very high precursor availability in the reaction zone, resulting in the formation of highly stacked MoS2 crystals with different stacking orientations. The uneven distribution of precursors from the center to the edge of the reaction zone helps in the formation of differently ordered highly stacked MoS2 crystals over the growth substrate (Supplementary Figure S1). Unlike the conventional MoO3 precursor with a high sublimation temperature of ~700 °C, herein, the primary growth precursors are MoO2Cl2 and MoOCl4 with sublimation temperatures of ~100 and ~156 °C, respectively. The following equations give the possible reaction route:


Solid MoO3 fuses with NaCl at 600 °C to form Na2MoO4, MoO2Cl2 and MoOCl4.28 Na2MoO4 is a solid and completely non-volatile product, whereas MoO2Cl2 and MoOCl4 are both volatile. These Na-containing intermediates, which are similar to PTAS (perylene-3,4,9,10-tetracarboxylic acid tetrapotassium salt) and PTCDA (perylene-3,4,9,10-tetracarboxylic dianhydride) seeds, provide nucleation sites on the substrate and then are sulfurized into the oxi-chalcogenide particles. In other words, these Na-intermediate compounds help reduce the energy of the reaction (energy required for the reactants to form the final product) required to form the final product (MoS2) by lowering the overall growth temperature. In the following step, the particles are converted into highly stacked MoS2 crystals with different stacking orientations by exposure to continuous sulfur vapor. At the same time, the addition of Na atoms enlarges the space between the sheets and enhances the separation process, resulting in a solid–vapor reaction. The amount of NaCl has a variable influence on nucleation and growth under given conditions. With an increase of the NaCl amount, multi-stacked crystal growth dominates instead of monolayer MoS2 domain growth, which is an indication of the rapid growth rate. Furthermore, the effect of NaCl becomes more prominent as the temperature increases, because the rate of the chemical reaction is directly proportional to the temperature. Compared to the reaction temperature used for the synthesis of highly stacked MoS2 crystals using the conventional method (⩾950 °C), the temperature applied in this work is dramatically reduced by the addition of the NaCl growth promoter (850 °C). In conclusion, by controlling the amounts of Mo precursor and NaCl at a particular temperature, the stacking order can be controlled. An XPS study was carried out for these stacked crystals, and it revealed no characteristic peaks for Na1s and Cl2p, suggesting that the stacked MoS2 crystals are free from contamination by alkali metals and halogen atoms17 (Supplementary Figures S4c and d). In addition, energy-dispersive spectroscopy analysis also shows the absence of any trace Na and Cl in the as-grown MoS2 crystals (Supplementary Table S1). The Mo metal in MoS2 has no available d-electrons to fill the dZ2 level, resulting in an exclusive octahedral Mo geometry to offer a more stable structure. The AB(A…)-stacking sequence has hexagonal close packing with a coordination number of 12 and packing efficiency of 74%, whereas AA(A…) stacking results in simple cubic packing with a coordination number of 6 and packing efficiency of 52%. Higher coordination numbers and packing efficiencies make AB(A…) stacking energetically more stable and preferred over AA(A…). Schematic representations of the 2H, 3R and mixed-type stacking orders for 2L and 3L are shown in Supplementary Figure S3.
The AB(A…)-stacked MoS2 crystals with the lowest formation energy are dominant among those grown by APCVD, indicating that our growth conditions favor this stacking over other high-energy stacking sequences (false stacking) because of the higher-energy barriers required by those configurations.11 Figure 1b shows the MoS2-monolayer seeded stacking crystals only up to 4L, as the precursor concentration gradient is the lowest in this area. Interestingly, in some isolated part of the substrate, star-shaped stacking was also observed, as shown in Supplementary Figure S2a. Upon moving toward the center, the precursor concentration gradient increases the chance of forming isolated MoS2-bilayer seeded multi-stacked crystals (multi-stacked crystals grown on an individual bilayer MoS2 unit) with stacking orders up to 7L (Figure 1c). Furthermore, when the precursor concentration gradient peaks near the summit point, multi-stacked MoS2 crystals with the highest stacking order are observed. Figure 1d illustrates the OM and AFM images of 10L and 18L multi-stacked MoS2 crystals with different orientations, together with the corresponding AFM height profiles.
In addition to the triangular shape, other shapes were also formed during the growth of the multi-stacked MoS2 crystals. By varying the Mo:S ratio, the shapes of the MoS2 crystals evolve from a triangle to a truncated triangle and finally become hexagonal29, 30, as shown in Figure 1e. The shape transformation process along the direction perpendicular to the carrier-gas flow stipulates that the Mo:S ratio change is the primary reason for the shape transformation. All conditions, including the growth temperature and S concentration, are constant in this direction, except for the different masses of Mo. Thus, the Mo:S ratio plays an important role and could be a determining parameter.
The confined Mo:S atomic ratio controls the final shape of the MoS2 crystals, as explained by the Wulff construction principle,29, 30 which states that specific crystal shapes are preferred over others depending on their surface energies. In other words, the surface energy and its dependence on the crystallographic orientation can define the equilibrium shape of a crystal. When the Mo:S atomic ratio matches the stoichiometric ratio of MoS2 (1:2) (here 0.51), Mo and S terminations follow the same growth rates. Thus, the dominant shape of the MoS2 crystals is hexagonal (Growth I). However, with Mo:S⩾1:2, a Mo-rich atmosphere results. Once the S-terminated edges grow rapidly and finally disappear, the entire crystal will possess Mo-terminated edges with a triangular shape (Growth II) (here; 0.45). However, when the Mo:S atomic ratio is between growths I and II (here; 0.48), the MoS2 crystal will transform into a truncated triangle.28, 31 Additional evidence supporting the above information is given by energy-dispersive spectroscopy analysis (Supplementary Table). Based on the APCVD system, multi-stacked MoS2 crystals can be formed not only in the shape of triangles but also in the shapes of truncated triangles and hexagons, as shown in Supplementary Figures 2b and c. We further describe the transformation of the MoS2 crystals from a monolayer to complete bilayer in Supplementary Figure S2d. This bilayer forms when the top layer entirely extends to the edges of the bottom layer. A low Mo-concentration gradient at the monolayer site causes a low stacking order (3–4L), whereas a very high Mo-concentration gradient near the center results in bilayer seeded highly stacked MoS2 crystals (⩾18 L).
In the APCVD system, a MoS2-stacking order change is possible along the X- (carrier-gas flow) and Y-axes (perpendicular to the gas flow) because of the change in the Mo-concentration gradient along both the axes. The precursor concentration gradient decreases toward the edge of the deposited substrate as the deposition site becomes farther from the precursor, resulting in a reduced stacking order. The thickness of the obtained crystals can be tuned from 1L to ⩾18L by controlling the amount of precursor and growth temperature. Moreover, the temperature for introducing sulfur is also a critical parameter for the well-defined layer-by-layer stacking of MoS2 with an ideal size and shape. The introduction of sulfur into the Mo precursor zone is a determining factor for the size of the MoS2 crystals. By controlling it, MoS2 crystals with sizes >100 μm can also be fabricated using APCVD growth. Here, the introduction of sulfur before the precursor zone reaches 150 °C results in the formation of bulk MoS2 that does not sublime under the given conditions but leads to no crystal growth on the substrate. In contrast, early introduction of sulfur leads to smaller crystals, and delayed introduction forms large-area bilayer seeded multi-stacked MoS2 crystals. In conclusion, this growth method of stacked MoS2 crystals with controlled orientation is scalable to large-size crystals. The growth temperature also governs the stacking order and pattern. Below 850 °C, the stacking order decreases with a high probability of monolayer-based stacked crystals covering isolated monolayer crystals in some areas. When the growth temperature increases above 850 °C, the stacking order increases, forming bilayer seeded crystals with some layers reaching up to ~15–20L with the formation of completely grown 3L or 4L AA(A…)- and AB(A…)-stacked MoS2 crystals.30 Furthermore, this growth is governed by a terrace-growth mechanism, wherein the triangles stack up layer by layer and shrink gradually to the center. During this growth process, the upper layers are formed later and have a shorter time to grow. Therefore, the lateral layer size decreases with an increasing height, and monolayer-by-monolayer-stacked MoS2 crystals are finally formed.29, 30, 31, 32, 33, 34
Stacking-oriented phonon frequencies in the Raman spectra
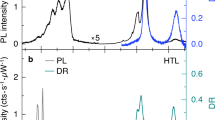
We critically examined the high-energy phonons in the Raman spectra of multi-stacked MoS2 crystals and exploited the stacking-induced structural changes and interlayer vdW interactions. As illustrated in Figure 2a, a MoS2 crystal consists of two well-defined, strong Raman bands attributed to lattice vibrations in two specific directions, which are denoted as in-plane (E2g1) and out-of-plane (A1g) vibrations.1, 2, 7, 8, 9, 10, 11, 12, 13, 35, 36, 37, 38, 39 Since the peak positions and frequency differences between E2g1 and A1g are known to reflect the spectroscopic figures induced by the shape and thickness variations of multi-stacked MoS2 crystals, we first compared the Raman spectra of the monolayer and bilayer hexagonal (dotted line) and triangular (solid line) crystals, as shown in Figure 2a. Both the hexagons and triangles exhibited well-defined A1g and E2g1 Raman modes. The peak positions of the A1g modes of both the monolayer crystals coincide, whereas the corresponding E2g1 mode of the hexagons was noticeably softened compared to that of the triangles. However, in the hexagonal bilayers, both the E2g1 and A1g modes softened by approximately 1.5 cm−1 compared to that of the triangular bilayers. Dislocation cores, vacancies or lattice mismatches are known to be highly capable of forming during crystal growth, resulting in subtle differences in the phonon frequencies of the Raman spectra. A recently reported result suggests that the presence of either an S or W vacancy is more likely to lower the Raman frequency in a hexagonal WS2 single crystal.36 In this manner, the relatively softened E2g1 vibrations in both hexagonal mono- and bilayer MoS2 likely result from an effect of vacancy induced defect states.
Shape- and stacking-orientation-dependent Raman spectroscopic characterization of the MoS2 crystals as a function of the layer thickness. (a) Raman spectra for various layer thicknesses and stacking orientations achieved using a 0.1-mW, 532-nm laser excitation source. All spectra were taken from a triangular-shaped sheet (solid lines), except for two hexagonal cases (dashed lines). Guiding arrows are inserted to show the trends of the peak changes among similar stacking orientation species. Both the E2g1 and A1g modes of the AA(A...)-type stacking configurations (red dashed line) are blueshifted compared to the AB(A...)-type stacking configurations (blue dashed line) for layer thicknesses greater than 2L. (b) Peak frequencies (right axis) of the E2g1 and A1g phonon vibrations and their peak-to-peak differences (left axis) are plotted as functions of the layer thickness. Note that both the E2g1 and A1g modes of the ‘fault-ordered’ AAB(A…)-type stacking configurations possess Raman frequencies (black balls) located between the AA(A…)- and AB(A…)-type stacking configurations.
We also studied the Raman spectral changes of triangular MoS2 crystals with regards to various stacking orientations and thicknesses ranging from 1L to 6L. Raman spectra with distinct shifts in the A1g and E2g1 modes are demonstrated in Figure 2a. The layer-thickness-/orientation-dependent variations of the E2g1 and A1g vibrational modes are summarized in Figure 2b. Blue and red dashed lines indicated the trends of the Raman frequencies for the AB(A…)- and AA(A…)-stacking configurations, respectively. Here, the Raman peak positions of the mixed orientations are located in between the AA(A…)- and AB(A…)-stacking configurations, as indicated by the isolated balls (E2g1) or circles (A1g) in Figure 2b.
The thickness-dependent shifting of the Raman spectra for the AB(A…) vdW-layer system manifests the similarity of the developed interlayer coupling behavior of the exfoliated natural crystals.1, 2, 35 As we observed, the A1g mode blueshifted (stiffened), the E2g1 mode redshifted (softened), and the separations between the E2g1 and A1g modes gradually increased with an increasing layer thickness. The blueshift of the A1g mode with an increasing layer number indicates stronger interlayer vdW interactions, whereas the redshift of the E2g1 mode arises from dielectric-screening-related long-range Coulomb interactions.1, 2, 35 In contrast, both the A1g and E2g1 Raman modes of the AA(A…)-stacked samples with more than two layers are stiffened compared to those of the AB(A…)-stacked crystals. We note that the peak frequency differences between the two modes for AA(A…)-type and AB(A…)-type stacking are similar, suggesting nearly equal shifting of the E2g1 and A1g frequency modes, as marked as red and blue dashed lines, respectively (Figure 2b). The shifting tendency of the phonon frequencies depending on the stacking orientations is consistent with the previously calculated result at the gamma point.11 More details concerning the stacking-order dependence of the Raman peak positions for each MoS2 crystal (2L–5L) can be found in Supplementary Figure S5. This interesting result reveals that a reduction in the interlayer distances occurs in the AA(A…)-stacked crystals compared to the AB(A…)-stacked crystals, which is similar to a previously reported result.11 An experimental study carried out by Yan et al.11 demonstrated that the E2g1 mode for the AAA-trilayer was barely blueshifted, while the frequency of the A1g mode was stiffened with respect to the ABA-trilayer. The E2g1 mode preservation against layer stacking in the AAA-type crystal, as reported in Yan et al.11 might be related to the structural diversity induced by the fabrication method, as Raman spectroscopy of the CVD crystal is highly sensitive to the growth conditions and quality of the sample. We believe that our observation of considerable phonon stiffening for both the E2g1 and A1g modes in the AA(A…)-stacked crystals becomes visible due to the negligible contributions of CVD-induced structural defects.
Stacking-oriented excitonic behavior in the PL spectra
To understand the excitonic behavior of the various stacking-oriented layers with different geometries, we compared the PL emission spectra of the hexagonal and triangular MoS2 crystals, as shown in Figure 3a. The PL mapping images show that the hexagonal crystals has non-uniform and edge-prevailing PL, while the triangular crystal has uniform PL from the center-to-edge regions. A lower PL intensity in the inner region of the hexagonal sample is mainly ascribed to the influence of defect states localized in the inner region. As illustrated by a recent study regarding a hexagonal WS2 monolayer, defect states can be a key factor in reducing the PL emission in a localized fashion.36 Moreover, the tailored PL intensity is also related to the band structure change via an extra-strain effect induced by merged defects.37 The broadened and redshifted PL spectrum of the hexagonal monolayer compared to that of the triangular monolayer indicates the possible involvement of defect-assisted quenching in the PL emission.36 In fact, the activity of those defect states can be diminished using a nonoxidizing organic superacid, such as bis(trifluoromethane)sulfonimide, providing a drastic enhancement of the PL emission.40, 41 Thus, to reaffirm that the decreased PL intensity in our hexagonal crystal originates from defects, we dipped the samples in a bis(trifluoromethane)sulfonimide solution for 1 h and found that the PL emissions drastically recovered in both the triangles and hexagons. The degree of enhancement was more severe in the hexagon than the triangle, implying that more defect states initially existed in the hexagonal MoS2 crystals. The corresponding results are provided in Supplementary Figure S6.
Effects of the shape and stacking orientation on the electronic band structures of multilayer MoS2 crystals. (a) Optical and photoluminescence (PL) mapping images of the flakes containing 1L, 2L-AA and 2L-AB triangular- and hexagonal-shaped crystals are shown at the top (scale bar is 3 μm). All spectra and mappings are acquired using 532-nm-laser illumination. The PL intensity of the triangular pit was higher than those of the hexagonal crystals. The shape- and stacking-orientation-dependent PL spectra are shown at the bottom panel as a function of the layer thickness. The positional variations of the A and B peaks are guided by black dashed lines for the hexagons and triangles, which were roughly described with an increasing thickness from 1L to 6L. (b) The positional variations in the A peak (right) and integrated PL intensities (left) were dependent on the layer thickness and stacking orientation configuration. The monolayer triangular crystal demonstrated the highest PL intensity due to its direct band gap. The red and blue dashed lines guide the intensity variations of the AAA... and ABA... stacking cases, respectively. (c) Valence-band splitting (VBS) of the variously stacked crystals plotted as a function of the number of layers. (d) Absorption spectra obtained from the 1L, 2L-AA, 2L-AB, 3L-ABA and 3L-AAA flakes with the A, B and C excitons clearly resolved. (e) Calculated band structures of the ABAB- (left panel) and AAAA-stacked (right panel) 4L-MoS2 systems. The VBS near the K point is magnified to better show the direct-band-gap transitions. The estimated error bar is provided in the corresponding graph with a pink color.
We further characterized the PL emission spectra from 1L to 6 L for various stacking configurations (Figure 3a, bottom panel). The monolayer exhibited the strongest PL intensity as a result of the vertical quantum-confinement effect induced by the indirect-to-direct band-gap crossover in a single-layer limit.1, 2, 3 For the multilayer systems, each thick crystal also exhibited stacking-orientation-dependent PL behaviors. The maximum PL intensity was observed for the AA(A…)-type stacking, followed by the mixed-type stacking, and the minimum PL was observed in the AB(A…)-type stacked crystals. Simultaneously taking PL images of 2L-AA and 2L-AB shown in the top panel of Figure 3a clearly exhibited the improved PL emission from the AA-stacked crystal. The variations of the peak positions and integrated PL intensities as a function of the layer number are displayed in Figure 3b. The related PL intensities gradually decreased from 1L to 6 L. The excitonic position, that is, the direct optical band gap, was unchanged among the stacking orientations but monotonically decreased from 1L to 3 L in a manner similar to those observed in previous studies.1, 2, 10, 11, 12, 13 Interestingly, for the AA(A…)-stacking configuration for greater than 4L, the optical band gap was slightly increased (by ~5–10 meV) compared to those of the other stacking orders. Detailed comparisons between the band gaps and integrated PL intensities from the 2L to 5 L crystals are summarized with regards to the different stacking orders in Supplementary Figure S7. Furthermore, we studied the PL and peak positional change of the indirect bands in the AA (3R)- and AB (2H)-stacked bilayer crystals. The indirect band gaps in both cases were very similar, except for being slightly broadened for the AA bilayer (Supplementary Figure S8). The observed PL spectra for the indirect band gaps of the CVD-grown AA and AB bilayers indicate the interlayer electronic coupling strength, while the slightly broadened bandwidth of AA suggests stronger interlayer coupling.12, 42
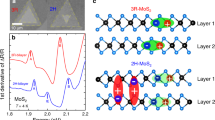
Next, the valence-band splitting (VBS) of the MoS2 crystals was studied as a function of the layer-number thickness and stacking-order configuration. Essentially, the amount of VBS was measured as the distance between the A- and B-peak energies observed in the PL or absorption spectra. Figure 3c shows the VBS tendencies from the 1L to 6 L crystals for different orientations measured from the PL spectra. The gradual increase in the VBS with an increasing layer thickness is in good agreement with previous results.1, 2 First, for 1L MoS2, SOC contributes to the VBS because the 1L crystal lattice has broken inversion symmetry. On the other hand, there is an even–odd variation in the structural symmetry of the AB(A…)-stacked multilayer: broken inversion symmetry is present (absent) in films with an odd (even) number of layers. Therefore, the major contribution to VBS is SOC for an odd number of layers, while for an even number of layer, the dominant effect is interlayer interactions.1, 2, 3, 16, 17 However, the structural symmetry in the AA(A…)-stacked multilayers is independent of the even–odd oscillation with the number of layers: all the layers should have broken inversion symmetry,10, 11, 12, 13 and thus, the observed VBS is mainly contributed by SOC. As shown in Figure 3c, the VBS phenomena exhibited a stacking-orientation dependence, with the AB(A…)-stacked crystal showing larger VBS than the AA(A…)-stacked crystal. This unique result under AA(A...)-stacking is observed as a result of the stacking-order-dependent shifting of the A and B excitonic PL peak positions. The A-peak position did not vary much until 4L and then slightly increased for AA(A...)-stacking. Meanwhile, the B peak gradually redshifted for AA(A...)-stacking, leading to reduced VBS as the layer thickness increased. The stacking-orientation-dependent A- and B-peak positions and their differences for 2L–5L are provided in Supplementary Figure S7. Further discussion on the nature of the splitting will be provided later in combination with the density functional theory calculation results.
A similar VBS trend was also observed in the differential-reflectance spectra (Figure 3d). We performed differential-reflectance measurements for the 1L, 2L-AA, 2L-AB, 3L-ABA and 3L-AAA stacking crystals after loading these crystals onto a transparent glass substrate. Reflection spectra of thin films measured from a transparent medium can be well interpreted as absorption spectra.1, 2 The energy gaps observed in the PL spectra are highly sensitive to small changes associated with the doping level or defect states in the absorption bands and can capture the sources of inaccuracies in band-gap estimations.1, 2, 41 In addition, absorption spectra allow the evolution of the electronic band structures in a broad energy range, including high-energy excitons. As illustrated, the absorption bands for the 1L, 2L-AA, 2L-AB, 3L-ABA and 3L-AAA stacking crystals clearly show A, B and C excitons (Figure 3d). The A and B peaks are lower-energy excitons created by the splitting of the topmost valence bands. On the other hand, the C peak located at the high-energy state is induced by the electronic transition from band nesting.8 The overall features of the absorption spectra taken from the 1L, AB bilayer and ABA-trilayer samples replicate the results observed in the literature.1, 2, 8 However, for the 2L-AA and 3L-AAA stacking orders, different VBS natures and peak positions of the related excitons emerge. The relatively smaller VBS of the AA(A…)-stacking than that of the AB(A…)-stacking observed in the PL study is also consistently observed in the absorption study. Notably, the optical band gap represented by the A-peak position remains unchanged for both the AA(A…) and AB(A…)-stackings, clearly complying with the weak direct band-gap changes originating from the stacking orientations, as suggested by the PL studies.3, 11, 12, 42 In contrast, the B-peak positions of the AA and AAA stackings have softened by approximately 20 meV, and thus, the VBS values in the AA(A…)-stacked bi- and trilayers are reduced compared to those in the AB(A…) bi- and trilayers. In addition, as shown in Figure 3d, the C peak barely changes with the stacking orientation. The gap of the AA(A…)-stacked bi- or trilayers is approximately 5~10 meV wider than that of the corresponding AB(A…)-stacked bi- or trilayers. We believe that this tendency of VBS and electronic band structure will be maintained in thicker AA(A…)- and AB(A…)-stacked crystals as well.
Stacking-oriented excitonic effects and valence-band splitting revealed by theoretical calculations
To understand the dependence of the electronic structure on the stacking orientation, we performed density functional theory calculations of the 3L and 4 L crystals with AA(A…)- and AB(A…)-stacking (Figure 3e). We used both the HSE06 and Perdew–Burke–Ernzerhof functionals including SOC and investigated the electronic band structures. Details of the theoretical results are provided in the Supplementary Information (Supplementary Figures S9–S11). As indicated in Figure 3e, the valence- and conduction-band edges of the 4L-AAAA-stacking crystal are relatively higher than those in the 4L-ABAB crystal and shifted by the same amount (~250 meV). Hence, any change in the net direct band gap value is compensated. Consequently, the band gaps remained constant in both cases. This up-shifting of the corresponding valence and conduction bands is also applicable for the 3L-AAA crystal, as shown in Supplementary Information (Supplementary Figures S9 and S11). Therefore, we concluded that the direct band gap is independent of the stacking orientation. However, the indirect band gap seems to change slightly between the AA(A…)- and AB(A…)-stacking orientations. For AB(A…)-stacking, MoS2 possesses an indirect band gap via ⋀–Γ, as indicated by the calculation result. This situation is modified for AA(A…)-stacking, where the conduction-band valley at the K point is aligned with a lower energy than the ⋀-valley by approximately 20 meV. We conjectured that C-exciton-gap widening, as observed in the absorption spectra of the AA bilayer, may also result from the relative motion between the conduction-band valleys at the K and ⋀ points. This modification between the conduction-band valleys likely causes the broadening of the indirect band gap, which can be realized with interlayer electronic coupling.3, 12, 42 Additionally, the different alignments between the two conduction bands at the K and ⋀ points also affect the relaxation process at the K point, leading to an improved direct PL emission for AA(A...)-stacking compared to AB(A...)-stacking.
Furthermore, the theoretical results based on the HSE and Perdew–Burke–Ernzerhof approximations agree well with the observed VBS observations. The splitting nature at the K point is magnified for the 4L-ABAB and 4L-AAAA crystals and is presented in Figure 3e, while related results for 3L are presented in the Supplementary Information (Supplementary Figures S9–S11). As expected, for AB(A...)-stacking, the splitting was mainly due to interlayer interactions for an even number of layers, while additional SOC modulated the splitting nature for an odd number of layers.15, 16 On the other hand, for AA(A...)-stacking, the valence-band states at the K point split into many sub-bands irrespective of the number of layers. The separation between any two sub-bands is uniform and theoretically estimated as 20 meV for AA(A...)-stacking, as this stacking remains in the 3R-phase, which does not have a symmetry-inversion center. As a result, SOC becomes dominant. As demonstrated, the splitting is more clearly resolved in the AA(A...)-stacked crystals than in the AB(A...)-stacked odd layers; however, the inversion symmetry is also broken for the latter. Here, more clearly resolved energy states at the K point of the valence-band maxima for all thicknesses of AA(A...)-stacked layers can be understood as strongly spin-polarized states.11, 43
Experimentally, we cannot resolve each of the spin-polarized states in the PL or absorption spectra, and instead, their average effect must be determined. As previously explained, from the PL and absorption spectra, we observed a smaller gap between two separated VBSs at a K point for AA(A...)-stacking than for AB(A...)-stacking. This result is caused by the vertical dispersion of the topmost valence bands representing the A and B transitions due to strongly polarized spin states. In addition, we note that vertical dispersion of the sub-energy states in the AA(A...)-stacking due to SOC also slightly influences the direct band gap position. The very small band-gap increment (~5–10 meV) beyond 4L for AA(A...)-stacking compared to AB(A...)-stacking reveals the effect of the spin-polarization-induced vertical dispersion of the valence-band edges. It is not surprising that dispersion is more effective for relatively thicker layers because a larger number of sub-bands are induced as a result of splitting. Moreover, we emphasize that our valence-band splitting result is obtained due to the completely polarized spin states in the AA(A...)-stacking, which is similar to the previously measured valley and spin polarizations of 3R-phase MoS2.3, 11, 43 Additionally, 3R-like MoS2 crystals, similar to AA(A...)-stacking, were also accompanied by a suppressed interlayer hopping effect.11 All these results indicate that the AA(A...)-stacked crystals of all layer thicknesses exhibited strongly spin-polarized valence-band states.
Stacking-oriented FWM and SHG microscopy
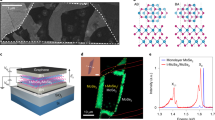
The structures and orientations of the monolayer to few-layer crystals with different stacking configurations were fully examined through FWM-correlated SHG microscopy. A schematic diagram illustrating the interaction of the pump-probe beam used to emit the nonlinear optical SHG and FWM signals is shown in Figure 4a. The spectral evolutions of SHG (520 nm) and FWM (652 nm) by two excitation beams (800 and 1040 nm) are given in Figure 4b, where the power dependences of both signals in the inset graphs also suggest that SHG and FWM are second- and third-order nonlinear signals, respectively. Pump and Stokes beams of approximately 1 and 8 mW, respectively, were utilized at the sample for all the SHG/FWM imaging in this work. In principle, the SHG from MoS2 is intense, as the crystalline structure of MoS2 belongs to the non-centrosymmetric point group D3h.3, 4, 5 If the input laser and output SHG signal have the same polarization parallel to the monolayer surface, the SHG output is proportional to |χbbb(2)|2 cos23φ, where χbbb(2) is the nonlinear-susceptibility element of MoS2, ‘b’ represents the crystalline axis along the mirror plane, and φ is the angle of the beam polarization away from the b-axis.
Thickness-dependent FWM and SHG imaging of multilayer MoS2 crystals. (a) A schematic diagram illustrating the interactions between the pump-probe (800, 1040 nm) laser beams and a stacking-oriented MoS2 atomic-crystal structure, generating second-order SHG and third-order FWM nonlinear optical signals. (b) The spectral evolutions of SHG (~520 nm) and FWM (~652 nm) by two excitation beams, together with their laser-power dependencies to assess the nonlinear susceptibilities. (c) Polarization-dependent SHG studies for 1L, 2L-AA and 2L-AB MoS2 (scale bars are 5 μm). (d) The FWM images correlated with the SHG images for different stacking configurations (top panel); the graphs in the bottom panel show the maximum intensity of the SHG for each layer with different stacking orientations, of which the maximum intensity positions were confirmed by rotating the crystal. The inset represents the zoomed SHG intensity variation trend of the ABA…-stacking configuration. The FWM signals from the corresponding crystals (pink ball) are plotted simultaneously (all scale bars are 2 μm). The estimated error bar is provided in the corresponding graph with a green color. The olive color plot represents the results of the model to explain the SH intensity of the AA(A...)-stacking crystals. FWM, four-wave mixing; SHG, second-harmonic signal.
We first studied the rotational behaviors of the 1L, 2L-AA and 2L-AB crystals, as shown in the polar plot (Figure 4c). The rotational behaviors of 1L and 2L-AA were studied from each thickness layer located in the same sample, and the 2L-AB sample was studied in another sample with a different crystal orientation. The incident lasers were linearly polarized and used to excite the samples with the analyzer angle set parallel to the incident beams. All the panoramic SHG images taken with regards to different angles are also provided in Supplementary Figure S12. The six-fold symmetry of the SHG signal with respect to sample rotation was well observed from the respective layers with petals lying along the perpendicular bisectors of each flake, analogous to previously results reported for the 2H crystal.3, 4 We note that the 1L, 2L-AA and 3L-AAA crystals demonstrated increased SH intensity with an increasing thickness due to the cumulative nature of the broken inversion symmetry, whereas the 2L-AB crystal showed feeble SH intensity due to the restored inversion symmetry. Polarization-dependent SHG intensities of the AAA and AAAB stackings are illustrated in Supplementary Figure S12. We estimated the polarization anisotropy {(Imax − Imin)/(Imax + 2Imin)} as the degree of SH polarizability for each sample, where Imax and Imin represent the maximum and minimum SH intensities for the sample rotation, respectively. For the crystals with non-centrosymmetric space groups, that is, 1L, 2L-AA and 3L-AAA, the polarization anisotropies were estimated as 70%, 80%, and 95%, respectively; this quantity was 10% for the centrosymmetric 2H-AB bilayer. The observed polarization anisotropies of 1L and 2L-AB are consistent with the result of the exfoliated sample (Supplementary Figure S13). The 10% level of remnant SH-polarization anisotropy in the AB bilayer was assumed to originate from stacking imperfection or substrate-induced imperfection. In contrast, the stronger polarization anisotropies of the AA and AAA crystals are presumably related to physical additions of SH-generating sources above the monolayers and the increased intensity differences between Imax and Imin.
Figure 4d presents a simultaneous monitoring of FWM and SHG for the different stacking configurations. The double-sided arrow indicates the directions of the two (pump and Stokes) parallel excited-beam polarizations. We compared the maximum intensity of the SHG for each layer, of which the position was determined by rotating the crystal. An arbitrary region simultaneously containing various thick crystals with multiple orientation configurations was fully traced via SHG imaging with respect to the sample rotation in Supplementary Figure S14. The FWM signals increased almost linearly with an increasing layer thickness, as previously reported in the literature, while the correlated SHG signal varied according to the stacking configuration.6 The 2H-like even-numbered layers with AB(A...)-stacking showed little SHG intensity due to the existence of inversion symmetry and followed the trend indicated by the blue dashed line. The 3R or AA(A...)-type stacked multilayer crystals presented intense SHG intensities and followed the trend of the red dashed line. Multilayer crystals with mixed stacking orders displayed SHG intensities located between the 2H and 3R-phases (black stars) depending on the deviation from the stacking orientations of the red/blue dashed lines. Note that all the image correlations between FWM and SHG and their correspondences to the graphs with different stacking orientations are illustrated in the top panel of Figure 4d, where the AA-type bilayer, in contrast to the Bernal-stacked bilayer (AB-type), demonstrates an SH intensity approximately four times higher than that of 1L. Similarly, the 3L, 4L and 5L AA(A...)-stacked crystals showed drastically enhanced SH intensities similar to the previously reported results from Zhao et al.44 These authors observed a nearly quadratic dependence of the SH intensity with the layer numbers in a set of exfoliated 3R-like crystals.44 To understand our intensity variation with varying layer numbers, we postulate a model based on the electric dipole approximation, which depends on the quadratic variation of the layer numbers in the AA(A...)-stacked crystals. The olive color plot in Figure 4d represents the quadratic model, which varies as a function of the layer number. The quadratic model well fits the experimental data and reveals the parallel alignment of the induced dipole in the AA(A...)-stacked crystals contributed strongly to the enhanced SH intensity. A more detailed description of the model is provided in Supplementary Figures S15 and S16. Additionally, more examples of FWM-correlated SHG images from triangularly shaped crystals with various thicknesses and multiple stacking orders are provided in Figure 5a and Supplementary Figure S17. In general, few stacking-oriented signatures are unequivocally identifiable through Raman or PL spectroscopy, except in rigorous studies with TEM or STEM modalities. Here, we found that either AB- or AA-type additions to the bilayer triangles were clearly viewable in the SHG-based image comparison, yet scarcely distinguishable using the optical- or FWM-imaging techniques. For example, the SHG signals from two adjacent bilayer crystals are distinctly shown in Figure 5b, indicating the different natures of the inversion symmetry breakage between two bilayers allegedly having FWM intensities with similar levels.
Shape- and stacking-orientation-dependent FWM and SHG imaging of multilayer MoS2 crystals. (a) Various types of layer stackings, starting either from monolayer or bilayer MoS2 crystals, resolved by collaborative FWM and SHG imaging. (b) Intensity comparison of the FWM and SHG images from two adjacent twin bilayer crystals having AA- and AB-stacking orientations. The AA-type stacked bilayer shows intense SHG compared to the AB-type bilayer, whereas the FWM images are identical regardless of the stacking order. (c) The optical, FWM and SHG images for differently shaped single-crystalline and polycrystalline MoS2 systems. Scale bars correspond to 2 μm. FWM, four-wave mixing; SHG, second-harmonic signal; MoS2, molybdenum disulfide.
Additionally, a simultaneous FWM and SHG imaging strategy was applied to investigate the various shapes of the CVD-grown MoS2 crystals. Figure 5c displays the shape-dependent FWM images in the top panel and the corresponding SHG images in the bottom panel. As the first two columns vividly suggest, the perfect hexagonal-shaped monolayer gave a homogeneous SHG contrast generated by the single crystal, whereas the ‘domains’ of the imperfect hexagonal or polygonal samples were selectively visualized by SHG. In other words, neither FWM nor optical images (top panel) could discriminate meaningful contrast from either the single or polycrystalline monolayer, while the SHG images successfully resolved the polycrystalline domain within a flake specimen created by the azimuthal-angle dependence of the SHG signal with respect to the incident light polarization. An extended view of the region simultaneously containing poly- and single-crystalline flakes is presented in Supplementary Figure S14.
Moreover, all the triangles stacked on the 1L-hexagonal crystal showed enhanced SHG irrespective of their stacking orientations, as illustrated in Supplementary Figure S18b. The SHG intensity ratio between the 1L-hexagon and hexagon/triangle bilayer was almost identical to that between the 1L-triangle and triangle/triangle bilayer. It is possible that the stacking orientation between two heterogeneously shaped crystals favors a staggered-lattice structure between the layers. A hexagonal bilayer is formed as a 2H-like phase with an inversion symmetry center, as indicated by the lack of SHG contrast. Interestingly, we can also visualize a star-shaped crystal via not only the thickness using FWM but also the stacking orientation using SHG; this crystal is clearly distinct from previously reported results that mentioned only polycrystalline star-shaped monolayers.4 Here, a single-crystalline star-shaped crystal with six arms was observable, where added layers were grown in the central region. The region of the black SHG contrast inside the 1L-star-shaped flake was created by the reversely oriented growth of the second layer. The bright central SH emission was allowed by the addition of more layers with stacking orientations identical to that of the first layer, where stacked layers in the star-shaped crystal could also be identified in the optical and FWM images. We believe that our raster-scanning SHG technique is helpful to quickly resolve the polarization-induced phase contrasts of various multilayered 2D-transition-metal dichalcogenide films, thereby providing a new way to design optically triggered CVD-based 2D optoelectronics.
In summary, we developed a method to synthesize multilayer MoS2 crystals with different stacking orientations by APCVD using NaCl as a growth promoter. NaCl was found to play a vital role in the formation of Mo-containing nucleation sites at a lower temperature, and Na ions helped weaken the interlayer adhesion, contributing to an increase in the growth rate for highly stacked MoS2 crystals with different orientations. The growth temperature dependence upon the stacking order and shape of multi-stacked crystals was studied. We revealed the stacking-orientation dependence of the crystal symmetry, phase, and associated electron–phonon coupling in the electronic band structure using optical investigations based on Raman spectroscopy, PL spectroscopy and a nonlinear technique of FWM-correlated SHG imaging. The Raman frequencies induced by the AA(A...)-stacking orientation clearly stiffened the E2g1 and A1g phonon vibrations for layer thicknesses greater than 3L as compared to those induced by the AB(A...)-stacking configuration, indicating enhanced interlayer interactions. The stacking dependence of the phonon vibrations can be used as a robust and convenient means of diagnosing interlayer interactions and structural changes. The experimental and theoretical study based on excitonic properties suggests that the stacking orientation is the key to engineering a fundamental band structure and improved PL emission in multilayer crystals with AA(A...) configurations. Moreover, highly spin-polarized states were observed in AA(A...)-stacked crystals of all thicknesses, in contrast to naturally stacked AB(A...) crystals, in which only odd numbers of multilayers exhibited spin polarization. Furthermore, the nonlinear FWM-correlated SHG-image-based study showed that the AA(A...)-stacked-multilayer MoS2 exhibited stronger SH intensities for crystals of all thicknesses than those of AB(A...)-stacked crystals, thereby confirming that the broken structural symmetry in AA(A...)-stacked-multilayer MoS2 manifested stronger SOC-induced band splitting, as supported by first-principles calculations. FWM is stacking-orientation independent and exhibited a linear dependence on the layer thickness. We carefully inspected the FWM and SHG intensities and confirmed the structural symmetry by detecting an optically invisible stacking orientation in a multi-stacked CVD crystal with 2H and 3R phases in the Brillouin zone. Our study based on crystals with different shapes and stacking configurations provides a new avenue for developing future optoelectronic devices.
References
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Dhakal, K. P., Duong, D. L., Lee, J., Nam, H., Kim, M., Kan, M., Lee, Y. H. & Kim, J. Confocal absorption spectral imaging of MoS2: optical transitions depending on the atomic thickness of intrinsic and chemically doped MoS2 . Nanoscale 6, 13028–13035 (2014).
Jiang, T., Liu, H., Huang, D., Zhang, S., Li, Y., Gong, X., Shen, Y. R., Liu, W. T. & Wu, S. Valley and band structure engineering of folded MoS2 bilayers. Nat. Nanotechnol. 9, 825–829 (2014).
Hsu, W. T., Zhao, Z. A., Li, L. J., Chen, C. H., Chiu, M. H., Chang, P. S., Chou, Y.C. & Chang, W.H. Second harmonic generation from artificially stacked transition metal dichalcogenide twisted bilayers. ACS Nano 8, 2951–2958 (2014).
Li, Y., Rao, Y., Mak, K. F., You, Y., Wang, S., Dean, C. R. & Heinz, T. F. Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation. Nano Lett. 13, 3329–3333 (2013).
Li, D., Xiong, W., Jiang, L., Xiao, Z., Golgir, H. R., Wang, M., Huang, X., Zhou, Y., Lin, Z., Song, J., Ducharme, S., Jiang, L., Silvain, J. F. & Lu, Y. Multimodal nonlinear optical imaging of MoS2 and MoS2-based van der Waals heterostructures. ACS Nano 10, 3766–3775 (2016).
Park, S., Kim, M. S., Kim, H., Lee, J., Han, G. H., Jung, J. & Kim, J. Spectroscopic visualization of grain boundaries of monolayer molybdenum disulfide by stacking bilayers. ACS Nano 9, 11042–11048 (2015).
Kozawa, D., Kumar, R., Carvalho, A., Kumar Amara, K., Zhao, W., Wang, S., Toh, M., Ribeiro, R. M., Castro Neto, A. H., Matsuda, K. & Eda, G. Photocarrier relaxation pathway in two-dimensional semiconducting transition metal dichalcogenides. Nat. Commun. 5, 1–7 (2014).
Chen, X., Park, Y. J., Das, T., Jang, H., Lee, J. B. & Ahn, J. H. Lithography-free plasma-induced patterned growth of MoS2 and its heterojunction with graphene. Nanoscale 8, 15181–15188 (2016).
Zheng, J., Yan, X., Lu, Z., Qiu, H., Xu, G., Zhou, X., Wang, P., Pan, X., Liu, K. & Jiao, L. High-mobility multilayered MoS2 flakes with low contact resistance grown by chemical vapor deposition. Adv. Mater. 29, 1604540 (2017).
Yan, J., Xia, J., Wang, X., Liu, L., Kuo, J. L., Tay, B. K., Chen, S., Zhou, W., Liu, Z. & Shen, Z. X. Stacking-dependent interlayer coupling in trilayer MoS2 with broken inversion symmetry. Nano Lett. 15, 8155–8161 (2015).
Xia, M., Li, B., Yin, K., Capellini, G., Niu, G., Gong, Y., Zhou, W., Ajayan, P. M. & Xie, Y. H. Spectroscopic signatures of AA’ and AB stacking of chemical vapor deposited bilayer MoS2 . ACS Nano 9, 12246–12254 (2015).
Yan, A., Chen, W., Ophus, C., Ciston, J., Lin, Y., Persson, K. & Zettl, A. Identifying different stacking sequences in few-layer CVD-grown MoS2 by low-energy atomic-resolution scanning transmission electron microscopy. Phys. Rev. B 93, 041420 (2016).
Gong, Y., Ye, G., Lei, S., Shi, G., He, Y., Lin, J., Zhang, X., Vajtai, R., Pantelides, S. T. & Zhou, W. Synthesis of millimeter-scale transition metal dichalcogenides single crystals. Adv. Funct. Mater. 26, 2009–2015 (2016).
Li, S., Wang, S., Tang, D. M., Zhao, W., Xu, H., Chu, L., Bando, Y., Golberg, D. & Eda, G. Halide-assisted atmospheric pressure growth of large WSe2 and WS2 monolayer crystals. Appl. Mater. Today 1, 60–66 (2015).
Latzke, D. W., Zhang, W., Suslu, A., Chang, T. R., Lin, H., Jeng, H. T., Tongay, S., Wu, J., Bansil, A. & Lanzara, A. Electronic structure, spin-orbit coupling, and interlayer interaction in bulk MoS2 and WS2 . Phys. Rev. B 91, 235202 (2015).
Jin, W., Yeh, P. C., Zaki, N., Zhang, D., Sadowski, J. T., Al-Mahboob, A., van der Zande, A. M., Chenet, D. A., Dadap, J. I., Herman, I. P., Sutter, P., Hone, J. & Osgood, R. M. Jr. Direct measurement of the thickness-dependent electronic band structure of MoS2 using angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 111, 106801 (2013).
Lee, J-U., Kim, K., Han, S., Ryu, G. H., Lee, Z. & Cheong, H. Raman signatures of polytypism in molybdenum disulfide. ACS Nano 10, 1948 (2016).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Klimeš, J., Bowler, D. R. & Michaelides, A. Chemical accuracy for the Van der Waals density functional. J. Phys. Condens. Matter. 22, 022201 (2010).
Klimeš, J., Bowler, D. R. & Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131 (2011).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Lee, D., Jeong, D.-E., Son, H. G., Yamaoka, Y., Kim, H., Seo, K., Khan, A. A., Roh, T.-Y., Moon, D. W., Lee, Y. & Lee, S.-J.V. SREBP and MDT-15 protect C. elegans from glucose-induced accelerated aging by preventing accumulation of saturated fat. Genes & Dev 29, 2490–2503 (2015).
Kim, H., Kim, D.-Y., Joo, K.-I., Kim, J.-H., Jeong, S.M., Lee, E. S., Hahm, J.-H., Kim, K. & Moon, D.W. Coherent Raman imaging of live muscle sarcomeres assisted by SFG microscopy. Sci. Rep. 7, 9211 (2017).
Johnson, D. A., Levy, J. H., Taylor, J. C., Waugh, A. B. & Brough, J. Purification of molybdenum: volatilisation processes using MoO3 . Polyhedron 1, 479–482 (1982).
Wang, S., Rong, Y., Fan, Y., Pacios, M., Bhaskaran, H., He, K. & Warner, J. H. Shape evolution of monolayer MoS2 crystals grown by chemical vapor deposition. Chem. Mater. 26, 6371–6379 (2014).
Li, S. F., Zhao, X. J., Xu, X. S., Gao, Y. & Zhang, Z.Y. Stacking principle and magic sizes of transition metal nanoclusters based on generalized wulff construction. Phys. Rev. Lett. 111, 115501 (2013).
Cao, D., Shen, T., Liang, P., Chen, X. S. & Shu, H. B. Role of chemical potential in flake shape and edge properties of monolayer MoS2 . J. Phys. Chem. C 119, 4294–4301 (2015).
Xie, Y., Wang, Z., Zhan, Y., Zhang, P., Wu, R., Jiang, T., Wu, S., Wang, H., Zhao, Y., Nan, T. & Ma, X. Controllable growth of monolayer MoS2 by chemical vapor deposition via close MoO2 precursor for electrical and optical applications. Nanotechnology 28, 084001 (2017).
Lauritsen, J. V., Kibsgaard, J., Helveg, S., Topsøe, H., Clausen, B. S., Laegsgaard, E. & Besenbacher, F. Size-dependent structure of MoS2 nanocrystals. Nat. Nanotechnol. 2, 53–58 (2007).
Rajan, A. G., Warner, J. H., Blankschtein, D. & Strano, M. S. Generalized mechanistic model for the chemical vapor deposition of 2D transition metal dichalcogenide monolayers. ACS Nano 10, 4330–4344 (2016).
Lee, C., Yan, H., Brus, L. E., Heinz, T. F., Hone, J. & Ryu, S. Anomalous lattice vibrations of single- and few-layer MoS2 . ACS Nano 4, 2695–2700 (2010).
Jeong, H. Y., Jin, Y., Yun, S. J., Zhao, J., Baik, J., Keum, D. H., Lee, H. S. & Lee, Y. H. Heterogeneous defect domains in single-crystalline hexagonal WS2 . Adv. Mater. 29, 1605043 (2017).
Liu, Z., Amani, M., Najmaei, S., Xu, Q., Zou, X., Zhou, W., Yu, T., Qiu, C., Birdwell, A. G., Crowne, F. J., Vajtai, R., Yakobson, B. I., Xia, Z., Dubey, M., Ajayan, P. M. & Lou, J. Strain and structure heterogeneity in MoS2 atomic layers grown by chemical vapour deposition. Nat. Commun. 5, 1–9 (2014).
He, K., Poole, C., Mak, K. F. & Shan, J. Experimental demonstration of continuous electronic structure tuning via strain in atomically thin MoS2 . Nano Lett. 13, 2931–2936 (2013).
Liang, L. & Meunier, V. First-principles Raman spectra of MoS2, WS2 and their heterostructures. Nanoscale 6, 5394–5401 (2014).
Amani, M., Burke, R. A., Ji, X., Zhao, P., Lien, D. H., Taheri, P., Ahn, G. H., Kirya, D., Ager, J. W. 3rd, Yablonovitch, E., Kong, J., Dubey, M. & Javey, A. High luminescence efficiency in MoS2 grown by chemical vapor deposition. ACS Nano 10, 6535–6541 (2016).
Amani, M., Lien, D. H., Kiriya, D., Xiao, J., Azcatl, A., Noh, J., Madhvapathy, S. R., Addou, R., Santosh, K. C., Dubey, M., Cho, K., Wallace, R. M., Lee, S. C., He, J. H., Ager, J. W., Zhang, X., Yablonovitch, E. & Javey, A. Near-unity photoluminescence quantum yield in MoS2 . Science 350, 1065–1068 (2015).
Liu, K., Zhang, L., Cao, T., Jin, C., Qiu, D., Zhou, Q., Zettl, A., Yang, P., Louie, S. G. & Wang, F. Evolution of interlayer coupling in twisted molybdenum disulfide bilayers. Nat. Commun. 5, 4966 (2014).
Suzuki, R., Sakano, M., Zhang, Y. J., Akashi, R., Morikawa, D., Harasawa, A., Yaji, K., Kuroda, K., Miyamoto, K., Okuda, T., Ishizaka, K., Arita, R. & Iwasa, Y. Valley-dependent spin polarization in bulk MoS2 with broken inversion symmetry. Nat. Nanotech. 9, 611–617 (2014).
Zhao, M., Ye, Z., Suzuki, R., Ye, Y., Zhu, H., Xiao, J., Wang, Y., Iwasa, Y. & Zhang, X. Atomically phase-matched second-harmonic generation in a 2D crystal. Light: Sci. Appl. 5, e16131 (2016).
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF-2015R1A3A2066337) and the DGIST Basic Research Program (17-BT-01) funded by the Ministry of Science and ICT of Korea.
Author contributions
J-HA planned and supervised the project. HK co-supervised the project. SMS performed the CVD growth of MoS2. KPD and SMS carried out the PL, Raman and absorption characterizations. XC performed the AFM imaging. KPD and HK performed the nonlinear optical characterization and analyzed the optical data. WSY and JDL performed the DFT calculations. KPD, SMS, XC, HK and J-HA wrote the manuscript.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information accompanies the paper on the NPG Asia Materials website
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Shinde, S., Dhakal, K., Chen, X. et al. Stacking-controllable interlayer coupling and symmetric configuration of multilayered MoS2. NPG Asia Mater 10, e468 (2018). https://doi.org/10.1038/am.2017.226
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/am.2017.226
This article is cited by
-
Combining ultrahigh index with exceptional nonlinearity in resonant transition metal dichalcogenide nanodisks
Nature Photonics (2024)
-
High-throughput computational stacking reveals emergent properties in natural van der Waals bilayers
Nature Communications (2024)
-
Controlling interlayer excitons in MoS2 layers grown by chemical vapor deposition
Nature Communications (2020)
-
Guide to optical spectroscopy of layered semiconductors
Nature Reviews Physics (2020)
-
Transition metal dichalcogenides bilayer single crystals by reverse-flow chemical vapor epitaxy
Nature Communications (2019)