Abstract
Surfaces designed to reduce the contact time of impacting droplets are potentially of great importance for fundamental science and technological applications, for example, anti-icing, self-cleaning and heating transfer applications. Previous studies have shown that the contact time can be reduced via introducing one or several crossing macroscale wires on superhydrophobic surfaces (SHSs). However, the impacts that strike far from the wires (off-center impacts) have contact times that are equal to those obtained on SHSs. Here we demonstrate that this problem can be largely solved by using macro anisotropic SHSs (macro-aniso-SHSs)—in which the wires are parallel and macroscaled. The droplet contact time depends on the spacing between the macrostripes and is remarkably reduced by 40–50% when the spacing is comparable to the droplet size. Obvious differences in the contact time are not observed for impacts that are centered on the stripe and in the groove. The impacts centered in the groove produce new hydrodynamics that are characterized by extended spreading, easy break up and bouncing in a flying-eagle configuration. The study discusses the underlying mechanisms of the impact processes. Moreover, the effect of parallel wires on the contact time is discussed by comparing the droplet impact data for grooved rice leaves and non-grooved cabbage leaves. The enhanced drop mobility associated with the macro-aniso-SHSs should be very useful in many industrial applications.
Similar content being viewed by others
Introduction
Inspired by biological systems in nature, the development of interfacial materials with enhanced drop mobility has a significant impact on a variety of fields, including self-cleaning,1, 2 drag reduction,3, 4 anti-icing5, 6 and anti-corrosion.7 In practical situations, surfaces are mostly placed under dynamic conditions with continuously impacting water droplets. For example, during the high-speed impact of supercooled (−50 °C) water droplets, aircraft surfaces are designed to compel water droplets to rebound off the surfaces before icing.8 Another example is the fast drop detachment from natural plants and biomimetic surfaces, which significantly decreases the likelihood of virus and bacteria deposition because many pathogens and diseases are transmitted through drops.9 Other examples include waterproof umbrellas and self-cleaning windshields. Therefore, the contact time of the entire impact process is considered to be crucial to these applications.8
Suitable surface designs could effectively reduce the liquid–solid contact time.10, 11, 12, 13, 14 Artificial superhydrophobic surfaces (SHSs) with contact angles larger than 150° are extremely low-energy surfaces that facilitate rapid drop bounce off due to the low friction between the drop and the substrate.15, 16, 17, 18, 19, 20, 21, 22, 23 The drops retain a circular symmetry during the first inertial-driven spreading stage and the second capillary-controlled recoiling phase. In addition, the contact time  is independent of the impact speed.12 Here, ρ, R and γ represent the density, radius and surface tension of the liquid drop, respectively. Bird et al.12 recently reported that the contact time can be reduced by adding a macroscopic wire (width and height >100 μm) on an SHS to induce asymmetric and fast recoil. With this method, when a drop impacted on a ridge that was much smaller than the drop size, it split into satellite droplets that led to an ~37% contact time reduction when compared with that on an SHS without wires. Gauthier et al.13 and Shen et al.8 further demonstrated that by fabricating macrotextured surfaces with different patterns, such as Y shapes and cross shapes, drops could be configured into different subunits and leave the surface with a reduced contact time. Liu et al. fabricated curved macrotextures (convex and/or concave) with curvatures that were comparable to the drop sizes.14 The drops spread larger in the azimuthal direction than in the axial direction and left the surface with an elongated shape perpendicular to the axial direction. As a result of the asymmetric momentum and mass distribution, there was a preferential fluid flow around the drop rim and the contact time was reduced by ~40%. These macrotextured surfaces can produce novel behavior with distinct impact dynamics and exert a pronounced influence on the contact time.
is independent of the impact speed.12 Here, ρ, R and γ represent the density, radius and surface tension of the liquid drop, respectively. Bird et al.12 recently reported that the contact time can be reduced by adding a macroscopic wire (width and height >100 μm) on an SHS to induce asymmetric and fast recoil. With this method, when a drop impacted on a ridge that was much smaller than the drop size, it split into satellite droplets that led to an ~37% contact time reduction when compared with that on an SHS without wires. Gauthier et al.13 and Shen et al.8 further demonstrated that by fabricating macrotextured surfaces with different patterns, such as Y shapes and cross shapes, drops could be configured into different subunits and leave the surface with a reduced contact time. Liu et al. fabricated curved macrotextures (convex and/or concave) with curvatures that were comparable to the drop sizes.14 The drops spread larger in the azimuthal direction than in the axial direction and left the surface with an elongated shape perpendicular to the axial direction. As a result of the asymmetric momentum and mass distribution, there was a preferential fluid flow around the drop rim and the contact time was reduced by ~40%. These macrotextured surfaces can produce novel behavior with distinct impact dynamics and exert a pronounced influence on the contact time.
Despite the significant progress made in previous studies, there is still a great problem: off-center impacts result in increased contact times (τ) that become similar to the values (τo) observed on an SHS.12, 13 Such inhomogeneities greatly limit applications, because the droplet mobility generally needs to be enhanced over an area rather than on a point or wire. To avoid such off-center impacts, the present work proposes that macro anisotropic SHSs (macro-aniso-SHSs) with more macroscopic parallel wires could be a promising solution since every droplet impact can be influenced by at least one or more wires. Moreover, altering the spacing between wires might allow the contact time to be tuned. Furthermore, the droplet impact in the groove could produce new impact dynamics, causing the impacting drop to spread in two opposite directions of the groove.
Droplet impacts on micro anisotropic SHSs (micro-aniso-SHSs) with major geometrical dimensions (the groove depth, width and solid pillar width) under 100 μm have been reported in several articles.24, 25, 26, 27 These impacts were characterized by elliptical spreading shapes but did not significantly reduce the contact time. The major-to-minor axis diameter ratios of the ellipses were observed to increase with the increasing cavity fraction and the surface slip had a negligible influence throughout the impingement process at low Weber numbers  where v is the impacting velocity. Although at high We values (on the order of 102), the surface slip had a significant influence. In this study, we fabricated macro-aniso-SHSs with different wire spacings using three-dimensional printing and nanoparticle deposition methods. We show how the marked reduction in the contact time varied with the stripe spacing and how the impacting drops interacted with multiple parallel wires to exhibit greatly different behavior at low We values. In addition, we report the first observation of new fascinating hydrodynamics in the form of a flying-eagle shape, which considerably differed from those on micro-aniso-SHSs.
where v is the impacting velocity. Although at high We values (on the order of 102), the surface slip had a significant influence. In this study, we fabricated macro-aniso-SHSs with different wire spacings using three-dimensional printing and nanoparticle deposition methods. We show how the marked reduction in the contact time varied with the stripe spacing and how the impacting drops interacted with multiple parallel wires to exhibit greatly different behavior at low We values. In addition, we report the first observation of new fascinating hydrodynamics in the form of a flying-eagle shape, which considerably differed from those on micro-aniso-SHSs.
Experimental procedures
Materials and methods
Surfaces with macro and micro stripes were fabricated with three-dimensional printing technology using an Envision TEC machine and E-Denstone 3SP (ENVISIONTEC GMBH, Gladbeck, Germany) as the material.
The fabrication of Macro-aniso-SHSs
The predesigned cross-sectional shape of the macrostripes was a triangle with 300 μm in base length and height. Samples were prepared with wire spacings equal to 400, 600, 800, 1000, 1200, 1400, 1800 and 2200 μm. All of the surfaces were treated with a polymer-particle solution that consisted of 1.0 g of hydrophobic-fumed silica nanoparticles and 3 ml of Capstone ST-200 in 17 ml of acetone.28 After evaporation and drying, the substrates and wires were coated with nanoparticles.
The fabrication of SHSs
Single SHS samples were prepared by spraying the same polymer-particle solution on a silica wafer as a control surface.
The fabrication of Micro-aniso-SHSs
Using high-resolution three-dimensional printing technology, microstriped surfaces with a center-to-center stripe spacing of 50 μm were easily created without a specific surface design. After depositing the nanoparticles, the micro-aniso-SHS was prepared as another control surface.
Drop impact procedure
Drops of deionized water, density ρ=0.998 kg m−3 and surface tension γ=72.8 × 10−3 N m−1, were dispensed from a calibrated needle. The radius (R) of the drops was 1.1 mm, as determined by measuring the weight of 10 drops on an analytical balance, which was reproducible with an uncertainty lower than 3%. The impact velocity (v) varied with the release height of the droplets. The impacts of the droplets on the surfaces were recorded at 4000 fps from different views, as shown in Scheme 1, using Olympus i-SPEED 3 cameras (ix Cameras Ltd., Rochford, UK). We defined the view parallel to the stripe as the x direction, the view perpendicular to the stripe as the y direction, the view 45 to the x axis in the xz plane as the α direction and the view 45 to the y axis in the yz plane as the β direction, respectively. Different scenes were obtained via different views as shown in Scheme 1. The overall contact time, which was determined using views along the x direction, was an average value of 10 impacts irrespective of the impact position. The contact time was defined as the time between the moment when the drop touched the surface, and that when the last fragment of liquid left the substrate. From each movie, v was determined from the successive positions of the center of the mass of the droplets before impact.
Results and discussion
Surface properties and the contact time
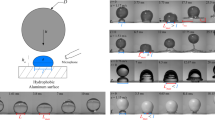
Figure 1 shows scanning electronic micrographs and contact angles on the macro-aniso-SHS (Figure 1). The top and side views of the macro-aniso-SHS (Figure 1a) indicate that the macrostripes were parallel and had predesigned triangle shapes at the cross-section with a base length and height of ~300 μm. The actual deviation from the predesigned size was <3%. Between the macrostripes, there were many microstripes, as magnified in Figure 1b. The center-to-center spacing of the microstripes was ~50 μm. The hydrophobic silica nanoparticle decoration is shown in Figure 1c, which rendered both the stripes and the grooves water-repellent. The prepared surface had three levels (macro/micro/nano) structures and the biggest difference between the layers and those in conventional anisotropic SHSs24, 25, 26, 27 was the presence of the macrotextured parallel stripes. Therefore, this surface is defined as a macro-aniso-SHS in the present article. To investigate the influence of the spacing size, we made eight macro-aniso-SHSs with macrostripe spacings ranging from 400 to 2200 μm. In addition, two control samples were also made: a conventional SHS with only a nanoparticle coating (Supplementary Figure S1) and a micro-aniso-SHS with microstripes (Figure 1b).
Surface characterization and water contact angles. (a) Scanning electronic micrograph (SEM) images of a single macrostripe-textured substrate with spacings=1000 μm. Top: the top view (along z axis). Bottom: the side view (along x axis). (b) SEM images of microstripes with an ~50 μm spacing. Top: the top view; bottom: the side view. (c) Close-up view of the texture shows the decoration consisting of aggregates of colloidal beads with a typical size of 20 nm. (d) The x and (e) y views of the water contact angles on the macro-aniso-SHS with macrospacings varying from 400 μm to 2200 μm. All of surfaces are water repellent, but their apparent contact angles show anisotropic properties.
The SHS sample exhibited a contact angle of 156°±1.4° (the inset in Supplementary Figure S1a). The micro-aniso-SHS exhibited anisotropic superhydrophobic behavior with contact angles of 159°±1.1° and 154°±0.4° in the x and y directions (Supplementary Figure S2a and b), respectively. The images of the water drops on the macro-aniso-SHSs (Figure 1d) along the x direction show a shift from a flat droplet bottom (spacing=400 μm) without macrocavity entry to a curved bottom with partial entry in the macrocavity (400 μm
We defined τ0 as the corresponding contact time on the SHS and τ as the contact time in the presence of the parallel wires; τo and τ were plotted as a function of the spacing in Figure 2a, in which the impact velocity (v) is between 86 and 121 cm s−1. The reference contact time (τo) in the black rectangle is in the range of 11–12 ms for different impacting velocities and it was scaled as the inertial capillary time 2.60–2.84 In the presence of the microstripes, the contact time slightly decreased to 10–11 ms. Regarding the macro-aniso-SHSs, the contact time was strikingly reduced (Figure 2a). The contact time decreased as the spacing increased and then a plateau was achieved with spacings >1000 μm, in which the contact time markedly reduced to ~6 ms. This value was 45–50% lower than that observed for the SHS and 40–45% lower than that observed for the micro-aniso-SHS in the gray rectangle.
In the presence of the microstripes, the contact time slightly decreased to 10–11 ms. Regarding the macro-aniso-SHSs, the contact time was strikingly reduced (Figure 2a). The contact time decreased as the spacing increased and then a plateau was achieved with spacings >1000 μm, in which the contact time markedly reduced to ~6 ms. This value was 45–50% lower than that observed for the SHS and 40–45% lower than that observed for the micro-aniso-SHS in the gray rectangle.
The relationship between the contact time and stripe spacing. (a) The contact time as a function of spacing at different impact velocities. The black and gray rectangles represent the contact times on the SHS and micro-aniso-SHS, respectively. When the spacing is larger than 1000 μm, the contact time decreases by 40–50% compared with the velocity on the SHS (spacing=0) and the micro-aniso-SHS (spacing=50 μm). (b) The contact time difference between impacts centered in the groove and on the stripe (τgroove−τstripe) is plotted as a function of the impact velocity.
The farthest position from the stripe was in the middle of the groove. The contact times of the impacts centered on the stripe and in the groove (Supplementary Figure S3) were compared and the differences between them (Figure 2b) were calculated, to determine the maximum influence of the impact position on the contact time. For the four macro-aniso-SHSs with stripe spacings=1200, 1400, 1800 and 2200 μm, both impacts showed a contact time of ~6 ms when the impact velocity was larger than 80 cm s−1 (Supplementary Figure S3). The contact time difference (τgroove−τstripe) between the two impact centers was <2 ms (Figure 2b). Such a small difference confirmed our hypothesis that the macro-aniso-SHSs could solve the off-center impacting problem to a great extent.
When the spacing size was continually increased, the contact time with the impact center on the stripe remained constant (Supplementary Figure S4), whereas the contact time with the impact center in the groove increased gradually and reached a similar contact time as that of the micro-aniso-SHS control sample (Supplementary Figure S5). Therefore, a suitable spacing range should be chosen in order to reduce the contact time.
Supplementary Figure S1b and c shows that the impact on the SHS exhibited typical circular spreading and retraction with a smooth rim at an impact velocity of v=121 cm s−1. The contact time on the SHS was 11.5 ms. At the same speed, the impact on the micro-aniso-SHS was similar to that on the SHS, but the rim exhibited undulations during the spreading stage (Supplementary Figure S2c), in agreement with previous reports.25, 26 The maximum spreading factors (the ratio of the maximum spreading diameter to the initial diameter of the drop) along the x and y directions were 2.59 and 2.47, respectively (Supplementary Figure S2f and g). Therefore, the spreading shape was oblong and the momentum was slightly greater along the x direction than the y direction. The contact time on the micro-aniso-SHS was 10.5 ms, 8.7% less than that on the SHS. The small reduction in the contact time on the micro-aniso-SHS was ascribed to the momentum anisotropy.14
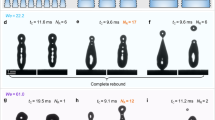
Figure 3a shows snapshots of the impact on the macro-aniso-SHS with a narrow spacing of 400 μm at an impact velocity of v=121 cm s−1. Viewed along the x direction, as shown in Figure 3a, the spreading film mainly remained above the stripes, although the middle part penetrated into the macrostructures. Then, the spreading drop recoiled and bounced without being broken by the stripe after 8.0 ms (Supplemantary Movie S1). The α and β views show that the impacting drop spread into a rough diamond shape (at 1.8 ms) and two tiny droplets were ejected along the x direction (at 3.3 ms) (Supplemantary Movie S1). Subsequently, the retraction was more prominent along the y direction than the x direction (α view), indicating that the momentum easily focused along the parallel line. Meanwhile, the β view shows that the drop continued to split along the parallel direction during the retraction stage (6.8 ms) and bounced off the surface after 8.3 ms (Supplemantary Movie S1). The fragmenting water droplets and anisotropic momentum resulted in overall contact times that were ~15–30% less than those on the control surfaces without any macrotexture.
The comparison of the droplet impacts on narrow and wide spacing surfaces when viewed from the x, α and β directions. (a) Selected snapshots of the impact on the macro-aniso-SHS with a narrow spacing of 400 μm. (b) Selected snapshots of the impact on the stripe of a macro-aniso-SHS with a wider spacing of 1200 μm. (c) Selected snapshots of the impact in the groove of a macro-aniso-SHS with a wider spacing of 1200 μm. For more details, see Supplemantary Movie S1.
Furthermore, the impacts on the macro-aniso-SHS with a wider spacing of 1200 μm (Figures 3b and c) show striking differences from those on the surfaces described above. Viewed along the x direction, the drop divided into two parts after striking on the stripe. The two rapidly spreading parts were abruptly slowed by the two side stripes, leading to hydraulic jumping at 5.5 ms. By contrast, the drops that impacted directly in the groove (Figure 3c) were split into three parts by the two stripes (x view). Viewed along the α and β directions, the drops that struck on the stripe adopted a butterfly spreading shape at 1.8 ms during the spreading stage and finally jumped off into two separate V shapes at 5.5 ms. During the lifting process, more satellite droplets were produced (β view). Notably, the impacting drop that centered in the groove spread into three grooves, resembling a pigeon or dragonfly. The part in the middle groove spread farther in two opposite directions along the x direction (α view), rebounded in the shape of a flying eagle at 6.5 ms (β view) and split into several child droplets in the air (α and β view). In these two cases, a large amount of liquid entered the macroscopic grooves. As the thickness of the spreading film was comparable to the height of the stripes, the stripes with wide spacings had a stronger tendency to redistribute and even fracture the spreading droplet during the impact. As a result, the impacts on the stripe with wide spacings exhibited much-reduced contact times by ~40–50% compared with those on the control surfaces.
Flying-eagle bouncing when the center of impact occurred in the groove
Based on the above observations, the impact position did not significantly affect the contact time, but it markedly influenced the hydrodynamic behavior. In particular, the new hydrodynamic phenomena needed to be elucidated, including the macrogroove confining the spreading, fragmentation and flying-eagle shaped bouncing phenomena. To the best of our knowledge, this behavior has not been previously reported.
To analyze the mechanism of the new hydrodynamics more conveniently, the impacts at a lower speed of v=86 cm s−1 were used as examples. Figure 4 shows a comparison of the droplet impacts on the micro-aniso-SHSs and macro-aniso-SHSs viewed along the y and β directions. The analysis of these impacts along the x axis is given in Supplementary Figure S6. The impacts on the micro-aniso-SHS generated round-like spreading and recoiling, and the drop finally rebounded with a tiny droplet ‘jet’ along the vertical direction (Figure 4a). However, the impact in the groove of the macro-aniso-SHS exhibited more curved spreading at 2.5 ms and a flying-eagle shape at 5.0 ms when the edges continued to spread while the contact line began to retract (Figure 4b). Two rough spherical droplets were emitted from the wings during the spreading stage. Then, new wings grew at 6.3 ms and became detached from the body after the eagle lifted off the surface at 8.0 ms. The first set of broken child droplets (droplets 1) continued flying toward both sides, while the second set of broken child droplets (droplets 2) withdrew to the middle part at 12.0 ms. This horizontal splitting behavior was in sharp contrast to the vertical ‘jet’ behavior observed on the micro-aniso-SHS.
Hydrodynamics comparison of the impacts on the micro-aniso-SHS and macro-aniso-SHS with impacts centered in the groove with an impact speed of 86 cm s−1. (a) Selected snapshots obtained with the y and β views on the micro-aniso-SHS. (b) Selected snapshots obtained with the y and β views the macro-aniso-SHS. The blue dashed lines track the trails of the first and second broken child droplets. The black double-headed arrow refers to the spreading length and the red arrow refers to the contact length. (c) Variation in the spreading factor and contact factor as a function of the elapsed time. (d) Variation in the spreading speed and contact speed as a function of the elapsed time. For more details, see Supplemantary Movie S2.
The flying eagle was characterized by expressing the variations in the spreading factor and the contact factor along the y direction as a function of the elapsed time (Figure 4c). The dimensionless factor L/D0 was defined as the ratio of the spreading or contact length (L) to the initial diameter of the drop (D0). The spreading length referred to the distance between the two outermost edges of the drop, even when not contacting the substrate, regardless of whether the drop was a single mass or had broken into fragments. The contact length was defined as the distance between the two outermost contact points of the drop and the substrate. The micro-aniso-SHS datasets (the upper figure in Figure 4c) show that the contact factor (red line) was slightly lower than the spreading factor (black line), but both plots exhibited the same moving trend (similar to those on the SHS in Supplementary Figure S1d and the micro-aniso-SHS in Supplementary Figure S2g and h). The maximum values of L/D0 were 1.97 for the spreading factor and 1.83 for the contact factor at 2.5 ms. Afterwards, the drops recoiled until the contact factor decreased to 0 at 10.5 ms. However, the results on the macro-aniso-SHS were strikingly different, showing not only an enhanced maximum spreading factor and contact factor but also a pronounced divergence between the two during the retraction stage (the lower figure in Figure 4c). The spreading factor and the contact factor for the impact in the groove increased to 2.72 and 2.49, respectively, at 2.5 ms during the spreading stage. Surprisingly, the spreading factor continued to grow when the contact factor quickly decreased to 0 at 6.5 ms (Figure 4c'), indicating that the edges were still expanding when the droplet left the interface and broke in the air. The large divergence between the spreading and contact factors indicated that the wings lifted first and the middle body part lifted off afterward, just as an eagle spread its wings to fly.
By multiplying the slope of the curves in Figure 4c with the radius of the droplet, the motion speeds of the different parts were determined, as shown in Figure 4d. The spreading speeds of the two edges at 1 ms were 54 cm s−1 and 103 cm s−1 for the micro-aniso-SHS and macro-aniso-SHS, respectively, indicating that the spreading speed was greatly accelerated by the macrogroove. Meanwhile, the moving speeds of the spreading edges and contact line of the impacting drop on the micro-aniso-SHS were highly correlated with each other. After 2.5 ms, both speeds turned from positive to negative, indicating that they were retracting. Their retracting speed was in the range of 20–40 cm s−1. For the macro-aniso-SHS, there was a larger divergence between the spreading speed and the contact speed after 2 ms. The spreading speed was always positive, indicating that the drop in the groove continually spread, even after 2.5 ms. In addition, there was a trough where the retraction speed of the contact line reached 133 cm s−1 at 5 ms, which was much higher than that on the micro-aniso-SHS. Therefore, the groove not only accelerated the spreading speed of the side edges but also increased the retraction speed of the contact line, which led to the large divergence in the spreading and contact factors.
Here, a simple mechanism is proposed to interpret the above-observed easy-breaking character observed as Figure 5 shows. Owing to the geometric confinement, the spreading drop in the groove had to concentrate its momentum in two opposing directions, leading to an extended spreading length and accelerated spreading speed. In addition, the entrained gas film below the leading edges resulted in more curved spreading and created a liquid neck, which collapsed with time due to capillarity.29 The increase in the spreading velocity led to an increase in the capillary number  where η is the viscosity of the liquid and U is the moving speed of the spreading drop and in turn triggered the instability of the edge sides and the resulting easy break-up behavior.
where η is the viscosity of the liquid and U is the moving speed of the spreading drop and in turn triggered the instability of the edge sides and the resulting easy break-up behavior.
Schematic mechanism of the hydrodynamics of the drop impact in the groove. (a) The hydrodynamics model of the flying-eagle and break-up behavior in the groove. (b) The spreading state shows different wetting statuses for the different parts. (A) The central part of the impacting droplet enters in the groove cavity and exhibits a Wenzel state. (B) The adjacent parts of the impacting droplet enter into the groove cavity and show a transition state between the Cassis and Wenzel state. (C) Both sides of the impacting drop enter into the groove cavity but do not touch the bottom of the groove, showing a suspended state.
The spreading state of the drop after impacting the substrate (Figure 5b) had a dominant role in its subsequent behavior. Driven by the increased inertial force due to momentum anisotropy, the drop spreading was also bound by an additional inward retraction force, that is, the Laplace force  (where θ is the apparent contact angle and r is the width of the groove or spacing between two stripes), which was generated by the groove. This force is related to the contact model of the droplet and the groove. Upon impinging the surface, the central part of the spreading droplet entered the groove cavity more easily than the edge sides (Figure 5b). Therefore, three states could occur during drop spreading in the groove. The central part of the impacting droplet enters into the groove cavity and exhibits a Wenzel state (state A), the adjacent parts of the impacting droplet bend into the groove cavity and show a transition state between the Cassis and Wenzel state (state B), and both edges of the spreading drop enter the groove cavity but do not touch the groove, exhibiting a suspended state (state C). As a result, the edge parts in state C, without touching the groove, spread the fastest due to the absence of an additional retraction force. The adjacent parts spread slower and the central part was the lowest because of the additional retraction force according to their contact area with the groove. In other words, the total frictional resistance in groove has been shown to be significantly reduced when the liquid phase does not enter the groove cavity regions.30, 31 The differences in speed were evidenced by the moving directions between the first and second child droplets shown in Figure 4b. In addition, due to the additional inward Laplace force, the retraction of the contact line was also accelerated by the groove when the edges were still expanding outward. Thus, the synergy of the accelerated spreading edges and the increased retraction of the contact line led to the flying-eagle shape and easy fragmentation characteristics of the new hydrodynamics.
(where θ is the apparent contact angle and r is the width of the groove or spacing between two stripes), which was generated by the groove. This force is related to the contact model of the droplet and the groove. Upon impinging the surface, the central part of the spreading droplet entered the groove cavity more easily than the edge sides (Figure 5b). Therefore, three states could occur during drop spreading in the groove. The central part of the impacting droplet enters into the groove cavity and exhibits a Wenzel state (state A), the adjacent parts of the impacting droplet bend into the groove cavity and show a transition state between the Cassis and Wenzel state (state B), and both edges of the spreading drop enter the groove cavity but do not touch the groove, exhibiting a suspended state (state C). As a result, the edge parts in state C, without touching the groove, spread the fastest due to the absence of an additional retraction force. The adjacent parts spread slower and the central part was the lowest because of the additional retraction force according to their contact area with the groove. In other words, the total frictional resistance in groove has been shown to be significantly reduced when the liquid phase does not enter the groove cavity regions.30, 31 The differences in speed were evidenced by the moving directions between the first and second child droplets shown in Figure 4b. In addition, due to the additional inward Laplace force, the retraction of the contact line was also accelerated by the groove when the edges were still expanding outward. Thus, the synergy of the accelerated spreading edges and the increased retraction of the contact line led to the flying-eagle shape and easy fragmentation characteristics of the new hydrodynamics.
Supplementary Figure S7 shows that the extended spreading, break-up and flying-eagle behavior in the groove became increasingly intense with the increasing impact velocity. At 3.0 ms, the spreading factor increased from 2.27 to 5.82 when the impact velocity increased from 71 to 121 cm s−1. As the impact speed increased, the wings elongated and tended to split into more child droplets (from 3 to 5, 7 and 9). Moreover, the fragmentation occurred earlier with the increasing impact velocity. The impact drop broke up at 7.5 ms with an impact speed of 71 cm s−1, 7.3 ms at 80 cm s−1, 5.0 ms at 101 cm s−1 and 2.5 ms at 121 cm s−1. These results show that the break up of the spreading droplet in the groove was prompted by the increased inertia. Finally, all of the droplets exhibited the flying-eagle shape at the right time, which was characterized by the formation of two elongated wings as the impact velocity increased.
Supplementary Figure S8 shows the critical Weber number (Wec) for drop break up in the groove as a function of the spacing. Herein,  where vc is the critical impact velocity for the drop to break up. The impacting drop split more easily on the macro-aniso-SHSs. The transition of the instability from the vertical to the horizontal direction decreased from medium We values (Wec>40) for the two control surfaces to low Wec values (Wec<20) for the macro-aniso-SHSs (Supplementary Figure S8a). Among the macro-aniso-SHSs, the smallest Wec (7.5) occurred when the spacing was equal to 1400 μm (Supplementary Figure S8b). Wec increased again for surfaces with a larger spacing, which may have been due to a slight decrease in the momentum anisotropy.
where vc is the critical impact velocity for the drop to break up. The impacting drop split more easily on the macro-aniso-SHSs. The transition of the instability from the vertical to the horizontal direction decreased from medium We values (Wec>40) for the two control surfaces to low Wec values (Wec<20) for the macro-aniso-SHSs (Supplementary Figure S8a). Among the macro-aniso-SHSs, the smallest Wec (7.5) occurred when the spacing was equal to 1400 μm (Supplementary Figure S8b). Wec increased again for surfaces with a larger spacing, which may have been due to a slight decrease in the momentum anisotropy.
W bouncing when the center of impact occurred on the stripe
Previously, Bird et al.12 analyzed the hydrodynamics of a droplet impact on a stripe that induced asymmetric and fast recoiling and thus exhibited a butterfly spreading shape. Therefore, to analyze the hydrodynamics of the drop impact centered on the stripe, it was most important to determine the influence of the two side stripes after drop impact. Figure 6 shows a comparison of impacts interacting with a single stripe and three stripes. As shown for the α view in Supplementary Figure S9, the spreading shapes of the drops after impacting on the single stripe and three stripes were similar. The x view of the impact on the single stripe (Figure 6a) without side stripes shows that the drop spread to the two sides and bounced off as an inverted bow. However, when the two side stripes were present, the drop spreading was greatly confined along the y direction (Figures 6b and d). The maximum spreading factor and the contact factor on the single stripe reached 2.85 (at 7 ms) and 1.90 (at 2.5 ms), respectively. However, they decreased to 1.92 (at 7 ms) and 1.50 (at 4 ms), respectively, when the two interplaying side stripes significantly retarding the spreading edges and contact line. Second, because of the two side stripes, the spreading droplet exhibited an obvious ‘hydraulic jump’, and finally bounced off the surface in the shape of a W. This behavior was quite different from the inverted bow shape observed for the droplet that impacted on the single stripe.
Hydrodynamics diagrams showing the different droplet impacts on the single-stripe surface and macro-aniso-SHS. (a) The hydrodynamics of a falling droplet interacting with a single stripe. (b) The hydrodynamics of a falling droplet interacting with three stripes. The black arrow: resistance; the red arrow: the inertial force (moving trend). (c) Variation in the spreading factor and contact factor as a function of the elapsed time on a single-stripe surface. (d) Variation in the spreading factor and contact factor as a function of the elapsed time on the macro-aniso-SHS.
Supplementary Figure S10 shows the hydrodynamics viewed along the y axis. According to the y view on the single-stripe surface (Supplementary Figure S10a), the spreading edge and contact line were not easily distinguished (Supplementary Figure S10c), probably because the view of droplet boundary was blocked by the stripe (Figure 6a). For the macro-aniso-SHS (Supplementary Figure S10b), the spreading increased due to the hydraulic jump and the contact line moved along the side stripes, so they were obviously identified (Supplementary Figure S10d). Moreover, there was an obvious divergence between the spreading edge and contact line, as shown in Supplementary Figure S10d. This divergence was caused by the hydraulic jump in the presence of the side stripes.
Based on the above analysis, the hydrodynamics of impact on the stripe along the x view are illustrated in the scheme in Figure 6 to compare the situation between the three-stripe and single stripe surfaces in order to understand the role of the two side stripes. Basically, the two side stripes had two roles: they provided an energetic barrier to block the spread of droplets and induced W bouncing due to the ‘hydraulic jump’.
Similarity in nature
In addition, we have searched to determine if a similar system exists in nature. The typical anisotropic SHS found in nature is the rice leave (Oryza sativa Linanaeus). It was recently determined that the macrostructure is the most important factor for interpreting the anisotropic sliding behavior among the three-level structures (macro/micro/nano) of rice.32 We also utilized the common superhydrophobic cabbage surface (Brassica oleracea L)33, 34 without grooves as a control surface. We performed the same impact experiments on these two surfaces, and their surface structure, impacting hydrodynamics and contact times are summarized in Figure 7. The cabbage leaf surface was characterized as having a micronanostructured morphology (Figures 7a1 and a2). Figures 7b1 and b2 show that the rice leaf surface consisted of macrostripes (width ≈140 μm, spacing ≈1000 μm), microstripes (Figure 7b3, width ≈88 μm and spacing ≈135 μm) and smaller mastoid arrays on each stripe and in each groove. Figure 7c shows that the droplet impacts on the cabbage leaf presented regular hydrodynamics with a contact time of approximately 12 ms at an impact velocity of 121 cm s−1. Figure 7d shows that the water impact on the rice leaf centered on the stripe also exhibited butterfly-shape spreading and the center stripe divided the liquid into two parts, similar to the behavior observed on the macro-aniso-SHS shown in Figure 3b. Figure 7e shows that the impact on the rice leaf centered in the groove was characterized as having a pigeon or dragonfly spreading shape and the spreading in the middle part was markedly extended and accompanied by droplet splitting, similar to the behavior observed on the macro-aniso-SHS shown in Figure 3c. Both types of impacts on the rice leaves had a contact time of ~6 ms and easy break-up properties (Supplementary Movie S3). Figure 7f shows that the contact time was reduced on the anisotropic superhydrophobic rice leaves by 25–50% compared with that on the superhydrophobic cabbage leaves. In addition, it was found the droplet broke up more easily at low hitting speeds (low We) in the horizontal direction on the rice leaves than on the cabbage leaves. The critical horizontal hitting speeds for droplet break up were 80±5 cm s−1 (We=9.7) and 190±8 cm s−1 (We=54.5) for the rice and cabbage leaves, respectively. Therefore, the results shown in this article indicate a general phenomenon that results from a macrotextured geometry that can provide guidance for bionic interface manufacturing or pesticide deposition.
The comparison between the surface structure, hydrodynamics and contact times for impacts on cabbage and rice leaves. (a1 and a2) The optical and scanning electronic micrograph (SEM) photographs of the cabbage leaf. (b1, b2 and b3) The optical and SEM photographs of the rice leave. (c) The selected snapshots of a water drop impacting on the cabbage leave. (d) The selected snapshots of a water drop impacting on the rice leaf with the impact centered on the stripe. (e) The selected snapshots of a water drop impacting on the rice leaf the with impact centered in the groove. The tested impact velocity in c–e is 121 cm s−1. (f) The contact time (τ) comparison for water droplets impacting on cabbage leaves and rice leaves. For more details, see Supplemantary Movie S3.
Conclusion
In this work, the impacts of droplets on macro-aniso-SHSs were studied and the results revealed that the contact time depended on the spacing between the macrostripes and was remarkably reduced by 40–50% when the spacing was comparable to the droplet size. The impact position did not obviously influence the contact time but markedly affected the hydrodynamics. A new type of hydrodynamics, characterized by elongated spreading, easy fragmentation and flying-eagle bouncing, was produced when the impact was centered in the groove. This finding challenges the previous understanding relating the instability transition from vertical to horizontal instability. Future research will focus on controlling the hydrodynamics and determining the mass/momentum transfer and energy transformation due to the macrotextured surfaces. The macro-aniso-SHSs with enhanced drop mobility may be excellent candidates for enhanced water repellency and other applications. In addition, the simple method (three-dimensional printing and spraying) for building macroscaled (or multilevel) anisotropic SHSs is scalable for manufacturing. Thus, we envision that the macro-aniso-SHS results will not only extend our fundamental understanding of classical impacting phenomena but also enable a wide range of applications.

Schematic illustration of the experimental setup used to record the impact of a water droplet on a macro-aniso-SHS substrate using a high-speed camera with different views (x, y, α, β).
References
Kamegawa, T., Shimizu, Y. & Yamashita, H. Superhydrophobic surfaces with photocatalytic self-cleaning properties by nanocomposite coating of TiO2 and polytetrafluoroethylene. Adv. Mater. 24, 3697–3700 (2012).
Deng, X., Mammen, L., Butt, H. J. & Vollmer, D. Candle soot as a template for a transparent robust superamphiphobic coating. Science 335, 67–70 (2012).
Mertaniemi, H., Jokinen, V., Sainiemi, L., Franssila, S., Marmur, A., Ikkala, O. & Ras, R. H. A. Superhydrophobic tracks for low-friction, guided transport of water droplets. Adv. Mater. 23, 2911–2914 (2011).
Solomon, B. R., Khalil, K. S. & Varanasi, K. K. Drag reduction using lubricant-impregnated surfaces in viscous laminar flow. Langmuir 30, 10970–10976 (2014).
Lo, C. W., Wang, C. C. & Lu, M. C. Spatial control of heterogeneous nucleation on the superhydrophobic nanowire array. Adv. Funct. Mater. 24, 1211–1217 (2014).
Hao, P. F., Lv, C. J. & Zhang, X. W. Freezing of sessile water droplets on surfaces with various roughness and wettability. Appl. Phys. Lett. 104, 161609 (2014).
Ma, J., Zhang, X. Y., Wang, D. P., Zhao, D. Q., Ding, D. W., Liu, K. & Wang, W. H. Superhydrophobic metallic glass surface with superior mechanical stability and corrosion resistance. Appl. Phys. Lett. 104, 173701 (2014).
Shen, Y., Tao, J., Tao, H., Chen, S., Pan, L. & Wang, T. Approaching the theoretical contact time of a bouncing droplet on the rational macrostructured superhydrophobic surfaces. Appl. Phys. Lett. 107, 11604 (2015).
Hao, C. L., Liu, Y. H., Chen, X. M., Li, J., Zhang, M., Zhao, Y. H. & Wang, Z. K. Bioinspired interfacial materials with enhanced drop mobility: from fundamentals to multifunctional applications. Small 12, 1825–1839 (2016).
Vollmer, D. & Butt, H. J. Fluid dynamics shaping drops. Nat. Phys. 10, 475–476 (2014).
Liu, Y. H., Moevius, L., Xu, X. P., Qian, T. Z., Yeomans, J. M. & Wang, Z. K. Pancake bouncing on superhydrophobic surfaces. Nat. Phys. 10, 515–519 (2014).
Bird, J. C., Dhiman, R., Kwon, H. M. & Varanasi, K. K. Reducing the contact time of a bouncing drop. Nature 503, 385–388 (2013).
Gauthier, A., Symon, S., Clanet, C. & Quere, D. Water impacting on superhydrophobic macrotextures. Nat. Commun. 6, 8001 (2015).
Liu, Y. H., Andrew, M., Li, J., Yeomans, J. M. & Wang, Z. K. Symmetry breaking in drop bouncing on curved surfaces. Nat. Commun. 6, 10034 (2015).
Kim, H., Park, U., Lee, C., Kim, H., Kim M, H. & Kim, J. Drop splashing on a rough surface: how surface morphology affects splashing threshold. Appl. Phys. Lett. 104, 161608 (2014).
Hao, P. F., Lv, C. J., Niu, F. L. & Yu, Y. Water droplet impact on superhydrophobic surfaces with microstructures and hierarchical roughness. Sci. Chin. Phys. Mech. 57, 1376–1381 (2014).
Marengo, M., Antonini, C., Roisman, I. V. & Tropea, C Drop collisions with simple and complex surfaces. Curr. Opin. Colloid 16, 292–302 (2011).
Liu, T. Y. & Kim, C. J. Turning a surface superrepellent even to completely wetting liquids. Science 346, 1096–1100 (2014).
Bartolo, D., Josserand, C. & Bonn, D. Retraction dynamics of aqueous drops upon impact on non-wetting surfaces. J. Fluid. Mech. 545, 329–338 (2005).
McCarthy, M., Gerasopoulos, K., Enright, R., Culver, J. N., Ghodssi, R. & Wang, E. N. Biotemplated hierarchical surfaces and the role of dual length scales on the repellency of impacting droplets. Appl. Phys. Lett. 100, 263701 (2012).
Chen, L., Xiao, Z., Chan, P. C. H., Lee, Y. K. & Li, Z. A comparative study of droplet impact dynamics on a dual-scaled superhydrophobic surface and lotus leaf. Appl. Surf. Sci. 257, 8857–8863 (2011).
Lu, Y., Sathasivam, S., Song, J. L., Crick, C. R., Carmalt, C. J. & Parkin, I. P. Robust self-cleaning surfaces that function when exposed to either air or oil. Science 347, 1132–1135 (2015).
Kwon, H. M., Paxson, A. T., Varanasi, K. K. & Patankar, N. A. Rapid deceleration-driven wetting transition during pendant drop deposition on superhydrophobic surfaces. Phys. Rev. Lett. 106, 036102 (2011).
Pearson, J. T., Maynes, D. & Webb, B. W. Droplet impact dynamics for two liquids impinging on anisotropic superhydrophobic surfaces. Exp. Fluids 53, 603–618 (2012).
Maynes, D., Johnson, M. & Webb, B. W. Free-surface liquid jet impingement on rib patterned superhydrophobic surfaces. Phys. Fluids 23, 052104 (2011).
Clavijo, C. E., Crockett, J. & Maynes, D. Effects of isotropic and anisotropic slip on droplet impingement on a superhydrophobic surface. Phys. Fluids 27, 122104 (2015).
Prince, J. F., Maynes, D. & Crockett, J. Jet impingement and the hydraulic jump on horizontal surfaces with anisotropic slip. Phys. Fluids 26, 042104 (2014).
Dong, Z., Ma, J. & Jiang, L. Manipulating and dispensing micro/nanoliter droplets by superhydrophobic needle nozzles. ACS Nano 7, 10371–10379 (2013).
Ledesma-Aguilar, R., Nistal, R., Hernandez-Machado, A. & Pagonabarraga, I. Controlled drop emission by wetting properties in driven liquid filaments. Nat. Mater. 10, 367–371 (2011).
Woolford, B., Maynes, D. & Webb, B. W. Liquid flow through microchannels with grooved walls under wetting and superhydrophobic conditions. Microfluid. Nanofluid. 7, 121–135 (2008).
Guo, T. Q., Che, P. D., Heng, L. P., Fan, L. Z. & Jiang, L. Anisotropic slippery surfaces: electric-driven smart control of a drop's slide. Adv. Mater. 28, 6999–7007 (2016).
Wu, D., Wang, J. N., Wu, S. Z., Chen, Q. D., Zhao, S. A., Zhang, H., Sun, H. B. & Jiang, L. Three-level biomimetic rice-leaf surfaces with controllable anisotropic sliding. Adv. Funct. Mater. 21, 2927–2932 (2011).
Neinhuis, C. & Barthlott, W. Characterization and distribution of water-repellent, self-cleaning plant surfaces. Ann. Bot. (Lond.) 79, 667–677 (1997).
Song, M., Ju, J., Luo, S., Han, Y., Dong, Z., Wang, Y., Gu, Z., Zhang, L., Hao, R. & Jiang, L. Controlling liquid splash on superhydrophobic surfaces by a vesicle surfactant. Sci. Adv. 3, e1602188 (2017).
Acknowledgements
We thank the National Research Fund for Fundamental Key Projects (2014CB932203) and a scientific and technological project of the Henan Province of China (122102210051).
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information accompanies the paper on the NPG Asia Materials website
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Song, M., Liu, Z., Ma, Y. et al. Reducing the contact time using macro anisotropic superhydrophobic surfaces — effect of parallel wire spacing on the drop impact. NPG Asia Mater 9, e415 (2017). https://doi.org/10.1038/am.2017.122
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/am.2017.122
This article is cited by
-
Numerical Study of the Superhydrophobic Nature of Triply Periodic Minimal Surfaces (TPMS): Energy Characteristics of Droplet Impact, Spreading and Rebounding Phenomena
Iranian Journal of Science and Technology, Transactions of Mechanical Engineering (2024)
-
Facile fabrication of superhydrophobic sub-millimetric cone-shape pillars based on a single UV exposure to control drop impact dynamics
Journal of Mechanical Science and Technology (2024)
-
Rigid—flexible hybrid surfaces for water-repelling and abrasion-resisting
Friction (2023)
-
Oscillation Characteristics of Single Droplet Impacting Vertically on Smooth Surfaces Using Volume of Fluid Method
Microgravity Science and Technology (2021)