Abstract
The facile conduction of alkali ions in a crystal host is of crucial importance in rechargeable alkali-ion batteries, the dominant form of energy storage today. In this review, we provide a comprehensive survey of computational approaches to study solid-state alkali diffusion. We demonstrate how these methods have provided useful insights into the design of materials that form the main components of a rechargeable alkali-ion battery, namely the electrodes, superionic conductor solid electrolytes and interfaces. We will also provide a perspective on future challenges and directions. The scope of this review includes the monovalent lithium- and sodium-ion chemistries that are currently of the most commercial interest.
Similar content being viewed by others
Introduction
The facile conduction of alkali ions in a crystal is of critical importance in energy storage. Today, the dominant form of energy storage in consumer electronics is the rechargeable lithium-ion (Li-ion) battery,1, 2, 3, 4, 5 a device that functions entirely on the basis of the reversible transport of Li+ ions. With one of the highest energy densities of known energy storage technologies, Li-ion batteries are finding increasingly large-scale applications in electrified transportation and grid storage. In recent years, there has also been a resurgence of interest in rechargeable sodium-ion (Na-ion) batteries,6, 7, 8, 9, 10, 11, 12 which function on the same basic principle but with Na+ instead of Li+ because of concerns regarding the abundance and cost of lithium.
Figure 1 shows a representation of a rechargeable alkali-ion battery. The typical electrode in an alkali-ion battery is an intercalation compound, which, as the name implies, stores alkali ions by inserting them into its crystal structure in a topotactic manner. During discharge, A+ ions are transported from the anode, through the electrolyte and into the cathode. The reverse happens during charge. Throughout this review, we will adopt the customary terminology of defining the ‘cathode’ as the positive electrode during discharge, even though the formal definition of the cathode changes depending on whether the charging or discharging process is being referred to. Current cathodes are typically transition metal oxides, and the insertion/removal of each A+ in the cathode is accompanied by the concomitant reduction/oxidation of a transition metal ion to accommodate the compensating insertion/removal of an electron. Graphitic carbon is the most common anode.
The performance of a rechargeable alkali-ion battery depends crucially on the ease with which alkali ions move in the host crystal of the cathode and anode, in the electrolyte, and in the electrode–electrolyte interface. Poor alkali transport in any part of the battery leads to reductions in rate capability, practical capacity and cyclability. Typical Li-ion battery cathodes today exhibit Li+ diffusivities in the range of 10−7 to 10−12 cm2 s−1 at room temperature.13, 14, 15, 16, 17 The Li+ conductivity requirements in the electrolyte are significantly higher because of the larger diffusion length scales. The typical organic electrolyte used in today’s batteries, a solvent mixture of a cyclic carbonate such as ethylene carbonate and a linear carbonate such as dimethylcarbonate with LiPF6 salt, has a Li+ conductivity on the order of 10 mS cm−1 at room temperature.18, 19 Such flammable organic electrolytes are inherently unsafe and have limited electrochemical windows of ∼4.5 V. A promising alternative is to replace flammable organic electrolytes with solid ceramic superionic conductors to create ‘all-solid-state’ batteries. However, until recently, known solid electrolytes, such as the garnet Li7La3Zr2O12 and the perovskite Li3xLa2/3−xTiO3 (0⩽x⩽0.16), have Li+ conductivities that are at least 1–2 orders of magnitude lower compared with those of organic liquid electrolytes.20, 21 The discovery of the Li10GeP2S12 superionic conductor by Kamaya et al.22 in 2011, with the highest ever reported Li+ conductivity of 12 mS cm−1, has provided renewed hope for the development of solid ceramic electrolytes with comparable transport properties with flammable organic electrolytes.
Despite its great importance, the factors that determine alkali conductivity in materials remain poorly understood. Many proposed design ‘rules of thumb’ for fast alkali conductivity, for example, 3D interstitial networks with bottlenecks of sufficient size,23 the presence of alkali ion disorder,24 having a polarizable anion framework,25 body-centered cubic system close-packed anion frameworks,26 and so on, are limited to specific chemistries or structure types and are not readily generalizable. There has also been limited success in identifying new frameworks that share these features. Indeed, even the reasons for the different conductivities exhibited by different alkali ions (e.g., Li+ and Na+) are not well understood. Certainly, the significantly larger size of Na+ (102 pm) compared with Li+ (76 pm) could be expected to mean lower migration barriers for Li+ in bottle-neck-constrained crystals, such as the anion-close-packed olivine, but there is both experimental27 and theoretical11 evidence of more facile Na+ transport in the more open-layered and NAtrium SuperIonic CONductor (NASICON)-type structures. Furthermore, despite their chemical similarity, Na-ion chemistry can exhibit different crystal structures from Li-ion chemistry. A prime example of this is that layered NaMO2 (M=transition metal) exists in both P2 and O3 (following the notation of Delmas et al.28) forms, whereas LiMO2 exists only in the O3 form, and there are significant differences in alkali diffusion topology between P2 and O3.29
In this review, we survey the available computational methods for studying solid-state alkali diffusion, and how these methods have provided useful insights into rechargeable battery material design. The chemistries reviewed include both lithium and sodium ion chemistries. We have elected to not discuss multivalent chemistries and to keep this review focused on a single, critical battery property, solid-state alkali diffusion, targeting depth of discussion over breadth. Readers who are interested in the more general application of computational methods in the prediction of other battery properties and overall battery design are referred to other excellent reviews on this subject.30, 31, 32, 33
This review is structured in the following manner:
-
We first provide a comprehensive survey of the computational methods that are available for the study of solid-state alkali diffusivity and conductivity and outline the advantages and limitations of each method;
-
Next, we discuss how computational methods have been used in the study and design of various components of the alkali rechargeable battery;
-
Finally, we provide a perspective on the challenges and potential future developments in the application of computational methods to study alkali conductivity.
Computational approaches
The phenomenological theory of diffusion is extensively covered in many excellent textbooks.34, 35 Here, we will only present the key relationships used in computational simulations and models.
From irreversible thermodynamics, it can be shown that the self-diffusion constant D* is related to the velocity self-correlations of individual particles according to

More commonly, the alkali diffusivity is calculated from the corresponding Einstein relation:

where t is the time and d is the dimensionality of the lattice in which diffusion takes place. In essence, the diffusivity is given by the mean-square displacement averaged over all diffusing ions and over time t as an ensemble average.
When cross-velocity correlations between alkali ions are negligible (the Darken approximation), the diffusion constant D is then related to the self-diffusion coefficient D* as

where Θ is a thermodynamic factor.
To obtain the alkali conductivity from the diffusivity, one can make use of the Nernst–Einstein relation as follows:

where ρ is the molar density of A+ ions, z is the charge of A+ (z=+1), F is the Faraday constant, R is the gas constant, k is the Boltzmann constant, T is the temperature and ΔEa is the overall diffusion barrier energy.
Transition state theory and the nudged elastic band method
In many materials, alkali diffusion can be modeled using a lattice model, where the alkali atoms spend most of their time at well-defined equilibrium sites and only a small fraction of time along paths connecting adjacent sites. Diffusion arises from the migration or ‘hopping’ of an alkali ion from one site to a neighboring vacant site via an activated state that is located at the maximum energy point along the minimum energy path between the end points of the hop. The activation barrier ΔHa is then given by

where Ha is the enthalpy of the crystal in the activated state and Hi is the enthalpy of the crystal in the initial state. The frequency Γ at which a hop occurs is then given by transition state theory36 as

where ν is an attempt frequency, ΔS is the activation entropy, k is the Boltzmann constant and T is the temperature. Within the harmonic approximation, this equation can be simplified as follows:

where ν′ is related to the ratio of the product of the normal-mode frequencies of the initial state to the product of the normal-mode frequencies of the activated state.
In studies of alkali diffusion, the nudged elastic band (NEB) method37 is frequently used to determine the barriers for alkali migration paths for a specific nuclei configuration. In this method, a number of intermediate images along the migration path is optimized to find the lowest possible energy while maintaining spacing between neighboring images. This constrained optimization is achieved by adding ‘spring’ forces along the band between images and projecting out the component of the force due to the potential perpendicular to the band. Such a calculation would typically involve the following steps:
-
1)
Initial geometry optimization calculations of the host material with the alkali ion in the initial and final positions.
-
2)
An interpolation between the starting and ending structures to generate a series of ‘images’ along the migration path.
-
3)
An NEB calculation to find the lowest energy path along the saddle points.
In principle, the NEB method can be applied to determine the barrier of any migration event, be it a single ion/vacancy or a coordinated multi-ion motion. In practice, however, the identification of the relevant migration events and local environment for coordinated multi-ion motion (common in many solid electrolytes exhibiting alkali disorder) is highly challenging. For that reason, NEB calculations are usually carried out at the dilute limits, that is, either the migration of a single vacancy in an otherwise fully alkaliated structure or a single alkali migration in an otherwise alkali-free host structure. Furthermore, to obtain an actual diffusivity number, the prefactor in Equation (7) must be calculated or estimated. A typical value of 1013 is used, although it can also be obtained via first-principles calculations.
Kinetic Monte Carlo
The kinetic Monte Carlo (KMC) method is a Monte Carlo simulation method for the time evolution of natural processes. For studies of alkali diffusivity, it requires as input the environment-dependent activation barriers, which are usually obtained from NEB calculations. A first-principles cluster expansion is then performed to parameterize these barriers for Monte Carlo simulations. A basic outline of the KMC algorithm is given by Van der Ven38 as follows:
-
1)
We begin with an alkali-vacancy equilibrium arrangement, usually obtained via standard equilibrium MC simulations.
-
2)
All migration probabilities Γm are then determined based on the paths available to all alkali ions. Γm is zero if the end points of the migration path m are both occupied by alkali ions. Otherwise, Γm is calculated based on Equation (7).
-
3)
A random number ρ∈(0, 1] is then sampled, and the migration event k is chosen such that

where Γtot is the sum of all individual probabilities Γm. This ensures that each event m occurs with probability Γm/Γtot.
-
4)
The time is then updated by Δt, given by

where η∈(0, 1], and steps 2–4 are then repeated.
Molecular dynamics simulations
Molecular dynamics (MD) simulations model the motion of the mobile atoms/ions, including their vibration and migration, following Newtonian dynamics. The diffusion properties can be obtained by analyzing the real-time trajectory of atoms. Currently, most studies model the self-diffusion of atoms/ions at equilibrium conditions rather than under the driving force of some concentration gradient to obtain diffusion properties.
The typical steps of an MD simulation are as follows:
-
1)
The initial structure is usually statically equilibrated and initialized at a given temperature (typically chosen at 300 K or lower).
-
2)
The sample is then heated to the desired temperature using NVT (constant number (N), volume (V) and temperature (T)) ensemble.
-
3)
After the system is equilibrated at the desired temperature, MD simulation is performed using NVT or NPT (constant number (N), pressure (P) and temperature (T)) ensemble to model the self-diffusion of the atoms over time.
-
4)
After the MD simulation, an analysis of the trajectory of atoms, velocity time-correlation, and displacement-time dependence is performed to obtain diffusion properties.
MD simulations can provide a variety of diffusion properties of a material. The diffusion pathway and mobile carriers (e.g., vacancies or interstitials) can be directly observed from the trajectory of atoms during simulations. The diffusivity or conductivity of the atoms can be obtained using the Green–Kubo time-correlation of the velocity of the atoms (Equation (1)) or the corresponding Einstein relationship (Equation (2)). To obtain statistically significant and converged diffusivity, MD simulations need to be conducted over sufficiently long time scales such that a sufficient number of ‘hops’ or amount of diffusion takes place.
The main input to MD simulations is an accurate description of the interatomic interactions. Classical MD simulations use empirical potentials or force fields, such as those based on the Born model framework33, 39 and bond-valence methods.40 The empirical potentials are based on mathematical formulas and parameters that are fitted from experimental and ab initio calculation input. The key advantage of classical MD simulations is their significantly lower computation costs compared with ab initio methods. The low computation cost of empirical potentials allows the MD simulations to be performed on larger systems or for longer periods of time. However, the accuracy and transferability of empirical potentials are often questionable, and suitable potentials may not always be available, especially for new material systems. These limitations of empirical potentials hinder the wide application of classical MD simulations.
Recently, ab initio MD (AIMD) simulations have been adopted to study the alkali diffusion in solid electrolyte and electrode materials.41, 42 The use of ab initio methods to evaluate interatomic interactions overcomes the issues of empirical potentials by leveraging the predictivity of ab initio techniques to study new materials.41, 42 AIMD can be performed in either Born–Oppenheimer or Car–Parrinello manner.43
MD simulations provide unique insights into diffusion properties and diffusion mechanisms compared with other techniques, such as NEB and KMC. In MD simulations, prior knowledge of the diffusion mechanisms, such as the diffusion pathway, is not required. This makes MD a suitable technique for identifying and understanding diffusion mechanisms of new materials. Key diffusion properties, such as the diffusion pathway, activation energy, diffusivity and conductivity can be obtained from a set of MD simulations. In addition, MD simulations are able to capture the correlated motion of ions in a highly disordered mobile sublattice (such as Li in Li10GeP2S1244), which may be difficult to accomplish using NEB methods.
The major limitation of MD simulations, regardless of whether they are classical or ab initio, is the short accessible time scale, which is usually on the order of tens of picoseconds to microseconds. The total duration of an MD simulation is limited by the small time step, which is on the order of femtoseconds (10−15 s). The time step is chosen such that it is significantly smaller than the fastest process in the system, which is usually the vibration of atoms (∼1013 Hz). Hence, MD simulations are usually only performed for materials with fast diffusion, and many MD simulations, particularly those based on first-principles methods, are performed at elevated temperatures to accelerate diffusion processes. The diffusion properties obtained at elevated temperatures are then extrapolated to the temperature range of interest. This extrapolation is based on the assumptions that the diffusion mechanism is the same at the extrapolated temperature on the basis of the Arrhenius relationship and that no phase transition of the mobile ion sublattice occurs between the temperatures of MD simulations and the extrapolated temperatures.
Computational studies of alkali conductivity
In this section, we provide an overview of how the computational methods discussed in the previous section have been used in the study of alkali conductivity in rechargeable alkali-ion batteries. We have organized this section in terms of the key components of the rechargeable alkali-ion battery, namely, the cathode, anode and electrolyte. Historically, the cathode has been the target of intensive research in the pursuit for higher energy densities. It is therefore unsurprising that this component of the battery has the most varied chemistry and the largest body of work with regard to computational studies of alkali conductivity. Nevertheless, the anode and electrolyte have enjoyed renewed interested in recent years as well, particularly in the form of graphite alternatives, such as Si anodes and solid-state superionic conductor electrolytes.
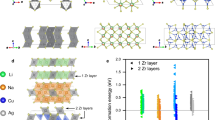
To give the reader a sense of the wide range of crystal structures exhibiting fast alkali conduction, we have summarized some of the representative crystal structures discussed in this section in Figure 2. In general, the diffusion topology of alkali-ion conductors can be distinguished in terms of the dimensionality, for example, 1D in olivine LiMPO4 and tavorites (Figures 2c and d), 2D in layered AMO2 and graphite (Figures 2a and j, respectively) and 3D in spinel, NASICON, garnet, regular and antiperovskites (Figures 2b, e, f, g and i, respectively). Notably, there is inherently a certain amount of subjectivity in such classifications; for example, Li10GeP2S12 (Figure 2h) can be classified as either a 3D conductor or a pseudo-1D conductor. As we shall see, the dimensionality of diffusion has important consequences for macroscopic conductivity in a material, as do the alkali migration barriers. A general rule of thumb is that, for electrode applications, percolating paths with alkali diffusion activation barriers of<600 meV (~58 kJ mol−1) are desired, whereas for solid electrolyte applications, activation barriers ideally need to be <300 meV (~29 kJ mol−1).
Cathodes
Layered AMO2
The layered materials with formula AMO2 (where A is an alkali ion and M is a transition metal or a mixture of transition metals) are the current dominant form of cathodes for rechargeable alkali-ion batteries. For example, LiCoO2 is the cathode of choice in commercial Li-ion batteries. Layered AMO2 materials are also of great interest in the Na-ion battery chemistry currently under heavy investigation. Although LiMO2 is synthesized only in O3, layered NaMO2 compounds can be synthesized in both the O3 and P2 stacking. In the O3 stacking, the alkali ion is in an octahedral site, whereasile in the P2 stacking, the alkali ion is in a prismatic site. In general, alkali diffusion in the O3 stacking is significantly more well studied than that in the P2 stacking, primarily because of the success of lithium-ion battery technology.
One of the earliest computational studies of diffusion in the O3 LiCoO2 is the work of Van der Ven et al.14 Using first-principles NEB simulations, the authors established that Li diffusion in the O3 structure occurs through a di-vacancy mechanism where a Li migrates between neighboring octahedral sites through a tetrahedral site. Using KMC simulations, the authors further showed that the Li+ diffusivity in LixCoO2 is low at x≈1, increases with decreasing lithium concentration until a maximum is reached at x≈0.65, but sharply decreases thereafter (see Figure 3), in good qualitative agreement with experiments.
Calculated chemical diffusion coefficient DC (□) and jump diffusion coefficient DJ (♦) of LixCoO2 as a function of x at 300 K from kinetic Monte Carlo (KMC) simulations. The diffusion coefficient reaches a maximum at x~0.75 and decreases with decreasing x. Reproduced with permission from Van Der Ven and Ceder14.
Later work by Kang et al.45 applied first-principles computational modeling to develop strategies to enhance the rate capability of layered materials (Figure 4). Using NEB calculations, they found that the combined use of low-valent transition-metal cations and low strain in the activated state leads to increased interlayer spacing, which significantly reduces the activation barriers for Li diffusion. A Li(Ni0.5Mn0.5)O2 with very little intralayer disordering to optimize those factors was synthesized via Li-for-Na ion exchange of Na(Ni0.5Mn0.5)O2, and the resulting material retains its capacity at much higher rates (6C) compared with similar cathodes synthesized via traditional solid-state routes. This effort demonstrated the power of complementing traditional laboratory experiments with computational modeling in material design.
Calculated activation barrier for Li migration in O3 Li(Ni0.5Mn0.5)O2 as a function of the Li slab space. Triangles and circles represent the activated state (tetrahedral site) that shared faces with Ni and Mn, respectively. The slab spacing has been determined for a hypothetically perfect layered system, for a system with 8.3% excess Ni present in the Li layer without a change in the transition-metal layer, and for a system with 8.3% Li-Ni exchange. The result shows that Li-Ni disorder leads to smaller slab spacing and higher activation barriers, especially at 16% delithiation. Reproduced with permission from Kang et al.45
In contrast, Na diffusion mechanisms in the P2 NaMO2 structure have only recently been elucidated by Mo et al.29 through the use of AIMD and NEB simulations. They demonstrated that Na+ diffusion in the P2 structure forms a hexagonal network topology, with alternating transition-metal face-sharing and non-face-sharing prismatic sites. Mo et al. showed that the P2 structure, unlike the O3 structure, supports fast Na conduction over a wide range of Na concentrations, which may account for the generally higher achieved capacities in P2 NaMO2.12, 46
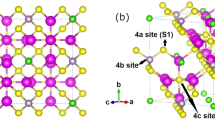
Spinel AM2O4
The spinel oxides are another promising class of lithium-ion battery cathodes. Lithium diffusivity in the commercial LiMn2O4 spinel has been studied using both empirical potentials47 and first-principles methods.48, 49, 50, 51 In general, these computational studies show that lithium diffusion in the spinel LiMn2O4 form a 3D network where lithium migrates between the tetrahedral 8a sites via the octahedral 16c sites. More recent studies also suggest that doping of the spinel with other transition metals, particularly with Cu or Co, can further reduce the barrier for Li migration.50, 51 In the case of Co, recent work by Nakayama et al. suggests charge disproportionation as the reason for the lowering of the migration barrier.51
At high temperatures, spinel compounds can transform into denser postspinel phases, such as CaMn2O4 (CM), CaFe2O4 (CF) and CaTi2O4 (CT). Using NEB calculations, Ling et al.52 found that the barrier for Li+ migration in CM phase is 120 meV, a much lower value compared with that in other cathode materials. Even for the larger Na+ ions, the migration barrier in the CM phase is <400 meV, comparable to that of Li+ migration in spinel LiMn2O4.
Rocksalt-type oxides
Both the layered O3 (not P2) LiMO2 and spinel LiM2O4 can be considered ordered members of a more general category of rocksalt (NaCl)-type oxides, where the oxygen anions form an fcc-like lattice and the cations are distributed in the fcc lattice of octahedral interstitials.53
A particularly exciting recent result is a unifying theory of the lithium exchange capacity in both disordered and ordered rocksalt-like structures based on percolation theory. For a material to demonstrate macroscopically facile alkali diffusion, it must contain low activation barrier paths for alkali migration, and these low activation paths must form a percolating network through the entire crystal. Urban et al.54 demonstrated that there is strong dependence of the lithium percolation thresholds on the cation ordering and lithium content in the layered α-NaFeO2 structure, the spinel-like LT-LiCoO2 structure and the γ-LiFeO2 structure (see Figure 5). The γ-LiFeO2-type structures generally lack good percolating Li migration channels, which would explain their relatively poor electrochemical performance. Alternately, the spinel-like structures have percolating low-activation energy networks that are insensitive to off-stoichiometry and cation disorder. For the layered structure, the authors demonstrated that a critical Li-excess concentration exists at which Li percolation occurs. These insights have led to the development of a cation-disordered Li1.211Mo0.467Cr0.3O2 oxide with a cycling capacity exceeding 250 mAh g−1.55
Critical lithium concentrations for 0-TM (transition metal) channel percolation as a functional of Li stoichiometry and cation mixing. For the layered structure, the percolation threshold reaches a minimum at 50% cation mixing. Reproduced with permission from Urban et al.54
Polyanion oxides
Since the discovery of LiFePO4 olivine in 1997, polyanionic oxides have attracted much attention as potential cathodes due to their higher voltages via the inductive effect.2, 56 The LiMPO4 (M=Fe, Mn, Co, Ni) family of olivines, in particular, has been extensively studied. Using NEB calculations, Morgan et al.17 first showed that olivine LiMPO4s are likely to be 1D conductors, with low migration barriers (<360 meV) along [010] chains but very high migration barriers (>1 eV) for interchain hopping. Qualitatively similar results were obtained by Islam et al.57 using empirical Buckingham potentials. In addition, Islam et al.57 also predicted that Li+ migration would follow a nonlinear, curved path in the olivine (Figure 6) and that the most favorable intrinsic defect is the Li-Fe ‘antisite’ pair, which is highly detrimental to Li+ migration. Malik et al.58 further demonstrated that, unlike 2D (e.g., layered AMO2) and 3D (e.g., spinel) diffusers, 1D diffusers, such as the olivines, are highly sensitive to channel-blocking defects, which makes nanosizing critical to achieving good electrochemical performance.
Curved Li diffusion pathway in LiFePO4 from empirical models. Similar results are obtained with ab initio density functional theory (DFT) methods and have been verified experimentally. Reproduced with permission from Islam et al.57
The olivine structure has also been investigated as a potential cathode for Na-ion battery chemistry.59, 60, 61 Unlike LiMPO4, NaMPO4 tends to prefer the maricite structure, which is similar to the olivine structure but with the alkali and transition metal swapping atomic positions.62 However, the maricite structure is uninteresting for battery applications given the lack of viable alkali diffusion pathways in the structure. Ong et al.11 previously performed a comparison of the alkali migration barriers in the olivine and layered structures using NEB calculations (Figure 7). They found that the Na migration barrier is slightly higher than the Li migration barrier in the olivine structure. However, another work by Tripathi et al.63 using empirical potentials found the opposite trend, that is, with Na diffusion barriers being lower compared with the Li migration barriers in olivine. In general, the barriers for Na migration in the olivine structure are relatively low, indicating that Na diffusion is likely to be facile in this structure.
Comparison of calculated barriers for Na+ and Li+ diffusion in the (a) layered O3 (di-vacancy mechanism) and (b) olivine structures. LCO: LiCoO2; NCO: NaCoO2, FP: FePO4; LFP: LiFePO4; NFP: NaFePO4. Na barriers are higher compared with Li barriers in close-packed olivine but lower compared with Li barriers in the more open-layered structure. Reproduced with permission from Ong et al.11
Pyrophosphates with the formula A2MP2O7 (M=Fe, Mn, Ni) have recently been investigated as potential cathode materials for both Li-ion and Na-ion chemistries.64, 65, 66, 67, 68 In general, both atomistic simulations and first-principles studies find these materials to be fast 3D conductors with low activation barriers for Li and Na migration.67, 68
Another class of phosphate cathodes that has enjoyed considerable interest is the tavorite family, with a structure similar to that of LiFe(PO4)(OH).69, 70, 71, 72, 73 Mueller et al.74 performed a comprehensive evaluation of tavorites as potential intercalation cathodes for Li-ion battery chemistry. In terms of diffusivity, they found that VOPO4, VOPO4F and FeOPO4 have reasonably low activation energies (200–500 meV) for Li migration in 1D but much higher activation energies in 2D and 3D (>700 meV). Ling et al.75 subsequently conducted a more detailed analysis of the various polymorphs of VOPO4,69, 76, 77, 78, 79, 80, 81, 82, 83 which are of particular interest because of their high theoretical capacities through multielectron cycling. They found relatively low migration barriers for 2D vacancy diffusion in α-LiVOPO4 and extremely low migration barriers (150 meV) in β-LiVOPO4. Tripathi et al.63, Adams et al.84 and Ramzan et al.85 have also studied the sulfate tavorite AFeSO4F using MD simulations with empirical, bond valence and ab initio-based potentials, respectively. These calculations generally agree that the most favorable alkali migration path is a zigzag [111] pathway, although the material itself exhibits 3D diffusion.
Other than the phosphates, silicates (Li2MSiO4)86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96 have also been studied as possible polyanion cathodes. Computational studies generally find fairly high Li migration barriers (0.9–2 eV) in the silicates, particularly in the delithiated structures.87, 88, 96
Solid-state superionic conductor electrolytes
NASICON-type structures
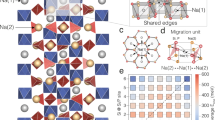
The term NAtrium SuperIonic CONductor (NASICON) refers to a family of materials with the general formula AMP3O12 (where A is an alkali ion and M is a transition metal) and a framework comprising MO6 octahedra and P(Si)O4 tetrahedra sharing common corners.23 Among the huge family, the solid solution Na1+xZr2P3−xSixO12 (NZPS) and Al-doped LiTi2(PO4)3 (LTP) are well-known alkali superionic conductors. Kumar et al.97 proposed a full interionic potential, with which they successfully reproduced the variation in the lattice constants and ionic conductivity as a function of composition in NZPS. Using this interionic potential, they found that the sum of site occupancy at Na(1) and mid-Na sites always adds up to unity and that the Na migration mainly occurs between Na(1) and Na(2) sites,98 which also agree well with observations from experiments. In a recent work, Lang et al.99 demonstrated an inverse relationship between the migration barrier and Li6O octahedra size in doped LTP from NEB calculations (Figure 8).
Plot showing a linear relationship between activation energies and LiO6 polyhedra volumes in LiX0.2Ti1.8(PO4)3. Reproduced with permission from Lang et al.99
LLTO perovskites
The lithium lanthanum titanium oxides (Li3xLa2/3−xTiO3, LLTO) are a family of lithium superionic conductors adopting a perovskite structure with A-site deficiency. The highest room temperature bulk ionic conductivity for LLTO reported is 1 mS cm−1.100 Catti modeled the A-site ordering of LLTO at three compositions, namely Li-rich (Li1/2La1/2TiO3), Li-intermediate (Li5/16La9/16TiO3) and Li-poor (Li1/8La5/8TiO3). His work showed that there is a significant layered distribution pattern and that the most stable structure has the maximum difference in terms of composition between two adjacent layers.101, 102 Based on these models, Catti further explored the migration barrier in LLTO with a ‘frozen ion’ approach.103, 104
Despite the high bulk ionic conductivity, the overall ionic conductivity of LLTO is usually poor, typically two orders of magnitude lower compared with their bulk ionic conductivity because of the high resistance at grain boundaries. Interesting work conducted by Moriwake et al.105 shows that the Li migration barrier over a 90° domain boundary fully occupied with La can be as high as 3.58 eV from NEB calculations. The barrier is reduced to 0.58 eV if the Li migrates via a La vacancy at the domain boundary, and it can be further reduced to 0.26 eV if the Li penetrates the domain boundary via the La-poor (Li-rich) layer, which is nearly the same as the barrier found in bulk LLTO.
LLZO garnet
Fast Li+ conduction in cubic garnet-type Li7La3Zr2O12 (LLZO) compounds was first reported by Murugan et al.106 Subsequently, Awaka et al.107 also synthesized the tetragonal phase of LLZO at lower temperature, but its ionic conductivity is two orders of magnitude lower than the cubic phase. Jalem et al.24 identified a concerted Li+ migration mechanism in cubic LLZO via AIMD simulations. Meier et al.108 compared the differences in Li+ diffusion in tetragonal and cubic phases using a similar technique. In tetragonal LLZO, the Li+ motion is of a fully synchronous collective nature requiring higher activation energy, whereas in cubic LLZO, because of the existence of unoccupied Li sites, the asynchronous collective motion of Li+ caused by single-ion jumps leads to lower activation energy.
As the low-temperature tetragonal LLZO phase has relatively low ionic conductivity, understanding the phase transition mechanism is crucial to stabilizing the high-temperature cubic phase. Using classical MD simulations, Adams et al.109 simulated the phase transition of LLZO. Starting with tetragonal LLZO, a decrease in activation energy is observed when the sample is heated to the phase transition temperature, and the Li ordering vanishes as the temperature further increases. Upon cooling, a tetragonal phase is obtained again but with less structural torsion, and the low activation energy of the high-temperature phase is preserved (Figure 9). Using variable-cell-shape AIMD simulations, Bernstein et al.110 demonstrated that the phase transition temperature of LLZO decreases as the amount of Li vacancies increases because of supervalent ion (e.g., Al3+) doping in the Li sublattice. Various observations that Al doping stabilizes the cubic phase111, 112 can thus be explained by the increased entropy from Li vacancies, which eventually leads to lowering the free energy of cubic LLZO.
Li+ ion conductivities in Li7La3Zr2O12 as derived from mean square displacements of NPT MD (constant temperature, constant pressure molecular dynamic) simulations (NVT MD (constant temperature, constant volume molecular dynamic) simulations in the case of tetragonal samples below 400 K): dark triangles: heating run from tetragonal phase at 273 to 1500 K; light blue triangles: subsequent cooling to 300 K. Overall qualitative trends are in excellent agreement with experimentally measured conductivities (black diamonds and circles). Reproduced with permission from Adams et al.109
There have also been a number of computational studies into doping LLZO to further enhance its conductivity. In general, pentavalent (e.g., Ta5+, Nb5+) ion doping on the Zr sites will stabilize the cubic phase and enhance the ionic conductivity.109, 113, 114 Trivalent dopants (e.g., Ga3+) on either the Li sublattice or La sites can also stabilize the cubic phase,114, 115 but very limited improvement in ionic conductivity is observed for La site doping.114 Using AIMD simulations, Miara et al.113 further demonstrated that the ionic conductivity can be maximized by tuning the dopant (and hence Li) concentration in doped LLZO.
Phosphates and thio-phosphates
As the major component of amorphous thin-film electrolyte LIPON116, crystalline Li3PO4 is of scientific interest despite its low Li+ conductivity. More interesting from the technological application perspective are the thio-phosphates, which encompasses a broad range of materials characterized by the presence of PS43– tetrahedra, with partial substitution of P5+ for aliovalent ions such as Ge4+ or Si4+ for further optimization of the Li+ concentration and conductivity.
Holzwarth et al.117, 118, 119, 120, 121, 122 explored Li+ diffusion in the Li3PO4 and thio-phosphate materials with NEB methods. A general conclusion is that the migration barriers of Li+ in thio-phosphates are much lower than those in phosphates with similar structures (Figure 10), in line with the general intuition that the larger and more polarizable S2– anion promotes higher Li+ mobility.
Nudged elastic band (NEB) energy path diagram for Li ion-vacancy migration in Li4P2S7 and Li4P2O7. The integer labels on the horizontal axis correspond to six vacancy sites. Activation barriers are significantly higher in the oxide than in the sulfide. Reproduced with permission from Holzwarth et al.120
Among the thio-phosphates, the recently discovered Li10GeP2S1222 (LGPS) and Li7P3S11123 have attracted the most excitement because of their extremely high room-temperature Li+ conductivities of >10 mS cm−1, which are comparable to that of organic liquid electrolytes. The first computational study on LGPS was performed by Mo et al.41 using AIMD simulations, and it showed that, contrary to the initial experimental hypothesis, LGPS is in fact an anisotropic 3D conductor rather than a 1D conductor (Figure 11). Similar results were obtained using classical MD simulations40 and NEB calculations.124 In another work, Xu et al.44 revealed the correlation diffusion behavior of Li+ in the 1D channel from AIMD simulations, thus indicating that the low activation energy originates from the strong Coulombic repulsion against neighboring Li+ in the same tube.
Trajectories (white) of Li atoms (green) in ab initio MD (AIMD) simulations of Li10GeP2S12 at 900 K. The one-dimensional diffusion pathway along the c direction (a) and diffusion in the ab plane (b and c). Although the most facile Li diffusion is observed in the c direction, significant diffusion occurs in the a–b plane as well. Reproduced with permission from Mo et al.41
To address two key limitations of LGPS, namely the high costs of Ge and the air and the moisture sensitive nature of sulfide-based chemistry, Ong et al.42 explored the possibility of Li10±1MP2X12 (M=Ge, Si, Sn, Al or P, and X=O, S or Se) for synthesizable solid electrolytes. Isovalent cation substitutions (Si4+ and Sn4+) have a small effect on the Li+ conductivity, but the oxide analogues are unlikely to be stable and have high conductivity. Both Sn125 and Si126 substituted compounds have subsequently been successfully synthesized, and the experimentally measured conductivities are in excellent agreement with the first-principles predictions.
Recently, Wang et al.26 made an interesting observation that both the LGPS and Li7P3S11 superionic conductors, which currently have the highest known Li+ conductivities of any crystal, possess a body-centered cubic system-like sulfur framework. Using NEB calculations, Wang et al.26 showed that the direct transition between tetrahedral sites leads to the lowest activation barrier compared with other transitions in close-packed anion frameworks, such as hcp and fcc (Figure 12). Though this structural feature is rarely observed in known materials, it can serve as a design guideline in developing novel fast superionic conductors.
Li-ion migration pathways in body-centered cubic system/face-centered cubic/hexagonal close-packed (bcc/fcc/hcp)-type anion lattices. (a–c) Li-ion migration path (left panels) and calculated energy path (right panels) in bcc (a), fcc (b) and hcp (c) sulfur lattices. The sulfur anions are colored yellow, and the Li ions are colored green, blue and red for different paths. LiS4 tetrahedra and LiS6 octahedra are colored green and red, respectively. Reproduced with permission from Wang et al.26
For Na-ion chemistry, an exciting new development is the cubic Na3PS4 (c-Na3PS4) solid electrolyte, with conductivities as high as 0.46 mS cm−1 and 0.74 mS cm−1 having been achieved in the undoped and Si-doped materials.127, 128, 129 Using AIMD simulations, Zhu et al.130 showed that the pristine c-Na3PS4 is in fact a poor alkali conductor at room temperature, and it is only with the introduction of Na+ interstitials that the Na+ conductivity approaches the levels observed experimentally. They further proposed Sn doping as a potential strategy to further enhance the conductivity in this material, but this prediction has yet to be verified experimentally.
Li3OX antiperovskites
Inspired by the high-temperature superionic conductivity of Na(K)MgF3 perovskites, Zhao et al.131 proposed a novel family of antiperovskites with the formula Li3OX (X=Cl, Br) as potential solid electrolytes. Zhao et al.131 reported the room temperature ionic conductivities for two samples, 0.85 mS cm−1 for Li3OCl with activation energy of 0.26 eV and 1.94 mS cm−1 for Li3OCl0.5Br0.5 with activation energy of 0.18 eV. The synthetic process strongly indicates that the stoichiometry of the final product deviates from the ideal Li3OX with LiX depletion and Al doping in the structure.
Following the experimental work, Zhang et al.132 proved that Li vacancies and anion sublattice disorder are the driving forces for Li+ diffusion in antiperovskites using AIMD simulations. Emly et al.133 later identified a low-barrier three-atom hopping mechanism involving Li interstitial dumbbells, for which the barriers calculated using NEB methods are ∼170 meV (Figure 13), 50% lower compared with those of vacancy-driven migration. However, defect formation energy calculations suggest that a high Li interstitial concentration can only be obtained by off-stoichiometry synthesis. In an attempt to guide rational optimization of the Cl-Br ratio for maximum Li+ conductivity, Deng et al.134 used NEB calculations to demonstrate that a Cl-rich diffusion channel with Br-rich diffusion end points leads to low-vacancy migration barriers. By combining the NEB barriers within a bond percolation model, Deng et al.134 were able to show that compositions of Li3OCl1−xBrx within 0.235⩽x⩽0.395 are potentially of higher ionic conductivity compared with the antiperovskite compositions that have been synthesized thus far.
(a) Schematic illustration and Li migration barrier in dilute stage II and stage IV diffusion in graphite. (b) Schematic illustration and Li migration barrier under high-concentration conditions in stages I and II. Calculated barriers are highly sensitive to changes in the c lattice parameter. (c) The calculated self-diffusivity for stage I (red) and stage II (blue) in kinetic Monte Carlo (KMC) simulations. Reproduced with permission from Persson et al.135
Anodes
Graphite/graphene-based anodes
Graphite is the most widely used anode material in Li-ion batteries because of its good reversibility and low potential. Persson et al.135, 136 have systematically studied Li diffusion in graphite using a combination of NEB, cluster expansion and KMC methods over a wide range of Li concentrations from x=0.2 to 1.0. The Li intercalation process in graphite is described by multiple stages, where the stage number n indicates n empty layers between each Li-filled graphite layer. NEB calculations were performed to study the in-plane Li vacancy hop at different Li concentrations and lithiation stages. The computation results show that Li diffusion is significantly affected by the different stages and the c-axis spacing of the graphite layers (Figures 13a and b). In addition, strong electrostatic Li–Li repulsion has a significant impact on the Li diffusion at higher Li concentrations. On the basis of the energy barrier of the elementary Li hops, KMC modeling was used to study the Li diffusion at Li concentrations ranging from x=0.2 to 1.0 (stages I and II) and found that Li diffusivity decreases with increasing Li content (Figure 13c). In summary, Li diffusion is fast over the entire range of Li content, in the order of 10−7 to 10−6 cm2 s−1.
In addition, computation studies have shown that the inclusion of van der Waals (vdW) interactions between the graphite layers is important for reproducing experimental results, especially at low Li concentrations. A number of recent studies of Li/Na diffusion in graphitic materials have included the vdW interactions using vdW functionals137, 138, 139 or dispersion corrections.140 The use of vdW functionals significantly improves the agreement with experimental results for alkali (Li, Na, K) diffusion in graphite.
Nanostructured and 2D materials, particularly those based on graphene, have drawn much attention as potential anodes to provide enhanced diffusion. Using NEB calculations, it has been shown that the structure of the graphene edge has a significant impact on Li diffusion and that graphene edges generally show reduced Li diffusion barriers.141 Defects in graphene have also been found to significantly impact the diffusion in numerous DFT studies.142 In particular, defects are critical for having a reasonable barrier for the Li diffusion across the basal plane of the graphene.143, 144 DFT studies have also been performed to investigate the Li diffusion in graphene doped by different elements, such as N or B.145 It has been shown that the dopant types and concentrations have a significant effect on the Li diffusion migration barriers and that the N- and B-doping combined with certain graphene defects may reduce the diffusion barrier.
Silicon and other anodes
Si is a promising Li-ion battery anode candidate because of its significantly higher capacity compared with graphite. However, mechanical failure associated with volume expansion during the lithiation of Si is a critical problem for its application. The study of Li diffusion in a Si anode using atomistic modeling is more challenging because Li alloys, rather than intercalates, with Si. Multiple intermediate phases are formed during the reaction, and these phases are often amorphous. Therefore, the application of the NEB method is often difficult as the diffusion path is usually not known or not as clearly defined as in the intercalation compounds. Qi and co-workers146 applied AIMD simulations to study Li diffusion during the lithiation of Si. Given that the significant strain generated during lithiation may have a significant impact on the diffusion, the coupling between the mechanical stress and the Li diffusion in Si was captured in the modeling study. The authors found that Li atoms diffuse faster in amorphous Si than crystalline Si and that the MD simulations capture the structure evolution, chemomechanical mixing and Si bond-breaking mechanism during lithiation (Figure 14). In addition, computational methods have been used to study the Li diffusion in Si nanostructures by Chan et al.147 They showed that the interstitial tetrahedral sites are energetically stable positions, that the hexagonal sites are the saddle points for the diffusion pathway and that a significant reduction of the diffusion barrier can be found with decreasing nanocrystal size. Similar studies have also been performed on the surface diffusion in other alloying anodes, such as Ge and Sn.148 In addition, Van der Ven et al.149 investigated other alloying anode materials such as Al using KMC methods. They showed that strongly correlated motion exists for Li diffusion in these alloying systems, and they calculated the interdiffusion coefficient of Li over a wide range of compositions.
A snapshot of ab initio MD (AIMD) simulations for Li insertion into (upper) crystalline and (lower) amorphous Si at 1200 K. The structures depict intermediate stages of lithiation. Reproduced with permission from Qi and co-workers146.
Other metal oxides compounds, particularly the titanates, are of interest for anode applications because of their outstanding stability. Ziebarth et al.150 showed that Li diffusion in the spinel Li4Ti5O12 and the rocksalt Li7Ti5O12 have low barriers in the range of 0.3–0.48 and 0.20–0.51 eV, respectively. The diffusion barrier is highly dependent on the chemical environment and the mixed occupancy of some sites, for example, the 16d site occupancy in Li4Ti5O12. DFT computations have also been used to show that Li diffusion in TiO2-B has a low migration barrier of 0.3 and 0.5 eV along the [010] and [001] directions, respectively.151
Interfaces
Interfaces or interphases have critical roles in alkali-ion batteries. However, studies of diffusion at the interfaces/interphases are limited, as the atomistic structures are usually unknown and direct experimental characterizations are difficult.
The solid electrolyte interphase (SEI) is a protecting layer formed on the anode via electrolyte decomposition, mainly during the first cycle. The performance of a rechargeable alkali-ion battery, for example, reversibility, rate capability and safety, is highly dependent on the composition and stability of the SEI.152 Studies of diffusion in the SEI are limited because of the complexity of its chemical composition and microstructure. Recently, Qi et al. applied first-principles techniques to study Li diffusion in the crystalline phases, such as Li2CO3 153 and LiF154, which are commonly found in the SEIs with carbonate solvents and fluoride-based salts. A new Li knock-off mechanism, rather than isolated vacancy hopping, is proposed for Li2CO3, which accounts for the fast Li diffusion in this material.153 By incorporating the atomistic diffusivity in mesoscale diffusion equations, good agreement was achieved with experiments. The diffusion barrier and formation energy of various defects in LiF at different potentials have also been investigated using NEB and other computational methods.154 The ionic conductivity is low (10−28 mS cm−1) for LiF at the anode but is significantly higher (10−9 mS cm−1) at the cathode. Aliovalent doping, such as Mg, was suggested to improve the ionic conductivity of the LiF in the SEI.
Artificially applied interfacial layers have been widely investigated as coating layers for the electrodes. Atomic-layer deposition of Al2O3 has been used to provide ultrathin (a few nm) and uniform coatings. Using DFT methods, Hao et al.155 showed that Li diffusion in Al2O3 through the interstitial mechanism is slow. Jung et al.156 studied Al2O3 lithiation to form amorphous Li-Al2O3 coating layers using AIMD and found that the Li diffusion is significantly enhanced at the lithiated state. Na diffusion has also been investigated in Al2O3. The calculations show that, while the Na insertion into Al2O3 is not favorable, Na exhibits higher diffusivity compared with Li in Al2O3.157
Conclusion and future outlook
The facile conduction of alkali ions is a critical requirement in the predominant form of electrochemical storage today, that is, the rechargeable lithium-ion battery, and energy storage technologies beyond lithium-ion, such as sodium-ion and all-solid-state batteries. An understanding of the chemical and structural factors that support fast alkali ion transport will accelerate the rational design of new materials for energy storage with superior power, rate capability and safety.
Much of this lack in understanding is compounded by the difficulty of accurate experimental investigation of alkali diffusivity. The measured ionic conductivity is affected by a multitude of factors, such as the presence of impurities, grain boundaries and interfaces, which can be difficult to control in a precise manner. Computational techniques, such as those surveyed in this review, are therefore a great complement to experiments. Computational methods provide the means to precisely control the simulation conditions (e.g., modification of a single parameter or set of parameters while keeping other parameters constant), which in turn afford us the ability to conduct a fundamental study of how various structural and chemical factors affect the ionic conductivity.
It is difficult to generalize the insights that have been obtained through the use of computational technique, beyond noting that the factors influencing alkali conductivity are highly structure-dependent. For example, in layered structures, such as the AMO2 cathode and graphite anode,45, 135 it is clear that the interlayer spacing has a substantial effect on the alkali migration barriers, whereas the relationship between alkali ion radii and bottleneck size seems to have a larger role in rigid close-packed anion frameworks (e.g., olivine LiMPO4).11 In addition to migration barriers, the concentration of carriers is another factor contributing to overall ionic conductivity. In this respect, experimental composition scanning is generally still a more rapid mean of determining optimal dopant concentrations because of the inherent difficulty in investigating small concentration changes using computational methods. Nevertheless, there have been recent successes in computational dopant optimizations for solid electrolyte materials.113, 130
Despite significant progress, existing computational methods for probing alkali diffusion—ab initio and classical MDs, transition state theory and kinetic Monte Carlo (KMC)—all suffer from various limitations. Ab initio methods, such as NEB and AIMD, tend to be computationally expensive, whereas methods that depend on empirical or fitted potentials, such as classical MD and KMC, while much cheaper computationally, are difficult to transfer between chemistries and structures. It is interesting to note that the methods and approaches used for different components reflect the fundamental differences in ionic conductivity requirements. Generally, the NEB method is heavily used in the study of all components, but it is more commonly applied to the dilute (fully alkaliated or dealkaliated) limits in electrode materials to understand basic atomistic hopping mechanisms at the beginning of charge or discharge. For especially important materials (e.g., LiCoO2), NEB barriers have been integrated into a KMC model to access non-dilute limits, but this approach is too intensive in terms of human and computational effort as a general strategy for a large number of materials. Alternately, AIMD simulations are more common in solid electrolytes, which usually exhibit alkali disorder and tend to have much higher diffusivities compared with the electrodes. Modeling of electrolyte materials in the dilute limit is generally a poor approximation of diffusion in the non-dilute real material. AIMD simulations of electrode materials have been less common because of the difficulty in obtaining converged statistics because of lower diffusivities.
In the authors’ opinion, the major materials challenges for computational investigations lie beyond bulk crystals and are instead at the interfaces between materials. In many real-world applications, the limiting factor is often the alkali conductivity at either the grain boundaries (e.g., in the LLZO and LLTO solid electrolytes) or the heterogeneous interface between two different materials, such as the electrodes and the electrolyte. Alkali conduction at heterogeneous interfaces is particularly complicated by the reactivity, for example, between Li and most solid electrolytes.
The solutions to these limitations and challenges are multifold. First, computational power will continue to grow, enabling longer simulations and larger system sizes and complexity. Second, multiscale techniques that aim to bridge multiple time and length scales will continue to improve, enhancing our ability to probe ever more realistic models with greater accuracy. Finally, the development of software automation tools will facilitate such investigations. Fundamentally, a key bottleneck in many investigations is not computational expense (which is manageable) but rather the researcher time required to carry out and monitor such calculations. MD simulations present an extreme example, where multiweek runs well in excess of the wall times of most supercomputing resources are typical. A recent trend in computational materials science has been the development of high-throughput infrastructures158, 159, 160, 161, 162 that can perform ‘standardized’ calculations over hundreds to thousands of materials. Such software developments will surely lower the barrier for computational investigations of alkali diffusion.
We are optimistic that, with continued advances in both computational and experimental techniques, rational design of structural frameworks and chemistries for optimal alkali-ion conductivity will soon be within reach. That understanding will not only enhance our ability to develop electrode materials with better cycling stability and higher capacities but also enable the development of next-generation architectures (e.g., all-solid-state batteries) that are safer and more energy-dense than traditional rechargeable lithium-ion batteries.
References
Whittingham, M. S. Electrical energy storage and intercalation chemistry. Science 192, 1126–1127 (1976).
Padhi, A., Nanjundaswamya, K. & Goodenough, J. Phospho-olivines as positive-electrode materials for rechargeable lithium batteries. J. Electrochem. Soc. 144, 1188–1194 (1997).
Mizushima, K., Jones, P. C., Wiseman, P. J. & Goodenough, J. B. LixCoO2 (0<x≤1): a new cathode material for batteries of high energy density. Mater. Res. Bull. 15, 783–789 (1980).
Whittingham, M. S. Lithium batteries and cathode materials. Chem. Rev. 104, 4271–4301 (2004).
Whittingham, M. S. Ultimate limits to intercalation reactions for lithium batteries. Chem. Rev. 114, 11414–11443 (2014).
Whittingham, M. S. Chemistry of intercalation compounds: metal guests in chalcogenide hosts. Prog. Solid State Chem. 12, 41–99 (1978).
Nagelberg, A. S. & Worrell, W. L. A thermodynamic study of sodium-intercalated TaS2 and TiS2 . J. Solid State Chem. 29, 345–354 (1979).
Delmas, C., Braconnier, J., Fouassier, C. & Hagenmuller, P. Electrochemical intercalation of sodium in NaxCoO2 bronzes. Solid State Ionics 3-4, 165–169 (1981).
Zhao, J., He, J., Ding, X., Zhou, J., Ma, Y., Wu, S. & Huang, R. A novel sol–gel synthesis route to NaVPO4F as cathode material for hybrid lithium ion batteries. J. Power Sources 195, 6854–6859 (2010).
Whitacre, J. F., Tevar, A. & Sharma, S. Na4Mn9O18 as a positive electrode material for an aqueous electrolyte sodium-ion energy storage device. Electrochem. Commun. 12, 463–466 (2010).
Ong, S. P., Chevrier, V. L., Hautier, G., Jain, A., Moore, C., Kim, S., Ma, X. & Ceder, G. Voltage, stability and diffusion barrier differences between sodium-ion and lithium-ion intercalation materials. Energy Environ. Sci. 4, 3680–3688 (2011).
Yabuuchi, N., Kajiyama, M., Iwatate, J., Nishikawa, H., Hitomi, S., Okuyama, R., Usui, R., Yamada, Y. & Komaba, S. P2-type Nax[Fe1/2Mn1/2]O2 made from earth-abundant elements for rechargeable Na batteries. Nat. Mater. 11, 512–517 (2012).
McGraw, J., Bahn, C. S., Parilla, P. A., Perkins, J. D., Readey, D. W. & Ginley, D. S. Li ion diffusion measurements in V2O5 and Li(Co1−xAlxO2 thin-film battery cathodes. Electrochim. Acta 45, 187–196 (1999).
Van Der Ven, A. & Ceder, G. Lithium diffusion in layered LixCoO2 . Electrochem. Solid-State Lett. 3, 301–304 (2000).
Jang, Y. -I., Neudecker, B. J. & Dudney, N. J. Lithium diffusion in LixCoO2 (0.45<x<0.7) intercalation cathodes. Electrochem. Solid-State Lett. 4, A74–A77 (2001).
Kang, K., Morgan, D. & Ceder, G. First principles study of Li diffusion in I-Li2NiO2 structure. Phys. Rev. B 79, 014305 (2009).
Morgan, D., Van der Ven, A. & Ceder, G. Li conductivity in LixMPO4 (M=Mn, Fe, Co, Ni) olivine materials. Electrochem. Solid-State Lett. 7, A30–A32 (2004).
Stallworth, P. E., Fontanella, J. J., Wintersgill, M. C., Scheidler, C. D., Immel, J. J., Greenbaum, S. G. & Gozdz, A. S. NMR, DSC and high pressure electrical conductivity studies of liquid and hybrid electrolytes. J. Power Sources 81-82, 739–747 (1999).
Xu, K. Electrolytes and interphases in Li-ion batteries and beyond. Chem. Rev. 114, 11503–11618 (2014).
Stramare, S., Thangadurai, V. & Weppner, W. Lithium lanthanum titanates: a review. Chem. Mater. 15, 3974–3990 (2003).
Knauth, P. Inorganic solid Li ion conductors: an overview. Solid State Ionics 180, 911–916 (2009).
Kamaya, N., Homma, K., Yamakawa, Y., Hirayama, M., Kanno, R., Yonemura, M., Kamiyama, T., Kato, Y., Hama, S., Kawamoto, K. & Mitsui, A. A lithium superionic conductor. Nat. Mater. 10, 682–686 (2011).
Goodenough, J. B., Hong, H. Y. -P. & Kafalas, J. A. Fast Na+-ion transport in skeleton structures. Mater. Res. Bull. 11, 203–220 (1976).
Jalem, R., Yamamoto, Y., Shiiba, H., Nakayama, M., Munakata, H., Kasuga, T. & Kanamura, K. Concerted migration mechanism in the Li ion dynamics of Garnet-type Li7La3Zr2O12 . Chem. Mater. 25, 425–430 (2011).
Kanno, R., Hata, T., Kawamoto, Y. & Irie, M. Synthesis of a new lithium ionic conductor, thio-LISICON—lithium germanium sulfide system. Solid State Ionics 130, 97–104 (2000).
Wang, Y., Richards, W. D., Ong, S. P., Miara, L. J., Kim, J. C., Mo, Y. & Ceder, G. Design principles for solid-state lithium superionic conductors. Nat. Mater. 14, 1026–1031 (2015).
Hong, H. Y. -P. Crystal structures and crystal chemistry in the system Na1+xZr2SixP3−xO12 . Mater. Res. Bull. 11, 173–182 (1976).
Delmas, C., Fouassier, C. & Hagenmuller, P. Structural classification and properties of the layered oxides. Phys. B+C 99, 81–85 (1980).
Mo, Y., Ong, S. P. & Ceder, G. Insights into diffusion mechanisms in P2 layered oxide materials by first-principles calculations. Chem. Mater. 26, 5208–5214 (2014).
Ceder, G., Hautier, G., Jain, A. & Ong, S. P. Recharging lithium battery research with first-principles methods. MRS Bull. 36, 185–191 (2011).
Xu, B., Qian, D., Wang, Z. & Meng, Y. S. Recent progress in cathode materials research for advanced lithium ion batteries. Mater. Sci. Eng. R 73, 51–65 (2012).
Meng, Y. S. & Dompablo, M. E. A. Computational research of cathode materials for lithium-ion batteries. Acc. Chem. Res. 46, 1171–1180 (2013).
Islam, M. S. & Fisher, C. A. J. Lithium and sodium battery cathode materials: computational insights into voltage, diffusion and nanostructural properties. Chem. Soc. Rev. 43, 185–204 (2014).
Glicksman, M. E. Diffusion in Solids: Field Theory, Solid-State Principles, and Applications, (Wiley-Interscience, 1999).
Balluffi, R. W., Allen, S. M. & Carter, W. C. Kinetics of Materials, (Wiley-Interscience, 2005).
Vineyard, G. H. Frequency factors and isotope effects in solid state rate processes. J. Phys. Chem. Solids 3, 121–127 (1957).
Jonsson, H., Mills, G. & Jacobsen, K. W. in Classical and Quantum Dynamics in Condensed Phase Simulations—Proceedings of the International School of Physics, (World Scientific Publishing, 1998) doi:10.1142/9789812839664_0016.
Van Der Ven, A. First Principles Investigation of the Thermydynamic and Kinetic Properties of Lithium Transition Metal Oxides, (Massachusetts Institute of Technology, 2000).
Pedone, A., Malavasi, G., Menziani, M. C., Cormack, A. N. & Segre, U. Article a new self-consistent empirical interatomic potential model for oxides, silicates, and silica-based glasses a new self-consistent empirical interatomic potential model for oxides, silicates, and silica-based glasses. J. Phys. Chem. B 110, 11780–11795 (2006).
Adams, S. & Rao, R. P. Structural requirements for fast lithium ion migration in Li10GeP2S12 . J. Mater. Chem. 22, 7687–7691 (2012).
Mo, Y., Ong, S. P. & Ceder, G. First principles study of the Li10GeP2S12 lithium super ionic conductor material. Chem. Mater. 24, 15–17 (2012).
Ong, S. P., Mo, Y., Richards, W. D., Miara, L., Lee, H. S. & Ceder, G. Phase stability, electrochemical stability and ionic conductivity of the Li10±1MP2X12M=Ge, Si, Sn, Al or P, and X=O, S or Se) family of superionic conductors. Energy Environ. Sci 6, 148–156 (2013).
Car, R. & Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 55, 2471–2474 (1985).
Xu, M., Ding, J. & Ma, E. One-dimensional stringlike cooperative migration of lithium ions in an ultrafast ionic conductor. Appl. Phys. Lett. 101, 031901 (2012).
Kang, K., Meng, Y. S., Bréger, J., Grey, C. P. & Ceder, G. Electrodes with high power and high capacity for rechargeable lithium batteries. Science 311, 977–980 (2006).
Mortemard de Boisse, B., Carlier, D., Guignard, M. & Delmas, C. Structural and electrochemical characterizations of P2 and new O3-NaxMn1-yFeyO2 phases prepared by auto-combustion synthesis for na-ion batteries. J. Electrochem. Soc. 160, A569–A574 (2013).
Ammundsen, B., Rozière, J. & Islam, M. S. Atomistic simulation studies of lithium and proton insertion in spinel lithium manganates. J. Phys. Chem. B 101, 8156–8163 (1997).
Ouyang, C. Y., Shi, S. Q., Wang, Z. X., Li, H., Huang, X. J. & Chen, L. Q. Ab initio molecular-dynamics studies on LixMn2O4 as cathode material for lithium secondary batteries. Europhys. Lett. 67, 28–34 (2004).
Xu, B. & Meng, S. Factors affecting Li mobility in spinel LiMn2O4—a first-principles study by GGA and GGA+U methods. J. Power Sources 195, 4971–4976 (2010).
Yang, M. -C., Xu, B., Cheng, J. -H., Pan, C. -J., Hwang, B. -J. & Meng, Y. S. Electronic, structural, and electrochemical properties of LiNixCuyMn2–x–yO 4 (0<x<0.5, 0<y<0.5) high-voltage spinel materials. Chem. Mater. 23, 2832–2841 (2011).
Nakayama, M., Kaneko, M. & Wakihara, M. First-principles study of lithium ion migration in lithium transition metal oxides with spinel structure. Phys. Chem. Chem. Phys. 14, 13963–13970 (2012).
Ling, C. & Mizuno, F. Phase stability of post-spinel compound AMn2O4 (A=Li, Na, or Mg) and its application as a rechargeable battery cathode. Chem. Mater. 25, 3062–3071 (2013).
Hewston, T. A. & Chamberland, B. L. A survey of first-row ternary oxides LiMO2 (M=Sc-Cu). J. Phys. Chem. Solids 48, 97–108 (1987).
Urban, A., Lee, J. & Ceder, G. The configurational space of rocksalt-type oxides for high-capacity lithium battery electrodes. Adv. Energy Mater. 4, 1400478 (2014).
Lee, J., Urban, A., Li, X., Su, D., Hautier, G. & Ceder, G. Unlocking the potential of cation-disordered oxides for rechargeable lithium batteries. Science 343, 519–522 (2014).
Hautier, G., Jain, A., Ong, S. P., Kang, B., Moore, C., Doe, R. & Ceder, G. Phosphates as lithium-ion battery cathodes: an evaluation based on high-throughput ab initio calculations. Chem. Mater. 23, 3495–3508 (2011).
Islam, M. S., Driscoll, D. J., Fisher, C. A. J. & Slater, P. R. Atomic-scale investigation of defects, dopants, and lithium transport in the LiFePO4 Olivine-type battery material. Chem. Mater. 17, 5085–5092 (2005).
Malik, R., Burch, D., Bazant, M. & Ceder, G. Particle size dependence of the ionic diffusivity. Nano Lett. 10, 4123–4127 (2010).
Moreau, P., Guyomard, D., Gaubicher, J. & Boucher, F. Structure and stability of sodium intercalated phases in olivine FePO4 . Chem. Mater. 22, 4126–4128 (2010).
Zaghib, K., Trottier, J., Hovington, P., Brochu, F., Guerfi, A., Mauger, A. & Julien, C. M. Characterization of Na-based phosphate as electrode materials for electrochemical cells. J. Power Sources 196, 9612–9617 (2011).
Oh, S. -M., Myung, S. -T., Hassoun, J., Scrosati, B. & Sun, Y. -K. Reversible NaFePO4 electrode for sodium secondary batteries. Electrochem. Commun. 22, 149–152 (2012).
Bridson, J. N., Quinlan, S. E. & Tremaine, P. R. Synthesis and crystal structure of maricite and sodium iron(III) hydroxyphosphate. Chem. Mater. 10, 763–768 (1998).
Tripathi, R., Wood, S. M., Islam, M. S. & Nazar, L. F. Na-ion mobility in layered Na2FePO4F and olivine Na[Fe,Mn]PO4 . Energy Environ. Sci. 6, 2257–2264 (2013).
Tamaru, M., Chung, S. -C., Shimizu, D., Nishimura, S. & Yamada, A. Pyrophosphate chemistry toward safe rechargeable batteries. Chem. Mater. 25, 2538–2543 (2013).
Barpanda, P., Nishimura, S. & Yamada, A. High-voltage pyrophosphate cathodes. Adv. Energy Mater. 2, 841–859 (2012).
Kim, H. H., Lee, S., Park, Y. -U., Kim, J., Jeon, S. & Kang, K. Neutron and X-ray diffraction study of pyrophosphate-based Li2–x MP2O7M=Fe, Co) for lithium rechargeable battery electrodes. Chem. Mater. 23, 3930–3937 (2011).
Kim, H., Park, I., Seo, D. -H., Lee, S., Kim, S. -W., Kwon, W. J., Park, Y.-U., Kim, C. S., Jeon, S. & Kang, K. New iron-based mixed-polyanion cathodes for lithium and sodium rechargeable batteries: combined first principles calculations and experimental study. J. Am. Chem. Soc. 134, 10369–10372 (2012).
Clark, J. M., Nishimura, S., Yamada, A. & Islam, M. S. High-voltage pyrophosphate cathode: insights into local structure and lithium-diffusion pathways. Angew. Chem. Int. Ed. 51, 13149–13153 (2012).
Kerr, T. A., Gaubicher, J. & Nazar, L. F. Highly reversible Li insertion at 4V in ɛ-VOPO4/α-LiVOPO4 cathodes. Electrochem. Solid-State Lett. 3, 460–462 (2000).
Barker, J., Saidi, M. Y. & Swoyer, J. L. Electrochemical insertion properties of the novel lithium vanadium fluorophosphate, LiVPO4F. J. Electrochem. Soc. 150, A1394–A1398 (2003).
Barker, J., Gover, R. K. B., Burns, P. & Bryan, A. A symmetrical lithium-ion cell based on lithium vanadium fluorophosphate, LiVPO4F. Electrochem. Solid-State Lett. 8, A285–A287 (2005).
Barker, J., Gover, R. K. B., Burns, P., Bryan, A., Saidi, M. Y. & Swoyer, J. L. Structural and electrochemical properties of lithium vanadium fluorophosphate, LiVPO4F. J. Power Sources 146, 516–520 (2005).
Gover, R. K. B., Burns, P., Bryan, A., Saidi, M. Y., Swoyer, J. L. & Barker, J. LiVPO4F: a new active material for safe lithium-ion batteries. Solid State Ionics 177, 2635–2638 (2006).
Mueller, T., Hautier, G., Jain, A. & Ceder, G. Evaluation of tavorite-structured cathode materials for lithium-ion batteries using high-throughput computing. Chem. Mater. 23, 3854–3862 (2011).
Ling, C., Zhang, R. & Mizuno, F. Phase stability and its impact on the electrochemical performance of VOPO4 and LiVOPO4 . J. Mater. Chem. A 2, 12330–12339 (2014).
Chen, Z., Chen, Q., Wang, H., Zhang, R., Zhou, H., Chen, L. & Whittingham, M. S. A β-VOPO4/ɛ-VOPO4 composite Li-ion battery cathode. Electrochem. Commun. 46, 67–70 (2014).
Azmi, B. M., Ishihara, T., Nishiguchi, H. & Takita, Y. Cathodic performance of VOPO4 with various crystal phases for Li ion rechargeable battery. Electrochim. Acta 48, 165–170 (2002).
Azmi, B. M., Ishihara, T., Nishiguchi, H. & Takita, Y. Vanadyl phosphates of VOPO4 as a cathode of Li-ion rechargeable batteries. J. Power Sources 119-121, 273–277 (2003).
Dupré, N., Gaubicher, J., Le Mercier, T., Wallez, G., Angenault, J. & Quarton, M. Positive electrode materials for lithium batteries based on VOPO4 . Solid State Ionics 140, 209–221 (2001).
Dupré, N., Wallez, G., Gaubicher, J. & Quarton, M. Phase transition induced by lithium insertion in αI- and αII-VOPO4 . J. Solid State Chem. 177, 2896–2902 (2004).
Harrison, K. L., Bridges, C. A., Segre, C. U., Varnado, C. D., Applestone, D., Bielawski, C. W., Paranthaman, M. P. & Manthiram, A. Chemical and electrochemical lithiation of LiVOPO4 cathodes for lithium-ion batteries. Chem. Mater. 26, 3849–3861 (2014).
Harrison, K. L. & Manthiram, A. Microwave-assisted solvothermal synthesis and characterization of various polymorphs of LiVOPO4 . Chem. Mater. 25, 1751–1760 (2013).
Song, Y., Zavalij, P. Y. & Whittingham, M. S. ɛ-VOPO4: electrochemical synthesis and enhanced cathode behavior. J. Electrochem. Soc. 152, A721–A728 (2005).
Adams, S. & Rao, R. P. Simulated defect and interface engineering for high power Li electrode materials. Solid State Ionics 184, 57–61 (2011).
Ramzan, M., Lebègue, S., Kang, T. W. & Ahuja, R. Hybrid density functional calculations and molecular dynamics study of lithium fluorosulphate, a cathode material for lithium-ion batteries. J. Phys. Chem. C 115, 2600–2603 (2011).
Liivat, A. & Thomas, J. O. Li-ion migration in Li2FeSiO4-related cathode materials: A DFT study. Solid State Ionics 192, 58–64 (2011).
Liivat, A. Structural changes on cycling Li2FeSiO4 polymorphs from DFT calculations. Solid State Ionics 228, 19–24 (2012).
Wu, S. Q., Zhu, Z. Z., Yang, Y. & Hou, Z. F. Structural stabilities, electronic structures and lithium deintercalation in Lix MSiO4 (M=Mn, Fe, Co, Ni): A GGA and GGA+U study. Comput. Mater. Sci. 44, 1243–1251 (2009).
Arroyo-de Dompablo, M. E., Armand, M., Tarascon, J. M. & Amador, U. On-demand design of polyoxianionic cathode materials based on electronegativity correlations: An exploration of the Li2MSiO4 system (M=Fe, Mn, Co, Ni). Electrochem. Commun. 8, 1292–1298 (2006).
Su, D., Ahn, H. & Wang, G. Ab initio calculations on Li-ion migration in Li2FeSiO4 cathode material with a P21 symmetry structure. Appl. Phys. Lett. 99, 141909 (2011).
Saracibar, A., Van der Ven, A. & Arroyo-de Dompablo, M. E. Crystal structure, energetics, and electrochemistry of Li2FeSiO4 polymorphs from first principles calculations. Chem. Mater. 24, 495–503 (2012).
Eames, C., Armstrong, A. R., Bruce, P. G. & Islam, M. S. Insights into changes in voltage and structure of Li2FeSiO4 polymorphs for lithium-ion batteries. Chem. Mater. 24, 2155–2161 (2012).
Arroyo-de Dompablo, M. E., Dominko, R., Gallardo-Amores, J. M., Dupont, L., Mali, G., Ehrenberg, H., Jamnik, J. & Morán, E. On the energetic stability and electrochemistry of Li2MnSiO4 polymorphs. Chem. Mater. 20, 5574–5584 (2008).
Longo, R. C., Xiong, K. & Cho, K. Multicomponent silicate cathode materials for rechargeable Li-ion batteries: an ab initio study. J. Electrochem. Soc. 160, A60–A65 (2013).
Seo, D. -H., Kim, H., Park, I., Hong, J. & Kang, K. Polymorphism and phase transformations of Li2−xFeSiO4 (0≤x≤2) from first principles. Phys. Rev. B 84, 220106 (2011).
Kuganathan, N. & Islam, M. S. Li2MnSiO4 lithium battery material: atomic-scale study of defects, lithium mobility, and trivalent dopants. Chem. Mater. 21, 5196–5202 (2009).
Kumar, P. P. & Yashonath, S. A full interionic potential for Na1+xZr2SixP3–xO12 superionic conductors. J. Am. Chem. Soc. 124, 3828–3829 (2002).
Kumar, P. P. & Yashonath, S. Structure, conductivity, and ionic motion in Na1+xZr2SixP3–xO12: a simulation study. J. Phys. Chem. B 106, 7081–7089 (2002).
Lang, B., Ziebarth, B. & Elsässer, C. Lithium ion conduction in LiTi2(PO4)3 and related compounds based on the NASICON structure: a first-principles study. Chem. Mater. 27, 5040–5048 (2015).
Inaguma, Y., Liquan, C., Itoh, M., Nakamura, T., Uchida, T., Ikuta, H. & Wakihara, M. High ionic conductivity in lithium lanthanum titanate. Solid State Commun. 86, 689–693 (1993).
Catti, M. First-principles modeling of lithium ordering in the LLTO (LixLa2/3–x/3TiO3) superionic conductor. Chem. Mater. 19, 3963–3972 (2007).
Catti, M. Local structure of the Li1/8La5/8TiO3 (LLTO) ionic conductor by theoretical simulations. J. Phys. Conf. Ser. 117, 012008 (2008).
Catti, M. Ion Mobility pathways of the Li+ conductor Li0.125La0.625TiO3 by ab initio simulations. J. Phys. Chem. C 112, 11068–11074 (2008).
Catti, M. Short-range order and Li+ ion diffusion mechanisms in Li5La9□2(TiO3 )16 (LLTO). Solid State Ionics 183, 1–6 (2011).
Moriwake, H., Gao, X., Kuwabara, A., Fisher, C. A. J., Kimura, T., Ikuhara, Y. H., Kohama, K., Tojigamori, T. & Ikuhara, Y. Domain boundaries and their influence on Li migration in solid-state electrolyte (La,Li)TiO3 . J. Power Sources 276, 203–207 (2015).
Murugan, R., Thangadurai, V. & Weppner, W. Fast lithium ion conduction in Garnet-type Li7La3Zr2O12 . Angew. Chemie Int. Ed. 46, 7778–7781 (2007).
Awaka, J., Kijima, N., Hayakawa, H. & Akimoto, J. Synthesis and structure analysis of tetragonal Li7La3Zr2O12 with the garnet-related type structure. J. Solid State Chem. 182, 2046–2052 (2009).
Meier, K., Laino, T. & Curioni, A. Solid-state electrolytes: revealing the mechanisms of Li-ion conduction in tetragonal and cubic LLZO by first-principles calculations. J. Phys. Chem. C 118, 6668–6679 (2014).
Adams, S. & Rao, R. P. Ion transport and phase transition in Li7−xLa3(Zr2−xMxO12M=Ta5+, Nb5+x=0, 0.25). J. Mater. Chem. 22, 1426–1434 (2012).
Bernstein, N., Johannes, M. & Hoang, K. Origin of the structural phase transition in Li7La3Zr2O12 . Phys. Rev. Lett. 109, 205702 (2012).
Geiger, C. A., Alekseev, E., Lazic, B., Fisch, M., Armbruster, T., Langner, R., Fechtelkord, M., Kim, N., Pettke, T. & Weppner, W. Crystal chemistry and stability of ‘Li7La3Zr2O12’ garnet: a fast lithium-ion conductor. Inorg. Chem. 50, 1089–1097 (2011).
Buschmann, H., Dölle, J., Berendts, S., Kuhn, A., Bottke, P., Wilkening, M., Heitjans, P., Senyshyn, A., Ehrenberg, H., Lotnyk, A., Duppel, V., Kienle, L. & Janek, J. Structure and dynamics of the fast lithium ion conductor ‘Li7La3Zr2O12’. Phys. Chem. Chem. Phys. 13, 19378–19392 (2011).
Miara, L. J., Ong, S. P., Mo, Y., Richards, W. D., Park, Y., Lee, J. -M., Lee, H. S. & Ceder, G. Effect of Rb and Ta doping on the ionic conductivity and stability of the garnet Li7+2x–y(La3–xRbx)(Zr2–y Tay)O12 (0≤x≤0.375, 0≤y≤1) superionic conductor: a first principles investigation. Chem. Mater. 25, 3048–3055 (2013).
Gu, W., Ezbiri, M., Rao, R. P., Avdeev, M. & Adams, S. Effects of penta- and trivalent dopants on structure and conductivity of Li7La3Zr2O12 . Solid State Ionics 274, 100–105 (2015).
Jalem, R., Rushton, M., Manalastas, W., Nakayama, M., Kasuga, T., Kilner, J. A. & Grimes, R. W. Effects of gallium doping in garnet-type Li7La3Zr2O12 solid electrolytes. Chem. Mater. 27, 2821–2831 (2015).
Dudney, N. J. Solid-state thin-film rechargeable batteries. Mater. Sci. Eng. B 116, 245–249 (2005).
Du, Y. A. & Holzwarth, N. A. W. Li ion diffusion mechanisms in the crystalline electrolyte γ-Li3PO4 . J. Electrochem. Soc. 154, A999–A1004 (2007).
Du, Y. A. & Holzwarth, N. A. W. Mechanisms of Li+ diffusion in crystalline γ- and β-Li3P O4 electrolytes from first principles. Phys. Rev. B 76, 174302 (2007).
Du, Y. A. & Holzwarth, N. A. W. Effects of O vacancies and N or Si substitutions on Li+ migration in Li3PO4 electrolytes from first principles. Phys. Rev. B 78, 174301 (2008).
Holzwarth, N. A. W., Lepley, N. D. & Du, Y. A. Computer modeling of lithium phosphate and thiophosphate electrolyte materials. J. Power Sources 196, 6870–6876 (2011).
Lepley, N. D. & Holzwarth, N. A. W. Computer modeling of crystalline electrolytes: lithium thiophosphates and phosphates. J. Electrochem. Soc. 159, A538–A547 (2012).
Lepley, N. D., Holzwarth, N. A. W. & Du, Y. A. Structures, Li+ mobilities, and interfacial properties of solid electrolytes Li3PS4 and Li3PO4 from first principles. Phys. Rev. B 88, 104103 (2013).
Seino, Y., Ota, T., Takada, K., Hayashi, A. & Tatsumisago, M. A sulphide lithium super ion conductor is superior to liquid ion conductors for use in rechargeable batteries. Energy Environ. Sci 7, 627–631 (2014).
Du, F., Ren, X., Yang, J., Liu, J. & Zhang, W. Structures, thermodynamics, and Li+ mobility of Li10GeP2S12: a first-principles analysis. J. Phys. Chem. C 118, 10590–10595 (2014).
Bron, P., Johansson, S., Zick, K., Der Günne, J. S. A., Dehnen, S. & Roling, B. Li10SnP2S12: an affordable lithium superionic conductor. J. Am. Chem. Soc. 135, 15694–15697 (2013).
Kuhn, A., Gerbig, O., Zhu, C., Falkenberg, F., Maier, J. & Lotsch, B. V. A new ultrafast superionic Li-conductor: ion dynamics in Li11Si2PS12 and comparison with other tetragonal LGPS-type electrolytes. Phys. Chem. Chem. Phys. 16, 14669–14674 (2014).
Hayashi, A., Noi, K., Sakuda, A. & Tatsumisago, M. Superionic glass-ceramic electrolytes for room-temperature rechargeable sodium batteries. Nat. Commun. 3, 856 (2012).
Hayashi, A., Noi, K., Tanibata, N., Nagao, M. & Tatsumisago, M. High sodium ion conductivity of glass–ceramic electrolytes with cubic Na3PS4 . J. Power Sources 258, 420–423 (2014).
Tanibata, N., Noi, K., Hayashi, A. & Tatsumisago, M. Preparation and characterization of highly sodium ion conducting Na3PS4–Na4SiS4 solid electrolytes. RSC Adv. 4, 17120–17123 (2014).
Zhu, Z., Chu, I. -H., Deng, Z. & Ong, S. P. Role of Na+ interstitials and dopants in enhancing the Na+ conductivity of the cubic Na3PS4 superionic conductor. Chem. Mater. 27, 8318–8325 (2015).
Zhao, Y. & Daemen, L. L. Superionic conductivity in lithium-rich anti-perovskites. J. Am. Chem. Soc. 134, 15042–15047 (2012).
Zhang, Y., Zhao, Y. & Chen, C. Ab initio study of the stabilities of and mechanism of superionic transport in lithium-rich antiperovskites. Phys. Rev. B 87, 134303 (2013).
Emly, A., Kioupakis, E. & Van der Ven, A. Phase stability and transport mechanisms in antiperovskite Li3OCl and Li3OBr superionic conductors. Chem. Mater. 25, 4663–4670 (2013).
Deng, Z., Radhakrishnan, B. & Ong, S. P. Rational composition optimization of the lithium-Rich Li3OCl1–xBrx anti-perovskite superionic conductors. Chem. Mater. 27, 3749–3755 (2015).
Persson, K., Hinuma, Y., Meng, Y. S., Van der Ven, A. & Ceder, G. Thermodynamic and kinetic properties of the Li-graphite system from first-principles calculations. Phys. Rev. B 82, 125416 (2010).
Persson, K., Sethuraman, V. A., Hardwick, L. J., Hinuma, Y., Meng, Y. S., Van Der Ven, A., Srinivasan, V., Kostecki, R. & Ceder, G. Lithium diffusion in graphitic carbon. J. Phys. Chem. Lett. 1, 1176–1180 (2010).
Wang, Z., Selbach, S. M. & Grande, T. Van der Waals density functional study of the energetics of alkali metal intercalation in graphite. RSC Adv. 4, 4069–4079 (2014).
Wang, Z., Ratvik, A. P., Grande, T. & Selbach, S. M. Diffusion of alkali metals in the first stage graphite intercalation compounds by vdW-DFT calculations. RSC Adv. 5, 15985–15992 (2015).
Ganesh, P., Kim, J., Park, C., Yoon, M., Reboredo, F. A. & Kent, P. R. C. Binding and diffusion of lithium in graphite: quantum monte carlo benchmarks and validation of van der Waals density functional methods. J. Chem. Theory Comput. 10, 5318–5323 (2014).
Thinius, S., Islam, M. M., Heitjans, P. & Bredow, T. Theoretical study of Li migration in lithium-graphite intercalation compounds with dispersion-corrected DFT methods. J. Phys. Chem. C 118, 2273–2280 (2014).
Uthaisar, C. & Barone, V. Edge effects on the characteristics of Li diffusion in graphene. Nano Lett. 10, 2838–2842 (2010).
Zhou, L. -J., Hou, Z. F. & Wu, L. -M. First-principles study of lithium adsorption and diffusion on graphene with point defects. J. Phys. Chem. C 116, 21780–21787 (2012).
Yao, F., Güneş, F., Ta, H. Q., Lee, S. M., Chae, S. J., Sheem, K. Y., Cojocaru, C. S., Xie, S. S. & Lee, Y. H. Diffusion mechanism of lithium ion through basal plane of layered graphene. J. Am. Chem. Soc. 134, 8646–8654 (2012).
Fan, X., Zheng, W. T. & Kuo, J. -L. Adsorption and diffusion of li on pristine and defective graphene. ACS Appl. Mater. Interfaces 4, 2432–2438 (2012).
Das, D., Kim, S., Lee, K. -R. & Singh, A. K. Li diffusion through doped and defected graphene. Phys. Chem. Chem. Phys. 15, 15128–15134 (2013).
Johari, P., Qi, Y. & Shenoy, V. B. The mixing mechanism during lithiation of Si negative electrode in Li-ion batteries: an ab initio molecular dynamics study. Nano Lett. 11, 5494–5500 (2011).
Chan, T. -L. & Chelikowsky, J. R. Controlling diffusion of lithium in silicon nanostructures. Nano Lett. 10, 821–825 (2010).
Jung, S. C. & Han, Y. -K. Lithium intercalation behaviors in Ge and Sn crystalline surfaces. Phys. Chem. Chem. Phys. 15, 13586–13592 (2013).
Van der Ven, A. & Ceder, G. First principles calculation of the interdiffusion coefficient in binary alloys. Phys. Rev. Lett. 94, 045901 (2005).
Ziebarth, B., Klinsmann, M., Eckl, T. & Elsässer, C. Lithium diffusion in the spinel phase Li4Ti5O12 and in the rocksalt phase Li7Ti5O12 of lithium titanate from first principles. Phys. Rev. B 89, 174301 (2014).
Arrouvel, C., Parker, S. C. & Islam, M. S. Lithium insertion and transport in the TiO2-B anode material: a computational study. Chem. Mater. 21, 4778–4783 (2009).
Verma, P., Maire, P. & Novák, P. A review of the features and analyses of the solid electrolyte interphase in Li-ion batteries. Electrochim. Acta 55, 6332–6341 (2010).
Shi, S., Lu, P., Liu, Z., Qi, Y., Hector, L. G., Li, H. & Harris, SJ Direct calculation of Li-ion transport in the solid electrolyte interphase. J. Am. Chem. Soc. 134, 15476–15487 (2012).
Pan, J., Cheng, Y. -T. & Qi, Y. General method to predict voltage-dependent ionic conduction in a solid electrolyte. Phys. Rev. B 91, 134116 (2015).
Hao, S. & Wolverton, C. Lithium transport in amorphous Al2O3 and AlF3 for discovery of battery coatings. J. Phys. Chem. C 117, 8009–8013 (2013).
Jung, S. C. & Han, Y. -K. How do Li atoms pass through the Al2O3 coating layer during lithiation in Li-ion batteries? J. Phys. Chem. Lett. 4, 2681–2685 (2013).
Jung, S. C., Kim, H. -J., Choi, J. W. & Han, Y. -K. Sodium ion diffusion in Al2O3: a distinct perspective compared with lithium ion diffusion. Nano Lett. 14, 6559–6563 (2014).
Jain, A., Hautier, G., Moore, C. J., Ong, S. P., Fischer, C. C., Mueller, T., Persson, K. A. & Ceder, G. A high-throughput infrastructure for density functional theory calculations. Comput. Mater. Sci. 50, 2295–2310 (2011).
Jain, A., Ong, S. P., Chen, W., Medasani, B., Qu, X., Kocher, M., Brafman, M., Petretto, G., Rignanese, G.-M., Hautier, G., Gunter, D. & Persson, K. A. FireWorks: a dynamic workflow system designed for high-throughput applications. Concurr. Comput. Pract. Exp. 27, 5037–5059 (2015).
Ong, S. P., Richards, W. D., Jain, A., Hautier, G., Kocher, M., Cholia, S., Gunter, D., Chevrier, V. L., Persson, K. A. & Ceder, G. Python materials genomics (pymatgen): a robust, open-source python library for materials analysis. Comput. Mater. Sci. 68, 314–319 (2013).
Qu, X., Jain, A., Rajput, N. N., Cheng, L., Zhang, Y., Ong, S. P., Brafman, M., Maginn, E., Curtiss, L. A. & Persson, K. A. The electrolyte genome project: a big data approach in battery materials discovery. Comput. Mater. Sci. 103, 56–67 (2015).
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., Gunter, D., Skinner, D., Ceder, G. & Persson, K. A. Commentary: The Materials Project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Acknowledgements
This work was supported by the US Department of Energy, Office of Science, Basic Energy Sciences under Award Number DE-SC0012118.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Deng, Z., Mo, Y. & Ong, S. Computational studies of solid-state alkali conduction in rechargeable alkali-ion batteries. NPG Asia Mater 8, e254 (2016). https://doi.org/10.1038/am.2016.7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/am.2016.7
This article is cited by
-
Designing All-Solid-State Batteries by Theoretical Computation: A Review
Electrochemical Energy Reviews (2023)
-
Emerging Atomic Layer Deposition for the Development of High-Performance Lithium-Ion Batteries
Electrochemical Energy Reviews (2023)
-
Partially delocalized numerical simulation on the conductivity behavior of non-dense solid electrolytes
Ionics (2022)
-
Garnet-type solid electrolyte: Advances of ionic transport performance and its application in all-solid-state batteries
Journal of Advanced Ceramics (2021)
-
Statistical variances of diffusional properties from ab initio molecular dynamics simulations
npj Computational Materials (2018)