Abstract
The discovery of two-dimensional electron gas states with giant Rashba spin splitting (RSS) in electron-doped three-dimensional topological insulators (TIs) uncovered new fascinating physics and raised hopes for novel spintronic devices. Significant challenges, including synthetic constraints and control of the magnetic properties, must be addressed before any breakthroughs are possible. Here, we show how RSS in Bi-rich Bi2Se3 nanoplatelets is responsible for the appearance of remarkable orbital magnetic properties, as observed using magnetization and conduction electron spin resonance experiments and confirmed by theoretical simulations. In view of the strong spin-orbit coupling (SOC) and the proximity to the TI surface states, this discovery enlightens fundamental aspects of SOC-based functionalities of TI materials with aims for future applications.
Similar content being viewed by others
Introduction
Topological insulator (TI) systems represent an unconventional quantum phase of matter controlled by spin-orbit coupling (SOC) with insulating bulk states and gapless metallic surface states.1, 2, 3 Exemplary three-dimensional (3D) TI systems are the group V Bi1−xSbx insulating alloys4 and the group V–VI chalcogenide materials Bi2Se3, Bi2Te3 and Sb2Te3.1, 2, 5 The distinct properties of TI surface electron states appear attractive for fundamental research as well as for spintronic,6, 7 quantum information8 and low-energy dissipation electronic applications.9 For spintronics, controlling the surface electronic properties of TIs requires interfacing with other materials;10 this may generate strong energy changes (bending) in the electron bands near the interface. Adsorbents, defects and stoichiometric deficiencies cause electron doping and strong bending of the electron bands.11 In the case of Bi2Se3, experiments have shown that strong electron doping induced by Bi intercalation, Se vacancies and BiSe antisite defects is unavoidable12 and leads to the surface transport properties being obscured by the bulk conductivity.13
Angle-resolved photoemission spectroscopy studies of Bi2Se3 have shown that band bending gives rise to two-dimensional electron gas (2DEG) states with a band bottom at the Γ point of the Brillouin zone, which coexist with the TI surface states.14 By increasing bending, the 2DEG band bottom shifts symmetrically away from the Γ point, indicating the formation of Rashba spin-orbit splitting.15, 16 The relevant Fermi surface consists of two concentric Fermi subsurfaces with opposite spin directions and is similar to the one observed in Au(1 1 1).17, 18, 19 Remarkably, the Rashba parameter αR for Bi2Se3 acquires an extraordinarily large value (αR≈0.79 eVÅ) that is an order of magnitude greater than that for semiconducting 2DEGs and more than two times the Rashba parameter for Au(1 1 1) (αR≈0.33 eVÅ).15, 16 The question is thus whether Bi2Se3 attains a noticeable orbital magnetism (OM) in a manner similar to gold nanostructures20 or the giant Rashba semiconductor BiTeI.21 In ordinary crystalline materials, OM is typically quenched because of the reduced crystal symmetry. For example, in the case of Ni, Co and Fe, the OM is only a few percent of the total magnetization.22 However, in systems with topologically nontrivial band structures, a large OM is expected on electron states near the Dirac point.23 Similarly, theoretical and experimental work on strong Rashba systems has shown the appearance of OM generated by electron states near the Dirac-like anticrossing point of the Rashba states.21, 24 However, until now, no similar effect has been detected in 3D TI systems, such as Bi2Se3. Here, by means of magnetic measurements and conduction electron spin resonance (CESR) experiments on Bi-rich Bi2Se3 nanoplatelets, we show for the first time the presence of remarkable surface orbital magnetic properties that couple the spin and orbital degrees of freedom of the 2DEG Rashba states.
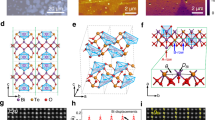
Compared with bulk specimens, nanosized TI materials are compelling systems for probing surface states because of their large surface-to-volume ratio that allows surface states to dominate during bulk measurements. Bi-rich Bi2Se3 nanoplatelets were synthesized in the liquid phase using a simple solvothermal routine, as described in the Materials and methods section. Particle nucleation in the solution occurs by forming charged neutralized layers composed of five covalently bonded atomic sheets, Se1-Bi-Se2-Bi-Se1, defining quintuple layers with a thickness of ∼1 nm5, as shown in Figure 1. These quintuple layers interact weakly through van der Waals (vdW) interactions to form nanocrystals. Atoms adsorbed onto the top surface cannot form covalent bonds with the edge Se atoms, and, consequently, tend to diffuse toward the outer rims. Therefore, the lateral dimensions grow quicker than the vertical dimensions (thickness), and the Bi2Se3 nanoparticles appear as hexagonal platelets, as shown in Figure 1a.
Structural identity of Bi-rich Bi2Se3 nanoplatelets. (a) Transmission electron microscopy (TEM) image of a Bi2Se3 nanoplatelet (scale bar represents 50 nm) of sample BS1; selected area electron diffraction (SAED) from the yellow area (inset) provides proof of the platelet’s single-crystalline nature and reveals that the top (and bottom) facet coincides with the {0 0 0 1} planes of the rhombohedral Bi2Se3. (b) TEM cross-sectional image of a nanoplatelet (scale bar represents 50 nm) of sample BS1. (c) High-resolution TEM (HRTEM) of a cross-sectional spot indicated by a red oval in (b) (scale bar represents 2 nm). The result of the high-resolution analysis and simulation shows that Bi2Se3 and Bi2Se2 coexisting phases are present. (d) X-ray diffraction (XRD) pattern of the Bi2Se3 nanoplatelets (Bi: green spheres; Se: purple spheres) of sample BS1. The results are in agreement with the cross-sectional TEM. (e) 209Bi nuclear magnetic resonance (NMR) spectra of samples BS2 (lower plot) and BS3 (upper plot) at 5 K showing the presence of two non-equivalent Bi sites.
The key factor in the appearance of the unusual OM properties in the Bi2Se3 nanoplatelets is the presence of extra Bi layers intercalated in the vdW gaps, which expand the gaps and modify the Rashba 2DEG states. Ab initio density functional theory calculations have shown that the expansion of the outermost vdW gaps across several quintuplets gives rise to the formation of a number of nested Rashba-type parabolic states,25, 26 which is in agreement with angle-resolved photoemission spectroscopy experimental findings.15 The number and shape of the Rashba states depend on the size and number of expanded vdW gaps. Another important factor for the appearance of OM appears to be intercalation disorder, which is created by random Bi-layer stacking. Whereas OM in clean Rashba systems is formed when EF is near the anticrossing point of the Rashba states, intercalation disorder shifts the relevant energies deep into the conduction band,21, 24 which allows for the appearance of OM in electron-doped TI systems (only energy states at the Fermi level contribute to the OM).
Another significant consequence of the vdW gap expansion is that the TI states are pushed away from the surface to quintuplets deeper within the structure.25, 26 Evidently, the TI states in electron-doped Bi2Se3 are hidden under the 2DEG states. Despite the fact that the TI states are excellently mapped with angle-resolved photoemission spectroscopy, they are very difficult to manipulate. However, spin flips between electrons in the TI states (with clockwise spin helicity) and the outer Rashba sub-band (with counterclockwise spin helicity)15 are not excluded, provided sufficient band overlapping exists. This unveils an exciting perspective, that is, controlling the interband scattering of the Dirac electrons in the TI states by controlling the OM. Therefore, adjusting Bi intercalation is expected to fine-tune the OM and provide a tool for acquiring new experimental insight into the coupling between Rashba and TI states.
Materials and methods
In this work, experimental results from three specimens are presented with an increasing Bi:Se ratio according to the series BS3<BS2<BS1, as determined using detailed transmission electron microscopy energy dispersion spectroscopy analysis (presented in Supplementary Information). Specimen BS1 exhibits the strongest magnetic response and specimen BS3 the weakest. From a series of synthetic efforts, an optimal Bi doping at which the magnetic response is maximum is now understood to exist.
The Bi-rich Bi2Se3 nanoplatelets were synthesized in a liquid phase using a simple solvothermal method. In a typical synthesis procedure, 0.5 mmol of bismuth(III) acetate (Sigma-Aldrich, Taufkirchen, Germany; 99.99%), 0.75 mmol of selenium powder (Sigma-Aldrich; 99.99%) and 1 mmol of triphenylphosphine (Sigma-Aldrich; 99%) were dispersed in 30 ml of oleylamine (Sigma-Aldrich; 70%). The mixture was heated to reflux conditions for 1 h and then allowed to cool to room temperature. The reaction product was isolated via centrifugation, washed thoroughly with high-purity ethanol and allowed to dry in air. A similar method was used by Fei et al.27
Crystallographic characterization was performed on the Bi2Se3 nanoplatelets by powder X-ray diffraction (XRD) using a Siemens D500 (SIMENS AG, Karlsruhe, Germany) diffractometer with Cu Kα radiation (λ=1.5418 Å). Accurate Rietveld analysis of the XRD patterns of the three samples was shown to be unrealistic. An acceptable match was only possible by means of a two-phase analysis of the XRD patterns, consisting primarily of paraguanajuatite and secondarily of nevskite (Figure 1d). The systematic deviation of the theoretical lines from the experimental lines is a strong indication of Bi layers stacked between successive Bi2Se3 quintuplets. A notable difference in the three XRD patterns was observed.
Initial morphological characterization was performed using scanning electron microscopy with an FEI Quanta 250 (FEI, Eindhoven, Holland) coupled with energy dispersion spectroscopy, presented in the Supplementary Information. In-depth structural characterization was performed by transmission electron microscopy using an FEI Tecnai G20 and an FEI CM20 (FEI) (both equipped with energy dispersion spectroscopy) and using a high-resolution transmission electron microscopy (HRTEM) with a Zeiss Ultra Corrected Energy Filtering TEM (LIBRA200MC, Carl Zeiss, Oberkochen, Germany). A cross-section TEM specimen of the Bi2Se3 nanoplatelet was prepared using the focused ion beam method with an FEI Quanta 3D (FEI, Hillsboro, OR, USA). CrystalMaker (CrystalMaker Software Ltd., Oxford, UK) software and MacTempas (Total Resolution LLC, Berkeley, CA, USA) software were used to build the atomic model and simulate the image, respectively.
Additional morphological characterizations were performed using atomic force microscopy with a 3D Multimode Nanoscope operated in a tapping mode using Tap-300G silicon cantilevers (Bruker, Karlsruhe, Germany) with a tip radius of <10 nm and a force constant of ≈20–75 N m−1. Samples were deposited onto silicon wafers (P/Bor, single side polished) using ethanol solutions and drop casting; images are shown in Supplementary Figure S10.
DC magnetization (M) and AC magnetic susceptibility (χ) measurements were performed on a PPMS (Quantum Design, San Diego, CA, USA) magnetometer operating in fields of 0–8 T in the temperature range of 2–300 K. AC susceptibility measurements were performed at three distinct frequencies: 1111, 5111 and 9111 Hz. Isothermal variations of M and χ as a function of the external magnetic field (B=μ0H) were obtained at selected temperatures between 5 and 300 K by sweeping the magnetic field in the range of −6000 to +6000 Gauss in both directions. Zero-field-cooling (ZFC) and field-cooling (FC) measurements were performed as follows: the sample was initially cooled to 5 K under zero applied magnetic field. At 5 K, the sample was subjected to a 100 Oe isothermal magnetization followed by data collection while warming from 5 to 300 K in a magnetic field of 100 Oe (ZFC). Subsequently, a second cycle of measurements was performed while cooling the system from 300 to 5 K and maintaining the applied magnetic field at 100 Oe (FC).
CESR experiments in the temperature range of 5–300 K were performed on a X-band Bruker EPR spectrometer (Bruker, Rheinstetten, Germany) equipped with an Oxford ESR 910 cryostat for low temperature measurements. The microwave frequency was calibrated using a frequency counter, and the magnetic field was calibrated using a NMR Gauss meter.
The 209Bi-pulsed nuclear magnetic resonance (NMR) experiments as a function of temperature were performed at 9.4 T using a homemade broadband NMR spectrometer operating in the frequency range of 5−800 MHz. An Oxford 1200 CF continuous flow cryostat (Oxford Instruments, Oxford, UK) was used for measurements in the temperature range of 3.2−160 K. The spectra were acquired using the frequency point-by-point method with a probe tuned at the Larmor frequency each time. The standard Hahn spin echo (π/2-τ-π-τ-echo) pulse sequence was used with a π/2 pulse width of 9 μs. The interpulse delay time τ was set to a value of 30 μs. The spectra points were acquired by measuring the integrated intensity of the spin echoes with 4096 accumulations for each point and a repetition time of 10 s.
Results and discussion
Cross-sectional HRTEM images (Figures 1b and c and Supplementary Figure S9) provide visual proof that the nanoplatelets presented herein are highly crystalline mosaics of Bi2Se3 and Bi2Se2 phases. The detailed Rietveld analysis of the XRD patterns (Figure 1d) and X-ray energy dispersion spectroscopy (Supplementary Figure S8 and Supplementary Table S1) results are in excellent agreement with the HRTEM results. Specifically, the red solid line is the theoretical XRD pattern from a hypothetical two-phase sample consisting primarily of paraguanajuatite28 (Bi2Se3, a=b=0.418 nm and c=2.84 nm) and secondarily of nevskite29 (Bi2Se2, a=0.42 nm and c=2.22 nm). The experimentally acquired peaks show a systematic deviation from the theoretical values, strongly indicating intermediate range order possibly because of stacking faults. This result is attributed to the presence of Bi layers between the Bi2Se3 quintuplets, giving rise to a compositional variety of (Bi2)m(Bi2Se3)n intercalated nanoplatelets. The presence of two non-equivalent Bi sites corresponding to Bi2Se3 and intercalated Bi, respectively, is further confirmed by observing the two signal components in the 209Bi NMR spectra (Figure 1e) and in the 209Bi NMR spin-lattice relaxation time (T1) measurements (Supplementary Figure S6). Furthermore, T1 vs temperature measurements are shown to follow the Korringa relation (inset in Supplementary Figure S6), which is a direct evidence of metallic behavior, that is, strong electron doping, most probably produced by Se vacancies and BiSe antisite defects.12
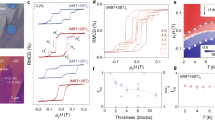
Figure 2 demonstrates the DC magnetization and the AC magnetic susceptibility measurements as a function of the magnetic field for the three specimens. In addition, a schematic presentation of the Rashba spin-split band structure is presented in Figure 2a. An extraordinary and nearly stepwise increase of the magnetization is observed in the field range from −2 to +2 kOe with the signal intensity depending on the degree of Bi intercalation. No hysteresis effects were observed by reversing the direction of the magnetic field. An almost Lorentzian peak at zero magnetic field was observed in the real component of the AC susceptibility (χ'), as seen in Figure 2c. The temperature dependence of χ' with the ZFC and the FC is presented in Figure 2d. Contrary to typical ferromagnetic behavior, samples BS1 and BS2 showed a strong decrease of χ' with cooling, whereas χ' of BS3 was temperature independent. No difference was observed between the ZFC and FC cycles in all three samples, which excludes the possibility of superparamagnetic freezing or other slow relaxing phenomena. This is further confirmed by the fact that the AC susceptibility peak in the χ' vs H curves appears to be independent of the frequency and magnetic field sweep rate, as seen in Supplementary Figures S3–S5. These results are strikingly similar with the recent detection of orbital paramagnetism in the giant Rashba semiconductor BiTeI.21. In that work, in addition to the diamagnetic orbital component that reflected the Berry phase contribution in the OM, an orbital paramagnetic component was also detected.24, 30 Depending on the contribution of the two components, orbital magnetization was observed to decrease or remain invariant with decreasing temperature, which is exactly the case presented herein.
Rashba spin-split two-dimensional electron gas (2DEG) states produce a remarkable stepwise magnetization inversion in the Bi2Se3 nanoplatelets. (a) Schematic presentation of the Rashba spin-split band structure of electron-doped Bi2Se3.15, 16 (b) DC magnetization M vs H measurements of samples BS1 and BS2. No hysteresis effects were observed by reversing the magnetic field. Solid lines are the theoretical simulations based on a toy model Hamiltonian. Inset: spin and orbital motion inversion by reversing the magnetic field according to the model. (c) AC magnetic susceptibility χ′ vs H measurements of sample BS1 at 5 kHz (5–300 K). The solid line is the derivative of the DC magnetization simulation. Inset: real χ′ (red circles) and imaginary χ′′ (green circles) susceptibility peaks at zero magnetic field as a function of temperature. (d) Zero-field-cooling (ZFC) and field-cooling (FC) χ′ vs T at 100 Oe for samples BS1, BS2 and BS3.
The graphical inset in Figure 2b demonstrates what we anticipate to occur when the external magnetic field is inverted. Electrons acquiring a specific trajectory in the E–k space have their spin direction and helicity inverted, which is equivalent to inverting the electron orbital motion in real space. In this context, the DC magnetization and AC susceptibility measurements in the low magnetic field were simulated with a toy model Hamiltonian, which describes electrons moving on a circle of length L enclosing a time-dependent magnetic flux Φ(t)=ϕ+δϕ(t), where ϕ is a constant magnetic flux and δϕ(t)=δϕω cos(ωt) is a small oscillating flux (see Supplementary Information—Part II). For simplicity, electron spins are considered to be oriented in the z-axis, whereas spin-up and spin-down states are associated with clockwise and counterclockwise electron motion, respectively. In this model, the orbital magnetization is analogous to the persistent electron current:

where I0=(eαR)/(ℏL) and T*=(aR)/(πkBL). A very interesting similarity between the experimental data and the theoretical simulation is observed (Figure 2b). According to this model, spin-up and spin-down eigenstates are doubly degenerate in zero magnetic field, that is, the magnetic flux ϕ=0 (Supplementary Figure S11). Upon an infinitesimal increase in the flux, the spin-down state (left-handed spin texture in Bi2Se3) becomes occupied and the spin-up state (right-handed) becomes empty. The reverse occurs upon an infinitesimal decrease in the flux. Therefore, increasing the flux infinitesimally from (ϕ/ϕ0)=0 has a net effect of replacing the spin-up state by a spin-down state, thereby yielding a positive jump of 2I0 in the current. Experimentally, this is observed as a strong paramagnetic jump in the M vs H curves with a spin component and an orbital component. By increasing the field, the diamagnetic part, that is, the Berry phase, contribution to the orbital component increases,30 giving rise to a linear decrease in the orbital magnetization (Figure 2b). Remarkably, sample BS1 exhibits a weak orbital diamagnetic component, as implied by the small negative baseline in the magnetic susceptibility curves in Figure 2c, and the orbital magnetization appears to saturate (the net spin magnetization of the Rashba states is zero).
The viewpoint outlined above is in contrast with recent results observed in Bi2Se3 single crystals by Zhao et al.,31 in which a temperature-independent χ′ vs H singularity was assigned to spin flips between Zeeman-split TI states. Such behavior is not expected in electron-doped Bi2Se3, in which surface magnetism resides on the electron states at the Fermi level, that is, deep in the conduction band.
To acquire information with respect to the temperature evolution of this intriguing OM, CESR experiments were conducted on all three samples. Comparative room temperature spectra are presented in Figure 3c. The results are in excellent agreement with the AC susceptibility measurements, which affirms the assignment of the signals to conduction electrons and not ferromagnetic or paramagnetic impurities (see also Supplementary Figures S1 and S2). In a typical CESR experiment, the application of a magnetic field produces electron band spin splitting, whereas the microwave irradiation induces inversion of the electron spin population in the spin-split conduction band at the Fermi level. Therefore, the CESR signal intensity is expected to be proportional to the electron density of the states at the Fermi level, ICESR≈ns(EF)g. However, in the presence of Rashba interaction, as in our Bi-doped Bi2Se3, the Bychkov–Rashba-type SOC should be taken into consideration.32 This is equivalent to an effective magnetic field: the so-called Rashba field with magnitude  ,33 which follows a planar spiral, as shown schematically in Figure 3a. Evidently, in the presence of
,33 which follows a planar spiral, as shown schematically in Figure 3a. Evidently, in the presence of  , CESR is determined by the effective resonance field
, CESR is determined by the effective resonance field  (Figure 3b). We note that for in situ cleaved single crystalline Bi2Se3, αR was found to be equal to 0.79 eVÅ, corresponding to ESR signals in the THz frequencies.16 Therefore, observing the CESR signal in the X band is highly surprising and indicates that either αR in the nanoplatelets is orders of magnitude smaller compared with that in single crystalline Bi2Se3 or that the CESR signals are produced by electrons in shallow sub-bands of the 2DEG states near the surface with significantly weaker Rashba splitting.15 This is in agreement with the prediction that vdW expansion weakens the Rashba splitting.25, 26
(Figure 3b). We note that for in situ cleaved single crystalline Bi2Se3, αR was found to be equal to 0.79 eVÅ, corresponding to ESR signals in the THz frequencies.16 Therefore, observing the CESR signal in the X band is highly surprising and indicates that either αR in the nanoplatelets is orders of magnitude smaller compared with that in single crystalline Bi2Se3 or that the CESR signals are produced by electrons in shallow sub-bands of the 2DEG states near the surface with significantly weaker Rashba splitting.15 This is in agreement with the prediction that vdW expansion weakens the Rashba splitting.25, 26
Two-dimensional electron gas (2DEG) states and growing Rashba field with gradual cooling. (a) In k-space, the Rashba field  circulates in the kx, ky plane with magnitude
circulates in the kx, ky plane with magnitude  . (b) In real space during the conduction electron spin resonance (CESR) experiments, electrons of a 2DEG in the presence of a Rashba field precess with Larmor frequency
. (b) In real space during the conduction electron spin resonance (CESR) experiments, electrons of a 2DEG in the presence of a Rashba field precess with Larmor frequency  . (c) CESR signals of samples BS1, BS2 and BS3. The signal intensity correlates excellently with the signal intensity of the AC magnetic susceptibility. (d) CESR signals of sample BS2 at various temperatures. The signal shift to a lower magnetic field indicates an increase in
. (c) CESR signals of samples BS1, BS2 and BS3. The signal intensity correlates excellently with the signal intensity of the AC magnetic susceptibility. (d) CESR signals of sample BS2 at various temperatures. The signal shift to a lower magnetic field indicates an increase in  because of cooling.
because of cooling.
The CESR spectra of sample BS1 as a function of temperature are presented in Figure 4; the signals were remarkably stronger compared with BS2 (shown in Figure 3d), which is in agreement with the magnetic measurements. At room temperature, the spectrum exhibited a broad line with isotropic g≈2.174, which corresponds to the Rashba field BR≈270 G. By lowering the temperature, the integrated signal intensity decreases rapidly, whereas the signal shifts to lower magnetic fields, indicating a strong increase in BR and, consequently, aR. Furthermore, the peak-to-peak linewidth increases, which is consistent with an Eliot-type spin-phonon relaxation mechanism,34 ΔB∝1/T1∝(Δg)2τ−1, where Δg=(g−2.0023), and τ−1 is the conduction electron scattering rate.
Conduction electron spin resonance (CESR) signals of sample BS1 in the temperature range of 5–295 K. The upper inset shows the shift in the resonance magnetic field compared with the resonance field of a free electron system. The lower inset demonstrates the variation of the line width (yellow circles) and the signal intensity (green circles) with temperature.
The temperature dependence of aR is an effect observed in several semiconductor heterostructures.35 In all these systems, by neglecting the band structure effect on the SOC, αR may be expressed as αR=g(g−1)(πeℏ2ɛ)/(4m*2c2), where ɛ is the induced electric field and m* is the effective electron mass. In this approximation, the temperature dependence of αR may be explained by the temperature dependence of g and m*, which are both dependent on the dilatational and phononic variation of the conduction band.36 We anticipate that a relevant mechanism may be the origin of the observed temperature dependence of αR in the Bi2Se3 nanoplatelets. Another possibility is that the vdW gaps shrink with decreasing temperature, thus giving rise to a substantial increase in αR.
Conclusions
We have shown that sweeping a weak magnetic field from negative to positive values induces a stepwise reversal in the magnetization of bismuth-rich Bi2Se3 nanoplatelets, which is attributed to spin flips between Rashba states with opposite spin helicity. The intensity of this unusual OM depends strongly on the degree of Bi intercalation, which controls the vdW gap expansion and, thus, provides a unique way for spin engineering. Random stacking of the Bi layers appears to have an important role in the appearance of this novel effect. According to theoretical predictions, randomness shifts the density of electron states with nonzero OM deep into the conduction band.24 Another challenging issue is whether OM provides a way to control interband electron spin scattering between the TI and Rashba states, that is, to control the conductivity of the Dirac electrons in the TI states. This is very important in electron-doped 3D TI systems, as the Dirac states in these systems are well hidden under the 2DEG surface electron states. Evidently, the discovery of this unique OM has opened new perspectives for novel applications ranging from magnetic spin control and quantum computing to plasmonics and catalytic chemistry.37, 38
References
Hsieh, D., Xia, Y., Qian, D., Wray, L., Meier, F., Dil, J. H., Osterwalder, J., Patthey, L., Fedorov, A. V., Lin, H., Bansil, A., Grauer, D., Hor, Y. S., Cava, R. J. & Hasan, M. Z. Observation of Time-reversal-protected single-Dirac-cone topological-insulator states in Bi2Te3 and Sb2Te3 . Phys. Rev. Lett. 103, 146401 (2009).
Xia, Y., Qian, D., Hsieh, D., Wray, L., Pal, A., Lin, H., Bansil, A., Grauer, D., Hor, Y. S., Cava, R. J. & Hasan, M. Z. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009).
Hasan, M. Z. & Kane, C. L. Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Hsieh, D., Qian, D., Wray, L., Xia, Y., Hor, Y. S., Cava, R. J. & Hasan, M. Z. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–974 (2008).
Zhang, H., Liu, C.-X., Qi, X.-L., Dai, X., Fang, Z. & Zhang, S.-C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5 (6), 438–442 (2009).
Pesin, D. & MacDonald, A. H. Spintronics and pseudospintronics in graphene and topological insulators. Nat. Mater. 11, 409–416 (2012).
Mellnik, A. R., Lee, J. S., Richardella, A., Grab, J. L., Mintun, P. J., Fischer, M. H., Vaezi, A., Manchon, A., Kim, E. A., Samarth, N. & Ralph, D. C. Spin-transfer torque generated by a topological insulator. Nature 511, 449–451 (2014).
Das, S. S., Freedman, M. & Nayak, C. Topological quantum computation. Phys. Today 59, 32–38 (2006).
Chen, Y. P. Topological insulator-based energy efficient devices in Micro- and Nanotechnology Sensors, Systems, and Applications IV (eds George T., Islam M. S. & Dutta A.) (USA Society of Photo-Optical Instrumentation Engineers, Baltimore, MD, USA, 2012).
Baker, A. A., Figueroa, A. I., Collins-McIntyre, L. J., van der Laan, G. & Hesjedal, T. Spin pumping in ferromagnet-topological insulator-ferromagnet heterostructures. Sci. Rep. 5, 7907 (2015).
Galanakis, D. & Stanescu, T. D. Electrostatic effects and band bending in doped topological insulators. Phys. Rev. B. 86, 195311 (2012).
Huang, F. T., Chu, M. W., Kung, H. H., Lee, W. L., Sankar, R., Liou, S. C., Wu, K. K., Kuo, Y. K. & Chou, F. C. Nonstoichiometric doping and Bi antisite defect in single crystal Bi2Se3 . Phys. Rev. B. 86, 081104 (2012).
Kong, D., Cha, J. J., Lai, K., Peng, H., Analytis, J. G., Meister, S., Chen, Y., Zhang, H. J., Fisher, I. R., Shen, Z. X. & Cui, Y. Rapid surface oxidation as a source of surface degradation factor for Bi2Se3 . ACS Nano. 5, 4698–4703 (2011).
Bianchi, M., Guan, D., Bao, S., Mi, J., Iversen, B. B., King, P. D. C. & Hofmann, P. Coexistence of the topological state and a two-dimensional electron gas on the surface of Bi2Se3 . Nat. Commun. 1, 128 (2010).
King, P. D. C., Hatch, R. C., Bianchi, M., Ovsyannikov, R., Lupulescu, C., Landolt, G., Slomski, B., Dil, J. H., Guan, D., Mi, J. L., Rienks, E. D., Fink, J., Lindblad, A., Svensson, S., Bao, S., Balakrishnan, G., Iversen, B. B., Osterwalder, J., Eberhardt, W., Baumberger, F. & Hofmann, P. Large tunable Rashba spin splitting of a two-dimensional electron gas in Bi2Se3 . Phys. Rev. Lett. 107, 096802 (2011).
Zhu, Z. H., Levy, G., Ludbrook, B., Veenstra, C. N., Rosen, J. A., Comin, R., Wong, D., Dosanjh, P., Ubaldini, A., Syers, P., Butch, N. P., Paglione, J., Elfimov, I. S. & Damascelli, A. Rashba spin-splitting control at the surface of the topological insulator Bi2Se3 . Phys. Rev. Lett. 107 (18), 186405 (2011).
LaShell, S., McDougall, B. A. & Jensen, E. Spin splitting of an Au(111) surface state band observed with angle resolved photoelectron spectroscopy. Phys. Rev. Lett. 77 (16), 3419–3422 (1996).
Hoesch, M., Muntwiler, M., Petrov, V. N., Hengsberger, M., Patthey, L., Shi, M., Falub, M., Greber, T. & Osterwalder, J. Spin structure of the Shockley surface state on Au(111). Phys. Rev. B. 69, 241401 (2004).
Ishida, H. Rashba spin splitting of Shockley surface states on semi-infinite crystals. Phys. Rev. B. 90, 235422 (2014).
Hernando, A., Crespo, P. & García, M. A. Origin of orbital ferromagnetism and giant magnetic anisotropy at the nanoscale. Phys. Rev. Lett. 96, 057206 (2006).
Schober, G. A. H., Murakawa, H., Bahramy, M. S., Arita, R., Kaneko, Y., Tokura, Y. & Nagaosa, N. Mechanisms of enhanced orbital dia- and paramagnetism: application to the Rashba semiconductor BiTeI. Phys. Rev. Lett. 108, 247208 (2012).
Meyer, A. J. P. & Asch, G. Experimental g′ and g values of Fe, Co, Ni, and their alloys. J. Appl. Phys. 32, S330–S333 (1961).
Koshino, M. & Ando, T. Anomalous orbital magnetism in Dirac-electron systems: Role of pseudospin paramagnetism. Phys. Rev. B. 81, 195431 (2010).
Zhu, G., Yang, S. A., Fang, C., Liu, W. M. & Yao, Y. Theory of orbital magnetization in disordered systems. Phys. Rev. B. 86, 214415 (2012).
Eremeev, S. V., Vergniory, M. G., Menshchikova, T. V., Shaposhnikov, A. A. & Chulkov, E. V. The effect of van der Waal's gap expansions on the surface electronic structure of layered topological insulators. N. J. Phys. 14, 113030 (2012).
Vergniory, M. G., Menshchikova, T. V., Eremeev, S. V. & Chulkov, E. V. Ab initio study of 2DEG at the surface of topological insulator Bi2Te3. JETP Lett. 95 (4), 213–218 (2012).
Fei, F., Wei, Z., Wang, Q., Lu, P., Wang, S., Qin, Y., Pan, D., Zhao, B., Wang, X., Sun, J., Wang, X., Wang, P., Wan, J., Zhou, J., Han, M., Song, F., Wang, B. & Wang, G. Solvothermal synthesis of lateral heterojunction Sb2Te3/Bi2Te3 nanoplates. Nano Lett. 15, 5905–5911 (2015).
Nakajima, S. The crystal structure of Bi2Te3−xSex . J. Phys. Chem. Solids 24, 479–485 (1963).
Stasova, M. M. Crystal structure of bismuth selenides and bismuth and antimony tellurides. J Struct. Chem. 8, 584–589 (1967).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Zhao, L., Deng, H., Korzhovska, I., Chen, Z., Konczykowski, M., Hruban, A., Oganesyan, V. & Krusin-Elbaum, L. Singular robust room-temperature spin response from topological Dirac fermions. Nat. Mater. 13, 580–585 (2014).
Litvinov, V. I. Spin current and electrical polarization in GaN double-barrier structures. Phys. Rev. B. 76, 245305 (2007).
Meier, L., Salis, G., Shorubalko, I., Gini, E., Schon, S. & Ensslin, K. Measurement of Rashba and Dresselhaus spin-orbit magnetic fields. Nat. Phys. 3, 650–654 (2007).
Feher, G. & Kip, A. F. Electron spin resonance absorption in metals. I. Experimental. Phys. Rev. 98, 337–348 (1955).
Bandyopadhyay, S. & Cahay, M. Introduction to Spintronics, CRC Press: Boca Raton, FL, USA, (2008).
Zhang, L., Chen, Y. B., Zhang, B., Zhou, J., Zhang, S., Gu, Z., Yao, S. & Chen, Y. F. Sensitively temperature-dependent spin–orbit coupling in SrIrO3 thin films. J. Phys. Soc. Jpn. 83, 054707 (2014).
Chen, H., Zhu, W., Xiao, D. & Zhang, Z. C. O. CO oxidation facilitated by robust surface states on Au-covered topological insulators. Phys. Rev. Lett. 107, 056804 (2011).
Kong, D. & Cui, Y. Opportunities in chemistry and materials science for topological insulators and their nanostructures. Nat. Chem. 3, 845–849 (2011).
Acknowledgements
This work has been partially supported by the European FP7-2011-IRSES project ‘Nanomag’ with grant agreement no. 295190. We wish to extend our gratitude to Stavros M Katsiotis from the National Technical University of Athens for preparing the schematics used in Figures 2 and 3. HJK, JGK, SGL, YMK, SJY and JHL are grateful for the financial support from the Korea Basic Science Institute (T35210).
Author contributions
HJK, MSK, SA and GP conceived and designed the experiments, performed the theoretical analysis and wrote the majority of the paper (with contribution from all coauthors). IZ, VT, MSK, AK and DG synthesized and characterized the samples (XRD, scanning electron microscopy and initial TEM). NB, JGK and SGL carried out the HRTEM and structural analysis experiments. YMK and SJY carried out the HRTEM image simulation and modeling. JHL prepared and measured the focused ion beam specimens. MP and MK performed the magnetic measurements. GM and YS performed the CESR measurement. NP, MF, and GP carried out the NMR experiments.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies the paper on the NPG Asia Materials website
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kim, H., Katsiotis, M., Alhassan, S. et al. Unexpected orbital magnetism in Bi-rich Bi2Se3 nanoplatelets. NPG Asia Mater 8, e271 (2016). https://doi.org/10.1038/am.2016.56
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/am.2016.56