Abstract
The topological spin textures in magnetic vortices in confined magnetic elements offer a platform for understanding the fundamental physics of nanoscale spin behavior and the potential of harnessing their unique spin structures for advanced magnetic technologies. For magnetic vortices to be practical, an effective reconfigurability of the two topologies of magnetic vortices, that is, the circularity and the polarity, is an essential prerequisite. The reconfiguration issue is highly relevant to the question of whether both circularity and polarity are reliably and efficiently controllable. In this work, we report the first direct observation of simultaneous control of both circularity and polarity by the sole application of an in-plane magnetic field to arrays of asymmetrically shaped permalloy disks. Our investigation demonstrates that a high degree of reliability for control of both topologies can be achieved by tailoring the geometry of the disk arrays. We also propose a new approach to control the vortex structures by manipulating the effect of the stray field on the dynamics of vortex creation. The current study is expected to facilitate complete and effective reconfiguration of magnetic vortex structures, thereby enhancing the prospects for technological applications of magnetic vortices.
Similar content being viewed by others
Introduction
A magnetic vortex in a micron-sized ferromagnetic element consists of the central core (polarity, p) in which the magnetization is pointing into the out-of-plane direction either up (p=+1) or down (p=−1), and the in-plane magnetization (circularity, c) rotates around the central core in either the clockwise (c=+1, CW) or counter-clockwise (c=−1, CCW) direction.1, 2 Because both circularity and polarity can be specified by two independent values, that is, c=±1 and p=±1, four distinct spin states can exist in a single magnetic element with the combination of circularity and polarity. Magnetic vortices have been intensively studied due to their compelling physical behavior3, 4, 5, 6, 7 and their potential in a wide range of applications such as data storage,8, 9 signal transfer,10, 11, 12 logic devices,13 transistors14 and artificial skyrmion crystals.15, 16, 17, 18 With respect to practical application of magnetic vortices in advanced nanotechnologies, one of the critical factors is the effective reconfigurability of two topologies, c and p, particularly within large and densely packed arrays of magnetic elements.19, 20 As a representative example, for successful achievement of vortex-based signal transfer and logic and transistor operations, the desired configurations of magnetic vortex states must be first established.10, 11, 12, 13, 14 Additionally, uniformly arranged vortex structures are also required to generate artificial skyrmion crystals based on magnetic vortices in proximity to perpendicularly magnetized thin films.15, 16, 17, 18
For effective reconfiguration of magnetic vortex structures, one key issue is reliable and efficient control of both c and p in magnetic vortices, which is also vital for storage applications. Thus far, both static and dynamic studies on the control of vortex structures have been primarily dedicated to manipulation of either the c or p alone.8, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 A few attempts have been made to control both c and p, but these attempts have been conducted without repetition, meaning that only a single event of control has been investigated.32, 33 Therefore, reliability and repeatability for control of both topological features has not yet been addressed. In addition, multiple manipulation methods, for example, both in-plane and out-of-plane magnetic fields, have been applied to achieve control of both c and p. Reliable and technically plausible control of both c and p with the application of a single control factor, such as either an in-plane or out-of-plane field, and an in-depth understanding of relevant physics remain as challenges.
In the current investigation, we demonstrate that application of an in-plane magnetic field alone enables simultaneous control of c and p in an array of asymmetric permalloy (Py, Ni80Fe20) disks with one flat-edge side. The reliability in the control of vortex structures is found to be sensitive to the geometry of the nanodisk arrays, including the flat-edge ratio (r, as defined in Figure 1) and the disk height (h). Based on a comprehensive understanding of the stray field effect on the dynamic process of vortex creation, we propose a new means of vortex-state control that enables the global and/or local reconfiguration of vortex structures in closely packed permalloy disks.
Magnetic imaging of asymmetrically shaped disks. Schematic diagram of asymmetric disks with radius R=500 nm, height h=100 nm and edge ratio r=0.2R within an array with an interdisk distance of d=200 nm. Insets show representations of MTXM images of the in-plane magnetic components observed in a positive field sequence from +100 to 0 mT.
Materials and methods
Sample preparation
Py disk arrays were fabricated on X-ray transparent silicon-nitride membranes using e-beam lithography and sequential lift-off processes. The disk radius (R) and interdisk distance (d) were fixed at R=500 nm and d=200 nm, and the disk height (h) and flat-edge ratio (r) were varied from h=40 to 100 nm and from r=0.1R to 0.2R.
Imaging of magnetic vortex structures
To observe the complete vortex structures (i.e., both circularity and polarity), we used magnetic full-field transmission soft X-ray microscopy (MTXM) at the Advanced Light Source (XM-1, beamline 6.1.2.).34 In-plane and out-of-plane magnetizations were respectively imaged by mounting the specimens at 60° and 90° angles with respect to the incident X-ray beam direction. The magnetic contrast at XM-1 is created by an X-ray magnetic circular dichroism mechanism. The X-ray beam energy was set at the Fe L3 edge (707 eV) of the X-ray absorption spectra. To enhance the magnetic contrast and eliminate any non-magnetic background, the images collected in the remanent state were normalized by a reference image recorded at the saturation state. To saturate the Py disks, an in-plane magnetic field of +100 or −100 mT was applied parallel to the flat edge of disks, as shown in Figure 1.
Micromagnetic simulations
Micromagnetic simulations were conducted with disks of 2R=999 nm, h=40 nm, r=99 nm (~0.2R) and an interdisk distance of d=201 nm, the dimensions of which are nearly identical to those of the disks (2R=1000 nm, h=40 nm, r=100 nm (~0.2R) and d=200 nm) studied in the experiments. The lateral dimensions of the disks and the interdisk distance were multiples of 3 nm due to the cell size of 3 × 3 × 5 nm3 chosen for the simulations. The micromagnetic simulations were performed using the object-oriented micromagnetic framework (OOMMF) code,35 which numerically solves the Landau–Lifshitz–Gilbert equation36, 37 for the local magnetization vector  with phenomenological damping constant α, gyromagnetic ratio γ and effective field Heff. The standard material parameters for Py were used: saturation magnetization Ms=800 kA m−1; exchange stiffness Aex=13 pJ m−1; damping constant α=0.01; and zero magnetocrystalline anisotropy. Periodic boundary conditions were used in the simulations to take account of stray fields induced by adjacent disks within the arrays of disks.
with phenomenological damping constant α, gyromagnetic ratio γ and effective field Heff. The standard material parameters for Py were used: saturation magnetization Ms=800 kA m−1; exchange stiffness Aex=13 pJ m−1; damping constant α=0.01; and zero magnetocrystalline anisotropy. Periodic boundary conditions were used in the simulations to take account of stray fields induced by adjacent disks within the arrays of disks.
Results and discussion
Direct observation of magnetic vortex structures
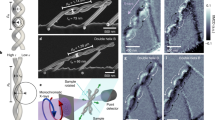
Figure 1 shows the schematic diagram of a Py disk array with a radius of R=500 nm, a height of h=100 nm, an interdisk distance of d=200 nm and a flat-edge ratio of r=0.2R. The creation of vortex structures in the disk array was achieved using a positive field sequence: a magnetic field of +100 mT is applied in the positive x direction (H=+Hx) parallel to the flat edges of disk elements to fully saturate the disks and is subsequently relaxed to the remanent state at 0 mT by turning off the magnetic field. The inset in Figure 1 illustrates MTXM images of the in-plane spin configurations observed in the array after the positive field sequence. The direction of magnetization in the disk plane is indicated with a white arrow. The in-plane magnetic contrast allows the value of c to be determined. It is clearly evident that with the positive field sequence, the preferably created circularity is CCW(c=−1). To determine whether any field-direction effect exists on the type of created circularity, we also observed the vortex structures formed after the following sequence: a field of −100 mT is applied in the negative x direction (H=−Hx) and is subsequently turned off to 0 mT (hereafter referred to as the negative field sequence). In Figure 2a, we show a representative series of images for the in-plane domain structures taken from two different field sequences in the disk arrays with edge ratios r=0.1R and r=0.2R. In both arrays, the CW (c=+1) circularity is created by the negative field sequence, and the CCW (c=−1) circularity is created by the positive field sequence. This result shows that circularity can be selectively created in the asymmetric disks by altering the direction of the in-plane field. It should be noted that the rotational sense of circularity selected by each field sequence in the disks within the array shown in Figure 2a is opposite to the one formed in an isolated disk with the identical field sequence.24, 26, 27 Under the positive (negative) field sequence, CCW (CW) circularity is generated in the disks within the array, whereas CW (CCW) circularity is created in an isolated disk.24, 26, 27 To understand the change in the type of created circularity between disks within the array and a single isolated disk, we considered the effect of the stray field on the vortex creation process. Based on micromagnetic simulations for vortex formation with and without consideration of the stray field, we confirmed that the dynamics of vortex creation could be significantly altered by the stray field. Under the influence of the stray field, the dynamic process of vortex formation in the positive (negative) field sequence proceeds toward creation of the CCW (CW) circularity, as observed in disks within the array (Figure 2a). The detailed dynamic procedure and the stray field effect on the dynamics are discussed later.
Controllability of circularity in asymmetric disk arrays with different geometries. (a) MTXM images of in-plane domain structures taken from four successive measurements by alternating positive and negative field sequences in the disk arrays with R=500 nm, h=100 nm and d=200 nm. (b) Controllability of circularity by altering the direction of the applied field investigated in disk arrays (R=500 nm, d=200 nm) with different edge ratios and disk heights. The values are obtained from statistical analysis of generation probabilities of c in 1000 vortex formation events for each array. The error bar represents the standard deviation of controllability in 25 individual disks.
Controllability of circularity in asymmetric disk arrays
The reliability of circularity control (controllability) was quantitatively investigated by switching the direction of the external field for various arrays of disks with different disk heights and flat–edge ratios, as shown in Figure 2b. To accumulate statistically meaningful data, the experimental procedure schematized in Figure 2a was repeated 40 times, and vortex structures in 25 individual disks were examined in each array. The generation rate of an identical circularity in any given disk within 40 repetitions was counted as the metric for controllability, where the controllability is defined as 100% (0%) if the generation rate of CCW circularity is 100% (50%) within 40 repeated cycles with the positive field sequence (for which CCW circularity is predominantly generated). In Figure 2b, the error bar represents the standard deviation of controllability over the 25 disks. The reliability for formation of a vortex structure with the same circularity in asymmetric disks is certainly improved compared with the case of symmetric circular disks. The reliability of circularity control is greater than 95% in asymmetric disks with h=100 nm, as shown in Figure 2b, whereas the probability for formation of vortex structures with the same circularity determined from statistical measurements (20 repetitions, 25 individual disks) is less than 35% in the case of symmetric full disks with the same height of 100 nm. In Figure 2b, we find that the controllability is sensitive to the geometry of the disk arrays. As the flat–edge ratio increases from r=0.1R to 0.2R, the controllability increases, and disks of h=100 nm show higher controllability than those of h=40 or 70 nm. The high controllability of greater than 90% observed in the 100-nm-thick disks, regardless of the edge ratio, might be due to the less pronounced impact of thermal fluctuations associated with the large volume of disks. Indeed, thermal fluctuation38 is an inherent factor that hinders reliable control of magnetic processes.39, 40 The intensity of thermal fluctuation occurs in inverse proportion to an activation volume, which is related to the thermal effect.41 In vortex formation, the disk volume could be considered as an activation volume42 because the formation process undergoes multiple steps of nucleation and annihilation of the vortex and anti-vortex occurring in the vortex core and also over the entire disk volume.43 The effective thermal effect is reduced by a factor of 2.5 as the disk height increases from 40 to 100 nm, that is, disks of h=100 nm are less prone to thermal fluctuations than the thinner disks. Consequently, in larger-volume disks, the same type of vortex structure can be more reliably created.
Simultaneous control of circularity and polarity in asymmetric disks
For disks of h=100 nm and r=0.2R, which exhibit approximately 97% accuracy in circularity control, we verified the simultaneous control of c and p through direct imaging of circularity and polarity. Figure 3a shows MTXM images of in-plane and out-of-plane magnetic structures observed in an identical region of the array. In the out-of-plane MTXM images, the white and black spots in the centers of the disks indicate down and up polarities, respectively. Remarkably, the change of field direction triggers switching of the circularity and the polarity. CW circularity (c=+1) with a down polarity (p=−1) is formed after the positive field sequence, whereas CCW circularity (c=−1) with an up polarity (p=+1) is most often generated after the negative field sequence. A simplified illustration of this observed phenomenon is shown in Figure 3b. The results indicate that simultaneous control of c and p is feasible using a single manipulation process, that is, application of an in-plane magnetic field in the asymmetric disks. This result suggests the possibility of highly efficient reconfiguration of the magnetic-vortex structures in nanodisk arrays. Our result is unexpected and intriguing because only c has been considered controllable in asymmetric disks.24, 25, 26, 27, 28 Simultaneous control of c and p is thought to be related to the asymmetric nature in the formation process of vortex states, as reported in our previous work.7 It was found that two different vortex state groups with cp=+1 and cp=−1 are not energetically equivalent in a single circular disk due to both intrinsic and extrinsic factors. Either cp=+1 or cp=−1 is more stable than the other, and the energetically favored vortex group predominantly forms. In the case of asymmetric disks (Figure 3a), cp=−1 is more favored than cp=+1. If c=+1 switches to c=−1, p tends to flip from p=−1 to p=+1 to form cp=−1. Notably, c and p are not independent, but they are linked with each other in that c and p tend to switch together. This intrinsic connection between c and p could be a critical feature that must be seriously considered for individual control of c and p. In contrast to circular disks, circularity in asymmetric disks is controllable by altering the direction of the magnetic field, which allows for simultaneous control of c and p in such disks. The reliability of simultaneous control of c and p, as determined by a statistical ensemble of 300 events (15 repetitions, 20 individual disks), was found to be 77±17 and 79±16% in disks of 100 nm thickness with 0.2R and 0.1R edge ratios, respectively. The errors correspond to the s.d. of reliability for the 20 disks. It should be noted that the data obtained from the statistical ensemble cover any possible randomness or imperfection of vortex control that can exist in certain of the disks, as shown in one of the six disks in the lower-middle panel and two of the six disks in the lower-right panel, as indicated by white dots in Figure 3a. The reliability of vortex control can differ from one disk to another, mostly due to randomly generated surface-related extrinsic factors such as roughness and defects. It is expected that the accuracy of controlling both c and p can be further enhanced by optimizing the geometries of asymmetric disk arrays.
Simultaneous control of circularity and polarity in asymmetric disks. (a) MTXM images of in-plane and out-of-plane magnetic structures observed in an identical region of the disk array (R=500 nm, h=100 nm and r=0.2R). (b) Simplified illustration of control of complete vortex structure, that is, both c and p, by changing the direction of the in-plane field.
New approach for control of vortex structures in asymmetric disks
Finally, we propose a new approach to controlling c in asymmetrically shaped disks. As demonstrated in Figure 3, because simultaneous control of c and p is feasible when c is reliably controlled, this method could replace that involving alteration of the direction of an in-plane field for control of both c and p in asymmetric disks. As noted in Figure 2, the stray field is the critical magnetic factor for determination of finally formed c states in asymmetric disks because it significantly affects the dynamics in the early stage of the vortex formation process.43 A certain type of circularity, ether c=+1 or c=−1, is selected according to whether the stray field exists or not. Our approach to the control of c is to manipulate the stray field effect on the dynamic process of vortex creation using an additional, static and uniform field (hereafter, the control field). The control field can create an effective stray field environment of closely packed disks that resembles one of an isolated disk and vice versa.
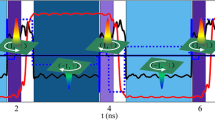
First, to fully understand the influence of the stray field on the process of vortex structure formation, micromagnetic simulations of the dynamics of vortex formation in an isolated element and the same element with neighboring identical elements have been performed without considering the control field. The two disks were set to the same geometry of 2R=999 nm, h=40 nm, r=99 nm (~0.2R) and an interdisk distance of d=201 nm, parameters that are nearly equal to those (2R=1000 nm, h=40 nm, r=100 nm (~0.2R) and d=200 nm) of the disk studied in the experiments. Figure 4a shows images of the simulated dynamic processes in an isolated single disk (upper) and in a disk within the array of d=201 nm (lower). The color on the disk surface represents the curl of in-plane magnetization (m). The red (blue) color indicates the CCW (CW) winding direction of m, and the arrow indicates the direction of in-plane magnetization on the disk surface. To trigger vortex creation, the disks were initially saturated at +100 mT and subsequently relaxed to 0 mT within τ=4.4 ns. The strength of the stray field generated in the disk array of d=201 nm during the process was estimated to be approximately 10 mT in the +x direction. In the early stage of vortex formation (⩽7.2 ns for isolated disks (upper), ⩽9.7 ns for a disk within an array (lower)), nearly identical dynamic processes were observed in the two disks. Two vortices are injected from the left and right sides of the disk, respectively, and they move closer to each other. Because these disks have the same CCW circularity (red), a cusp-shaped magnetization configuration is formed between them and is transformed into an oxbow-shaped configuration (t=11.6 ns (upper) and 12. 3 ns (lower)). As the dynamics progress, an additional CW vortex appears (t=12.1 ns (upper) and 15.4 ns (lower)). The effect of the stray field becomes obvious from comparison of the isolated disk at t=14 ns (upper) with the disk within the array at 15.8 ns (lower). In the isolated disk, the initially injected CCW vortices move toward the flat edge of the disk, and the newly created CW vortex (blue) is located in the central region. However, due to the stray field in the disk within the array of d=201 nm, the two CCW vortices remain at the center, and the CW vortex is annihilated at the round edge. Consequently, in the isolated disk, the inner-disk CW vortex becomes the final vortex structure, whereas in the disk within the array, one of the initially injected CCW vortices survives as the ultimate vortex. In summary, the stray field in the d=201 nm (~10 mT) array stimulates the creation of CCW circularity in the positive field sequence from +100 to 0 mT.
Control of vortex structures by manipulation of the stray field effect on the dynamic process of vortex creation. (a) Series of snapshot images taken from simulations of vortex formation in an isolated disk (upper) and in a disk within a d=201 nm array (lower). The disks have dimensions of 2R=999 nm radius, h=40 nm height and r=99 nm flat–edge ratio (~0.2R). In this work, the disks were immediately relaxed to 0 mT from a 100 mT saturation state without application of a control field. (b) Dynamic process observed by simulations with control fields of +10 mT and −10 mT additionally applied during the relaxation process of an isolated disk (upper) and a disk within the array (lower), respectively. The color on the disk surface corresponds to the curl of in-plane magnetization. The blue and red colors indicate the CW and CCW circularities, respectively.
To clarify our concept of circularity control using a control field, we again conducted micromagnetic simulations in identical systems. The disks were relaxed to 0 mT from the fully saturated state at +100 mT, according to the procedure outlined in Figure 4a. However, in this simulation, control fields of ±10 mT were additionally applied at the moment when the 100 mT saturation field was turned off. By turning on the control field of +10 mT (−10 mT) in the positive field sequence, the saturation field of +100 mT is reduced directly to +10 mT (−10 mT). The purpose of the control field is to create an environment similar to that in which the stray field exists in an isolated disk and to create the condition under which no stray field exists in the disk within the array by countering the influence of the stray field induced by adjacent disks within the array. The control-field strength (10 mT) was chosen based on the results shown in Figure 4a, in which case the stray field strength in the disk array of d=201 nm was approximately 10 mT. The direction of the control field was set as +x for the isolated disk and −x for the disk within the array, considering the fact that the stray field in the array of d=201 nm occurred in the +x direction (Figure 4a). Snapshot images taken from the simulations are displayed in Figure 4b. The dynamics in the isolated disk with the applied +10 mT control field (upper) are analogous to those observed in the disk within the array (Figure 4a). The initially injected CCW vortices (red) shift to the center of the disk during the annihilation of the CW vortex (blue) at the 16.4 ns stage, and consequently, the final vortex is CCW, as in the case of the disk within the d=201 nm array with no control field (Figure 4a). At the same time, the dynamic process in the disk within the array with the induced −10 mT control field (lower) was almost identical to that observed in the isolated disk (Figure 4a). The CW vortex newly created at the 12.2 ns stage is located in the middle of the disk with the two CCW circularities pushed toward the edge (13.6 ns), and the CW vortex finally forms. The simulation results demonstrate that the effect of the stray field on the dynamic process of vortex creation can be manipulated by the applied control field and that the finally created vortex structure is consequently controlled.
This proposed approach was also confirmed experimentally. Figure 5 shows a series of images for in-plane domain structures observed in an isolated disk (a) and in disks within an array of d=201 nm after their relaxation from the saturation state to the remanent state without and with application of the control field of +30 mT and −30 mT, respectively. The positive Hcontrol was applied to an isolated disk to mimic the stray field existing in the arrays, and the negative Hcontrol was applied to the disks within the array to compensate the effect of the stray field induced by the adjacent disks. We applied Hcontrol with the same external field magnet used in saturation of the disks. To reproduce the procedures performed in the simulations, Hcontrol was applied immediately after the saturation field of +100 mT was turned off, and the finally created vortex structures were observed after turning off Hcontrol. Within three repeated measurements, as shown in Figure 5, by applying Hcontrol during the formation process of vortex structure, the created circularity switches from CW (c=1) to CCW (c=−1) in the isolated disk and CCW (c=−1) to CW (c=1) in disks within the array, although a few exceptions could also be observed occasionally, in good agreement with the simulation results. In the experiment, Hcontrol stronger than 10 mT was preferred to reliably manipulate the stray field effect. It is thought that the stray field from neighboring disks in the array might be not exactly 10 mT in all cases but exceeds 10 mT in real samples with non-ideal geometries. We also found that the reliability for control of the vortex structure using Hcontrol is improved as the strength of the control field increases. Based on 20 repeated measurements, it was verified that reliability for the control of circularity can exceed 80% with Hcontrol=±50 mT. In this manner, for both an isolated disk and a disk within an array, the circularity can be simply controlled by turning the additional Hcontrol on or off, without any need to alter any aspects of array geometry such as the interdisk distance. Moreover, this method offers the possibility of selective control of specific vortex structures in closely packed disks with a simple electrode architecture, thereby also enabling local reconfiguration of magnetic vortices in the disk arrays. By applying current through an electrode during the relaxation of the disks from the saturation state to the remanent state, circularity is controllable using the Oersted field thus generated. The Oersted field induces a control-field effect equal to that shown in Figures 4b and 5, and the latter field can control the stray field from the adjacent disks within the arrays. Any type of electrode is applicable, although the field generated must be sufficiently strong to offset the effect of the stray field that already exists within the arrays.
MTXM images of finally formed circularities in the positive field sequence (+100 mT to 0 mT) without and with the control field of Hcontrol=+30 mT and −30 mT applied during vortex formation in an isolated disk (a) and in disks within an array of d=201 nm (b), respectively. The dimensions of the disks are 2R=1 μm, h=40 nm and r=100 nm (~0.2R), which are nearly equal to those (2R=999 nm, h=40 nm and r=99 nm (~0.2R)) of the disk in the simulations.
Conclusion
We report that simultaneous control of vortex circularity and polarity can be achieved using a simple procedure that applies an in-plane magnetic field, and the reliability of this approach can be enhanced with optimized geometry of the asymmetric disk arrays. Because reliable and simultaneous control of c and p could be crucially beneficial to effective reconfiguration of magnetic vortex structures within arrays, this work advances the potential for applications of magnetic vortices in advanced magnetic nanotechnologies.
References
Shinjo, T., Okuno, T., Hassdorf, R., Shigeto, K. & Ono, T. Magnetic vortex core observation in circular dots of permalloy. Science 289, 930–932 (2000).
Wachowiak, A., Wiebe, J., Bode, M., Pietzsch, O., Morgenstern, M. & Wiesendanger, R. Direct observation of internal spin structure of magnetic vortex cores. Science 298, 577–580 (2002).
Tanigaki, T., Takahashi, Y., Shimakura, T., Akashi, T., Tsuneta, R., Sugawara, A. & Shindo, D. Three-dimensional observation of magnetic vortex cores in stacked ferromagnetic discs. Nano Lett. 15, 1309–1314 (2015).
Fischer, P., Im, M.-Y., Kasai, S., Yamada, K., Ono, T. & Thiaville, A. X-ray imaging of vortex cores in confined magnetic structures. Phys. Rev. B 83, 212402 (2011).
Adolff, C. F., Hänze, M., Pues, M., Weigand, M. & Meier, G. Gyrational modes of benzenelike magnetic vortex molecules. Phys. Rev. B 92, 024426 (2015).
Behncke, C., Hänze, M., Adolff, C. F., Weigand, M. & Meier, G. Band structure engineering of two-dimensional magnonic vortex crystals. Phys. Rev. B 91, 224417 (2015).
Im, M.-Y., Fischer, P., Yamada, K., Sato, T., Kasai, S., Nakatani, Y. & Ono, T. Symmetry breaking in the formation of magnetic vortex states in a permalloy nanodisk. Nat. Commun 3, 983 (2012).
Van Waeyenberge, B., Puzic, A., Stoll, H., Chou, K. W., Tyliszczak, T., Hertel, R., Fahnle, M., Bruckl, H., Rott, K., Reiss, G., Neudecker, I., Weiss, D., Back, C. H. & Schutz, G. Magnetic vortex core reversal by excitation with short bursts of an alternating field. Nature 444, 461–464 (2006).
Mitin, D., Nissen, D., Schädlich, P., Arekapudi, S. S. P. K. & Albrecht, M. Single vortex core recording in a magnetic vortex lattice. J. Appl. Phys. 115, 063906 (2014).
Han, D. S., Vogel, A., Jung, H., Lee, K. S., Weigand, M., Stoll, H., Schutz, G., Fischer, P., Meier, G. & Kim, S. K. Wave modes of collective vortex gyration in dipolar-coupled-dot-array magnonic crystals. Sci. Rep. 3, 2262 (2013).
Sugimoto, S., Fukuma, Y., Kasai, S., Kimura, T., Barman, A. & Otani, Y. Dynamics of coupled vortices in a pair of ferromagnetic disks. Phys. Rev. Lett. 106, 197203 (2011).
Vogel, A., Kamionka, T., Martens, M., Drews, A., Chou, K. W., Tyliszczak, T., Stoll, H., Van Waeyenberge, B. & Meier, G. Coupled vortex oscillations in spatially separated permalloy squares. Phys. Rev. Lett. 106, 137201 (2011).
Jung, H., Choi, Y.-S., Lee, K.-S., Han, D.-S., Yu, Y.-S., Im, M.-Y., Fischer, P. & Kim, S.-K. Logic operations based on magnetic-vortex-state networks. ACS Nano 6, 3712–3717 (2012).
Kumar, D., Barman, S. & Barman, A. Magnetic vortex based transistor operations. Sci. Rep. 4, 4108 (2014).
Sun, L., Cao, R. X., Miao, B. F., Feng, Z., You, B., Wu, D., Zhang, W., Hu, A. & Ding, H. F. Creating an artificial two-dimensional Skyrmion crystal by nanopatterning. Phys. Rev. Lett. 110, 167201 (2013).
Gilbert, D. A., Maranville, B. B., Balk, A. L., Kirby, B. J., Fischer, P., Pierce, D. T., Unguris, J., Borchers, J. A. & Liu, K. Realization of ground-state artificial skyrmion lattices at room temperature. Nat. Commun. 6, 8462 (2015).
Miao, B. F., Sun, L., Wu, Y. W., Tao, X. D., Xiong, X., Wen, Y., Cao, R. X., Wang, P., Wu, D., Zhan, Q. F., You, B., Du, J., Li, R. W. & Ding, H. F. Experimental realization of two-dimensional artificial skyrmion crystals at room temperature. Phys. Rev. B 90, 174411 (2014).
Li, J., Tan, A., Moon, K. W., Doran, A., Marcus, M. A., Young, A. T., Arenholz, E., Ma, S., Yang, R. F., Hwang, C. & Qiu, Z. Q. Tailoring the topology of an artificial magnetic skyrmion. Nat. Commun. 5, 4704 (2014).
Streubel, R., Kronast, F., Rößler, U. K., Schmidt, O. G. & Makarov, D. Reconfigurable large-area magnetic vortex circulation patterns. Phys. Rev. B 92, 104431 (2015).
Martín, J. I., Vélez, M., Hoffmann, A., Schuller, I. K. & Vicent, J. L. Artificially induced reconfiguration of the vortex lattice by arrays of magnetic dots. Phys. Rev. Lett. 83, 1022 (1999).
Hertel, R., Gliga, S., Fahnle, M. & Schneider, C. M. Ultrafast nanomagnetic toggle switching of vortex cores. Phys. Rev. Lett. 98, 117201 (2007).
Yu, Y.-S., Lee, K.-S., Jung, H., Choi, Y.-S., Yoo, M.-W., Han, D.-S., Im, M.-Y., Fischer, P. & Kim, S.-K. Polarization-selective vortex-core switching by tailored orthogonal Gaussian-pulse currents. Phys. Rev. B 83, 174429 (2011).
Bohlens, S., Krger, B., Drews, A., Bolte, M., Meier, G. & Pfannkuche, D. Current controlled random-access memory based on magnetic vortex handedness. Appl. Phys. Lett. 93, 142508 (2008).
Kimura, T., Otani, Y., Masaki, H., Ishida, T., Antos, R. & Shibata, J. Vortex motion in chilarity-controlled pair of magnetic disks. Appl. Phys. Lett. 90, 132501 (2007).
Huang, L., Schofield, M. A. & Zhu, Y. Control of double-vortex domain configurations in a shape-engineered trilayer nanomagnet system. Adv. Mater. 22, 492–495 (2010).
Wu, K.-M., Horng, L., Wang, J.-F., Wu, J.-C., Wu, Y.-H. & Lee, C.-M. Influence of asymmetry on vortex nucleation and annihilation in submicroscaled permalloy disk array. Appl. Phys. Lett. 92, 262507 (2008).
Schneider, M., Hoffmann, H. & Zweck, J. Magnetic switching of single vortex permalloy elements. Appl. Phys. Lett. 79, 3113 (2001).
Dumas, R. K., Gilbert, D. A., Eibagi, N. & Liu, K. Chirality control via double vortices in asymmetric co dots. Phys. Rev. B 83, 060415 (2011).
Giesen, F., Podbielski, J., Botters, B. & Grundler, D. Vortex circulation control in large arrays of asymmetric magnetic rings. Phys. Rev. B 75, 184428 (2007).
Haldar, A. & Adeyeye, A. O. Vortex chirality control in circular disks using dipole-coupled nanomagnets. Appl. Phys. Lett. 106, 032404 (2015).
Uhlir, V., Urbanek, M., Hladik, L., Spousta, J., Im, M. Y., Fischer, P., Eibagi, N., Kan, J. J., Fullerton, E. E. & Sikola, T. Dynamic switching of the spin circulation in tapered magnetic nanodisks. Nat. Nanotechnol. 8, 341–346 (2013).
Jaafar, M., Yanes, R., Perez de Lara, D., Chubykalo-Fesenko, O., Asenjo, A., Gonzalez, E. M., Anguita, J. V., Vazquez, M. & Vicent, J. L. Control of the chirality and polarity of magnetic vortices in triangular nanodots. Phys. Rev. B 81, 054439 (2010).
Shimon, G., Ravichandar, V., Adeyeye, A. O. & Ross, C. A. Simultaneous control of vortex polarity and chirality in thickness-modulated [Co/Pd]n/Ti/Ni80Fe20 disks. Appl. Phys. Lett. 105, 152408 (2014).
Fischer, P., Kim, D.-H., Chao, W., Liddle, J. A., Anderson, E. H. & Attwood, D. T. Soft X-ray microscopy of nanomagnetism. Mater. Today 9, 26–33 (2006).
Donahue, M. J. & Porter, D. G. OOMMF User’s Guide Version 1.0 Interagency Report NISTIR 6376, National Institute of Standards and Technology: Gaitherburg, MD, (1999).
Landau, L. D. & Lifshitz, E. M. Theory of the dispersion of magnetic permeability in ferromagnetic bodies. Phys. Z. Sowjetunion 8, 153 (1935).
Gilbert, T. L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 40, 3443–3449 (2004).
Brown, W. F. Thermal fluctuations of a single-domain particle. Phys. Rev. 130, 1677–1686 (1963).
Shpyrko, O. G., Isaacs, E. D., Logan, J. M., Feng, Y., Aeppli, G., Jaramillo, R., Kim, H. C., Rosenbaum, T. F., Zschack, P., Sprung, M., Narayanan, S. & Sandy, A. R. Direct measurement of antiferromagnetic domain fluctuations. Nature 447, 68–71 (2007).
Im, M.-Y., Fischer, P., Kim, D.-H., Lee, K.-D., Lee, S.-H. & Shin, S.-C. Direct real-space observation of stochastic behavior in domain nucleation process on a nanoscale. Adv. Mater. 20, 1750–1754 (2008).
Aron, C., Barci, D. G., Cugliandolo, L. F., Arenas, Z. G. & Lozano, G. S. Magnetization dynamics: path-integral formalism for the stochastic Landau-Lifshitz-Gilbert equation. J. Stat. Mech. 2014, 09008 (2014).
Kakazei, G. N., Ilyn, M., Chubykalo-Fesenko, O., Gonzalez, J., Serga, A. A., Chumak, A. V., Beck, P. A., Laege, B., Hillebrands, B. & Guslienko, K. Y. Slow magnetization dynamics and energy barriers near vortex state nucleation in circular permalloy dots. Appl. Phys. Lett. 99, 052512 (2011).
Im, M.-Y., Lee, K.-S., Vogel, A., Hong, J.-I., Meier, G. & Fischer, P. Stochastic formation of magnetic vortex structures in asymmetric disks triggered by chaotic dynamics. Nat. Commun. 5, 5620 (2014).
Acknowledgements
This work was supported by the National Research Foundation (NRF) of Korea funded by the Ministry of Education, Science and Technology (MEST) (2012K1A4A3053565, 2014R1A2A2A01003709, 2015M3D1A1070465 and 2016K1A3A7A09005336), by the KIST-UNIST partnership program (1.160097.01/2V05150). Work at the ALS was supported by the Director, Office of Science, Office of Basic Energy Sciences, Scientific User Facilities Division of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. PF acknowledges support by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC02-05CH11231 within the Non-Equilibrium Magnetic Materials Program (MSMAG). AV and GM acknowledge financial support from the Deutsche Forschungsgemeinschaft via SFB 668 ‘Magnetism from the Single Atom to the Nanostructure’, via Graduiertenkolleg 1286 ‘Functional Metal-Semiconductor Hybrid Systems’, and via excellence cluster ‘The Hamburg Centre for Ultrafast Imaging—Structure, Dynamics and Control of Matter on the Atomic Scale’.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Im, MY., Fischer, P., Han, HS. et al. Simultaneous control of magnetic topologies for reconfigurable vortex arrays. NPG Asia Mater 9, e348 (2017). https://doi.org/10.1038/am.2016.199
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/am.2016.199