Abstract
Perovskite manganites exhibit fascinating transport and magnetic properties, essential for fundamental research and applications. With the development of thin film technologies, more exotic properties have been observed in doped-manganites over a wide range of temperature. Unraveling the interplay of spin, charge and orbital degrees of freedom that drives exotic, macroscopic properties is therefore crucial for the understanding of strongly correlated electron systems. Here, using a combination of transport, spectroscopic ellipsometry, X-ray absorption spectroscopy and X-ray magnetic circular dichroism, we observe two concomitant electronic and magnetic phases (insulating paramagnetic phase for T>195 K and insulating canted-ferromagnetic for T<140 K) with an intermediate metal-like state in ultra-thin La0.7Sr0.3MnO3 (LSMO) film on DyScO3 substrate. Surprisingly, the O2p-Mn3d hybridization strength reduces with decreasing temperature, driving the system more insulating and ferromagnetic. The Jahn–Teller effect weakens markedly within the intermediate temperature range, making the system more metal-like. We also apply this comprehensive method to a LSMO film on SrTiO3 substrate for comparison. Our study reveals that the interplay of the O2p-Mn3d hybridization and the dynamic Jahn–Teller splitting controls the macroscopic transport and magnetic properties in ultra-thin manganites.
Similar content being viewed by others
Introduction
Perovskite manganites exhibit fascinating transport and magnetic properties, essential for fundamental research and applications.1, 2, 3, 4, 5, 6, 7 In particular, with the development of thin film nanoscale technologies, more exotic properties have been observed in doped-manganite thin films over a wide range of temperature.8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 However, the origin of many fundamental phenomena remains unclear. For instance, it has been recently shown that doped-manganite ultra-thin films have anomalous transport anisotropic properties, and such complex phenomena could not be explained with a strain effect alone.20 This raises an important, fundamental question of the role of spin, charge and orbital to macroscopic properties in doped-manganite ultra-thin films and strongly correlated electron systems.
Here, we design a new, unique approach to unravel the detailed evolution of electronic and spin structures and their relationship to macroscopic transport and magnetic properties versus temperature. A doped-manganite, La0.7Sr0.3MnO3 (LSMO) ultra-thin film on a DyScO3 (DSO) substrate (LSMO/DSO) is chosen as a model system. Using a combination of temperature-dependent spectroscopic ellipsometry, X-ray absorption spectroscopy (XAS), and X-ray magnetic circular dichroism (XMCD) both at O K-edge and Mn L3,2-edges as well as transport measurements, we show for the first time how the interplay of hybridization, orbital occupancy and spin controls the macroscopic properties. Two concomitant electronic and magnetic phases (insulating paramagnetic phase for T>195 K and insulating canted-ferromagnetic for T<140 K) with an intermediate metal-like state are observed. Surprisingly, the O2p-Mn3d hybridization strength reduces with decreasing temperature, driving the system to become more insulating-like and ferromagnetic. The Jahn–Teller effect weakens markedly within the intermediate temperature range, turning the system into a metal-like state. From our measurements, the temperature-dependent O2p-Mn3d hybridization strength, the energy splitting of eg by the Jahn–Teller effect and its band width are extracted. From these we propose the temperature-dependent density of states of the system.
To further demonstrate how our comprehensive methodology works, we also present a study on LSMO ultra-thin films on SrTiO3 substrates (LSMO/STO) for comparison. We observe that LSMO/STO behaves differently from that on LSMO/DSO, despite both being under tensile strain, of similar thickness and the same chemical doping/stoichiometry. Here, although the O2p-Mn3d hybridization strength increases with decreasing temperature, our similar scenario explains well the observed macroscopic properties.
Materials and methods
Samples growth
High-quality epitaxial LSMO thin films are grown by pulsed laser deposition on atomically smooth [110]-orthorhombic oriented DSO and [001]-cubic oriented STO single-crystal substrate.20 The laser pulse (248 nm) energy density was ~2 J cm-1 and the repetition rate was 3 Hz. The growth was carried out under 200 mTorr oxygen partial pressure at 800 °C and the growth rate was ~0.8 nm min-1.
High-resolution X-ray diffractometry and structure characterization
The crystallographic structure of LSMO films on DSO and STO substrates is characterized by high-resolution X-ray diffractometry in the X-ray Demonstration and Development beamline at the Singapore Synchrotron Light Source. High-resolution X-ray diffractometry studies reveal a perfectly coherent interface between the film and substrate (see Supplementary Figures 1, 2 and 3). The measured lattice constants of LSMO film (on DSO) are monoclinic a=0.3938(3) nm, b=0.3955(3) nm, c=0.3831(1) nm, β=92.79(8)°. The thickness is estimated to be 12.6 nm. The larger lattice constant of the DSO substrate leads to tensile strain in the film, reducing the c/a ratio of LSMO to 0.968. Meanwhile, for the LSMO/STO sample, we obtained a value of c/a of 0.995 (<1). This system is also under tensile strain (see Supplementary information for details).
Electrical measurements
In-plane transport properties of the films are investigated using a low–temperature probe station system at temperatures ranging from 80 to 300 K. Pt electrodes with dimensions of 0.4 mm × 0.8 mm are deposited on the film (see Supplementary Figure 4a) through a shadow mask.
Spectroscopic ellipsometry measurements and optical conductivity
We use a spectroscopic ellipsometer with a photon energy of 0.55–6 eV to measure the ellipsometry parameters Ψ (the ratio between the amplitude of p- and s-polarized reflected light) and Δ (the phase difference between of p- and s-polarized reflected light) with a 70° incident angle and a 45° polarizer angle (see Supplementary Figure 4b). The dielectric function and optical conductivity (σ1) have been extracted from the parameters Ψ and Δ by utilizing an air/LSMO/DSO multilayer model (see supplementary information for details)22. The σ1 at 0 eV can be estimated from dc conductivity in Figure 1a. The σ1 at between 0 and 0.55 eV are estimated using linear interpolation.23
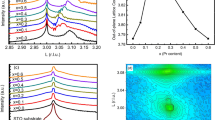
Transport and spectroscopic ellipsometry on ultra-thin La0.7Sr0.3MnO3 film. (a) Resistivity (ρ) versus temperature curve for the La0.7Sr0.3MnO3 film on DyScO3 substrate (LSMO/DSO) along [001]-orthorhombic direction for DyScO3. Two transition temperatures are observed, Tmin (~140 K) and Tmax (~195 K). Region-1: T>Tmax; Region-2 (or intermediate): Tmin<T<Tmax; Region-3: T<Tmin. The inset is the resistivity vs temperature on log scale. (b) Optical conductivity (σ1(ω)) from 0 to 6 eV as a function of temperature for ultra-thin LSMO/DSO film. The σ1 at energy between 0 eV (estimated from the conductivity in (a) and 0.55 eV) is estimated using a linear interpolation. The two light-green color arrows point to the energy position of Mn-eg→ Mn-eg transition (~1 eV) and of charge transfer O2p→ Mn-eg transition (~1.4 eV) at 300 K. The inset is the imaginary part of the dielectric function ɛ2(ω) from 0.55 to 2 eV as a function of temperature. The different color arrows point to the energy position of the eg–eg transition at 80 K (red), 160 K (purple) and 300 K (light green). (c) The number of effective charge (Neff) as a function of temperature for two different regions: 0–1.8 and 1.8–6 eV. (d) Energy position of the Jahn–Teller peak (eg–eg transition) versus temperature obtained from b and e) Change of optical conductivity Δσ1(T) defined as σ1(T)-σ1(300 K) for LSMO/DSO. (f) Integrated spectral weight  defined as
defined as  in different spectral regions: SW1 (0–1.8 eV), SW2 (1.8–6 eV), and total energy range SWtotal (0–6 eV). T is temperature (Kelvin).
in different spectral regions: SW1 (0–1.8 eV), SW2 (1.8–6 eV), and total energy range SWtotal (0–6 eV). T is temperature (Kelvin).
X-ray absorption spectroscopy
The O K-edge absorption spectra in the energy range 520–580 eV and Mn L-edge absorption spectra in the energy range 630–680 eV were obtained using linearly polarized XAS from the Surface, Interface and Nanostructure Science beamline at Singapore Synchrotron Light Source, using a total electron yield detection method. The incidence angle (θ) of X-rays refers to the normal of the sample surface, which was varied by rotating the polar angle of the sample. The E||[001]-orthorhombic direction spectra were measured in a normal-incident alignment (θ=0°) (see Supplementary Figure 4a). The temperature was varied between 80 and 300 K. The spectra were normalized to the integrated intensity between 565and 580 eV for O1s spectra and between 670 and 680 eV for Mn2p spectra after subtracting an energy-independent background.
X-ray linear dichroism measurements
For Mn, the  and
and  orbitals have lobes pointing parallel and perpendicular to the ab plane, respectively. X-ray linear dichroism measurements can probe the occupancy of the
orbitals have lobes pointing parallel and perpendicular to the ab plane, respectively. X-ray linear dichroism measurements can probe the occupancy of the  and
and  orbitals using linearly polarized light aligned to the out-of-plane (grazing incidence, E~||c) and in-plane (normal incidence, E||a) directions (Supplementary Figure 4a). The X-ray linear dichroism measurements result shows a near temperature independence at 80 and 300 K (Supplementary Figure 8). Smaller absorption for in-plane polarization spectra suggests more out-of-plane empty states in the 3d eg band (a higher occupancy of in-plane orbitals). The spectral difference (I(E||a)-I(E||c), linear dichroism) implies a preferential occupancy of the
orbitals using linearly polarized light aligned to the out-of-plane (grazing incidence, E~||c) and in-plane (normal incidence, E||a) directions (Supplementary Figure 4a). The X-ray linear dichroism measurements result shows a near temperature independence at 80 and 300 K (Supplementary Figure 8). Smaller absorption for in-plane polarization spectra suggests more out-of-plane empty states in the 3d eg band (a higher occupancy of in-plane orbitals). The spectral difference (I(E||a)-I(E||c), linear dichroism) implies a preferential occupancy of the  orbital at both 80 and 300 K. The result is in good agreement with the theoretically calculated result for LSMO film under tensile strain.18, 24
orbital at both 80 and 300 K. The result is in good agreement with the theoretically calculated result for LSMO film under tensile strain.18, 24
X-ray magnetic circular dichroism measurements
The XMCD signal is the difference between absorption spectra obtained with a +1T and a -1T magnetic field, which was set parallel to the X-ray beam direction using plus helicities of circular polarized light. The grazing-incident spectra were measured at θ=60° (see Supplementary Figure 4a), which is estimated as the magic angle.25, 26 The degree of circular polarization (Pc) was calculated to be 88%.
Results
Transport properties
The temperature-dependent resistivity of the LSMO film along the in-plane [001]-orthorhombic direction (for the DSO substrate) reveals unusual behavior with two transition-temperatures, Tmin (~140 K) and Tmax (~195 K) (Figure 1a). Insulating behavior is observed both above Tmax and below Tmin, whereas a metal-like state appears in between (at the intermediate temperature region). To reveal the microscopic mechanism behind these transitions, we use a combination of techniques including temperature-dependent spectroscopic ellipsometry, XAS and XMCD to probe the detailed electronic and spin structures directly.
Electronic properties
Let us first discuss results from spectroscopic ellipsometry measurements (see Figures 1b–f). The spectroscopic ellipsometer reveals optical conductivity (σ1(ω)) (see Methods), which directly connects to the electronic density of states (as discussed later). As shown in previous studies, by measuring σ1(ω) in a broad energy range, one can find the origin of charges that contribute to transport measurements.22, 23 Figure 1b displays a combination of σ1(ω) spectra (from 0.55 to 6 eV) and transport measurements (0 eV), showing strong temperature dependence of σ1(ω) in a broad energy range. An enhancement of spectral weight of σ1(ω) below 1.8 eV on cooling is coming from spectral weight above 1.8 eV. This implies the importance of electronic structure of higher energy bands determining low-energy transport properties. This will be clear in the following detailed analysis. For simplicity, σ1(ω) is divided into two regions: below 1.8 eV (low-energy region, SW1 for spectral weight) and above 1.8 eV (high-energy region, SW2 for spectral weight). The number of effective charges (Neff) can be quantified as follows:

In our measured spectral energy range, we find that the total number of charges is nearly constant (within ~1.2%) as a function of temperature (Figure 1c). As charge conservation has to be fulfilled, this is important to validate our next analysis.22, 23 As shown in Figure 1c, the enhancement of Neff (T) in SW1 as temperature decreases is closely accompanied by the reduction of Neff (T) in SW2. This directly tells us that the low-energy transport property is determined by electronic bands at higher energy bands.
We inspect now in more detail the low-energy region. Two peaks are observed at ~1.4 and ~1 eV, with different temperature-dependent behavior (see also inset of Figure 1b). The ~1.4 eV peak is almost temperature-independent. This peak has been ascribed to the O2p → Mn-eg excitations.27, 28 The ~1 eV peak, on the other hand, increases its intensity markedly as the temperature decreases. Interestingly, the position of this peak shows a red-shift between Tmax and Tmin, and remains almost unchanged outside this region (Figures 1b and e). According to the above observations and comparing with previous studies, this ~1 eV peak is assigned to the Mn-eg→Mn-eg (or eg–eg) transitions with a parallel spin, which is directly related to the Jahn–Teller effect of the Mn3d states.28, 29, 30, 31 The red-shift of the ~1 eV peak shows that the dynamic Jahn–Teller splitting energy is significantly reduced as the temperature decreases and this happens in the intermediate temperature region (see Figure 1d). Although the origin of the sudden decrease in the Jahn–Teller splitting energy is not clear at the moment, as discussed later, we show that the interplay between the dynamic Jahn–Teller splitting and hybridizations is responsible for the macroscopic property in the intermediate state. Together with the transport data, it is clear that the increase of SW1 does not develop into a Drude response, instead it reveals the dynamics of the eg–eg transitions, yielding to insulating behavior at lower temperature. The features in the high-energy region (above 1.8 eV) in Figure 1b arise from transitions between O2p and Mn 3d as well as between lower and upper Hund’s rule split bands.29, 32
Owing to the Kramers–Kronig transformation, the pre-eminence of the spectroscopic ellipsometry approach allows one to measure the charge transfer accurately using the optical f-sum rule.22, 23 As the temperature decreases, an increase of SW1 by as much as ~33% below Tmax is accompanied by a decrease of SW2 spanning an energy range up to 6 eV (Figure 1f). It is found that the total spectral weight (or Neff) is nearly conserved throughout the whole-temperature range (Figure 1f (or Figure 1c)). The occurrence of spectral-weight transfer in such a broad energy range as a function of temperature is an important signature of strong electronic correlations and hybridization strength that drives the system from one phase to another.23, 33, 34 Later, it is shown that the spectral weight transfer is due to marked changes of hybridization strength measured using temperature-dependent XAS.
Hybridizations and orbital occupancy
We next identify details of the hybridization strength, in particular O2p-Mn3d hybridization, and orbital occupancies as functions of temperature and later explain their intimate connection with macroscopic properties. These can be probed directly using element-specific XAS as a function of temperature.33 Our main observation is the strong temperature-dependent XAS at O K-edge for E||[001]-orthorhombic direction (Figure 2a). The change of XAS, Δμ(T), is defined as μ(T)—μ(300 K), where μ(T) is the XAS at temperature T. Because the O K-edge XAS reveals transitions from O1s to unoccupied states related to O2p states hybridized with metal states, it is directly related to the corresponding hybridization strengths. In Figure 2a, the O K-edge spectra is divided into three regions: (1) a pre-edge region attributed to O2p-Mn3d hybridization (527–533.5 eV); (2) a broad structure associated with the hybridization of O2p-La5d and O2p-Sr4d states (533.5–538.5 eV); and (3) a broad feature due to O2p hybridized with higher energy metal states, for example, O2p-Mn4s,p and O2p-La6s,p (538.5–548.5 eV). The observed strong reduction of spectral weight in the pre-edge region as temperature decreases corresponds to a decrease of O2p-Mn3d hybridization strength.35
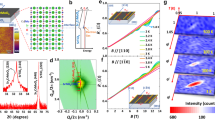
X-ray absorption spectra and magnetic structure on ultra-thin La0.7Sr0.3MnO3 film. (a) O K-edge and (b) Mn L3,2-edge X-ray absorption spectra of the La0.7Sr0.3MnO3 film on DyScO3 substrate as a function of temperature for E||[001]-orthorhombic direction. The change of absorption spectra Δμ(T) defined as μ(T)-μ(300 K) is presented below each spectrum. μ(T) is the absorption spectrum at temperature T. (c) Integrated spectral weight  defined as
defined as  in the energy range of 527–533.5 eV for O K-edge spectra and in the energy range of 636–649 eV for Mn L3-edge spectra. (d) The exchange spin coupling (Jex) versus hybridization (hopping) between the O2p and Mn3d orbitals (tpd). For double exchange, JDE∝tpd. For super-exchange, JSE∝(tpd)2/U, where U is a Hubbard energy for Mn.
in the energy range of 527–533.5 eV for O K-edge spectra and in the energy range of 636–649 eV for Mn L3-edge spectra. (d) The exchange spin coupling (Jex) versus hybridization (hopping) between the O2p and Mn3d orbitals (tpd). For double exchange, JDE∝tpd. For super-exchange, JSE∝(tpd)2/U, where U is a Hubbard energy for Mn.
In contrast, the XAS at Mn-L3,2 edges (Figure 2b) are nearly temperature-independent. At the edges, they reflect Mn2pj→Mn3d transitions, thus they are directly related to the occupancy of Mn3d orbitals.35 The spectra show two broad separated features at ~642 and ~653 eV owing to strong spin-orbit coupling that splits the Mn2pj core level with j=3/2 and 1/2.35 This implies that the change of Mn3d occupancy Δμ(T) is negligible as a function of temperature. This is further supported with temperature-dependent X-ray linear dichroism measurements (Supplementary Figure 9). The relative strength of O2p-Mn3d hybridization (from the pre-edge region in the O K-edge XAS in Figure 2a) and the occupancy of Mn3d (from the Mn L3,2-edge XAS in Figure 2b) as functions of temperature are summarized in Figure 2c. We argue that the spectral weight transfer observed in spectroscopic ellipsometry is due to the change of O2p-Mn3d hybridization strength, in which hybridization together with dynamic Jahn–teller effects control anomalous transport and magnetic properties as discussed later.
Magnetic properties
The magnetic behavior of LSMO/DSO is probed by element-specific temperature-dependent XMCD at the Mn L3,2-edges and O K-edge (see Methods). Figure 3 shows XMCD at Mn L3,2-edges and O K-edge at selected temperatures and calculated magnetic moments (spin, orbital and total) (see also supplementary Figure 11 and Supplementary Table 1). At 300 K, there is no observable XMCD signal. The system can be considered to be in a paramagnetic phase. On cooling down to 160 K, where the system behaves as metal-like, the XMCD signal appears. This suggests the appearance of a net magnetic moment. At 80 K, the film displays a further enhanced XMCD signal, only at Mn L3,2-edges. As XMCD contains both net spin (mspin) and orbital (morb) magnetic moments, one can estimate the total magnetic moment, mtotal=mspin+morb as shown in Figure 3d.36, 37 Using the angle-dependent XMCD sum rule,25, 36, 37 mtotal is found to be 0.202 μB at 160 K and 1.201 μB at 80 K (see supplementary information for details). We find that the total magnetic moment of LSMO/DSO at 80 K is less than half of that of ferromagnetic bulk LMSO or other LSMO films.38, 39, 40 Note that such transport and magnetic properties cannot be explained by the strain effect.
X-ray magnetic circular dichroism (XMCD) on ultra-thin La0.7Sr0.3MnO3 film. Temperature-dependent XMCD of the La0.7Sr0.3MnO3 film on DyScO3 substrate at (a, c) Mn L3,2-edges and (b) O K-edge at selected temperature for grazing incident (θ=60°). μ+ and μ− are X-ray absorption spectra with two opposite magnetization directions relate to the fixed photon helicity, and the corresponding XMCD signal defined as μ+–μ−. (d) Magnetic moment of spin (mspin), orbital (morb) and total (mtotal) is calculated from XMCD at Mn L3,2 as a function of temperature.
Discussion
By combining spectroscopic ellipsometry and XAS, we uncover the following facts. As the temperature decreases, the O2p-Mn3d hybridization strength (tpd) decreases monotonically (as shown by the O K-edge XAS), whereas the occupancy of Mn3d remains almost unchanged (as shown by the Mn L3,2-edges XAS). The Jahn–Teller splitting energy of the eg bands remains relatively unchanged at high and low temperatures, but drops markedly between Tmin and Tmax (as shown by spectroscopic ellipsometry in Figures 1b and d).
The anomalous transport behavior (Figure 1a) can now be explained (Figure 4). The p-d hybridization strength (tpd) determines the bandwidths (Γ) of the two Jahn–Teller-split eg bands, between which the Fermi level is located. For T>Tmax (see Figure 4a), as T decreases tpd decreases causing Γ to decrease, which in turn decreases the density of states at the Fermi level (DOS(EF)). As resistivity (ρ) is inversely proportional to this quantity, thus ρ increases. For Tmin<T<Tmax (see Figure 4b), while tpd keeps decreasing, the Jahn–Teller effect weakens more rapidly (as indicated by the abrupt decrease in the Jahn–Teller splitting energy (EJT)), causing the DOS(EF) to increase, thus ρ decreases, transforming the system to metal-like. For T<Tmin (see Figure 4c), tpd continues to decrease, whereas EJT is almost unchanged, causing the DOS(EF) to decrease, thus ρ increases, turning the system back to insulating. Clearly that it is the competition between O2p-Mn3d hybridization and dynamic Jahn–Teller effect that sparks the non-monotonic temperature-dependent transport behavior. Neither one of them alone can explain the observation.
Electronic structure on ultra-thin La0.7Sr0.3MnO3 film. The schematic of the processes causing the change of the resistivity behavior as temperature decreases, a1, b1, a2, b2, a3 and b3 temperature points are from the three different temperature range (a) Region-1, (b) Region-2 and (c) Region 3 in Figure 1a. The eg states near Fermi level (EF) are split by the Jahn–Teller effect (EJT). The band width (Γ) of the eg states is related to the O2p-Mn3d hybridization tpd. The resistivity (ρ) is roughly inversely proportional to the density of states at the Fermi level (DOS(EF)).
Concomitantly, the change of magnetic behavior as T decreases is also affected by tpd. It is well known that super-exchange (JSE) and double-exchange (JDE) couplings can be related to the hopping parameter (in our case tpd) following  and JDE∝tpd, respectively. This is illustrated by the Jex vs tpd sketch in Figure 2d, demonstrating that antiferromagnetism is favorable for large tpd (high T), whereas ferromagnetism is favorable for small tpd (low T). Although super-exchange normally favors antiferromagnetism and double-exchange favors ferromagnetism41, in their close proximity the competition may lead to a canted-ferromagnetic (or canted-antiferromagnetic) spin arrangement.
and JDE∝tpd, respectively. This is illustrated by the Jex vs tpd sketch in Figure 2d, demonstrating that antiferromagnetism is favorable for large tpd (high T), whereas ferromagnetism is favorable for small tpd (low T). Although super-exchange normally favors antiferromagnetism and double-exchange favors ferromagnetism41, in their close proximity the competition may lead to a canted-ferromagnetic (or canted-antiferromagnetic) spin arrangement.
As discussed above, our XMCD measurement reveals a small net magnetization for the ultra-thin LSMO film on DSO at low temperature. One might think of a phase separation between ferromagnetic and antiferromagnetic or other non-magnetic phases.42, 43 We argue that this is not the case here for the following reasons. First, we do not observe a XMCD signal at the O K-edge (see Supplementary Figure 11), suggesting that the local ferromagnetic regions are not present in our samples. As a comparison, for ferromagnetic bulk LSMO, the dichroism at the O K-edge is significant, emphasizing the importance of the double-exchange mechanism.40 Second, temperature-dependent resistivity measurements on similar LSMO/DSO ultra-thin film show no hysteresis between cooling and heating at the low-temperature region,20 which further supports a single-phase character. Thus, a canted-ferromagnetic (or canted-antiferromagnetic) phase is the most plausible interpretation for the low-temperature magnetic phase of LSMO/DSO ultra-thin films.
Combining the above analyses, we can conclude the following. At T=300 K, the system is paramagnetic owing to the strong thermal fluctuation. Upon cooling, tpd decreases (Figure 2c) accompanied by the appearance of a net magnetic moment (Figures 3b and c and discussion above), whereas the orbital occupancy of Mn3d remains constant (Figure 2c). This suggests that the spins start to align along a certain direction with some degree of canting owing to the competing mechanisms of super-exchange and double exchange. With further cooling down to 80 K, the net magnetic moment increases because JDE becomes more dominant over JSE for lower temperature.
To further support our argument on the necessity of looking at the electronic and spin structures directly using the comprehensive methodology, we also present our study on LSMO ultra-thin films on STO substrates, LSMO/STO (see Supplementary Figure 12). Despite being under tensile strain too, the same chemical composition and very similar film thickness, we find that the strength of p-d hybridization increases as temperature decreases (see Supplementary Figure 12a and the black dot in Supplementary Figure 12b). This is opposite to that observed in LSMO/DSO (see Figure 2a and black dot in Figure 2c), yet it explains well the observed monotonic decrease of the resistivity and increase of magnetization in LSMO/STO as temperature decreases (see Supplementary information for details).
In conclusion, by combining transport, spectroscopic ellipsometry, XAS and XMCD studies, we have revealed clearly the interplay of hybridizations and the dynamic Jahn–Teller effect that determines the macroscopic electronic transport and magnetic properties of LSMO/DSO ultra-thin films. Furthermore, the methodology presented here leading to our conclusion is valuable for the study of other strongly correlated systems.
References
Jonker, G. H. & Van Santen, J. H. Ferromagnetic compounds of manganese with perovskite structure. Physica 16, 337–349 (1950).
Saitoh, E., Okamoto, S., Takahashi, K. T., Tobe, K., Yamamoto, K., Kimura, T., Ishihara, S., Maekawa, S. & Tokura, Y. Observation of orbital waves as elementary excitations in a solid. Nature 410, 180–183 (2001).
Milward, G. C., Calderon, M. J. & Littlewood, P. B. Electronically soft phases in manganites. Nature 433, 607–610 (2005).
Hueso, L. E., Pruneda, J. M., Ferrari, V., Burnell, G., Valdés-Herrera, J. P., Simons, B. D., Littlewood, P. B., Artacho, E., Fert, A. & Mathur, N. D. Transformation of spin information into large electrical signals using carbon nanotubes. Nature 445, 410–413 (2007).
Cheong, S. W. & Mostovoy, M. Multiferroics: a magnetic twist for ferroelectricity. Nat. Mater. 6, 13–20 (2007).
Basov, D. N., Averitt, R. D., van der Marel, D., Dressel, M. & Haule, K. Electrodynamics of correlated electron materials. Rev. Mod. Phys. 83, 471–541 (2011).
Beaud, P., Caviezel, A., Mariager, S. O., Rettig, L., Ingold, G., Dornes, C., Huang, S. W., Johnson, J. A., Radovic, M., Huber, T., Kubacka, T., Ferrer, A., Lemke, H. T., Chollet, M., Zhu, D., Glownia, J. M., Sikorski, M., Robert, A., Wadati, H., Nakamura, M., Kawasaki, M., Tokura, Y., Johnson, S. L. & Staub, U. A time-dependent order parameter for ultrafast photoinduced phase transitions. Nat. Mater. 13, 923–927 (2014).
Izumi, M., Konishi, Y., Nishihara, T., Hayashi, S., Shinohara, M, Kawasaki, M. & Tokura, Y. Atomically defined epitaxy and physical properties of strained La0.6Sr0.4MnO3 films. Appl. Phys. Lett. 73, 2497–2499 (1998).
Sun, J. Z., Abraham, D. W., Rao, R. A. & Eom, C. B. Thickness-dependent magnetotransport in ultrathin manganite films. Appl. Phys. Lett. 74, 3017–3019 (1999).
Bowen, M., Bibes, M., Barthelemy, A., Contour, J.-P., Anane, A., Lemaitre, Y. & Fert, A. Nearly total spin polarization in La2/3Sr1/3MnO3 from tunneling experiments. Appl. Phys. Lett. 82, 233–235 (2003).
Orgiani, P., Petrov, A. Yu., Adamo, C., Aruta, C., Baruta, C., De Luca, G. M., Galdi, A., Polichetti, M., Zola, D. & Maritato, L. In-plane anisotropy in the magnetic and transport properties of manganite ultrathin films. Phys. Rev. B 74, 134419 (2006).
Aruta, C., Ghiringhelli, G., Tebano, A., Boggio, N. G., Brookes, N. B., Medaglia, P. G. & Balestrino, G. Strain induced x-ray absorption linear dichroism in La0.7Sr0.3MnO3 thin films. Phys. Rev. B 73, 235121 (2006).
Thiele, C., Dörr, K., Bilani, O., Rödel, J. & Schultz, L. Influence of strain on the magnetization and magnetoelectric effect in La0.7A0.3MnO3/PMN-PT(001) (A=Sr, Ca). Phys. Rev. B 75, 054408 (2007).
Chakhalian, J., Freeland, J. W., Habermeier, H. U., Cristiani, G., Khaliullin, G., van Veenendaal, M. & Keimer, B. Orbital reconstruction and covalent bonding at an oxide interface. Science 318, 1114–1117 (2007).
Huijben, M., Martin, L. W., Chu, Y.-H., Holcomb, M. B., Yu, P., Rijnders, G., Blank, D. H.A. & Ramesh, R. Critical thickness and orbital ordering in ultrathin La0.7Sr0.3MnO3 films. Phys. Rev. B 78, 094413 (2008).
Lai, K., Nakamura, M., Kundhikanjana, W., Kawasaki, M., Tokura, Y., Kelly, M. A. & Shen, Z. X. Mesoscopic percolating resistance network in a strained manganite thin film. Science 329, 190–193 (2010).
Kourkoutis, L. F., Song, J. H., Hwang, H. Y. & Muller, D. A. Microscopic origins for stabilizing room-temperature ferromagnetism in ultrathin manganite layers. Proc. Natl Acad. Sci. 107, 11682–11685 (2010).
Pesquera, D., Herranz, G., Barla, A., Pellegrin, E., Bondino, F., Magnano, E., Sánchez, F. & Fontcuberta, J. Surface symmetry-breaking and strain effects on orbital occupancy in transition metal perovskite epitaxial films. Nat. Commun. 3, 1189 (2012).
Boschker, H., Verbeeck, Jo, Egoavil, Ricardo, Bals, Sara, Tendeloo, Gustaf van, Huijben, Mark, Houwman, Evert P., Koster, Gertjan, Blank, Dave H.A. & Rijnders, Guus Preventing the reconstruction of the polar discontinuity at oxide heterointerfaces. Adv. Funct. Mater. 22, 2235–2240 (2012).
Wang, B., You, L., Ren, P., Yin, X., Peng, Y., Xia, B., Wang, L., Yu, X., Poh, S. M., Yang, P., Yuan, G., Chen, L., Rusydi, A. & Wang, J. Oxygen-driven anisotropic transport in ultra-thin manganite films. Nat. Commun. 4, 2778 (2013).
Zhai, X., Cheng, L., Liu, Y., Schlepütz, C. M., Dong, S., Li, H., Zhang, X., Chu, S., Zheng, L., Zhang, J., Zhao, A., Hong, H., Bhattacharya, A., Eckstein, J. N. & Zeng, C. Correlating interfacial octahedral rotations with magnetism in (LaMnO3+δ)N/(SrTiO3)N superlattices. Nat. Commun. 5, 4283 (2014).
Asmara, T. C., Annadi, A., Santoso, I., Gogoi, P. K., Kotlov, A., Omer, H. M., Motapothula, M., Breese, M. B., Rübhausen, M., Venkatesan, T., Ariando & Rusydi, A. Mechanisms of charge transfer and redistribution in LaAlO3/SrTiO3 revealed by high-energy optical conductivity. Nat. Commun. 5, 3663 (2014).
Rusydi, A., Rauer, R., Neuber, G., Bastjan, M., Mahns, I., Müller, S., Saichu, P., Schulz, B., Singer, S. G., Lichtenstein, A. I., Qi, D., Gao, X., Yu, X., Wee, A. T.S., Strayganyuk, G., Dörr, K., Sawatzky, G. A., Cooper, S. L. & Rübhausen, M. Metal-insulator transition in manganites: changes in optical conductivity up to 22 eV. Phys. Rev. B 78, 125110 (2008).
Tebano, A., Aruta, C., Sanna, S., Medaglia, P. G., Balestrino, G., Sidorenko, A. A., De Renzi, R., Ghiringhelli, G., Braicovich, G., Bisogni, V. & Brookes, N. B. Evidence of orbital reconstruction at interfaces in ultrathin La0.67Sr0.33MnO3 films. Phys. Rev. Lett. 100, 137401 (2008).
Stöhr, J. & König, H. Determination of spin- and orbital-moment anisotropies in transition metals by angle-dependent X-ray magnetic circular dichroism. Phys. Rev. Lett. 75, 3748–3751 (1995).
Koide, T., Miyauchi, H., Okamoto, J., Shidara, T., Fujimori, A., Amemiya, K., Takeshita, H., Yuasa, S., Katayama, T. & Suzuki, Y. Direct determination of interfacial magnetic moments with a magnetic phase transition in Co nanoclusters on Au(111). Phys. Rev. Lett. 87, 257201 (2001).
Arima, T., Tokura, Y. & Torrance, J. B. Variation of optical gaps in perovskite-type 3d transition-metal oxides. Phys. Rev. B 48, 17006–17009 (1993).
Okimoto, Y., Katsufuji, T., Ishikawa, T., Arima, T. & Tokura, Y. Variation of electronic structure in La1-xSrxMnO3 (0≤x≤0.3) as investigated by optical conductivity spectra. Phys. Rev. B 55, 4206–4214 (1997).
Rauer, R., Rübhausen, M. & Dörr, K. Magnetic-order induced spectral-weight redistribution in La0.7(Sr, Ca)0.3MnO3. Phys. Rev. B 73, 092402 (2006).
Moritomo, Y., Machida, A., Matsuda, K., Ichida, M. & Nakamura, A. Magnetization-dependent behaviors of interband transitions between the exchange-split bands in doped manganite films. Phys. Rev. B 56, 5088–5091 (1997).
Quijada, M., Černe, J., Simpson, J. R., Drew, H. D., Ahn, K. H., Millis, A. J., Shreekala, R., Ramesh, R., Rajeswari, M. & Venkatesan, T. Optical conductivity of manganites: crossover from Jahn-Teller small polaron to coherent transport in the ferromagnetic state. Phys. Rev. B 58, 16093–16102 (1998).
Takenaka, K., Sawaki, Y., Shiozaki, R. & Sugai, S. Electronic structure of the double-exchange ferromagnet La0.825Sr0.175MnO3 studied by optical reflectivity. Phys. Rev. B 62, 13864–13867 (2000).
Meinders, M. B.J., Eskes, H. & Sawatzky, G. A. Spectral-weight transfer: breakdown of low-energy-scale sum rules in correlated systems. Phys. Rev. B 48, 3916–3926 (1993).
Majidi, M. A., Su, H., Feng, Y. P., Rübhausen, M. & Rusydi, A. Theory of high-energy optical conductivity and the role of oxygens in manganites. Phys. Rev. B 84, 075136 (2011).
Abbate, M., de Groot, F. M., Fuggle, J. C., Fujimori, A., Strebel, O., Lopez, F., Domke, M., Kaindl, G., Sawatzky, G. A., Takano, M., Takeda, Y., Eisaki, H. & Uchida, S. Controlled-valence properties of La1-xSrxFeO3 and La1-xSrxMnO3 studied by soft-x-ray absorption spectroscopy. Phys. Rev. B 46, 4511–4519 (1992).
Thole, B. T., Carra, P., Sette, F. & van der Laan, G. X-ray circular dichroism as a probe of orbital magnetization. Phys. Rev. Lett. 68, 1943–1946 (1992).
Carra, P., Thole, B. T., Altarelli, M. & Wang, X. X-ray circular dichroism and local magnetic fields. Phys. Rev. Lett. 70, 694–697 (1993).
Pellegrin, E., Tjeng, L. H., de Groot, F. M.F., Hesper, R., Sawatzky, G. A., Moritomo, Y. & Tokura, Y. Soft X-ray magnetic circular dichroism study of the colossal magnetoresistance compound La1−xSrxMnO3. J. Electron. Spectrosc. Relat. Phenom. 86, 115–118 (1997).
Konishi, Y., Fang, Z., Izumil, M., Manako, T., Kasail, M., Kuwahara, H., Kawasaki, M., Terakura, K. & Tokura, Y. Orbital-state-mediated phase-control of manganites. J. Phys. Soc. Jpn. 68, 3790–3793 (1999).
Koide, T., Miyauchi, H., Okamoto, J., Shidara, T., Sekine, T., Saitoh, T., Fujimori, A., Fukutani, H., Takano, M. & Takeda, Y. Close correlation between the magnetic moments, lattice distortions, and hybridization in LaMnO3 and La1-xSrxMnO3+delta: doping-dependent magnetic circular X-ray dichroism study. Phys. Rev. Lett. 87, 246404 (2001).
de Gennes, P. G. Effects of double exchange in magnetic crystals. Phys Rev 118, 141–154 (1960).
Dagotto, E., Hotta, T. & Moreo, A. Colossal magnetoresistant materials: the key role of phase separation. Phys. Rep. 344, 1–153 (2001).
Burkhardt, M. H., Hossain, M. A., Sarkar, S., Chuang, Y. D., Cruz Gonzalez, A. G., Doran, A., Scholl, A., Young, A. T., Tahir, N., Choi, Y. J., Cheong, S. W., Dürr, H. A. & Stöhr, J. Imaging the first-order magnetic transition in La0.35Pr0.275Ca0.375MnO3. Phys. Rev. Lett. 108, 237202 (2012).
Acknowledgements
This work is supported by Singapore National Research Foundation under its Competitive Research Funding (NRF-CRP 8-2011-06 and NRF2008NRF-CRP002024), MOE-AcRF Tier-2 (MOE2010-T2-2-121) and NUS-YIA. We acknowledge the CSE-NUS computing center for providing facilities for our numerical calculations. The work at Nanyang Technological University is supported by National Research Foundation of Singapore under project NRF-CRP5-2009-04. JW acknowledges support from National Natural Science Foundation of China under the Overseas, Hong Kong & Macau Scholars Collaborated Research Fund (51428201).
Author Contributions
X Yin, XC, NP, XY, DC and AR performed X-ray absorption and XMCD measurements. X Yin, DS and AR performed spectroscopic ellipsometry measurements. JW, PR and LY grew high-quality thin films and performed transport measurements. YP, X Yin and AR performed synchrotron X-ray diffraction and topography measurements. MAM and AR performed theoretical calculations. XYin, MAM, AR analyzed the data. AR wrote the manuscript with the assistance from XYin, MAM, JW and MBHB AR planned and designed a combination of spectroscopic ellipsometry, X-ray absorption and XMCD measurements. AR and JW supervised the project.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies the paper on the NPG Asia Materials website
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Yin, X., Majidi, M., Chi, X. et al. Unraveling how electronic and spin structures control macroscopic properties of manganite ultra-thin films. NPG Asia Mater 7, e196 (2015). https://doi.org/10.1038/am.2015.65
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/am.2015.65
This article is cited by
-
Unrevealing tunable resonant excitons and correlated plasmons and their coupling in new amorphous carbon-like for highly efficient photovoltaic devices
Scientific Reports (2023)
-
Oxygen vacancies effects on phase diagram of epitaxial La1–x Sr x MnO3 thin films
Science China Physics, Mechanics & Astronomy (2017)