Abstract
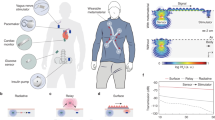
Smart implants are envisioned to revolutionize personal health care by assessing physiological processes, for example, upon wound healing, and communicating these data to a patient or medical doctor. The compactness of the implants is crucial to minimize discomfort during and after implantation. The key challenge in realizing small-sized smart implants is high-volume cost- and time-efficient fabrication of a compact but efficient antenna, which is impedance matched to 50 Ω, as imposed by the requirements of modern electronics. Here, we propose a novel route to realize arrays of 5.5-mm-long normal mode helical antennas operating in the industry-scientific-medical radio bands at 5.8 and 2.4 GHz, relying on a self-assembly process that enables large-scale high-yield fabrication of devices. We demonstrate the transmission and receiving signals between helical antennas and the communication between an antenna and a smartphone. Furthermore, we successfully access the response of an antenna embedded in a tooth, mimicking a dental implant. With a diameter of ~0.2 mm, these antennas are readily implantable using standard medical syringes, highlighting their suitability for in-body implant applications.
Similar content being viewed by others
Introduction
Smart implants are efficient tools for monitoring physiological processes in the human body, which is especially crucial after a surgical treatment. These intrinsically multifunctional devices should sense a signal, process it and communicate it to a patient or her/his medical doctor by, for example, displaying the relevant information on the screen of a smartphone (Figure 1a). For example, for a wound-healing process, the parameters of interest assessed by the implants are the time evolution of the pH,1 local temperature2 or bacteriological infection value.3 Recent developments of low power consumption devices enabled the realization of wireless tissue and in-body implants. The possibility to address implants wirelessly extended their application potential enormously, with numerous systems already available, including drug-delivery platforms,4 cochlear implants,5 pressure monitors in the brain cavity,6 glaucoma sensors,6, 7 retinal implants,6, 8, 9 brain-to-nerve interconnections for cerebral injuries10 and direct control of prostheses.11, 12, 13
Compact helical antenna for implant applications. (a) Concept of a smart implant for in-body applications using the example of a wireless tooth implant. The relevant data, e.g., temperature or pH, are acquired and communicated by the implant to an external device, e.g., a smartphone. (b) For a dental implant, the size of the device is absolutely crucial and cannot exceed 5 × [3 × 2] mm3 (length × cross-section area). (c) The compact helical antenna prepared by strain engineering with a total length of 5.5 mm and a diameter of ~200 μm fits perfectly into a cavity prepared in the model of a tooth (inset). Scale bar: 2 mm. The response of the antenna implant can be accessed wirelessly, as revealed by the presence of a peak in the scattered signal at the resonant frequency of the antenna. (d) This antenna is sufficiently compact to be implanted in an elastomeric gelatin matrix using standard medical syringes with an inner diameter of 350 μm, hence helping to minimize discomfort during and after implantation. Scale bar: 2.5 mm. By tuning the geometrical parameters of the two-dimensional layout (e), helical antennas of different geometries can be achieved (f). The spatial distribution of the intensity of the emanated magnetic field outside the antenna is presented for the case of (g) a small and (h) larger opening angle α. Optimization of the antenna performance was performed by monitoring the effect of the relevant geometrical parameters, i.e., the stripe length (i), diameter (j) and opening angle (k), on the return loss of the antenna -the S11 parameter.
There are several issues to consider while designing an in-body implant, for example, its power consumption, biocompatibility and the total size of the system. For the latter, typical dimensions of in-body implants are in the centimeter range.5, 6, 10 Hence, surgical treatment is unavoidable to implant the device. However, if the length of the device is ~5 mm and the diameter is <0.5 mm, the device can be readily implanted using standard medical syringes, greatly minimizing discomfort during and after an implantation.
Electronic components to acquire and process data from numerous sensors, including pH and temperature monitoring, are appropriately small already; dimensions as small as 0.3 × 0.3 × 0.15 mm3 (width × length × thickness) are industry standards for high-performance electronics. The main challenge to realize in-body implants is miniaturization of the antenna. For the realization of in vivo smart implants, the antenna should operate in the industry-scientific-medical (ISM) radio band. ISM frequencies of 2.4 GHz or even 5.8 GHz are typically chosen for in-body implants as a compromise between small antenna size (higher frequencies are beneficial) and acceptable penetration through human body tissues (lower frequencies are beneficial).14, 15, 16 A standard dipole antenna operating at 5.8 GHz would have a nominal length of 25.8 mm, which can be reduced by embedding it into a high-k dielectric matrix.17 When integrated on chip, modern antennas, although as small as 2 × 1.5 mm2, require specially designed ground planes and metallization-free regions, which result in a total area occupied by the complete antenna element of at least 4 × 3 mm2,18 (typically, commercial antenna realizations consume a few square centimeters). The increase of the footprint is mainly because of the strict requirements imposed by the need for impedance matching to 50 Ω to ensure good transmitting efficiency.
Aiming for the device miniaturization, it is insightful to wind the standard dipole antenna into a helix, resulting in a normal mode helical antenna.19 This type of antenna is superior in length compared with a dipole antenna operating at the same frequency. Indeed, a tightly wound helix with a diameter of ~200 μm is only 5.5 mm in length, five times shorter than the corresponding dipole antenna. A helical antenna can be prepared manually by winding a wire around a cylindrically shaped dielectric support.20 However, keeping in mind the commercialization of the technology, manual fabrication of small-sized helixes is economically questionable. Therefore, advanced fabrication technologies, for example, conformal printing,21 microcontact printing22, 23 and rolled-up strain engineering,24, 25, 26, 27, 28 were suggested and applied to realize metallic and semiconducting helixes with linear dimensions in the tens of micrometer range. However, simple, precise, large-scale and high-yield fabrication of high-performance helical antennas that are compact but remain impedance matched to standard 50 Ω electronics is challenging and has not yet been achieved, thus preventing the commercial realization of smart implants. For instance, the necessity of impedance matching does not allow to use microantennas, which are realized by printing technologies22, 23, 29 or folding30 without the use of additional matching components. The use of impedance matching elements increases the footprint, price and number of technological steps per antenna fabrication sequence.
Here, we applied strain engineering31, 32 in polymeric-metal heterostructures33, 34 to fabricate arrays of compact normal mode helical antennas operating at the ISM frequencies of 5.8 and 2.4 GHz using a single-step self-assembly process. After optimization, the total length of the three-dimensional (3D) antenna was only 5.5 mm, approximately five times smaller than that of the conventional two-dimensional (2D) realization of a dipole antenna. Independent of its compactness, the helical antenna still remains matched to the impedance of the transmitter of 50 Ω and does not require additional matching components. The possibility to match the impedance of the compact antenna is the unique feature of the Swiss roll geometry of our helical antenna, where the diameter, number of windings of the helix and separation between windings can be tuned by adjusting the conditions of self-assembling the initially planar antenna layout (Figure 1e) into a tightly wound tubular architecture (Figures 1f and 2a). In this work, an inner diameter of the helical antenna of ~200 μm is selected, which is motivated by geometrical considerations to integrate the antenna wire with a length of several tens of mm and a width of 100 μm into a tubular architecture with a length of 5.5 mm. Structures with these geometrical parameters are easily implantable with the standard medical syringes35 using 16–26 gauge needles with typical inner diameters of 1.19–0.26 mm. For demonstration purposes, we implanted the helical antenna into an elastomeric gelatin matrix using standard medical syringes with an inner diameter of 350 μm (Figure 1d). We successfully demonstrate the transmission and receiving signals between two helical antennas as well as the efficient communication between an antenna and a smartphone. Furthermore, because of its tubular shape and appropriate dimensions, the helical antenna fits naturally into the limited space available, for example, in dental implants (Figures 1a–c). To this end, we demonstrate that the antenna can be embedded in a tooth model (Figure 1c), thus demonstrating its potential implant applicability.
Experimental realization of the helical antenna. Relying on the strain engineering platform schematized in (a), helical antennas with and without encapsulation can be realized (b). By tailoring the differential stain of the polymeric strained bilayer, antennas of different diameters are achieved (c). By varying the 2D layout before the self-assembly process into a tubular architecture, different geometries of individual antennas (c, d), as well as antenna arrays (e), can be fabricated. Experimentally measured return loss -the S11 parameter- for two antennas with different diameters (f).
Materials and methods
Treatment of the substrate
Cover glasses with dimensions of 22 × 22 mm2 and a thickness of 150 μm (Menzel cover glasses, Gerhard Menzel GmbH, Braunschweig, Germany) were used. First, the substrates were sonicated for 5 min by immersing them in acetone and isopropanol, followed by subsequent rinsing in deionized (DI) water. Then, the substrates were sonicated for 30 min in a 2% water solution of Alconox cleaner (Alconox, Inc., White Plains, NY, USA) and rinsed thoroughly using DI water under ultrasonic conditions. After cleaning, the substrates were kept in DI water to prevent them from contamination and to keep the surface hydrolyzed.
Adhesion layer
For better adhesion of the polymeric layers, the substrates were modified with self-assembled monolayers of 3-(trimethoxysilyl) propyl methacrylate (Polysciences Europe GmbH, Eppelheim, Germany), which is performed in toluene (Sigma-Aldrich LLC, Sigma-Aldrich Chemie GmbH, Munich, Germany) 1.5% (v/v) mixture of silane for 20 min. Afterward, the substrates were washed in toluene, dried using nitrogen gas and baked on a hotplate at 120 °C for 5 min under a nitrogen atmosphere.
Sacrificial layer
The polymeric sacrificial layer was fabricated in a manner as described elsewhere.36 The sacrificial layer solution was spin coated at 3000 r.p.m. for 35 s to produce a 500-nm thick layer. Drying was performed at 60 °C for 5 min, and rapid dipping of the sample was performed in 2 M CaCl2 solution. Patterning of the sacrificial layer was performed using conventional MAP1210 photoresist during the development process of the photoresist in alkali developer. The photoresist was removed using (1-methoxy-2-propyl) acetate (Sigma-Aldrich LLC). Finally, the samples were annealed at 200 °C for 5 min under a nitrogen atmosphere.
Strained bilayers
The differential strain in the polymeric bilayer was introduced by swelling one of the polymers in an aqueous media while the other layer was kept in a nonswollen state.
The solution for the swelling layer was prepared by the reaction of N-(2-hydroxyethyl)acrylamide and poly(ethylene-alt-maleic anhydride) in N,N-dimethylacetamide (DMAc) and photosensitized using 2% (wt/wt) 2-benzyl-2-(dimethylamino)-4-morpholinobutyrophenone (Sigma-Aldrich LLC). Here, 6 g of poly(ethylene-alt-maleic anhydride) was dissolved in 50 ml of DMAc, and 2 g of N-(2-hydroxyethyl)acrylamide was added. The reaction was performed for 10 h at room temperature. The solution was spin coated at 4000–8000 r.p.m. for 35 s, resulting in layer thicknesses of 300–150 nm, respectively. After drying the polymeric layer at 50 °C for 5 min, the sample was exposed to a 405-nm mercury h-line (20 mW cm2) for 1.5 min through a glass/Cr mask in a SUSS MA4 mask aligner (Karl Suss KG - Gmbh & Co, Munchen-Garching, Germany). Development was performed in DMAc for 30 s, followed by subsequent rinsing in isopropanol. Finally, the sample was annealed at 200 °C for 5 min under a nitrogen atmosphere.
We used polyimide as the nonswelling layer. Photosensitive polyimide was synthesized by the reaction of 3,3',4,4'-biphenyltetracarboxylic dianhydride and 3,3'-diaminodiphenylsulfone in DMAc, modified with dimethylaminoethyl methacrylate and photosensitized using 2% (wt/wt) 2-benzyl-2-(dimethylamino)-4-morpholinobutyrophenone (Sigma-Aldrich LLC). The polymer synthesis was performed by dissolution of 9.93 g of 3,3'-diaminodiphenylsulfone in 20 ml of DMAc with the subsequent addition of 12.8 g of 3,3',4,4'-biphenyltetracarboxylic dianhydride. After mixing for 12 h at 70 °C, the solution of polyamic acid in DMAc was obtained. The solution was modified by reaction with 12.5 g of dimethylaminoethyl methacrylate. The polymer was spin coated at 2000–8000 r.p.m. for 35 s, resulting in layer thicknesses of 1700–500 nm, respectively. After drying the polymeric layer at 50 °C for 10 min, the sample was exposed to a 405-nm mercury h-line (20 mW cm2) for 1.5 min through a glass/Cr mask in a SUSS MA4 mask aligner. Specially, the adjusted shape of the edges of the nonswelling layer predetermines the rolling direction by preventing the rolling of the structure from the sides (Supplementary Figure 8).
Development was performed in 1-ethyl-2-pyrrolidone for 1 min, followed by subsequent rinsing in isopropanol. The imidization process of the achieved structures was performed on a hotplate at 250 °C for 10 min under a nitrogen atmosphere.
Metal antenna layer
Patterning of the antenna layer was performed using the lift-off process with AR-P3510 (ALLRESIST GmbH, Strausberg, Germany) photoresist. First, we spin-coated the photoresist at 3000 r.p.m. for 35 s and dried it on a hot plate at 90 °C for 4 min. Then, the sample was exposed to a 405-nm mercury h-line (20 mW cm2) for 12 s through a glass/Cr mask in a SUSS MA4 mask aligner. Development was performed in the diluted developer (AR300-35, ALLRESIST GmbH, Strausberg, Germany) with DI water in the proportion of 1:1 (v/v) for 20 s, followed by subsequent rinsing in DI water and drying in nitrogen flow.
The metal layer stack consisting of Ta(10 nm)/Cu(100 nm)/Ta(10 nm) was prepared by magnetron sputtering at room temperature (Ar was used as the sputtering gas at a partial pressure of 10−3 mbar; the base pressure in the chamber was <10−7 mbar). To improve the stability of the electrical contact, an additional layer of Au (20 nm) was deposited using thermal evaporation. The lift-off process of the metal stack was performed by swelling the photoresist in acetone and further rinsing in isopropanol.
The 2D layouts were rolled-up into 3D helical antennas by selectively etching the sacrificial layer in a strong chelating agent solution of 0.5-M sodium EDTA (VWR International GmbH, Darmstadt, Germany). After the etching process, the rolled-up antennas were washed in the DI water solution with isopropanol in the proportion of 5:1 and dried at ambient conditions.
Characterization of the antenna
The S11 and S12 parameters of the rolled-up antennas were measured using the CASCADE PM-8 (Cascade Microtech GmbH, Thiendorf, Germany) probe station and Agilent E5071 (Agilent Technologies Sales & Services GmbH & Co.KG, Waldbronn, Germany) vector network analyzer in the 300 kHz–20 GHz frequency range. All the electric contacts to the antennas were made using GSG CASCADE Z-probes. To eliminate the coupling effect due to the reactive near field of the antenna and the metallic chuck of the probe station, all the experiments were performed on a 20-mm thick teflon block.
Antenna encapsulation and fabrication of the frame
The solution to prepare the frame was composed of acrylic acid (AA), triethylamine and polyacrylic acid MW=450 000 (Sigma-Aldrich LLC). First, we diluted 0.1 g of polyacrylic acid in 10 g of AA and added 14.18 g of triethylamine dropwise during the stirring process until the product stopped fuming. Then, this pre-polymer was diluted by an additional 30 g of AA and photosensitized by 5% (wt/wt) 1-hydroxycyclohexyl phenyl ketone (Alfa Aesar, Alfa Aesar GmbH & Co KG, Karlsruhe, Germany). The frame was formed by exposing the solution at 376 nm using a direct laser writer (8 mW-UV laser from Coherent GmbH, Coherent LaserSystems GmbH & Co. KG, Hannover, Germany) installed in a 3-axial robot (Fisnar F7300N, Fisnar Europe Glasgow, UK). The scanning speed for the curing process of the polymer material was set to 1 mm s−1. The sample was then washed in acetone, resulting in the frame around the antenna. This frame was then filled with the encapsulation solution. Dissolution of the frame was performed in an ammonia solution (pH 12) for 10 min with subsequent rinsing in DI water.
Encapsulation solution
The UV-curable encapsulation solution was prepared by mixing 1,6-hexandiol diacrylate, bisphenol A-glycerolate (1 glycerol/phenol) diacrylate and poly(ethylene glycol) diacrylate MW=250 and 700 (Sigma-Aldrich LLC). All the components were thoroughly mixed in the following proportion: 6 g of 1,6-hexandiol diacrylate, 9 g of bisphenol A-glycerolate (1 glycerol/phenol) diacrylate, 9 g of poly(ethylene glycol) diacrylate (MW=250), 4.5 g of poly(ethylene glycol) diacrylate (MW=700) and 2% (wt/wt) 2-benzyl-2-(dimethylamino)-4-morpholinobutyrophenone (Sigma-Aldrich LLC.).
To increase the dielectric constant of the polymer, we added 0.5 g BaTiO3 (Sigma-Aldrich LLC) in 2 g of the prepared solution. Before mixing, the BaTiO3 was silanated to enhance the bonding strength between the inorganic filler and organic binder. For silanation, the BaTiO3 was sonicated with 1% (wt/wt) 3-(trimethoxysilyl)propyl methacrylate (Polysciences Europe GmbH) in acetone for 1 h. The solution was then left in a Petri dish for 30 min to evaporate the silane and acetone, followed by dehydration at 120 °C on a hot plate. After filling the internal area of the frame, the encapsulation solution was exposed for 20 s using a lamp with a wavelength of 450 nm (100 W; 150 mW cm2 at a 10-cm distance).
Permittivity of the encapsulating polymer
The encapsulation solution was applied between two teflon sheets and exposed for 20 s to a lamp with a wavelength of 450 nm (100 W; 150 mW cm2 at a 10-cm distance). The cross-linked polymeric foil was peeled from the teflon surface and cut into 10 disks with 10-mm diameters. The thickness of the disks was 180 μm, as measured by a micrometer screw gauge (averaged over 10 samples). Each disk was placed between polished aluminum cylinders of the same diameter, forming a capacitor. Capacitance measurements were performed at frequencies ranging from 100 Hz to 100 MHz using an Agilent 4294H impedance analyzer, resulting in a capacitance of 30 pF (averaged over 10 samples). The calculation of the permittivity based on the standard capacitance equation accounting for the geometry of the capacitor enabled us to determine the permittivity of the encapsulating polymer, which was 3.88.
Simulation parameters of the human head model

Gain of the antenna and communication distance
Miniaturization of the, for example, dipolar antenna or normal mode helical antenna unavoidably leads to a decrease in the gain of the antenna even if it remains impedance matched. If the maximum distance between the antenna and the receiver and the output power of the antenna are fixed, miniaturization of the antenna is possible up to the point when the incoming power at the receiver exceeds its noise floor. The required gain of the antenna can be estimated as follows:

Our normal mode helical antenna possesses a gain of −46 dBi (Figure 5d), including the gain and directivity of the antenna, which clearly demonstrate that it can be used to efficiently communicate at distances of up to 2 m. For this operation, the corresponding S12 parameter should be better than −96 dB.
Results and Discussion
Self-assembled Swiss roll geometries have been applied to a wide range of rolled-up devices (for example,37, 38, 39, 40, 41, 42) based on semiconductor, oxide and metal strained layer engineering. However, for antenna applications, metal-based strained layers are not appropriate because of signal screening. Semiconductor- and oxide-based platforms are too brittle to successfully roll-up the initial planar strained layers into a tube with the desired dimensions of ~200 μm in diameter and 5 mm in length. Furthermore, to improve the mechanical performance of the helical antenna and allow for adjustment of its electrical properties, for example, resonance frequency; the encapsulation of the antenna by polymeric materials is highly beneficial, although not supported by the aforementioned platforms. Based on this consideration, the polymeric-based approach appears to be the most suitable. Techniques relying on differentially strained photopatternable SU8 in combination with metal patterning have already been introduced.43 To produce arrays of normal mode helical antennas over large areas with high yield and allow for their encapsulation, we developed a strain engineering platform relying on photopatternable, thermally and chemically stable imide- and acrylic-based polymers. Furthermore, we precisely define the combination of different processing steps and the material combinations in exactly the right order, allowing us to achieve high-yield production of compact normal mode helical antennas over large areas in a cost- and time-efficient self-assembly process.
Optimizing the performance of normal mode helical antennas via modeling
Before the experimental realization of the helical antenna, we performed a series of finite element simulations to determine the relevant range of geometrical parameters to achieve the resonance frequency of the normal mode helical antenna at 5.8 GHz after encapsulation in a polymeric matrix with dimensions smaller than the wavelength in this material. To optimize the performance, we considered the 2D layout shown in Figure 1e, which is transformed into a Swiss roll-shaped tubular architecture with multiply windings (Figure 1f). The antenna consists of a 2-μm thick and 100-μm wide conducting wire. The vertical separation between the windings is fixed to 2 μm, which is the typical thickness of the polymeric layers. The structure is prepared on a 150-μm thick glass substrate. All the geometrical parameters in the simulation are identical to those in the experiment except the thickness of the wire, which is only 100 nm in the experiment. To account for the different thicknesses, the conductivity of the simulated 2-μm thick metal layer was scaled down to match the conductivity of the experimental 100-nm thick Au wire. With this adjustment, the total conductance of the antenna wire remains the same; hence, this approach, although artificial, allows the complete physical picture of the transmission properties of the antenna to be correctly captured (Supplementary Figure 1).
In the following text, we describe the impact of the relevant geometrical parameters (Figures 1e and f), namely, the inner diameter Ø, the angle α and the stripe length L, on the return loss of the antenna—the S11 parameter. The latter determines the efficiency of the antenna in transmitting the data to an external device and is typically expressed in dB (log scale). Transmitting devices with S11>−10 dB are classified as antennas.44 When the stripe length L, the spacing between windings and the final length of the helical antenna are fixed, the number of windings in the Swiss roll architecture N, is only dependent on the inner diameter of the tube. For the 5.5-mm long antenna with L=15.5 mm and an interwinding spacing of 2 μm, the number of windings in the helix varies from 45 to 11 when the diameter is changed from 20 to 400 μm (Supplementary Figure 2).
When the operation frequency, f, and the inner diameter, Ø, of the antenna are fixed, the optimization of the final length of the antenna requires a parametric investigation of the effect of the angle α and the stripe length L on the S11 parameter (Figure 1i). The target antenna length is represented by the curve in the parameter space (L, α). The region below this curve corresponds to the antenna length being smaller than the target length. The optimization procedure is successful whenever there are antennas in this region with S11 parameters better than −10 dB. A typical example for antennas without encapsulation with Ø=160 μm and resonant frequency f=7.2 GHz is shown in Figure 1i. The shaded region indicates the parameter space, where the target length of the helical antenna is smaller than 5.5 mm. In the region of interest, there is a set of geometrical parameters of the 2D layout, 15 mm<L<16 mm and 8°<α<11°, which satisfies the resonance condition with S11>−10 dB. Based on this study, we use a stripe length of L=15.5 mm for further investigations. The resonance frequency of 7.2 GHz in free space is selected because after encapsulation of the antenna in a polymeric matrix with a permittivity of ~4, the resonance frequency can be decreased to the desired value of ~5.8 GHz (Figure 3a).
Encapsulation of the antenna. The simulated return loss of the antenna—the S11 parameter—as a function of the frequency and the permittivity, ɛ, of the encapsulating material is shown in (a). The S11 parameter of two experimentally realized antennas of different diameters is measured as a function of frequency before and after the encapsulation process (b). Encapsulation results in a reduction of the resonance frequency of the antenna. The inset in (b) shows the optical micrographs of the antenna with a 100-μm diameter before and after encapsulation.
Interestingly, a change in the inner diameter, Ø, only moderately affects the performance of the helical antenna (Figure 1j). The antenna exhibits two resonant peaks in the frequency range up to 20 GHz. The main peak is positioned at ~7 GHz, and a second peak is observed at higher frequencies. Both resonant peaks reveal shifts toward larger frequencies when the diameter decreases. The shift of the main peak is rather small, which can be understood as follows: antennas of smaller diameter exhibit lower inductance. However, as the simulations are performed for the constant stripe length L, lowering of the diameter is accompanied by an increase in the number of windings in the structure (Supplementary Figure 2). These two effects lead to only a moderate decrease of the inductance for smaller diameters of the structure, which is reflected only in the slight change of the resonant peak position (Figure 1j). Furthermore, we observe a reduction in the efficiency of the antenna with smaller diameter, which is mainly due to the onset of electromagnetic interaction between the wires in neighboring windings when the period of the helix becomes comparable to the width of the wire. As will be discussed further, in this case, the strength of the emanated magnetic field outside the antenna is lowered, resulting in a reduced emission of the signal.
A 2D plot summarizing the return loss of helical antennas as a function of frequency f and angle α is shown in Figure 1k. The other two geometrical parameters are kept constant at L=15.5 mm and Ø=160 μm. For α>8°, the antenna exhibits two resonant peaks. The positions of the two peaks are dependent on the angle α with a tendency to shift toward the lower frequency range with an increasing angle. Remarkably, a return loss of the antenna of up to −15 dB is achieved for 10°<α<30°, indicating that the helical antenna can efficiently emit the signal. Interestingly, for α<8°, there are no resonant peaks observed (Figure 1k). At small angles, the self-assembly process results in the formation of rather short antennas with laterally overlapping wires between neighboring windings (the pitch of the helix is smaller than the wire width). For the limiting case, α=0, two coils are formed instead of helices (Supplementary Figure 3). Accounting for the opposite direction of propagating currents in both helices, the emanating magnetic fields will compensate each other. In this case, the mutual inductance will cancel the self-inductance, and the antenna will act as a capacitor without transmitting the signal. The strength of the magnetic field outside the antenna is shown in Figures 1g and h for α=2.5° and 10°, respectively. The comparison reveals that a strong magnetic field (Figure 1h) and good antenna performance (Figure 1k) can be achieved when the period of the helix is larger than the wire width.
The performed simulations indicate that the optimal performance with S11 ~−15 dB is expected for a normal mode helical antenna with a total length of 5.5 mm when the 2D layout is formed with α=10° and L=15.5 mm. The realized helical antenna with an inner diameter of ~160 μm possesses a resonant frequency of ~7.2 GHz in free space (Figure 1f, antenna #2).
The mechanical and electrical properties of these antennas can be improved by encapsulating them in a polymeric matrix with a defined dielectric constant. The return loss of the antenna, the S11 parameter, for the chosen set of geometrical parameters as a function of the frequency and permittivity, ɛ, of the encapsulating material is shown in Figure 3a. In this simulation, the polymeric matrix possesses dimensions that are smaller than the wavelength in this material. When the antenna in free space operates in resonance at 7.2 GHz, the encapsulation results in the monotonous decrease of the resonant frequency with a clear trend toward saturation at 5.6 GHz, which is already achieved for ɛ=6. A further increase of the permittivity of the encapsulating material does not affect the location of the main resonant peak. These results are used as an input for the experimental realization of the antenna (Figure 2).
Experimental realization of compact normal mode helical antenna
Figure 2a summarizes the fabrication steps of the normal mode helical antennas. On the adhesion promoted glass substrate (Methods #1 and 2), we spin coat and photopattern each layer of the functional stack, consisting of a sacrificial layer and a strained bilayer. Here, we apply an acrylic-acid-based sacrificial layer36, which offers numerous advantages for further processing, using conventional thin-film and photolithography techniques: this sacrificial layer is stable at high temperatures up to 650 °C, inert in common organic nonpolar, polar protic and aprotic solvents, as well as in moderate bases and acids, and photopatternable using standard 365–405 nm exposure sources. The strained bilayer consists of a hydrogel layer expandable in neutral aqueous or alkaline solutions and the polyimide layer, which is chemically and thermally inert and mechanically rigid. Each layer is prepared, exposed and developed as described in Methods #3 and 4. This advanced layer stack also allows for multiple lithography steps on the metal layers, as required in microelectronics processing.
Onto the functional polymeric layer stack, we deposit conductive wires consisting of a Cr(5 nm)/Au(100 nm) bilayer using a lift-off photoresist mask (Methods #5). The formed planar 2D layouts are self-assembled into 3D helical antennas by selectively etching the sacrificial layer in a strong chelating agent solution of 0.5 M sodium EDTA. After the etching process, the helical antennas are washed in DI water solution with isopropanol in a 5:1 ratio and dried at ambient conditions. One of the benefits offered by the developed technology is that tubular architectures can be wet processed and directly withdrawn from the solution (Supplementary Movie 1), as they are mechanically stable even without the use of super-critical drying.
By tuning the thickness of the polymeric layers in the strained stack, 5.5-mm long Swiss rolls of different diameters ranging from 100 to 350 μm with 12–30 windings are achieved (Figure 2c). By varying the 2D layout, different geometries of the helical antennas can be readily realized (compare Figure 2c and d). Furthermore, single antennas, as well as arrays of antennas, can be prepared (Figure 2e). As the array can be achieved in a single self-assembly process, these 2D arrays of helical antennas could be advantageous in producing metamaterials for the microwave region in the spirit of recent work by Slobozhanyuk et al.45
To access the performance of the antennas, we employed an Agilent vector network analyzer with GSG probes in the frequency range of 300 kHz–20 GHz (Methods #6). Figure 2f shows the frequency dependence of the return loss of the antenna for the two antennas with diameters of 100 and 160 μm. Close to the theoretical prediction, the main resonance of the antennas is located at ~8 GHz, and the antenna of smaller diameter possesses a slightly higher resonant frequency (compare Figures 2f and 1j).
The possibility to realize arrays of compact self-assembled antenna elements addresses the long-standing practical problem that prevents the commercial realization of smart implants. In this respect, we demonstrate that arrays of antennas can be produced over large areas in a single-step self-assembly process, paving the way toward high-volume and cost-efficient fabrication of compact communication devices. Relying on the developed technology, we are able to fabricate rolled-up architectures on glass wafers with areas of 10 × 10 cm2. The tubes homogeneously cover the entire area of the wafer (Supplementary Figure 4). Experiments on larger substrates were not performed, as these substrates could not be processed using the available experimental equipment. However, the proposed fabrication approach imposes no limitations on the processing area to realize arrays of antenna devices. Monitoring the quality of the self-assembly process over 68 antennas enabled us to quantify the fabrication yield as better than 90%. The measurements of the characteristics of 15 antennas arbitrarily chosen from the array are shown in Supplementary Figure 5.
Encapsulation of the normal mode helical antenna
These free-standing antennas were then encapsulated into a polymeric matrix (Figure 2b) to enhance the mechanical stability of the 3D architecture and to shift the resonant frequency of the rolled-up antenna to the lower band (Figure 3b). For encapsulation, the tubular architectures were processed as follows (Supplementary Movie 2). First, we created a dissolvable frame around the antenna (Methods #7). The frame determined the region, which was filled with the encapsulation solution consisting of silanated BaTiO3 mixed with an organic binder (Methods #8). The electrical characterization of the encapsulating polymer revealed its permittivity to be ~3.88 (Methods #9). After curing the encapsulation solution, the frame was removed in an aqueous ammonia solution. As predicted theoretically (Figure 3a), the encapsulated devices possessed resonant peaks at smaller frequencies (Figure 3b). For instance, the resonance frequency of the antenna with a diameter of 350 μm was shifted to 5.7 GHz, which is close to the desired value of 5.8 GHz of the ISM band. It is important to emphasize that even after encapsulation, the antennas revealed an S11 parameter larger than −10 dB, clearly demonstrating their suitability for communication tasks.
Communication between two normal mode helical antennas
The two encapsulated antennas shown in Figure 3b were used to demonstrate the possibility of transmitting and receiving signals using compact normal mode helical antennas. The signal accepted by antenna #2 when emitted by antenna #1 –the S12 parameter- is shown in Figure 4a and b for different separation distances between the antennas. The simulation results, accounting for the exact geometry of the experimental setup, are in good agreement with the measured signal (Figure 4a). The model used for simulations is shown in Supplementary Figure 6.
Data transmission using compact helical antennas. Communication between the two helical antennas shown in Figure 3b separated by 35 mm is shown in (a). The experimental arrangement of the antennas is shown in the inset in (a). An increase of the distance between the antennas results in a decrease of the intensity of the received signal (b). Communication at a distance of 95 mm is still successfully demonstrated. The helical antenna is applied to receive the signal from a smartphone (c) transmitting at 2.4 and 5.65 GHz. The inset in (c) presents a photograph of the experimental setup while establishing communication with the smartphone.
The received signal consists of several peaks. Three of the peaks can be clearly attributed to the resonances of the antennas (~6, ~14, and ~19 GHz). Additionally, there are peaks at frequencies below 5 GHz. These peaks are less pronounced but also present in the simulation data (Figure 4a) and originate from the reflection of the emitted signal from the components of the experimental setup, for example, the probes and microscope. As expected, the increase of the distance between the helical antennas results in a weaker received signal (Figure 4b).
Communication between a normal mode helical antenna and a smartphone
In addition to the communication between two antennas, we demonstrate the possibility of the compact helical antenna to receive data from an external device. For demonstration purposes, we selected a smartphone, which was adjusted to transmit data packages in continuous mode with a 100% duty cycle and a 20-dBm emission power at 2.4 and 5.6 GHz. These signals were successfully received by the encapsulated helical antenna (Figure 4c).
Addressing helical antenna embedded in a tooth model
For this demonstration, we embedded the encapsulated normal mode helical antenna into a tooth model composed of acryl (inset in Figure 1c). As relevant for implant applications, the embedded antenna was located in the far-field region at a distance of 220 mm from the transmitting antenna. For the latter, we used a standard dipole antenna tuned to the resonance frequency of 5.8 GHz. As the helical antenna is not equipped with a transceiver module, we applied the backscattering approach to address it. In this measurement protocol, we monitored the scattered power from the investigated antenna by receiving the reflected signal in phase with the transmitted signal. The measurements were performed using a network analyzer tuned to an output power of −5 dBm, a bandwidth of 10 kHz and an averaging sampling of 36.
First, we performed the reference measurement of the transmitting antenna by investigating the frequency dependence of its return loss, the S11 parameter. In this study, the helical antenna is not inserted in the model of a tooth. In this manner, we captured the possible impact of the complex environment on the scattered signal. Next, we introduced the encapsulated helical antenna into the tooth and monitored the modification of the scattered signal with respect to the reference measurement. The signal after subtracting the reference measurement and averaging over multiple experiments to eliminate the possible effect of the environment is shown in Figure 1c as the frequency dependent antenna response, ΔS11. The presence of a clear peak in the scattered signal at the resonant frequency of the helical antenna unambiguously proves the possibility of radiating a signal sufficiently strong to be detected by the end device.
Targeting in vivo implant applications
When targeting, for example, tooth implant applications, the antenna should be located in a human body, where teeth, as well as surrounding biological tissues, will affect the characteristics of the antenna compared to those in air. To address this important aspect, we performed extensive simulations of the performance of the antenna for relevant cases such as a tooth implant and the presence of an antenna under the skin.
For these simulations, we constructed a model of a human head (Figure 5a) including teeth, bones, tongue, brain, and skin, with relevant physical properties assigned to each component of the model (Methods #10). We started with a normal mode helical antenna with an inner diameter of 350 μm encapsulated in a polymeric matrix and achieved a resonant frequency of 5.8 GHz (Figure 5b). When this antenna was embedded into a bulky dielectric, for example, a tooth, and surrounded by lossy biological tissues with high permittivity, its resonant frequency was reduced to 2.45 GHz (Figure 5b). This lowering of the operation frequency of the antenna to 2.45 GHz conveys strong advantages, namely, (i) the 2.45 GHz frequency also belongs to the ISM radio band and is hence appropriate for implant applications and (ii) the absorption of electromagnetic waves in a human body is substantially reduced at 2.45 GHz compared with 5.8 GHz; thus, a lower transmitter power can be potentially used. Furthermore, when targeting the operation frequency of 5.8 GHz in the human body, the length of the normal mode helical antenna can be reduced even further from 5.5 mm to ~2.5 mm.
Targeting in vivo applications. The human head model used for the simulations is shown in (a). The inset shows a close up of the helical antenna embedded into a tooth. (b) The frequency dependence of the S11 parameter for the helical antenna (diameter: 350 μm; encapsulated in a polymeric matrix) used as a tooth implant or implanted under the skin. The resonant frequency is shifted down to 2.45 GHz for the tooth implant. (c) The spatial distribution of the electric field of the antenna. (d) The radiation pattern of the antenna (gain of the antenna is plotted). The calculation was performed at 2.45 GHz. (e) Attenuation of the signal transmitted by the antenna to the receiver as a function of the distance between transmitter and receiver. The antenna can communicate up to a distance of 2 m in air. A dipole antenna is used as a receiver. (f) Orthogonal cuts through the center of the helical antenna, revealing the spatial distribution of the specific absorption ratio calculated with respect to 10 g of body tissue. The transmitting power of the helical antenna is 25 μW. The calculation was performed at 2.45 GHz.
The spatial distribution of the electric field of the antenna is shown in Figure 5c. These data can be replotted as a radiation pattern (Figure 5d), indicating that the antenna radiates efficiently outside the body in the direction of the receiver with a gain of −46 dB. In contrast, the gain of the antenna in the direction into the body is approximately −65 dB only, indicating strong attenuation of the signal, most likely due to absorption while the electromagnetic wave is travelling in the inhomogeneous lossy biological media of bones, skin and so on. The general trend of the signal attenuation with the increase of the distance between the helical antenna (transmitter) and dipolar antenna (receiver) is presented in Figure 5e. Relying on the antenna gain and accounting for the typical receiver sensitivity of −110 dBm standard for mobile applications, we estimate that the implanted helical antenna can be used for communication up to a distance of 2 m (see Methods #11). With this performance, the realized normal mode helical antenna with a footprint of <5.5 × 0.5 mm2 is suitable for short-range communication, as needed for smart implant applications, for example, communication with a smartphone (Figures 1a and 4c). The achieved short-range operation represents the classical trade-off between the miniaturization of the antenna and its transmitting potential. For instance, a folded antenna with a six times larger footprint of 17.7 × 1 mm2 can be used for communication at a distance of up to 20 m20.
As the helical antenna is designed for wireless implantable systems, it is imperative to consider the specific absorption ratio (SAR) for electromagnetic waves propagating in lossy biological tissues. SAR studies are performed for the antenna used as a tooth implant (Figure 5f). For these simulations, we assumed a transmitter power of the antenna of 25 μW20. The simulations show that the SAR calculated with respect to 10 g of body tissue does not exceed 2 mW kg−1, which is well within the limits of 2 W kg−1 imposed by the IEEE Standard for Safety Levels with Respect to Human Exposure to Radio Frequency Electromagnetic Fields.
The local environment around the antenna affects its radiation characteristics. We performed a series of simulations with the antenna implant located under the skin and between the skin and a skull. Here, the standard three-layer model of a head was used. The discussion above remains qualitatively valid; however, there are quantitative differences observed, including a shift of the working frequency of the antenna even further to ~2.2 GHz, which is due to the higher permittivity of the skin and is also accompanied by an improvement of the S11 parameter (Figure 5b).
Conclusion
In conclusion, we fabricated compact normal mode helical antennas operating in the ISM radio band at 5.8 GHz. After optimization, a total length of the 3D antenna of only 5.5 mm was achieved, approximately 5 times smaller than that of the conventional 2D realization of a dipole antenna. We successfully overcame the main hurdles in the implementation of compact antennas, namely, (i) the difficulty of the impedance matching process, allowing us to directly use the helical antenna without the need for introducing external matching components to maintain good transmitting efficiency; (ii) mechanical stabilization of 3D helical architectures; and (iii) the need for high-volume and cost- and time-efficient fabrication of the antennas. We have developed a technology platform based on strain engineering relying on photopatternable, thermally and chemically stable imide- and acrylic-based polymers, which allows us to encapsulate the antenna with polymers, providing another important knob to tune the resonance frequency. Relying on the developed technology, we were able to produce arrays of antennas over large areas with a greater than 90% yield in a highly parallel self-assembly process, which may potentially enable low-cost production of compact communication devices. The commercialization potential is facilitated by the use of industry standard processing equipment, including optical lithography and electron beam evaporation devices.
The realized normal mode helical antenna is designed to be impedance matched to 50 Ω without relying on any external active or passive components. Therefore, the total footprint of the antenna of less than 5.5 × 0.5 mm2 corresponds to the size of the complete antenna element. With these geometrical parameters, this device is the smallest reported antenna that works at 5.8 GHz and is impedance matched to 50 Ω, which is the most common impedance for microelectronic devices. To address the issue of compatibility with higher ohmic devices, we simulated the performance of the antenna when impedance matched to 50, 75, 90 and 125 Ω (Supplementary Figure 7). Interestingly, without changes to the dimensions or geometry, the antenna appears to be matched to all these standard impedances, as it exhibits an S11 parameter better than −10 dB at resonant frequency. This possibility of being matched to these most standard impedances is of great advantage, as the same antenna can be used with different electronics without adjustments.
We experimentally demonstrated efficient communication between antennas at distances of up to 95 mm. Furthermore, the communication between a helical antenna and a smartphone was successfully realized. Because of the shape and dimensions, the fabricated antennas are readily implantable using standard medical syringes. In addition, we accessed the response of an antenna embedded in a tooth model. These demonstrations highlight the potential of helical antennas for medical applications as components of smart system implants. This was verified by modeling the antenna performance and SAR for electromagnetic waves when the antenna was embedded in the model of a human head, correctly accounting for relevant biological tissues. When embedded in the model of the human head, the working frequency of the antenna was reduced to 2.45 GHz, resulting in the smallest antenna operating at the 2.45 GHz ISM band while still being impedance matched to standard electronics.
Experimental realization of the functional smart implant requires further development steps, where the compact antenna will be integrated as part of a functional element of radio-frequency identification systems and combined with various data acquisition devices, for example, pH and temperature sensorics, to enable realization of fully functional wireless in-body implants. In addition, the proposed technology can be extended, and the helical antenna can be prepared in a single fabrication process out of the planar layout, accommodating various functional elements, including energy storage,46, 47 active electronics,39 and magnetic48 and fluidic41 sensorics, hence realizing in vivo smart implants based on multifunctional compact electronics.49
References
Cao, H., Rao, S., Tang, S. J., Tibbals, H. F., Spechler, S. & Chiao, J. C Batteryless implantable dual-sensor capsule for esophageal reflux monitoring. Gastrointest. Endosc. 77, 649–653 (2013).
Young, D. J . Development of wireless batteryless implantable blood pressure-EKG-core body temperature sensing microsystem for genetically engineered mice real time monitoring. IEEE Int. Conf. Nano/Molecular Medicine and Engineering (NANOMED) 259–264 (2009).
Mannoor, M. S., Tao, H., Clayton, J. D., Sengupta, A., Kaplan, D. L., Naik, R. R., Verma, N., Omenetto, F. G. & McAlpine, M. C Graphene-based wireless bacteria detection on tooth enamel. Nat. Commun 3, 763 (2012).
Farra, R., Sheppard, N. F. Jr, McCabe, L., Neer, R. M., Anderson, J. M., Santini, J. T. Jr, Cima, M. J. & Langer, R. First-in-human testing of a wirelessly controlled drug delivery microchip. Sci. Transl. Med. 4, 122ra21 (2012).
Wilson, B. S. & Dorman, M. F. Cochlear implants: current designs and future possibilities. J. Rehabil. Res. Dev. 45, 695–730 (2008).
Hodgins, D., Bertsch, A., Post, N., Frischholz, M., Volckaerts, B., Spensley, J., Wasikiewicz, J. M., Higgins, H., Stetten, F. & Kenney, L. Healthy aims: developing new medical implants and diagnostic equipment. Pervasive Comput 7, 14–21 (2008).
Chen, G., Ghaed, H., Haque, R., Wieckowski, M., Yejoong, K., Gyouho, K., Fick, D., Daeyeon, K., Mingoo, S., Wise, K., Blaauw, D. & Sylvester, D . A cubic-millimeter energy-autonomous wireless intraocular pressure monitor. IEEE Int. Solid-State Circuits Conf. Digest of Technical Papers (ISSCC) 310–312 (2011).
Rogers, J. A., Someya, T. & Huang, Y. Materials and mechanics for stretchable electronics. Science 327, 1603–1607 (2010).
Rizzo, J., Shire, D. B., Kelly, S. K., Troyk, P., Gingerich, M., McKee, B., Priplata, A., Chen, J., Drohan, W., Doyle, P., Mendoza, O., Theogarajan, L., Cogan, S. & Wyatt, J. L. Development of the Boston retinal prosthesis. Conf. Proc. IEEE Eng. Med. Biol. Soc 2011, 3135–3142 (2011).
Li, Y., Alam, M., Guo, S., Ting, K. & He, J. Electronic bypass of spinal lesions: activation of lower motor neurons directly driven by cortical neural signals. J. Neuroeng. Rehabil. 11, 107 (2014).
Borton, D. A., Yin, M., Aceros, J. & Nurmikko, A. An implantable wireless neural interface for recording cortical circuit dynamics in moving primates. J. Neural Eng. 10, 026010 (2013).
Hochberg, L. R., Bacher, D., Jarosiewicz, B., Masse, N. Y., Simeral, J. D., Vogel, J., Haddadin, S., Liu, J., Cash, S. S., van der Smagt, P. & Donoghue, J. P. Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature 485, 372–375 (2012).
Lebedev, M. A. & Nicolelis, M. A. Brain–machine interfaces: past, present and future. Trends Neurosci. 29, 536–546 (2006).
Bazaka, K. & Jacob, M. V. Implantable devices: issues and challenges. Electronics 2, 1–34 (2013).
Kumar, V., Sharma, A., Kumar, A., Ahmad, M. & Gupta, G. Interaction of mobile phone waves with tissues of skeletal muscles and bone of human beings. J. Pharm. Biol. Sci 1, 2278–3008 (2012).
Swerdlow, A. J. Health Effects from Radiofrequency Electromagnetic Fields, Health Protection Agency, (2012).
Skrivervik, A., Zurcher, J.-F., Staub, O. & Mosig, J. PCS antenna design: the challenge of miniaturization. IEEE Antennas Propag. Mag. 43, 12–27 (2001).
Balanis, C. A . in Modern Antenna Handbook 1203–1204 (John Wiley & Sons, 2011).
Kraus, J. D. Antennas, (McGraw-Hill, Inc., 1988).
Mizuno, H., Takahashi, M., Saito, K., Haga, N. & Ito, K . Design of a helical folded dipole antenna for biomedical implants in Proc. 5th European Conf. Antennas and Propagation (EUCAP) 3484–3487, IEEE, (2011).
Adams, J. J., Duoss, E. B., Malkowski, T. F., Motala, M. J., Ahn, B. Y., Nuzzo, R. G., Bernhard, J. T. & Lewis, J. A. Conformal printing of electrically small antennas on three-dimensional surfaces. Adv. Mater. 23, 1335–1340 (2011).
Rogers, J. A., Jackman, R. J., Whitesides, G. M., Olson, D. L. & Sweedler, J. V. Using microcontact printing to fabricate microcoils on capillaries for high resolution proton nuclear magnetic resonance on nanoliter volumes. Appl. Phys. Lett. 70, 2464–2466 (1997).
Jackman, R. J., Rogers, J. A. & Whitesides, G. M . Fabrication of small-scale cylindrical articles. Patent: US 5951881 A (1999).
Bell, D. J., Dong, L., Nelson, B. J., Golling, M., Zhang, L. & Grützmacher, D. Fabrication and characterization of three-dimensional InGaAs/GaAs nanosprings. Nano Lett. 6, 725–729 (2006).
Huang, T., Liu, Z., Huang, G., Liu, R. & Mei, Y. Grating-structured metallic microsprings. Nanoscale 6, 9428–9435 (2014).
Mei, Y., Thurmer, D. J., Deneke, C., Kiravittaya, S., Chen, Y. F., Dadgar, A., Bertram, F., Bastek, B., Krost, A., Christen, J., Reindl, T., Stoffel, M., Coric, E. & Schmidt, O. G. Fabrication, self-assembly, and properties of ultrathin AlN/GaN porous crystalline nanomembranes: tubes, spirals, and curved sheets. ACS Nano 3, 1663–1668 (2009).
Smith, E. J., Makarov, D., Sanchez, S., Fomin, V. M. & Schmidt, O. G. Magnetic microhelix coil structures. Phys. Rev. Lett. 107, 097204 (2011).
Schmidt, O. G., Deneke, C., Kiravittaya, S., Songmuang, R., Heidemeyer, H., Nakamura, Y., Zapf-Gottwick, R., Müller, C. & Jin-Phillipp, N. Y. Self-assembled nanoholes, lateral quantum-dot molecules, and rolled-up nanotubes. IEEE J. Select. Top. Quantum Electron. 8, 1025–1034 (2002).
Yang, Z., Zhang, Y., Itoh, T. & Maeda, R. Flexible implantable microtemperature sensor fabricated on polymer capillary by programmable UV lithography with multilayer alignment for biomedical applications. J. Microelectromech. Syst 23, 21–29 (2014).
Anacleto, P., Mendes, P., Gultepe, E. & Gracias, D . 3D small antenna for energy harvesting applications on implantable micro-devices in Antennas and Propagation Conference (LAPC), 2012 Loughborough 1–4 IEEE, (2012).
Schmidt, O. G. & Eberl, K. Nanotechnology: Thin solid films roll up into nanotubes. Nature 410, 168 (2001).
Prinz, V. Y., Seleznev, V. A., Gutakovsky, A. K., Chehovskiy, A. V., Preobrazhenskii, V. V., Putyato, M. A. & Gavrilova, T. A. Free-standing and overgrown InGaAs/GaAs nanotubes, nanohelices and their arrays. Phys. E Low Dimens. Syst. Nanostruct 6, 828–831 (2000).
Luchnikov, V., Sydorenko, O. & Stamm, M. Self-rolled polymer and composite polymer/metal micro- and nanotubes with patterned inner walls. Adv. Mater. 17, 1177–1182 (2005).
Bassik, N., Abebe, B. T., Laflin, K. E. & Gracias, D. H. Photolithographically patterned smart hydrogel based bilayer actuators. Polymer 51, 6093–6098 (2010).
Troyk, P. R. Injectable electronic identification, monitoring, and stimulation systems. Annu. Rev. Biomed. Eng. 1, 177–209 (1999).
Melzer, M., Karnaushenko, D., Lin, G., Baunack, S., Makarov, D. & Schmidt, O. G. Direct transfer of magnetic sensor devices to elastomeric supports for stretchable electronics. Adv. Mater. 27, 1333–1338 (2015).
Mei, Y. F., Huang, G., Solovev, A. A., Bermúdez-Ureña, E., Mönch, I., Die, F., Reindl, T., Fu, R. K. Y., Chu, P. K. & Schmidt, O. G. Adv. Mater. 20, 4085 (2008).
Bof Bufon, C. C., Gonzlez, J. D. C., Thurmer, D. J., Grimm, D., Bauer, M. & Schmidt, O. G. Self-assembled ultra-compact energy storage elements based on hybrid nanomembranes. Nano Lett. 10, 2506 (2010).
Grimm, D., Bof Bufon, C. C., Deneke, C., Atkinson, P., Thurmer, D. J., Schäffel, F., Gorantla, S., Bachmatiuk, A. & Schmidt, O. G. Rolled-up nanomembranes as compact 3D architectures for field effect transistors and fluidic sensing applications. Nano Lett. 13, 213 (2013).
Böttner, S., Li, S., Jorgensen, M. R. & Schmidt, O. G. Vertically aligned rolled-up SiO2 optical microcavities in add-drop configuration. Appl. Phys. Lett. 102, 251119 (2013).
Martinez-Cisneros, C. S., Sanchez, S., Xi, W. & Schmidt, O. G. Ultracompact three-dimensional tubular conductivity microsensors for ionic and biosensing applications. Nano Lett. 14, 2219–2224 (2014).
Dastjerdi, M. H. T., Djavid, M. & Mi, Z. An electrically injected rolled-up semiconductor tube laser. Appl. Phys. Lett. 106, 021114 (2015).
Jamal, M., Zarafshar, A. M. & Gracias, D. H. Differentially photo-crosslinked polymers enable self-assembling microfluidics. Nature Commun 2, 527 (2011).
Bansal, R . in Handbook of Engineering Electromagnetics 259 (Springer Science & Business, 2004).
Slobozhanyuk, A., Lapine, M., Powell, D. A., Shadrivov, I. V., Kivshar, Y. S., McPhedran, R. C. & Belov, P. A. Flexible helices for nonlinear metamaterials. Adv. Mater. 25, 3409 (2013).
Yan, C., Xi, W., Si, W., Deng, J. & Schmidt, O. G. Highly conductive and strain-released hybrid multilayer Ge/Ti nanomembranes with enhanced lithium-ion-storage capability. Adv. Mater. 25, 539 (2013).
Deng, J., Ji, H., Yan, C., Zhang, J., Si, W., Baunack, S., Oswald, S., Mei, Y. & Schmidt, O. G. Naturally rolled-up C/Si/C trilayer nanomembranes as stable anodes for lithium-ion batteries with remarkable cycling performance. Angew. Chem. 125, 2382–2386 (2013).
Mönch, I., Makarov, D., Koseva, R., Baraban, L., Karnaushenko, D., Kaiser, C., Arndt, K. F. & Schmidt, O. G. Rolled-up magnetic sensor: nanomembrane architecture for in-flow detection of magnetic objects. ACS Nano 5, 7436 (2011).
Mei, Y., Solovev, A. A., Sanchez, S. & Schmidt, O. G. Rolled-up nanotech on polymers: from basic perception to self-propelled catalytic microengines. Chem. Soc. Rev. 40, 2109–2119 (2011).
Acknowledgements
We thank I Fiering and C Krien (IFW Dresden) for their assistance with the deposition of the metal layer stacks. The support in the development of the experimental setups from the research technology department of the IFW Dresden and the clean room team headed by Dr S Harazim (IFW Dresden) is greatly appreciated. This work is financed in part by the European Research Council within the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 306277.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies the paper on the NPG Asia Materials website
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Karnaushenko, D., Karnaushenko, D., Makarov, D. et al. Compact helical antenna for smart implant applications. NPG Asia Mater 7, e188 (2015). https://doi.org/10.1038/am.2015.53
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/am.2015.53
This article is cited by
-
Self-assembly of Co/Pt stripes with current-induced domain wall motion towards 3D racetrack devices
Nature Communications (2024)
-
Tailoring electron beams with high-frequency self-assembled magnetic charged particle micro optics
Nature Communications (2022)
-
Self-assembly as a tool to study microscale curvature and strain-dependent magnetic properties
npj Flexible Electronics (2022)
-
A new dimension for magnetosensitive e-skins: active matrix integrated micro-origami sensor arrays
Nature Communications (2022)
-
A flexible microsystem capable of controlled motion and actuation by wireless power transfer
Nature Electronics (2020)