Abstract
Aims
To validate the use of Orbscan II slit-scanning topography for measuring posterior corneal curvature, by comparing corneal power calculations using this value with the standard keratometric method of corneal power calculation.
Method
Corneal measurements were taken from both eyes of 15 normal subjects using the Javal–Schiotz keratometer and the Orbscan II topographer. Corneal power was calculated using standard keratometric indices of 1.337.5 or 1.331.5 and Javal–Schiotz keratometry. Corneal power was then recalculated using the thick-lens formula, with anterior corneal curvature from the Javal–Schiotz or Orbscan II and posterior measurements from the Orbscan II; in addition, the 3.0 mm ‘Mean Power’ value from the Orbscan II software was noted. Six comparisons were then made using mean–difference plots.
Results
The smallest difference and therefore the most predictable agreement was between Javal–Schiotz keratometry using a refractive index of 1.331.5 and the thick-lens formula using Javal–Schiotz anterior curvature and Orbscan II posterior curvature. The mean difference was 0.27 D with a confidence interval of 0.02–0.52 D.
Conclusions
In normal eyes, data on posterior corneal curvature from the Orbscan II can be used to calculate corneal power in close agreement with the standard keratometric method. This suggests the use of the Orbscan II in eyes that have previously undergone refractive surgery, for calculation of intraocular lens power prior to cataract surgery.
Similar content being viewed by others
Introduction
Intraocular lens (IOL) power calculation for cataract surgery is problematic in patients who have previously undergone corneal refractive surgery. The difficulty arises from the inability to measure posterior corneal curvature. Instead, corneal power is estimated from the anterior corneal curvature alone using an approximation that considers the cornea as a single refracting surface, with two parameters, radius and refractive index. This assumes a relationship between the anterior and posterior corneal curvatures. Following excisional refractive surgery, for example, excimer laser photorefractive keratectomy (PRK) and laser in situ keratomileusis (LASIK), the anterior surface is flattened, while the posterior surface is unchanged or may even steepen slightly.1 Clearly, the relationship between the anterior and posterior surfaces is altered by such surgery.
Laser refractive surgery for myopia reduces the converging power of the anterior surface while retaining the diverging power of the posterior surface. Thus, calculation of the total corneal power from anterior surface measurements alone underestimates the reduction in power. The net effect of this is to underestimate the IOL power required, resulting in relative postoperative hyperopic refraction.2
The Orbscan II (Orbtek, Salt-Lake City, UT, USA) is a scanning slit-beam topographer that measures posterior corneal elevation and thereby curvature. If this measurement were to be validated, then determination of corneal power after refractive surgery would be greatly simplified.
This study aimed to test the validity of slit-scan topography measurement of posterior corneal curvature in normal eyes by using it to calculate corneal power, and comparing this result to the corneal power calculated using Javal–Schiotz keratometry.
Methods
Fifteen normal subjects with no history of corneal disease or ocular surgery underwent Javal–Schiotz keratometry and slit-scan topography, performed by the author. Javal–Schiotz keratometry was recorded to the nearest 0.05 mm. Slit-scan topography-simulated keratometry was recorded to 0.01 mm.
Calculation of corneal power
Single refracting surface assumption
Corneal power may be estimated considering the cornea as a single refracting surface of negligible thickness. Refractive indices of 1.3375 (the standard keratometric index (SKI) designated by Javal) and 1.3315 (the refractive index recommended by Gullstrand in his schematic eye and independently by Olsen3) are used in this study, designated ‘Javal 337.5’ and ‘Javal 331.5’, respectively.
Thick-lens formula calculation
The total optical power of the cornea may be calculated according to the formula for thick lenses:4

where

with n1 being the refractive index of air (1.0), n2 the refractive index of cornea (1.376), n3 the refractive index of aqueous (1.336), and t the corneal thickness (m).
For this study, power is calculated using slit-scan topography data for r1, r2 and corneal thickness (‘Orbscan Power’), or using Javal–Schiotz keratometry for r1 and slit-scan topography for r2 and corneal thickness (‘Orbscan/Javal Power’). The Orbscan II proprietary software package also calculates the total corneal power averaged across the central 3 mm of cornea; this result is presented as ‘Orbscan Mean Power’.
Data comparison
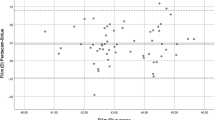
This study compares two methods of measuring a parameter for which the true result is unknown. Assessment of agreement between the two methods is therefore best assessed using Bland–Altman mean–difference plots5 (Figure 1a–f). For each plot, mean total corneal power, calculated as the arithmetic mean of the two methods being assessed is plotted (x-axis) against the difference between the two methods (y-axis). This allows analysis of any systematic difference between the methods (from the mean of the differences) and the consistency of any difference (the spread of the differences), including altered relationship between methods as the mean is varied.
Mean-difference plots comparing the methods of corneal power calculation. In each case, the arithmetic mean of the two powers is plotted on the x-axis, and the difference between the two powers is plotted on the y-axis. The dashed lines equal no difference. The spread of data is least for plots using Orbscan to measure r2 and Javal-Schiotz for r1 (c & d); agreement is closest using 1.331.5 as the keratometric index (d).
Six comparisons were made: ‘Javal 337.5’ was compared with ‘Orbscan Power (Figure 1a), ‘Orbscan/Javal Power’ (Figure 1b), and ‘Orbscan Mean Power’ (Figure 1c). ‘Javal 331.5’ was compared with ‘Orbscan Power’ (Figure 1d), ‘Orbscan/Javal Power’ (Figure 1e), and ‘Orbscan Mean Power’ (Figure 1f), all as defined above.
Data from both eyes are presented in the plots; only right eye data were used for calculations of the mean keratometry, simulated keratometry, and mean and standard error of differences between methods. A two-tailed paired t-test was used to compare keratometry and simulated keratometry. All calculations and data plots were performed on Excel 97 (Microsoft, Seattle, WA, USA).
Results
Patients
In all patients, both keratometry and slit-scan topography were possible. The mean keratometry was 7.92 mm (SD 0.28) and topographic simulated keratometry was 8.08 mm (SD 0.28) (P<0.001). The mean topographic simulated posterior curvature was 6.67 mm (SD 0.26).
Mean–difference plots
The six mean–difference plots are shown in Figure 1. Mean and standard deviations of power and difference between powers are given in Table 1.
The smallest confidence interval of differences (0.02–0.52 D) and therefore most predictable agreement was between the ‘Javal 331.5’ and the ‘Orbscan/Javal Power’ (Figure 1e). The ‘Javal 331.5’ power was a mean of 0.27 D less than the ‘Orbscan/Javal Power’.
Discussion
A number of methods have been described to calculate corneal power following refractive surgery.6,7 The peroperative data method8 requires knowledge of the preoperative keratometry and refraction, and stable post-excimer laser refraction prior to the development of cataract. If pre- and post-laser keratometry is known, then an estimate of corneal power can be made using the thick-lens formula assuming that the posterior corneal curvature does not change.6,9 If these preoperative data are unavailable, as is often the case, the hard contact lens method10 must be used. The difference between unaided and plano-contact lens over-refraction spherical equivalent refractions is subtracted from the base curve power of the contact lens to determine effective corneal power. This requires reasonable visual acuity for accurate subjective refraction, which may not be present in the precataract surgery situation, and may be rendered inaccurate by irregularities of corneal shape and/or disruption to the tear lens under the contact lens.
The difficulties inherent in these methods result in the recommendation to perform all possible calculations and then use the lowest corneal power that results in order to err on the side of a myopic outcome.9 Unfortunately, any significant postoperative error is likely to result in dissatisfaction in a group of patients who have previously undergone the risks and financial costs of surgery in order to achieve emmetropia. A more accurate method of corneal power calculation is therefore required.
Hamed et al9 estimated posterior corneal curvature in eyes prior to LASIK, assuming that posterior curvature was related to anterior curvature by a factor of 6.8/7.7. Assuming no change in the posterior corneal power, they calculated post-LASIK power, and compared it with that determined by the refractive history method. They found reasonable agreement (SD of differences 0.66). This method does, however, like the refractive history method, require knowledge of pre-LASIK corneal curvature. In addition, it assumes stability of the posterior corneal shape following LASIK, which is disputed.1 Clearly, direct measurement of the posterior corneal curvature would be preferable to making the assumptions described above.
The keratometer uses the tear film on the anterior corneal surface as a convex mirror.4 At a fixed working distance, the object size is adjusted to form the first Purkinje image of a constant size, object size is inversely proportional to curvature. For, an average eye, only the central 3.2 mm of cornea contributes to the reading. Owing to the small difference in refractive indices between the cornea and aqueous, the image from the posterior cornea is too faint to allow measurement of curvature.
The Orbscan II calculates corneal elevation by triangulating between the edge of an illuminating beam of known (calibrated) position and the back-scattered light emitted perpendicular to the instrument. The corneal elevation between adjacent points is interpolated as a section of a sphere and local curvature calculated as the average curvature in all directions at that point. Curvature over the central 3 mm is averaged to generate simulated keratometry, and is possible for both anterior and posterior corneal surfaces.
Direct validation of slit-scan topography posterior corneal measurement has not been possible so far. Slit-scan topography-calculated total optical power change has been demonstrated to correlate well with refractive change following myopic LASIK (correlation coefficient=0.835, P<0.04).11
From this study, it can be stated that slit-scan topography measurement of posterior corneal curvature and subsequent calculation of corneal power is in close agreement with that calculated using the Javal–Schiotz keratometer and the single refracting surface approximation. The best agreement was obtained using a refractive index of 1.3315 for the keratometric calculation, and Javal–Schiotz anterior corneal keratometry in conjunction with Orbscan posterior corneal curvature for the thick-lens formula calculation. IOL power calculation with the SRK/T formula using either method is clinically interchangeable (approximately 0.3 D difference in IOL power selection for emmetropia in an average eye). Using the ‘Mean Power’ calculated by the Orbscan II software led to worse agreement than calculating power using the thick-lens formula as described above. It is not clear from the Orbscan II technical data how the ‘Mean Power’ is calculated, and the manufacturers were unable to provide information as to the reason for the disparity.
Use of slit-scan topography-simulated anterior corneal curvature in the thick-lens formula results in less good agreement with the standard Javal–Schiotz measurement of corneal power than substituting the keratometric anterior corneal curvature. Javal–Schiotz keratometry has been demonstrated to be highly accurate and repeatable in normal corneas. 12 Following refractive surgery, loss of sphericity of the central cornea reduces its reliability, and automated keratometry and videokeratoscopy have been suggested to be more accurate. 13 Orbscan II consistently measured flatter keratometry than did the Javal–Schiotz keratometer, used in IOL power calculation after refractive surgery, which would tend towards myopic error. For these two reasons, following refractive surgery, slit-scan topography might generate a better value for anterior corneal curvature than the Javal–Schiotz keratometer.
Conclusions
Orbscan II measurement of posterior corneal curvature may be used to calculate corneal power in normal eyes, using the thick-lens formula. The same methodology could be applied to corneal power calculation after refractive surgery, comparing the perioperative data method of corneal power calculation with Orbscan II power calculation. If good agreement can again be demonstrated, then the current difficulties in IOL selection in patients with prior refractive surgery may be overcome.
References
Seitz B, Torres F, Langenbucher A, Behrens A, Suárez E . Posterior corneal curvature changes after myopic laser in situ keratomileusis. Ophthalmology 2001; 108: 666–673.
Seitz B, Langenbucher A, Nguyen N, Kus M, Küchle M . Underestimation of intraocular lens power for cataract surgery after myopic photorefractive keratectomy. Ophthalmology 1999; 106: 693–702.
Olsen T . On the calculation from curvature of the cornea. Br J Ophthalmol 1986; 70: 152–154.
Elkington F, Frank H . Clinical Optics, 2nd ed. Blackwell Scientific Publications: oxford, 1991.
Bland JM, Altman DG . Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986; 1: 307–310.
Speicher L . Intraocular lens calculation status after corneal refractive surgery. Curr Opin in Ophthalmol 2001; 12: 17–29.
Seitz B, Langenbucher A . Intraocular lens power calculation in eyes after corneal refractive surgery. J Refract Surg 2000; 16: 349–360.
Holladay JT . Consultations in refractive surgery. Refract Corneal Surg 1989; 5: 203.
Hamed A, Wang L, Misra M, Koch D . A comparative analysis of five methods of determining corneal refractive power in eyes mat have undergone myopic laser in situ keratomileusis. Ophthalmology 2002; 109: 651–658.
Holladay JT . Cataract surgery in patients with previous keratorefractive surgery (RK, PRK and LASIK). Ophthalmic Pract 1997; 15: 238–244.
Srivannaboon S, Reinstein D, Sutton H, Holland S . Accuracy of Orbscan total optical power maps in detecting refractive change after myopic laser in situ keratomileusis. J Cataract Refract Surg 1999; 25: 1596–1599.
Sunderraj P . Clinical comparison of automated and manual keratometry in pre-operative ocular biometry. Eye 1992; 6: 60–62.
Varssano D, Rapuano CJ, Luchs JL . Comparison of keratometric values of healthy and diseased eyes measured by Javal keratometer, EyeSys and PAR. J Cataract Refract Surg 1997; 23: 419–422.
Author information
Authors and Affiliations
Additional information
Poster presented at the Royal College of Opthalmologists, Annual Congress, Manchester, 21–23 May 2002
Rights and permissions
About this article
Cite this article
Leyland, M. Validation of Orbscan II posterior corneal curvature measurement for intraocular lens power calculation. Eye 18, 357–360 (2004). https://doi.org/10.1038/sj.eye.6700659
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/sj.eye.6700659
Keywords
This article is cited by
-
Assessment of total corneal power after myopic corneal refractive surgery in Chinese eyes
International Ophthalmology (2019)