Abstract
Background:
Three lung cancer (LC) models have recently been constructed to predict an individual's absolute risk of LC within a defined period. Given their potential application in prevention strategies, a comparison of their accuracy in an independent population is important.
Methods:
We used data for 3197 patients with LC and 1703 cancer-free controls recruited to an ongoing case–control study at the Harvard School of Public Health and Massachusetts General Hospital. We estimated the 5-year LC risk for each risk model and compared the discriminatory power, accuracy, and clinical utility of these models.
Results:
Overall, the Liverpool Lung Project (LLP) and Spitz models had comparable discriminatory power (0.69), whereas the Bach model had significantly lower power (0.66; P=0.02). Positive predictive values were highest with the Spitz models, whereas negative predictive values were highest with the LLP model. The Spitz and Bach models had lower sensitivity but better specificity than did the LLP model.
Conclusion:
We observed modest differences in discriminatory power among the three LC risk models, but discriminatory powers were moderate at best, highlighting the difficulty in developing effective risk models.
Similar content being viewed by others
Main
Worldwide, an estimated 1.35 million new lung cancer (LC) cases and 1.18 million LC-related deaths occur every year (Parkin et al, 2005). It has been suggested that ∼70% of all LCs could be prevented by reducing the prevalence of major risk factors, particularly smoking (Danaei et al, 2005). Given that LC risk differs greatly among smokers, the ability to estimate an individual's absolute risk could be used to guide preventive interventions. In particular, absolute risk scores could be used both to motivate individuals to reduce their LC risk through behaviour and lifestyle modifications and to refine selection of participants for LC screening trials on the basis of maximising benefit (Vickers et al, 2006; Duffy et al, 2009). Other cancers that have well-known risk-prediction models include breast (Gail et al, 1989; Tyrer et al, 2004; Tice et al, 2005), colorectal (Imperiale et al, 2000; Selvachandran et al, 2002), melanoma (Cho et al, 2005; Fears et al, 2006), ovarian (Hartge et al, 1994), and bladder cancers (Wu et al, 2007).
Within the last decade, three models to estimate an individual's absolute LC risk were developed: the Bach (Bach et al, 2003), Spitz (Spitz et al, 2007), and the Liverpool Lung Project (LLP) models (Cassidy et al, 2008). All the three models share risk factors (such as smoking duration and occupational exposure to asbestos); however, differences arise, with the inclusion of lung-related comorbidities or family history information. These models have not previously been compared in an independent data set in terms of discriminatory power, accuracy, and clinical utility. Such a comparison, to evaluate whether these published risk models have similar discriminatory power for a given population of individuals, is important, given the potential application of risk-prediction models to strategies for primary and secondary preventions.
In this study, we used each of these models to estimate 5-year absolute LC risks for an independent population of LC patients and healthy controls. We compared the discriminatory power of these three models by calculating the area under the curve (AUC) of the receiver operator characteristic (ROC) curve for each 5-year absolute risk estimate. We evaluated the accuracy and compared the positive predictive value (PPV; the probability of accurately categorising an affected participant) and the negative predictive value (NPV; the probability of accurately categorising an unaffected participant) among the three risk models; we also evaluated the clinical utility of each.
Materials and methods
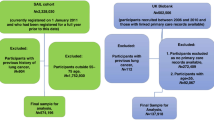
A total of 4900 LC patients and controls were accrued for this study, 3197 were treated in the Thoracic Surgery, Thoracic Oncology, or Pulmonary Units at the Massachusetts General Hospital (MGH) (Boston, MA, USA). Starting in 1992, enrolment was initially restricted to patients with operable LC; however, case definition was expanded in August 1996 to include inoperable LC to reflect the full spectrum of LC patients. Lung cancer diagnosis was histologically confirmed by a lung pathologist. Controls (N=1703) were LC-free individuals initially accrued from among family members or friends of cases, but accrual was subsequently expanded to include friends and family (not blood related to study cases) of individuals being treated at the MGH for non-LC diseases (Xu et al, 1996; Garcia-Closas et al, 1997; Wang et al, 2001).
Inclusion of risk factors in the three LC risk models is summarised in Table 1. Smokers were defined as those who had smoked >400 cigarettes in their lifetime; former smokers were those who had quit smoking at least 1 year before the cancer diagnosis (patients) or the interview (controls). Smoking duration was determined by subtracting the age at which the participant had started smoking from either the age at which the participant had quit smoking (former smokers) or the participant's current age (current smokers). Pack-years were calculated by multiplying the smoking duration (in years) by the number of cigarettes smoked per day and then dividing by 20. Time of smoking cessation for former smokers was determined by subtracting the age at which the participant had quit smoking from the participant's current age.
Participants were classified as positive for asbestos exposure if they had been directly exposed for at least 8 h per week for a year or if they were employed in an asbestos-related industry (according to the Standard Industrial Classification Manual (1972) and/or the Dictionary of Occupational Titles (1991)). Exposure to wood dusts (including sawdust or sanding dust) for at least 8 h per week for a year was self-reported, or for a family history of any cancer if at least two first-degree relatives had cancer. Participants were classified as positive for a family history of any smoking-related cancer if at least one first-degree relative had had cancer at some point in his or her life. Participants were also classified by self-reported physician-diagnosed emphysema or hay fever at any time before study entry (Spitz) or by physician-diagnosed pneumonia at least 2 years before entry (LLP).
Any study participant with missing data for any of the risk factors for any model was excluded from analysis. As all three models were developed using data obtained from White participants, we only included individuals who self-reported being non-Hispanic White. For the comparison of discriminatory power between the LLP and Bach models and the Spitz and Bach models only ever smokers (total of 1066 LC and 677 controls) were used as the Bach model was developed only for ever smokers (Bach et al, 2003). In the comparison between the LLP and Spitz models, never, former, and current smokers were included (total of 1121 LC and 1024 controls).
The institutional review boards at the M. D. Anderson Cancer Center, MGH, and the Harvard School of Public Health approved this study.
We calculated the 5-year absolute risk of LC for the three models, using MatLab software (The MathWorks Inc., Natick, MA, USA). For the Bach model, they were obtained by running 1-year incidence and mortality models recursively five times, with each individual contributing to the predicted risk for 5 years. For the Spitz and LLP models, they were estimated by combining the risk of cancer from the relative risk model with age- and gender-specific LC incidence rates.
Details regarding the exact calculation of risk for each model were given in the original paper (Bach et al, 2003; Spitz et al, 2007; Cassidy et al, 2008). With the LLP model, the α-value used to calculate the 5-year absolute risk was adjusted for the US LC incidence rate (Appendix Table A1). For each participant, we had three estimates of absolute risk for LC (one from each model). For each model, we used NCSS statistical software (NCSS, Kaysville, UT, USA) to calculate the specificity and sensitivity required to construct ROC curves and estimate AUC (binomial method) and the 95% confidence interval (95% CI) for each of the three models. We also calculated the AUC after stratification of participants by sex and age (<50 vs ⩾50 years). We then conducted pairwise comparisons of the AUCs of the three models using the method described in the NCSS package (Hanley and McNeil, 1983), the test statistic for comparing two ROC curves being given by

where AUCi is the area under the ROC curve from the ith model (i=1,2), s.e.i the s.e. of AUCi, and r the correlation between AUC1 and AUC2 (Tyrer et al, 2004). The test statistic z follows a standard normal distribution; and values of z>z1−α are interpreted as evidence that AUC1 is significantly greater than AUC2 for the given α-level.
From these risk factors, a relative risk was calculated and combined with age- and gender-specific incidence rates from x (SEER) (SEER, 2005), and all-cause mortality (excluding LC) rates from CDC (Centers for Disease Control) to estimate the absolute risk of LC (National Center for Health Statistics, 2003) (Appendix Table A2). As most of the absolute risk calculations involve pairwise comparisons from three different LC models, the Bonferroni correction was taken into account to adjust for any multiple comparisons issues.
We calculated the PPV and NPV for each of the models (Spitz, Bach, and LLP) separately for all participants and then stratified them by smoking status (former and current). We conducted pairwise comparisons (Spitz vs LLP, Spitz vs Bach, and Bach vs LLP) of the PPV and NPV to test differences of these two statistics among the three models using the normal approximation to the test of two proportions. As with the absolute risk results, the Bonferroni correction was used for both the PPV and the NPV to adjust for multiple testing. Clinical utility of the models was evaluated using scaled rectangle diagrams as implemented in the Search Partition Analysis (SPAN, Auckland, New Zealand) program (Marshall, 2001, 2005, 2009). Scaled rectangle diagrams display the joint occurrence of attributes (namely risk for disease) for a risk model and true disease status and provide a visual presentation of how well a model discriminates. With these diagrams, the white rectangle represents all individuals, the green rectangle represents all cases, and the blue, purple, and red rectangles represent individuals with three increasing levels of LC risk (2.5, 5, and 7.5%, respectively). Models with high clinical utility will have the vast majority of their cases, have higher levels of risk, and have fewer controls with those individuals at the higher LC absolute risk.
Results
The epidemiological and demographic data for the validation set of 1066 LC patients and 677 controls are presented in Table 2. Patients (mean age, 64.8 years) were older than controls (mean age, 61.1 years; P<0.001). The majority of patients (58%) and controls (52%) were male. There was a higher percentage of former smokers among controls (74.2%) than among patients (56.2%; P<0.001). Lung cancer patients who were current smokers smoked significantly more cigarettes per day (mean, 29.9), and had smoked for longer periods (mean, 43.8 years) than did controls (mean cigarettes smoked per day: 21.1, P<0.001; smoking duration: 38.5 years, P<0.001). Similarly, patients who were former smokers had smoked significantly more cigarettes per day (mean, 30.6) and had smoked for longer periods (mean, 34.8 years) than did controls (mean cigarettes smoked per day: 22.9, P<0.001; smoking duration: 24.2 years, P<0.001). Lung cancer patient pack-years were over 24 units higher in both current and former smokers than in controls, and these differences were highly significant in both smoking groups (P<0.001). Controls reported longer quitting durations (mean, 19.8 years) than did patients (mean, 14.1 years; P<0.001). Former smokers more after reported a family history of any cancer (34.4%) and smoking-related cancers (30.6%) than did controls (any cancer: 27.9%, P=0.023; smoking-related cancers: 22.9%, P=0.005); and current smokers reported a significantly higher percentage of smoking-related cancers (30.4%) than did controls (22.3%, P=0.049).
The discriminatory power for the three models, overall and stratified by smoking, age, and sex, are summarised in Table 3, the AUCs being 0.69 for the Spitz (95% CI=0.66–0.71) and LLP (95% CI=0.67–0.71) models and 0.66 (95% CI=0.64–0.69) for the Bach model. The differences in discriminatory power between the LLP and Bach models were significant (P=0.023), and the differences between the Spitz and Bach models reached borderline significance (P=0.072). Among former smokers, the discriminatory power was 0.70 (95% CI=0.67–0.73) for the Spitz and LLP models and 0.65 (95% CI=0.62–0.68) for the Bach model. Among current smokers, the discriminatory power was 0.68 (95% CI=0.64–0.72) for the Spitz model, 0.65 (95% CI=0.60–0.69) for the Bach model, and 0.66 (95% CI=0.62–0.70) for the LLP model. Among former smokers, the Bach model was outperformed by both the LLP (P=0.002) and the Spitz (P=0.008) models, whereas among current smokers, only the Spitz model significantly outperformed the Bach model (P=0.024). When incorporating never smokers for testing discriminatory power, the LLP model (AUC=0.72, 95% CI=0.70–0.74) outperformed the Spitz model (AUC=0.68, 95% CI=0.66–0.71) significantly (P=0.001).
We also tested the discriminatory power of all models when participants were stratified by age and sex (Table 3) and for women over the age of 50 years, observed significant differences in discriminatory power between the Spitz and Bach models, and the LLP and Bach models.
Table 4 summarises the NPV and PPV results for each. Overall, the three models had reasonable PPV levels (all >70%); the Spitz model had a significantly higher PPV (88.2%) than those of the LLP (75.9%; P<0.001) and the Bach (80.9%; P=0.009) models. Among former smokers, the Spitz model had significantly higher PPV (85.5%) than did the LLP model (72.6%; P<0.001) but not significantly higher PPV than the Bach model (83.6%; P=0.851). However, among current smokers, the Spitz model had higher PPV (91.9%) than did the Bach (80.4%; P=0.002) and the LLP (80.9%; P<0.001) models. The overall NPV for each of the three models were lower than the PPV (range=45.0–56.0%), with the LLP model having a substantially better probability of accurately categorising an unaffected participant. The LLP model was also significantly better for the NPV among former smokers, but both the Spitz and Bach models were competitive with the LLP model in calculating the NPV among current smokers.
To demonstrate the clinical utility of each model, Table 5 presents the percentages of patients and controls with LC risk estimates of >2.5, 5, and 7.5% as determined by each model. Using a cutoff of >2.5% risk as an example, the percentages of LC patients that were correctly identified by the Spitz, Bach, and LLP risk models were 26.6, 30.2, and 66.7%, respectively. The percentages of controls with >2.5% risk that were incorrectly identified as LC patients by the Spitz, Bach, and LLP risk models were 5.6, 11.2, and 33.4%, respectively. For all three models, setting a higher risk cutoff resulted in a lower proportion of controls being incorrectly identified as LC patients and a lower proportion of LC patients being correctly identified. This is evident in the scaled rectangle diagrams for the Spitz, Bach, and LLP risk models at cutoffs of >2.5, 5, and 7.5% absolute risk, respectively (Figure 1). Using the >2.5% risk cutoff, the LLP model identified 276 LC patients who were not identified by the Spitz and Bach models, but it also incorrectly identified 139 controls as LC patients. Although the Spitz and Bach models identified fewer LC patients (17 and 15, respectively), significantly fewer controls were incorrectly identified as patients (5 and 8, respectively) compared with the LLP model. Using the >7.5% risk cutoff, the Spitz model had 100% specificity, but its sensitivity was impractically low (2.2%). At this level of risk, for every four LC patients correctly identified by the LLP model, one control was incorrectly identified as a LC patient, wherein as the equivalent patient-to-control ratio for the Bach model was 5 to 1.
Clinical utility of the Spitz, Bach, and LLP models. Scaled rectangle diagrams for (A) the Spitz, (B) Bach, and (C) LLP risk models at defined levels of lung cancer risk. For each colour of the diagram: white equals all controls with <2.5% risk, and green equals all cases with <2.5% risk. Blue represents all individuals with at least 2.5% risk, but <5% risk. Purple represents all individuals with at least 5.0% risk, but <7.5% risk. Red represents all individuals with at least 7.5% risk.
Discussion
The purpose of this analysis was to compare the discriminatory power and accuracy of three LC risk-prediction models using an external set of LC cases and controls. We observed that the Spitz and LLP models had similar abilities to discriminate between former and current smoking cases and controls and that each of these models outperformed the Bach model. The Spitz and LLP models incorporated population-based incident LC rates, which could account for their better discriminatory power than that of the Bach model. For every 5-year age group from 20 to 89 years, we incorporated the SEER rates for the incidence of LC and the mortality rates from all causes other than LC (Appendix Table A1). In terms of model accuracy, the Spitz model had higher PPV than did the LLP and Bach models among both types of ever smokers, but the LLP model outperformed both the Spitz and Bach models in terms of the NPV. In terms of clinical utility, the Spitz model had the lowest false-positive rate for risk estimates >2.5%, whereas the LLP model had the highest false-positive rate. At all levels of risk, the LLP model correctly identified a higher proportion of LC patients than did the other models did but also incorrectly identified a higher proportion of controls as LC patients.
Each model included some form of tobacco exposure. In the Bach model, the variables – duration of smoking (in years) and number of cigarettes smoked per day – are included for both former and current smokers. In the Spitz model (controls matched to cases on smoking status), the duration of smoking and numbers of cigarettes smoked per day are combined into pack-years for current smokers only and into age at smoking cessation for former smokers. The Bach and LLP models do not include a smoking cessation variable. The Bach model included smokers aged 50–75 years who are/were heavy smokers (10–60 cigarettes per day for 25–60 years) and who had quit no more than 20 years previously (Bach et al, 2003).
In terms of clinical utility, the Spitz and Bach models performed reasonably well in identifying LC patients at defined levels of risk while limiting the number of false-positive results. However, the LLP model was much better at identifying individuals with LC but also had a much higher false-positive rate than the Spitz and Bach models had. This could be attributed to the importance of smoking in the LLP model. The Spitz model's relatively low recognition of cancer patients with a >2.5% absolute LC risk could be caused by smoking being a matching variable in the model rather than a risk factor. The overall high (>75%) PPVs for the three models indicate that they can identify high-risk individuals; however, the overall relatively low NPVs (between 45 and 56%) indicate that many low-risk individuals would be identified as well. The scaled rectangle diagrams illustrate more clearly the modest discriminatory performances of the Spitz, Bach, and LLP models and provide a sobering message about LC risk prediction. To substantially improve LC risk discriminatory power for individual patients, we need to identify a risk factor (other than smoking habits) that has a different distribution in LC patients from those who will not develop it; to date, there is no evidence for such a factor. High expectations have been pinned on genome-wide association studies, which have successfully identified hundreds of common genetic variants that are strongly associated with the risk of more than 40 diseases, including LC (Kraft and Hunter, 2009). However, a strong association does not necessarily guarantee good classification or discriminatory ability (Jakobsdottir et al, 2009). It was recently shown that on average, 80 common variants with odds ratios of 1.25 each were required to develop a model useful for the identification of high-risk individuals (AUC>0.80) for genetic profiling studies (Janssens et al, 2006).
Our study had some limitations. The most important limitation is that the study design is a case–control study, which could lead to some recall bias with the self-reported variables, such as smoking and environmental tobacco smoke exposure (Asomaning et al, 2008). However, in this study, controls were recruited from family and friends of those being treated for LC at the MGH, so that exposures for the self-reported variables would be similar or non-differential, among cases and controls, which would limit recall bias (Miller et al, 2003). With non-differential biases, AUC results will regress to the null, so it is possible that the AUC results are conservative instead of overstated (Greenland and Lash, 2008).
Other minor limitations include that the risk-prediction models compared in our study were developed in Caucasian populations, so the validation was also restricted to Caucasians, and thus, the models may not be applicable to other racial or ethnic groups. In addition, for most of the analysis, we only included ever-smoker cases and controls in our analysis, and thus, the enormous contribution of smoking to LC risk was effectively underestimated. The ultimate test of a model's application is its accurate prediction of risk in an independent data set. However, direct comparison of risk models is complicated by the fact that few studies have population samples that are large enough and diverse enough in age and risk factor backgrounds (Cassidy et al, 2007). Thus, to avoid possible information bias, it was imperative for our analysis to select only patients and controls from those who had complete information relating to risk-model covariates.
Despite these limitations, our analyses showed that LC risk-prediction models performed reasonably well when compared with each other in an independent validation set. All models include biologically plausible and well-established risk factors that have been shown to be significant in previous studies. One possible caveat is that the discriminatory values do not exceed 0.75, a value that has been suggested for the screening of individuals with an increased risk of disease (Janssens et al, 2007). This relatively low discriminatory value suggests that there is much work yet to be accomplished in LC risk prediction, especially compared with other cancer risk models such as colorectal cancer, which has a concordance statistic between 0.84 and 0.86 (Selvachandran et al, 2002). However, the discriminatory power results for LC compare favourably with those models for breast cancer (0.58–0.68) and melanoma (0.62) (Rockhill et al, 2003; Cho et al, 2005; Tice et al, 2005). Future improvements in the discriminatory ability of LC risk models may be possible by the incorporation of biomarkers related to LC risk, top hits from genome-wide association studies, rare variants, or a combination of these with lifestyle and environmental risk factors. Improved LC risk models offer an enormous potential benefit to guide the physician's and the patient's perception of individual risk of disease.
Change history
29 March 2012
This paper was modified 12 months after initial publication to switch to Creative Commons licence terms, as noted at publication
References
Asomaning K, Miller DP, Liu G, Wain JC, Lynch TJ, Su L, Christiani DC (2008) Second hand smoke, age of exposure and lung cancer risk. Lung Cancer 61: 13–20
Bach PB, Kattan MW, Thornquist MD, Kris MG, Tate RC, Barnett MJ, Hsieh LJ, Begg CB (2003) Variations in lung cancer risk among smokers. J Natl Cancer Inst 95: 470–478
Cassidy A, Duffy SW, Myles JP, Liloglou T, Field JK (2007) Lung cancer risk prediction: a tool for early detection. Int J Cancer 120: 1–6
Cassidy A, Myles JP, van Tongeren M, Page RD, Liloglou T, Duffy SW, Field JK (2008) The LLP risk model: an individual risk prediction model for lung cancer. Br J Cancer 98: 270–276
Cho E, Rosner BA, Feskanich D, Colditz GA (2005) Risk factors and individual probabilities of melanoma for Whites. J Clin Oncol 23: 2669–2675
Danaei G, Vander Hoorn S, Lopez AD, Murray CJL, Ezzati M (2005) Causes of cancer in the world: comparative risk assessment of nine behavioural and environmental risk factors. Lancet 366: 1784–1793
Duffy SW, Raji OY, Agbaje OF, Allgood PC, Cassidy A, Field JK (2009) Use of lung cancer risk models in planning research and service programmes in CT screening for lung cancer. Expert Rev Anticancer Ther 9: 1467–1472
Fears TR, Guerry IV D, Pfeiffer RM, Sagebiel RW, Elder DE, Halpern A, Holly EA, Hartge P, Tucker MA (2006) Identifying individuals at high risk of melanoma: a practical predictor of absolute risk. J Clin Oncol 24: 3590–3596
Gail MH, Brinton LA, Byar DP, Corle DK, Green SB, Schairer C, Mulvihill JJ (1989) Projecting individualized probabilities of developing breast cancer for White females who are being examined annually. J Natl Cancer Inst 81: 1879–1886
Garcia-Closas M, Kelsey KT, Wiencke JK, Xu X, Wain JC, Christiani DC (1997) A case–control study of cytochrome P450 1A1, glutathione S-transferase M1, cigarette smoking and lung cancer susceptibility. Cancer Causes Control 8: 544–553
Greenland S, Lash TL (2008) Bias analysis. In Modern Epidemiology, Rothman KJ, Greenland S, Lash TL (eds) 3rd edn, pp 345–380. Lippincott–Williams–Wilkins: Philadelphia
Hanley JA, McNeil BJ (1983) A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 148: 839–843
Hartge P, Whittemore AS, Itnyre J, McGowan L, Cramer D (1994) Rates and risks of ovarian cancer in subgroups of White women in the United States. Obstet Gynecol 84: 760–764
Imperiale T, Wagner D, Lin CY, Larkin GN, Rogge JD, Ransohoff DF (2000) Risk of advanced proximal neoplasms in asymptomatic adults according to the distal colorectal cancer findings. N Engl J Med 343: 169–174
Jakobsdottir J, Gorin MB, Conley YP, Ferrell RE, Weeks DE (2009) Interpretation of genetic association studies: markers with replicated highly significant odds ratios may be poor classifiers. PLoS Genet 5: 1–8. doi:10.1371/journal.pgen.1000337
Janssens AC, Aulchenko YS, Elefante S, Borsboom GJ, Steyerberg EW, van Duijn CM (2006) Predictive testing for complex diseases using multiple genes: fact or fiction? Genet Med 8: 395–400
Janssens AC, Moonesinghe R, Yang Q, Steyerberg EW, van Duijn CM, Khoury MJ (2007) The impact of genotype frequencies on the clinical validity of genomic profiling for predicting common chronic diseases. Genet Med 9: 528–535
Kraft P, Hunter DJ (2009) Genetic risk prediction – are we there yet? N Engl J Med 360: 1701–1703
Marshall RJ (2001) Displaying categorical data relationships by scaled rectangle diagrams. Stat Med 20: 1077–1088
Marshall RJ (2005) Scaled rectangle diagrams can be used to visualize clinical and epidemiological data. J Clin Epidemiol 58: 974–981
Marshall RJ (2009) Cardiovascular risk can be represented by scaled rectangle diagrams. J Clin Epidemiol 62: 998–1000
Miller DP, Neuberg D, de Vivo I, Wain JC, Lynch TJ, Su L, Christiani DC (2003) Smoking and the risk of lung cancer: susceptibility with GSTP1 polymorphisms. Epidemiology 14: 545–551
National Center for Health Statistics (2003) Worktable 210R. Death rates for 113 selected causes, alcohol-induced causes, drug-induced causes and injury by firearms, by 5-year age groups, race, and sex. http://www.cdc.gov/nchs/datawh/statab/unpubd/mortabs/gmwk210_10.htm. (Last accessed July 2006)
Parkin DM, Bray F, Ferlay J, Pisani P (2005) Global cancer statistics, 2002. CA Cancer J Clin 55: 74–108
Rockhill B, Byrne C, Rosner B, Louie MM, Colditz G (2003) Breast cancer risk prediction with a log-incidence model: evaluation of accuracy. J Clin Epidemiol 56: 856–861
Selvachandran SN, Hodder RJ, Ballal MS, Jones P, Cade D (2002) Prediction of colorectal cancer by a patient consultation questionnaire and scoring system: a prospective study. Lancet 360: 278–283
Spitz MR, Hong WK, Amos CI, Wu X, Schabath MB, Qiong D, Shete S, Etzel CJ (2007) A risk model for prediction of lung cancer. J Natl Cancer Inst 99: 715–726
Surveillance and End Results (SEER) (2005) Lung Cancer Incidence for Surveillance and End Results (SEER) – 2005. US National Institutes for Health. http://www.seer.cancer.gov. (Last accessed July 2006)
Tice JA, Cummings SR, Ziv E, Kerlikowske K (2005) Mammographic breast density and the Gail model for breast cancer risk prediction in a screening population. Breast Cancer Res Treat 94: 115–122
Tyrer J, Duffy SW, Cuzick J (2004) A breast cancer prediction model incorporating familial and personal risk factors. Stat Med 23: 1111–1130
Vickers AJ, Kramer BS, Baker SG (2006) Selecting patients for randomized trials: a systematic approach. Trials 7: 30.
Wang LI, Miller DP, Sai Y, Liu G, Su L, Wain JC, Lynch TJ, Christiani DC (2001) Manganese superoxide dismutase alanine-to-valine polymorphism at codon 16 and lung cancer risk. J Natl Cancer Inst 93: 1818–1821
Wu X, Lin J, Grossman HB, Huang M, Gu J, Etzel CJ, Amos CI, Dinney CP, Spitz MR (2007) Projecting individualized probabilities of developing bladder cancer in White individuals. J Clin Oncol 25: 4974–4981
Xu X, Kelsey KT, Wiencke JK, Wain JC, Christiani DC (1996) Cytochrome P450 CYP1A1 MspI polymorphism and lung cancer susceptibility. Cancer Epidemiol Biomarkers Prev 5: 687–692
Acknowledgements
Our research was supported by a cancer prevention fellowship funded by the National Cancer Institute grant K07CA093592, National Cancer Institute grants CA55769, CA123208, CA074386 the Flight Attendant Medical Research Institute, and funds mandated by the Texas State Legislature, Fiscal Year 2007. The Liverpool Lung Project was supported by a programme grant from the Roy Castle Lung Cancer Foundation and the modelling of the LLP Risk Model by CRUK.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Rights and permissions
From twelve months after its original publication, this work is licensed under the Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
D'Amelio, A., Cassidy, A., Asomaning, K. et al. Comparison of discriminatory power and accuracy of three lung cancer risk models. Br J Cancer 103, 423–429 (2010). https://doi.org/10.1038/sj.bjc.6605759
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/sj.bjc.6605759