Abstract
Most information in linkage analysis for quantitative traits comes from pairs of relatives that are phenotypically most discordant or concordant. Confounding this, within-family outliers from non-genetic causes may create false positives and negatives. We investigated the influence of within-family outliers empirically, using one of the largest genome-wide linkage scans for height. The subjects were drawn from Australian twin cohorts consisting of 8447 individuals in 2861 families, providing a total of 5815 possible pairs of siblings in sibships. A variance component linkage analysis was performed, either including or excluding the within-family outliers. Using the entire dataset, the largest LOD scores were on chromosome 15q (LOD 2.3) and 11q (1.5). Excluding within-family outliers increased the LOD score for most regions, but the LOD score on chromosome 15 decreased from 2.3 to 1.2, suggesting that the outliers may create false negatives and false positives, although rare alleles of large effect may also be an explanation. Several regions suggestive of linkage to height were found after removing the outliers, including 1q23.1 (2.0), 3q22.1 (1.9) and 5q32 (2.3). We conclude that the investigation of the effect of within-family outliers, which is usually neglected, should be a standard quality control measure in linkage analysis for complex traits and may reduce the noise for the search of common variants of modest effect size as well as help identify rare variants of large effect and clinical significance. We suggest that the effect of within-family outliers deserves further investigation via theoretical and simulation studies.
Similar content being viewed by others
Introduction
In linkage analysis for quantitative traits, extreme individuals provide a relatively large contribution to the test statistic. Indeed, this is the basis of selective genotyping to maximise power while minimising costs. For example, the EDAC design, in which extremely discordant pairs and concordant pairs of relatives are selected, has been proposed as a powerful design.1 If there are quantitative trait loci (QTL) of large effects segregating in pedigrees, then relatives that do not share alleles identical by descent (IBD) at the trait locus will tend to be phenotypically dissimilar, and relatives that share one or two alleles IBD at the trait locus will tend to be phenotypically similar. This relationship between IBD status and phenotypic similarity forms the basis of QTL mapping in human populations.2, 3
The corollary of the advantage of relatives with extreme phenotypes for QTL mapping is that large differences in phenotypes within families (ie, within-family outliers) can have a large effect on the test statistic for linkage, even if the individual phenotypes are not obvious outliers in the entire sample. Within-family outliers may obscure a real linkage signal or create a false positive one. However, in practice it is usually not known if a within-family outlier arises because of genetic or environmental (eg, measurement error or perinatal trauma) factors. Herein lies the dilemma of how to deal with within-family outliers: under the null hypothesis of no linkage they can create false positives, yet they would be expected under the alternative hypothesis of segregating alleles of large effects. The existence of rare alleles with large effects would require large sample sizes for detection and replication and would obscure the linkage signal at other loci contributing to normal variation. On the other hand, rare alleles of large effect size may be a major contributor to the caseload of clinical geneticists and may point to important pathways in the genetic regulation of a phenotype of interest.
Height is one of the most important anthropometric measures. It has been suggested as an indicator of childhood living conditions4 and has been associated with the risk of coronary heart diseases,5 intelligence,6 educational attainment,7 longevity8 and social mobility.9 Height is also an excellent model trait for studying the genetic architecture of complex quantitative traits.10 It is a normally distributed quantitative trait and highly heritable. A wide variety of genetic designs all converge on a heritability for height of about 0.8.10, 11
To date, numerous QTL for height have been mapped to almost all chromosomes (see Supplementary Table). With the exception of a few regions from a small number of studies, most of them have been mapped with only moderate statistical support (ie, LOD score <3), which is similar to that seen for many complex traits. This suggests that most of the genes influencing height have small to moderate effects. To be able to detect QTL with small to moderate effects, a large sample size is required.12 Therefore, using a large sample size of 8447 individuals from 2861 families of twins, our study aimed: (1) to detect chromosomal regions influencing height, including those with smaller effect sizes that may be missed by studies using smaller samples; (2) to replicate previously reported chromosomal regions affecting height; and (3) to empirically investigate the effect of within-family outliers on the evidence for linkage.
Subjects and methods
The study was approved by the Human Research Ethics Committee of the Queensland Institute of Medical Research and all participants gave their signed informed consent.
Subjects
The subjects were drawn from two cohorts, an adolescent and an adult cohort. The younger cohort constituted adolescent twins and their siblings who participated in various studies conducted at the Genetic Epidemiology Laboratory of the Queensland Institute of Medical Research, Australia. Height for these individuals was measured by a nurse using a stadiometer at the age of 12 and 14 as part of a melanoma risk factors study13 and at the age of 16 for a study on cognition.14 From these adolescents, we chose the measurement at the age of 16, which was available on 1575 individuals.
The adult cohort constituted twins and their families (eg, parents and other family relationships) who had been drawn from the Australian Twin Registry for various studies, including asthma and allergy,15 anxiety and depression,16 alcoholism17 and factors for cardiovascular disease.18 From the adult cohort, clinical measurement and/or self-reported height were available from 36 427 individuals and more than one measurement was available for some individuals due to their participation in multiple studies. Following Cornes et al,19 rules were implemented to select the most accurate measurement for further analysis. Briefly, if a clinical measurement was available for an individual, it was used for the analysis. Out of 36 427 individuals, clinical measurements were available for 5129 individuals (14.1%). If there was more than one measurement, the most recent measurement was chosen subject to consistency checks (see Supplementary Figure).
Genotyping
Microsatellite marker genotypes were available from several genome-wide and fine mapping studies. A detailed description of genotyping, cleaning and merging of each of the smaller genome scans has been provided by Zhu et al13 for the adolescent cohort and by Cornes et al19 for the adult cohort. Further genotypic data from a subset of individuals previously described by Cornes et al19 and 4575 newly genotyped individuals from the adult cohort have been incorporated into the present study using the same procedures described by Cornes et al19 (M Luciano, G Zhu, KM Kirk, SD Gordon, AC Heath, GW Montgomery and NG Martin, personal communication).
Briefly, the procedure of cleaning and merging the smaller genome scans into a combined genome scan can be described as follows. Firstly, raw data from each genome scan were integrated into one combined genome scan. Some individuals were genotyped using the same markers in different genome scans. Collapsing these duplicate markers into one unique marker was not an option since the same markers from different genome scans were often genotyped using different primers, allele calling algorithms and measurement technologies. Thus, these markers were given unique identifiers and their map positions were separated by 0.001 cM to avoid zero-spacing. Secondly, if Mendelian inheritance errors were detected, all genotypes for that marker for a given family were removed by utilising the algorithm developed by O'Connell and Weeks.20 Finally, unlikely chromosomal recombination patterns were detected and removed using the –error option in the Merlin package.21 Based on the genotype data, the pedigree relationships between individuals were checked using standard relationship checking software, RELPAIR 2.0.122 and GRR.23
Subjects with phenotypic and genotypic data
Data from the two cohorts were combined, giving a total of 38 002 individuals. From these, only 9464 individuals have both phenotypic and genotypic data. Figure 1 show that subjects younger than 16 years old were mostly in their adolescent growth stage, so to minimise the heterogeneity of the phenotypic definition while maximising the sample size (ie, 846 subjects aged between 16 and 18 years old), only subjects ≥16 years of age were included in the analyses. Subjects were also selected if they were genotyped with more than 210 autosomal markers (the minimum number of autosomal markers from the smallest genome scan). In addition to that, 12 outliers (subjects with standardised height after sex and age adjustments of more than 4 SD above or below the mean) were removed. After the exclusions, the final sample of 8447 individuals was included in linkage analyses and its descriptive statistics is presented Table 1. This sample consisted of 2861 families, 5815 possible pairs of siblings in sibships (980, 2065 and 2770 pairs for male–male, female–female and opposite-sex pairs were, respectively) 3913 parent–offspring, 63 half-sibs, 8 cousins, 10 grandparent–grandchild and 146 avuncular relationships. In addition to DZ twin pairs and additional siblings, there were 236 MZ twin pairs. In the above calculation of the number of informative relative pairs, only one individual from an MZ pair was included.
Definition and removal of within-family outliers
In a family consisting of sibling pairs, let y1 and y2 be the phenotypic (residual) values of sibling 1 and sibling 2, respectively. Their phenotypic difference is D=y1−y2. By assuming that the phenotypic values are bivariate normally distributed with correlation coefficient r and σ the SD of y1 and y2, the expected mean and variance of square of D (D2) can be calculated using χ2 theory, D2∼[2(1−r)σ2]χ2(1). The mean of D2 is 2(1−r)σ2 and its variance is 8(1−r)2σ4 (see also Sham and Purcell24). Hence, the expected SD of D2 is 2√2(1−r)σ2.
Within-family outliers were defined as sibling pairs for which the squared phenotypic difference is much larger than expected from the population correlation. From our data, sibling correlation and residual SD (after a general linear model correction for the effects of age and sex) were 0.43 and 6.7 cm, respectively, so that the mean and SD of D2 are 51.2 and 72.4 cm, respectively. Thus, sibling pairs for which the squared phenotypic difference was 4 SD above the mean (ie, >341 cm2), which corresponds to an absolute difference 18.5 cm or greater, were categorised as within family outliers. There were 81 possible pairs of siblings in sibships with D2>4 SD above the mean. If within-family outliers were detected in families with more than two siblings, then not all individuals in a pair were removed, but only the individuals most responsible for the within-family outliers, that is, the individual with the largest deviation from the population mean. In total, 59 individuals were removed (0.7% of the total sample), which resulted in a reduction of 142 possible pairs of siblings in sibships, or 2.4% of the total number of possible pairs of siblings in sibships.
Power calculations
To assess the power of the present study to detect a QTL influencing the normal variation in height, a series of power calculations based on Sham et al,25 was performed using a genetic power calculator26 under the following assumptions: (1) an additive QTL is influencing the variation of height; (2) recombination rate between the marker and the QTL is 0; (3) a heritability of 0.8; (4) type 1 error rate (α)=4.8 × 10−5 (equivalent to a LOD score of 3.3). The expected LOD score was also calculated using the above assumptions as E(LOD)=(1+NCP)/4.605, with NCP the QTL non-centrality parameter.25
Linkage analysis
To identify and map chromosomal regions (QTL) influencing variation in height, a multipoint variance component linkage analysis was performed as implemented in the Merlin 1.0.1 (for autosomes) and MINX (for the X chromosome).21 As the framework for mapping the QTL, that is, establishing the position and order of the markers in the chromosomes, a locally weighted linear regression map (http://www.qimr.edu.au/davidD) based on NCBI Build 35.1 physical map positions, deCODE and Marshfield maps was used.27
Linkage analysis correlates the phenotypic similarity of relative pairs with their genotypic similarity (represented by the proportion of alleles shared identical by descent (IBD) at a specific position in the genome) (eg, Almasy and Blangero28). In a variance component framework, the observed variance is partitioned into components due to QTL effects (shared when pairs are IBD at a marker), polygenic effects (shared according to their genetic relationship) and environmental (non-shared) effects, using the observed covariance between relatives and IBD sharing at marker loci. The presence of a QTL at a specific chromosomal location was tested by comparing the likelihood that the QTL variance is zero (H0) with the likelihood that the QTL variance is different from zero (H1). The LOD score is defined as twice the difference between the log10 likelihood (H0) and (H1) (eg, Almasy and Blangero28). As suggested by Lander and Kruglyak,29 the present study considered LOD scores of 3.3 and 1.9 as significant and suggestive evidence of linkage between QTL and markers at the test position, respectively. The effects of within family outliers on linkage results were empirically examined by conducting linkage analyses on the data before and after removing individuals who were classified as within family outliers.
Results
Descriptive statistics
The mean height of males was larger than that of females with an estimated difference of 14.16 cm (SE 0.15). The regression slope of the age on height was −0.05 (SE 0.01) cm/year indicating gradual shortening of our aging sample, possibly confounded with a secular trend of increasing height in later birth cohort.30 Skewness and kurtosis values of the standardised residuals of height after a general linear model adjustment (in SPSS package) for the effects of age and sex were very close to zero (ie, skewness: 0.10 (SE 0.06); kurtosis: 0.03 (0.06). This is a good indication that our data have close to a normal distribution, which is an assumption of variance component linkage analysis by maximum likelihood and justifies use of asymptotic significance values for linkage.29 The average numbers of markers genotyped per individual was 542 (range, 211–1640). Overall, these numbers provided an average spacing of about 5 cM across the genome. The estimated sib correlations before and after removing within-family outliers were 0.43 and 0.48. The corresponding estimates of heritability were 0.83 and 0.84, respectively. The estimates of heritability were not identical to twice the sib correlations because they were estimated using all pedigree relationships, including parent–offspring and MZ pairs.
Detection of within-family outliers
In Figure 2 the distribution of the squared difference in phenotype between siblings (D2) is shown for all sibling pairs after removal of the effects of age and sex. The empirical mean and SD of D2 are 51.2 and 81.4 cm, respectively, whereas their predictions from χ2 theory (see Subjects and methods) are 51.2 and 72.4. Clearly there are a number of outlier pairs (ie, 81 pairs). The largest squared difference was 1000 cm2, corresponding to an absolute difference of 32 cm. For a trait such as height with a high heritability (and sibling correlation), such within-family deviations are not expected from genetic segregation of common variants of small effect, and removing these outliers appears justified.
A closer inspection to the outliers showed that there was no significant difference between the proportion of subjects with clinically measured and subjects with self-reported height in the outlying subjects and the rest of the sample (P-value=0.95). The proportion of same-sex and opposite-sex pairs in the outlying subjects and the rest of the samples was also not significantly different (P-value=0.23). The outlying subjects appear to be evenly distributed across tall and short stature and across age, but with fewer outliers after the age of 50. Most of the outlier pairs have similar age. The age correlation between sibling 1 and sibling 2 was 0.81. For three outlier pairs (six individuals) who were ∼16 at the time of measurement and between 21–28 years of age at the time of analyses, we checked the original recorded phenotype and telephoned those individuals about their current height. We found that the data in our database was consistent with both the initial records and that of the currently reported height difference.
Power calculations
The power of our sample to detect a QTL responsible for 5, 10 and 15% of the phenotypic variation at type 1 error rate (α) of 4.8. × 10−5 is 1, 32 and 89%, respectively. For a power of 80%, the required sample size to detect a QTL explaining 10% of the phenotypic variation is about 10 910 sib pairs. The expected LOD scores for a QTL explaining 5, 10 and 15% of the phenotypic variance are 0.9, 2.8 and 6.0, respectively.
Linkage analyses
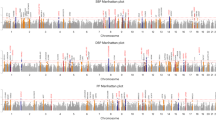
The multipoint LOD score profiles from linkage analyses including and excluding within-family outliers are presented in Figure 3 and the chromosomal regions that reached a LOD score of 1.5 or greater are presented in Table 2. The results showed that by excluding the outliers, the LOD scores increased for most regions, except for the peak on chromosome 15 (LOD score decreased from 2.3 to 1.2). When within-family outliers were excluded, 3 chromosomal regions (1q23.1 (LOD 2.0), 3q22.1 (1.9) and 5q32 (2.3)) were suggestive for linkage with height.
We have also performed additional linkage analyses where only subjects older than 18 or 20 years old were included in the analyses and the results were very similar (results not shown). In addition, the application of a regression method (implemented in the computer program Merlin-Regress21), which uses a linear combination of squared sums and squared difference as a dependent variable31 did not change the linkage results (results not shown).
Discussion
Genetic studies of normal variation in height are medically important and useful for understanding the genetic architecture of complex traits. Our genome-wide linkage analysis using a sample of 5815 possible pairs of siblings in sibships provides further evidence for the polygenic nature of height. Several chromosomal regions showed moderate linkage and three of them (1q23.1 (LOD 2.0), 3q22.1 (1.9) and 5q32 (2.3)) reached the asymptotic suggestive level of 1.9. However, despite our large sample, none of them reached the asymptotic threshold of 3.3 indicating significant linkage. Power calculations indicated that if there was a QTL explaining 15% or more of the variation in height segregating in our sample and the QTL was completely linked to the marker, it was unlikely to be missed since we had 89% power to detect it. Our results therefore suggest that normal variation in height is influenced by several or many genes with small-to-modest effect size.
Previous studies have identified several chromosomal regions showing significant linkage (ie, LOD score ≥3.3) with height (Supplementary Table). These included the regions on chromosome 1p21 (for males only),32 6q25.3,33 7q35,33 9q2234 12q13.1,33 13q33.1,33 14q23.1,35 and the X chromosome (Xp22 and Xq24).34 Many other studies have also supported these regions as being associated with height, including the regions on chromosome 1;35 chromosome 6;36 chromosome 7;37 chromosome 9;36 chromosome 12;32, 36, 38 and chromosome 14.39 Among these regions, 12q13.1 was replicated in this study with a LOD score of 1.4. The chromosomal regions of 3q22.1 and 5q32, which showed suggestive linkage in our study, have been previously mapped into a similar location. Using a combined population of 6752 individuals, Wu et al35 reported that 3q23 and 5q31.1 were suggestive for linkage with height (LOD=2.0 for both). Deng et al36 have also suggested that the region on chromosome 5 was associated with height. Although these regions are not exactly the same, the one LOD drop-off confidence intervals overlap.
Among many genes that have been associated with height, the vitamin D receptor (VDR) has recently received much attention. As one of the intracellular hormone receptors, the main role of VDR is to bind the active form of vitamin D. This gene has been mapped to 12q12–q1440 and it has been associated with height (eg,38, 41). Furthermore, a meta-analysis of published linkage studies on chromosome 12 has shown that there is significant evidence for the presence of a QTL on this chromosome.38 In the present study, the LOD score for this region did not reach suggestive linkage, but a LOD score of 1.4 was observed. Power calculations suggest that the expected LOD scores for a QTL explaining 5 to 10% of the phenotypic variance are 0.9 and 2.8, respectively, so if the VDR has a moderate effect on height, the observed LOD scores in this region are not inconsistent with VDR being a candidate gene for height. Other interesting genes that are located under or close to the linkage peaks were ADIPOR1 (1q32.1), PTHR1 (3p21.3), BCHE (3q26.1) and CYP19 (15q21.2) and MARFAN (15q21.1) (Figures 3). Variants in these genes have been associated with height.42, 43, 44, 45, 46
Linkage analysis was performed by excluding individuals who were categorised as within-family outliers. Within families, these individuals were regarded as discordant for height when the absolute difference of the height measure of siblings was more than 18.5 cm. Risch and Zhang1 have shown that selecting extremely discordant and concordant sib pairs is more powerful for linkage analysis than selecting random pairs. Thus, our strategy would seem to be counter productive because we removed the most extremely discordant pairs, hence the most informative pairs. However, by removing these outliers, their disproportionate contribution to the test statistic for linkage, which could be due to measurement errors or environmental effects, can be avoided. Extremely discordant pairs of siblings, who do not share any alleles IBD at a particular region in the genome, contribute strong apparent evidence for linkage. It is questionable to rely strongly on such pairs, because it is the absence of sharing that suggests linkage. The influence of a single pair of within-family outlier can be substantial. Across a number of studies we have noted that a single pair can change the LOD score by 0.5–1.0, and this occurs at many locations in the genome. On the other hand, one cannot discount the possibility of rare variants of large effect size producing ‘outlier’ effects. Replication of these in other studies might help to reveal variants of clinical significance in some rare families, even if unimportant at the population level. Ultimately it is the researcher who has to make a judgement about the validity of data to be used for analysis, but we urge investigators to be critical regarding within-family outliers.
When we followed up a number of individuals who were responsible for within-family outliers we found no evidence for measurement or database entry errors. This leaves open the interesting question whether the large observed differences within families are caused by unknown environmental factors of large effects, for example, in utero environmental insults, childhood disease and epigenetic effects or caused by rare alleles of large effect. Linkage analysis on collections of small nuclear families, as employed in our study, or in the case of disease collections of affected sibling pairs, are not suitable to detect segregating rare variants of large effect that do not explain a substantial (say, >5%) of genetic variance in the population. Moreover, the existence of such variants may obscure the detection of loci that do explain significant variation in the population because of the disproportionate contribution of within-family outliers to the LOD score. The identification of large pedigrees with multiple within-pedigree ‘outliers’ is the most efficient approach to map rare alleles of large effect.
We also noted that besides extreme discordant pairs, linkage information comes also from concordant pairs. Mean-corrected squared sum (S)47 was used to identify pairs that are phenotypically similar, that is, pairs of sibs that both are extremely short or extremely tall. From our data, the mean and SD of S are 129.4 and 180.0, respectively. These agree very well with the expected mean [2(1+r)σ2] and SD [2√2(1+r)σ2]. However, as shown by Visscher and Hopper,48 most of the information on linkage comes from the squared difference (rather than the squared sum) of the phenotypes of a pair of siblings. Therefore, we did not remove these extremely concordant pairs in our analysis.
In linkage analyses, we also excluded 12 extreme individuals (≥4 SD below or above the mean). From these individual outliers, there are 34 possible pairs of siblings in sibships. Within family, some of these individual outliers are also likely to be extreme compared to their siblings, which thus can be categorised as within family outliers. Therefore, it is difficult to disentangle the effect of within-family outliers and individual outliers per se. Individual outliers that are not informative for linkage are unlikely to have an effect on the test statistic for linkage, whereas individual outliers that are informative (eg, have siblings with phenotypes and genotypes) are likely to have an effect by creating within-family discordant pairs.
In conclusion, a genome-wide linkage analysis has revealed three chromosomal regions [1q23.1 (LOD 2.0), 3q22.1 (1.9) and 5q32 (2.3)] suggestive for linkage with height in a large sample of Australian twin families. Despite a large sample size, the moderate statistical support for most of the identified chromosomal regions suggests that height is influenced by several or many genes, each having a modest effect. We also confirmed the disproportionate influence of within-family outliers to the linkage results. While the precise effects of these outliers on linkage results cannot be quantified without theoretical or simulation studies, our findings showed that the disproportionate contribution of a small number of outlier pairs, which could be due to environmental effects or measurement errors, can make a big difference to linkage results. Therefore, we recommend that researchers (re)examine their linkage scans for such outliers as part of routine quality control and robustness analysis. Such outliers can distort the search for common variants of modest effect size, but may also help identify rare variants of large effect and clinical significance. We suggest that the effect of within-family outliers deserves further investigation via theoretical and simulation studies.
References
Risch N, Zhang H : Extreme discordant sib pairs for mapping quantitative trait loci in humans. Science 1995; 268: 1584–1589.
George AW, Visscher PM, Haley CS : Mapping quantitative trait loci in complex pedigrees: a two-step variance component approach. Genetics 2000; 156: 2081–2092.
Haseman JK, Elston RC : The investigation of linkage between a quantitative trait loci and a marker locus. Behav Genet 1972; 2: 3–19.
Peck MN, Lundberg O : Short stature as an effect of economic and social conditions in childhood. Soc Sci Med 1995; 41: 733–738.
McCarron P, Okasha M, McEwen J, Smith GD : Height in young adulthood and risk of death from cardiorespiratory disease: a prospective study of male former students of Glasgow University, Scotland. Am J Epidemiol 2002; 155: 683–687.
Abbott RD, White LR, Ross GW et al: Height as a marker of childhood development and late-life cognitive function: the Honolulu-Asia Aging Study. Pediatrics 1998; 102: 602–609.
Silventoinen K, Krueger RF, Bouchard TJ, Kaprio J, McGue M : Heritability of body height and educational attainment in an international context: comparison of adult twins in Minnesota and Finland. Am J Hum Biol 2004; 16: 544–555.
Samaras TT, Elrick H, Storms LH : Is height related to longevity? Life Sci 2003; 72: 1781–1802.
Cernerud L : Height and social mobility. A study of the height of 10 year olds in relation to socio-economic background and type of formal schooling. Scand J Soc Med 1995; 23: 28–31.
Visscher PM, Medland SE, Ferreira MAR et al: Assumption-free estimation of heritability from genome-wide identity-by-descent sharing between full siblings. PLoS Genet 2006; 2: 316–325.
Silventoinen K : Determinants of variation in adult body height. J Biosoc Sci 2003; 35: 263–285.
Risch N, Merikangas K : The future of genetic studies of complex human diseases. Science 1996; 273: 1516–1517.
Zhu G, Evans DM, Duffy DL et al: A genome scan for eye color in 502 twin families: most variation is due to a QTL on chromosome 15q. Twin Res 2004; 7: 197–210.
Wright MJ, Martin NG : Brisbane Adolescent Twin Study: outline of study methods and research projects. Aust J Psychol 2004; 56: 65–78.
Duffy DL, Mitchell CA, Martin NG : Genetic and environmental risk factors for asthma. Am J Respir Crit Care Med 1998; 157: 840–845.
Wray NR, James MR, Mah SP et al: Anxiety and comorbid measures associated with PLXNA2. Arch Gen Psychiatry 2007; 64: 318–326.
Morley KI, Medland SE, Ferreira MA et al: A possible smoking susceptibility locus on chromosome 11p12: evidence from sex-limitation linkage analyses in a sample of Australian twin families. Behav Genet 2006; 36: 87–99.
Beekman M, Heijmans BT, Martin NG et al: Evidence for a QTL on chromosome 19 influencing LDL cholesterol levels in the general population. Eur J Hum Genet 2003; 11: 845–850.
Cornes BK, Medland SE, Ferreira MAR et al: Sex-limited genome-wide linkage scan for body mass index in unselected sample of 933 Australian twin families. Twin Res Hum Genet 2005; 8: 612–632.
O'Connell JR, Weeks DE : An optimal algorithm for automatic genotype elimination. Am J Hum Genet 1999; 65: 1733–1740.
Abecasis GR, Cherny SS, Cookson WO, Cardon LR : Merlin-rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet 2002; 30: 97–101.
Epstein MP, Duren WL, Boehnke M : Improved inference of relationship for pairs of individuals. Am J Hum Genet 2000; 67: 1219–1231.
Abecasis GR, Cherny SS, Cookson WO, Cardon LR : GRR: graphical representation of relationship errors. Bioinformatics 2001; 17: 742–743.
Sham PC, Purcell S : Equivalence between Haseman–Elston and variance–components linkage analyses for sib pairs. Am J Hum Genet 2001; 68: 1527–1532.
Sham PC, Cherny SS, Purcell S, Hewitt JK : Power of linkage versus association analysis of quantitative traits, by use of variance-components models, for sibship data. Am J Hum Genet 2000; 66: 1616–1630.
Purcell S, Cherny SS, Sham PC : Genetic Power Calculator: design of linkage and association genetic mapping studies of complex traits. Bioinformatics 2003; 19: 149–150.
Duffy DL : An integrated genetic map for linkage analysis. Behav Genet 2006; 36: 4–6.
Almasy L, Blangero J : Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Hum Genet 1998; 62: 1198–1211.
Lander E, Kruglyak L : Genetic dissection of complex traits: guidelines for interpreting and reporting linkage results. Nat Genet 1995; 11: 241–247.
Macgregor S, Cornes BK, Martin NG, Visscher PM : Bias, precision and heritability of self-reported and clinically measured height in Australian twins. Hum Genet 2006; 120: 571–580.
Sham PC, Purcell S, Cherny SS, Abecasis GR : Powerful regression-based quantitative-trait linkage analysis of general pedigrees. Am J Hum Genet 2002; 71: 238–253.
Sammalisto S, Hiekkalinna T, Suviolahti E et al: A male-specific quantitative trait locus on 1p21 controlling human stature. J Med Genet 2005; 42: 932–939.
Hirschhorn JN, Lindgren CM, Daly MJ et al: Genomewide linkage analysis of stature in multiple populations reveals several regions with evidence of linkage to adult height. Am J Hum Genet 2001; 69: 106–116.
Liu Y-Z, Guo Y-F, Xiao P et al: Epistasis between loci on chromosomes 2 and 6 influences human height. J Clin Endocrinol Metab 2006; 119: 295–304.
Wu X, Cooper RS, Boerwinkle E et al: Combined analysis of genomewide scans for adult height: results from the NHLBI Family Blood Pressure Program. Eur J Hum Genet 2003; 11: 271–274.
Deng H-W, Xu F-H, Liu Y-Z et al: A whole-genome linkage scan suggests several genomic regions potentially containing QTLs underlying the variation of stature. Am J Med Genet 2002; 113: 29–39.
Perola M, Ohman M, Hiekkalinna T et al: Quantitative-trait-locus analysis of body-mass index and of stature, by combined analysis of genome scans of five Finnish Study Groups. Am J Hum Genet 2001; 69: 117–123.
Dempfle A, Wudy SA, Saar K et al: Evidence for involvement of the vitamin D receptor gene in idiopathic short stature via a genome-wide linkage study and subsequent association studies. Hum Mol Genet 2006; 15: 2772–2783.
Mukhopadhyay N, Weeks DE : Linkage analysis of adult height with parent-of-origin effects in the Framingham Heart Study. BMC Genet 2003; 4 (Suppl 1): S76.
Online Mendelian Inheritance in Man, OMIM (TM). Baltimore, MD: Johns Hopkins University, MIM Number: {*601769}:{1/25/2007}: accessed URL: http://www.ncbi.nlm.nih.gov/omim/
Lorentzon M, Lorentzon R, Nordstrom P : Vitamin D receptor gene polymorphism is associated with birth height, growth to adolescence, and adult stature in healthy Caucasian men: a cross-sectional and longitudinal study. J Clin Endocrinol Metab 2000; 85: 1666–1671.
Ellis JA, Stebbing M, Harrap SB : Significant population variation in adult male height associated with the Y chromosome and the aromatase gene. J Clin Endocrinol Metab 2001; 86: 4147–4150.
Scillitani A, Jang C, Wong BY-L, Hendy GN, Cole DEC : A functional polymorphism in the PTHR1 promoter region is associated with adult height and BMD measured at the femoral neck in a large cohort of young Caucasian women. Hum Genet 2006; 119: 416–421.
Siitonen N, Pulkkinen L, Mager U et al: Association of sequence variations in the gene encoding adiponectin receptor 1 (ADIPOR1) with body size and insulin levels. The Finnish Diabetes Prevention Study. Diabetologia 2006; 49: 1795–1805.
Souza RLR, Fadel-Picheth C, Allebrandt KV, Furtado L, Chautard-Freire-Maia EA : Possible influence of BCHE locus of butyrylcholinesterase on stature and body mass index. Am J Phys Anthropol 2005; 126: 329–334.
Mamada M, Yorifuji T, Yorifuji J et al: Fibrillin I gene polymorphism is associated with tall stature of normal individuals. Hum Genet 2007; 120: 733–735.
Drigalenko E : How sib pairs reveal linkage. Am J Hum Genet 1998; 63: 1242–1245.
Visscher PM, Hopper JL : Power of regression and maximum likelihood methods to map QTL from sib-pair and DZ twin data. Ann Hum Genet 2001; 65: 583–601.
Acknowledgements
We thank the twins and their families for their participation. For the ongoing data collection, recruitment and organisation of the studies in which the phenotypes were collected, we thank Marlene Grace and Ann Eldridge who collected the adolescent data; Dixie Statham who supervised collection of much of the adult data; Anjali Henders and Megan Campbell for managing sample processing; David Smyth, Scott Gordon and Harry Beeby for IT support. The genome scans of adolescents were supported by the Australian NHMRC's Program in Medical Genomics (NHMRC-219178) and a grant to Dr Jeff Trent from the Center for Inherited Disease Research at Johns Hopkins University. CIDR is fully funded through a federal contract from the National Institutes of Health to The Johns Hopkins University, Contract Number N01-HG-65403. For genome scans of adults, we acknowledge and thank the Mammalian Genotyping Service, Marshfield WI (Director: Dr James Weber) for genotyping under grants to Drs Daniel T O'Connor, David Duffy, Patrick Sullivan and Dale Nyholt; Drs Eline Slagboom, Bas Heijmans and Dorret Boomsma for the Leiden genome scan; Dr Peter Reed for the Gemini genome scan; and Dr Jeff Hall for the Sequana genome scan. This research was supported in part by Grants from NIAAA (USA) AA007535, AA013320, AA013326, AA014041, AA07728, AA10249, AA11998, the GenomEUtwin project, supported by the European Union contract number QLRT-2001-01254, and NHMRC (Australia) 941177, 951023, 950998, 981339, 241916, 941944 and 389892. We thank Jonathan Hansen, Allan McRae, Sarah Medland and Gu Zhu for discussions; Bill Hill and Sri Shekar for their comments on the earlier draft of the article. Beben Benyamin thanks the School of Biological Sciences, University of Edinburgh and the Overseas Research Student Award for providing his PhD scholarship.
Author information
Authors and Affiliations
Corresponding author
Additional information
Conflict of interest
None declared.
Supplementary Information accompanies the paper on European Journal of Human Genetics website (http://www.nature.com/ejhg)
Supplementary information
Rights and permissions
About this article
Cite this article
Benyamin, B., Perola, M., Cornes, B. et al. Within-family outliers: segregating alleles or environmental effects? A linkage analysis of height from 5815 sibling pairs. Eur J Hum Genet 16, 516–524 (2008). https://doi.org/10.1038/sj.ejhg.5201992
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/sj.ejhg.5201992